我很复杂,简介不了。|| 但你可以使用魔法上国际站看主页。
追踪最近的用户名外显变动记录。
最近的文章、讨论、云剪贴板与社区记录
在文章《高观点下的三角函数》发表评论:
三角函数的积分和用不用和差角公式没啥关系吧。教材里sinx求导一般就是和差化积然后等价无穷小证吧,不知道哪里能用和差角公式。
在文章《高观点下的三角函数》发表评论:
本文例题中的证法并不是最简洁的。事实上对于自变量是等差数列的正余弦函数求和,高中课内通常会介绍一种更为简单的方法,留作习题。
在文章《多元微分学(1)》发表评论:
没图qwq
## 定义 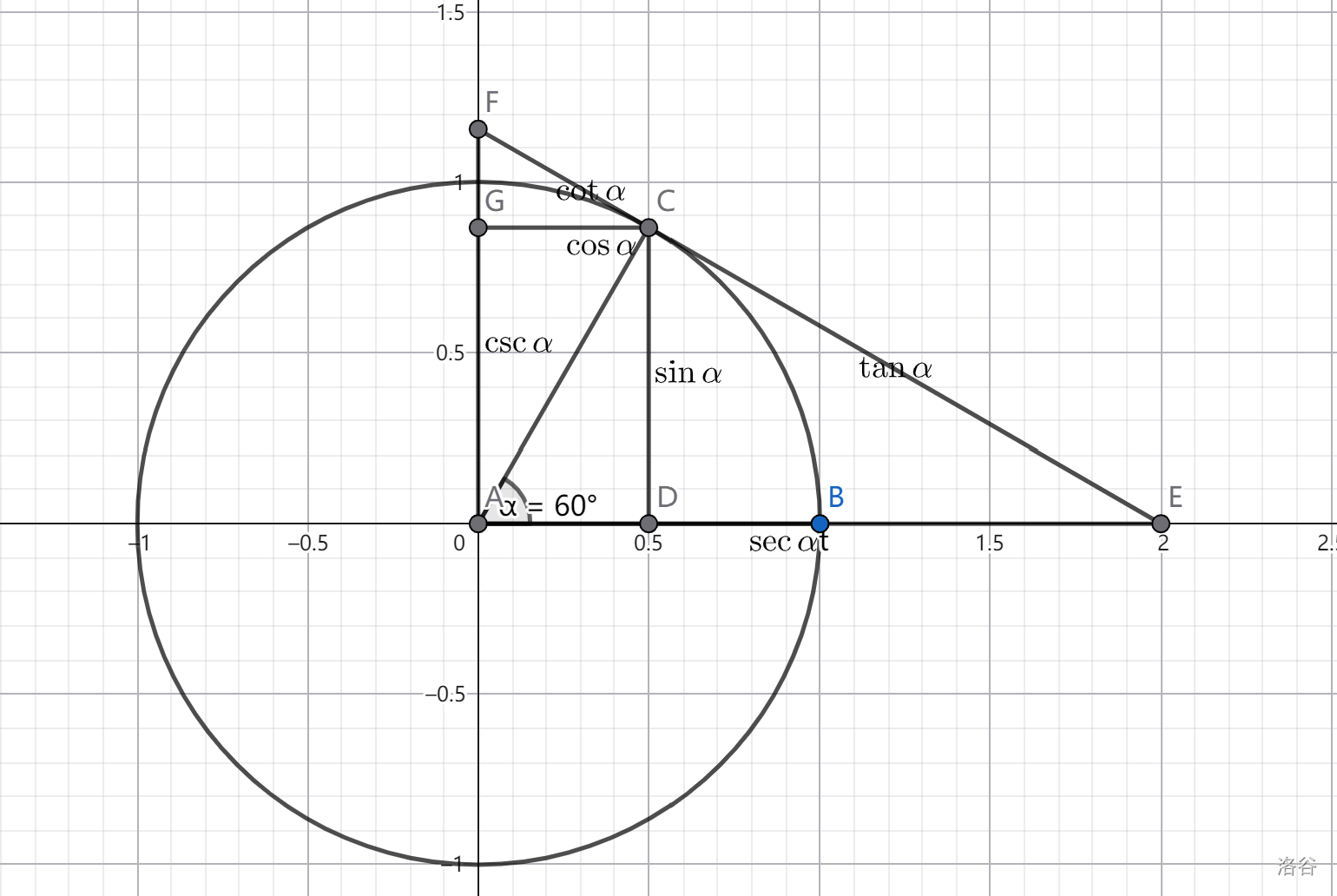 ## 从欧拉公式到三角函数 引入 $e^{i\theta}=\cos\theta+i\sin \theta$. 不妨两边同时取泰勒级数对比系数得证。 > 什么?你问我泰勒展开怎么证…
在文章《不是哥们你说话是人能说出来的吗?》发表评论:
知。不。路。反。是。是。代。 AI。
在文章《二项式定理的一个推广》发表评论:
还以为推广是指从生成函数理解莱布尼茨公式和二项式定理的共同点,怎么是这个。
> 考虑值域 $[1,m]$ 的 $n$ 项整数列 $\{a_n\}$,每次操作可以向交互库提出一个值域 $[1,m]$ 的 $n$ 项整数列 $\{b_n\}$,交互库会执行下述操作: > 1. $p_i=[a_i=b_i].$ > 2. $\forall i \in [1,m],i \in \mathbb{N}_+…
在讨论《求推荐圆锥曲线学习资料》回复:
@[Crescent_Rose_](luogu://user/232838) 怎么 at 错了qwq
在讨论《求推荐圆锥曲线学习资料》回复:
@[GUO120822](luogu://user/704562) 文章广场之前不是有一份高中数学笔记么,我觉得那份的圆锥曲线就还行。或者你也可以去知乎找找。
在文章《小粉兔你是一只香香软软的小蛋糕》发表评论:
小粉兔我错了!
> 听说文字越疯分越高。 小粉兔煎得外酥里嫩放在面前,奶香奶香的味道,丝滑的手感,软软的身体,真的好喜欢好喜欢。咬一口,身娇体软,入口即化,有一股红糖的甜味,香甜软糯,不会粘牙。 白!嫩!香!滑!摸一下!QQ弹弹,绵柔香软,滑滑嫩嫩酥酥脆脆,黏黏糊糊油油腻腻。 趴上去猛地吸一口!扑鼻诱人,色泽金黄,外酥里嫩,香气浓郁,…
在讨论《伪证了吗?》回复:
已严肃完成今日《孪生素数猜想的证明:基于 Deepsleep AI 大模型》大学习
在讨论《求FJ压缩包》回复:
破了踢我一下。@[duanjunhong001](luogu://user/543796)
在讨论《求FJ压缩包》回复:
自己找人拿一份考场代码,然后学一下 [这个](https://zhuanlan.zhihu.com/p/688497770)。
在讨论《关于钩子》回复:
@[pbds_](luogu://user/1820333)
在讨论《关于钩子》回复:
钩6稳 钩7功德检定
在讨论《求估 6 钩线》回复:
@[Gavinzhou](luogu://user/1320771)@[shellyang2023](luogu://user/1032105)@[_O_v_O_](luogu://user/782941)@[clo201111](luogu://user/1123752)@[SleepWithMiku](luogu:…
如题,惊奇地发现往年你谷水友估线普遍偏高。若考虑如上因素,6 钩线大概多少? 以及 FJ 一等线大概多少? 另外也可以给你认为的可能上限。 你 **不需要** 为你的言论负责,所以大胆给谢谢你。 另:有没有人组织估线大赛之类的游戏,在代码公示前比谁估得更准之类的。
在讨论《求一个客观评价CSP- S的(^ー゜)》回复:
@[DHeasy](luogu://user/528325)
在讨论《T1以下算法对不对》回复:
@[Literally](luogu://user/638141) 我也慌。所以啥是一个人不能换两次。
在讨论《【悬关】最密堆积问题》回复:
@[Infter](luogu://user/386547) 不是的。比如说二维超球其实是圆,二维超平面其实是边,用尽可能少的边围成的封闭图形,其实就是三角形,因此二维情况下是在一个三角形里堆积圆。 同理,三维情况下就是在正四面体里堆球。 希望扩展到 $n$ 维情况下。 对不起之前把铃给按掉了没看见/wul 浅诈个尸(…
在讨论《关于点格棋》回复:
@[__Silvefish__](luogu://user/570352) 诈个尸。一般正规棋盘都是 $n \times n$ 的,已经穷举证明 $n \le 3$ 都是后手必胜,我相信也许都是后手必胜的吧。 我听说有论文讲了这个的,但是没去找,您感兴趣的话可以搜一下。 我估计就算有必胜策略也是类似于五子棋的情况,就是…
在一张 $n \times m$ 的网格图中(指格子有 $n \times m$ 个),蓝方和红方轮流操作,蓝方先手。 * 每次操作选择一个格子的一条边涂上自己的颜色。 * 如果这条边是某个格子的最后一条未涂色的边(不论其它边是什么颜色),那么对于每个这样的格子,都涂上自己的颜色。 * 如果一次操作后至少有一个格子被涂…
在讨论《求助一个数学问题》回复:
@[TimSwn090306](luogu://user/564732) 是不是我没描述清楚?就是说当 $n$ 足够大的时候,由于“公比”极限是 $\frac{\sqrt{5}-1}{2}$,也就是存在近似的公比,所以如果下标不等差就一定不成等比。然而 $n$ 不够大的时候没有“公比”,所以只能人工验证。四色定理也是这…
在讨论《求助一个数学问题》回复:
注意到 $F_n^2-F_{n-k}F_{n+k}=(-1)^{n-k}F_k^2 \not = 0$,可以直接代通项公式证如上结论。 由此,若下标等差则必不成等比。而 $\lim_{n \to +\infin} \frac{F_{n+1}}{F_n}=\frac{\sqrt{5}-1}{2}$,所以可以写份代码验证数…