专栏文章

高观点下的三角函数

xxixihaha2021
学习·文化课参与者 7已保存评论 8

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
8 条
当前快照
1 份
快照标识符
@mll50co1
此快照首次捕获于
2026/02/14 01:04
6 天前
此快照最后确认于
2026/02/19 01:01
14 小时前
查看原文

定义

从欧拉公式到三角函数

引入 eiθ=cos⁡θ+isin⁡θe^{i\theta}=\cos\theta+i\sin \theta.
不妨两边同时取泰勒级数对比系数得证。
什么？你问我泰勒展开怎么证？不妨猜测原函数与一个多项式函数的差是高阶小量，然后依次积分得到系数。进而利用极限证明余项更高阶，从而猜想正确。
  • 恒等式
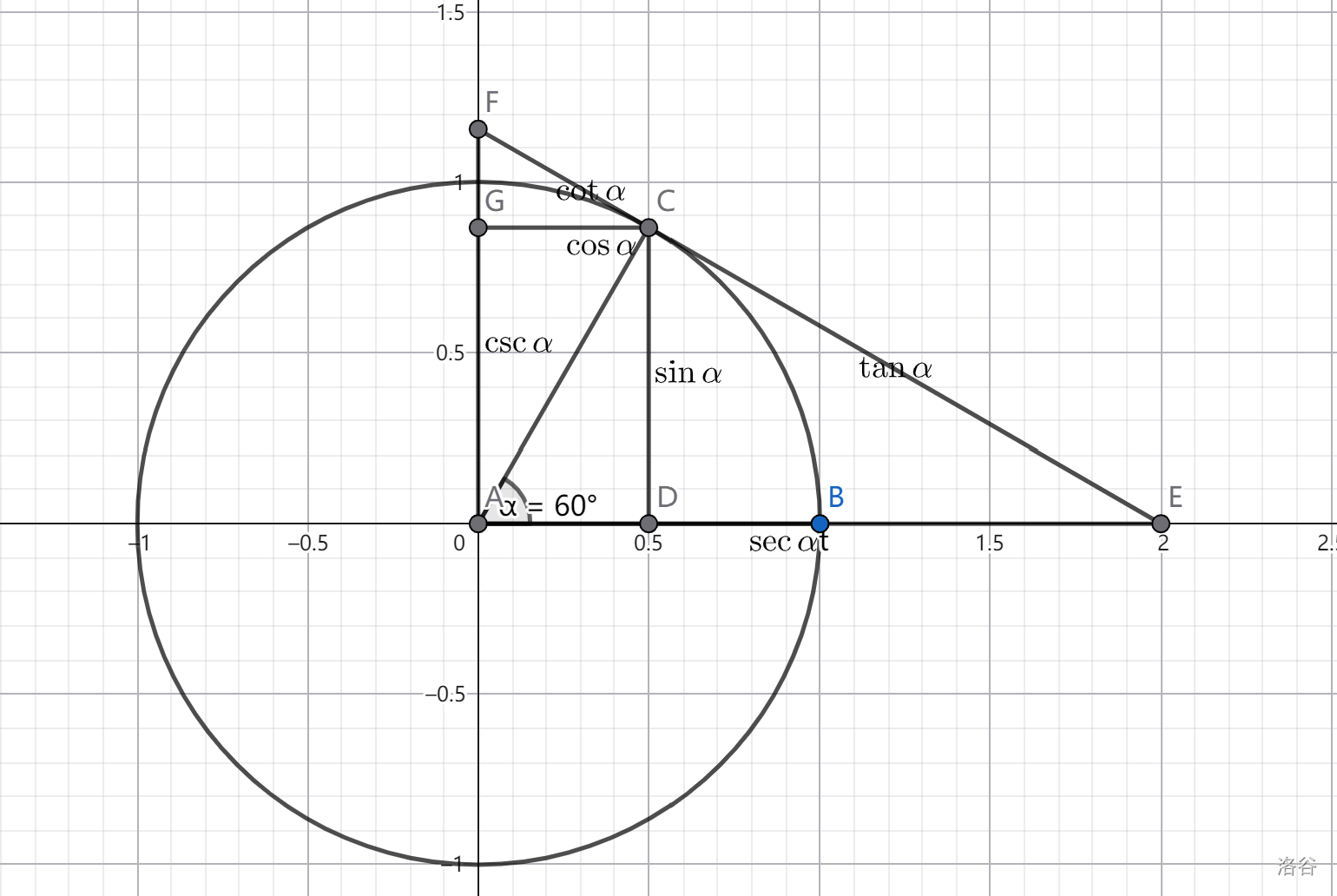
{eiθ=cos⁡θ+isin⁡θ,e−iθ=cos⁡θ−isin⁡θ.  ⟹  {eiθe−iθ=cos⁡2θ+sin⁡2θ=1,sin⁡θ=eiθ−e−iθ2i,cos⁡θ=eiθ+e−iθ2.\begin{aligned} \begin{cases} e^{i\theta}=\cos\theta+i\sin\theta, \\ e^{-i\theta}=\cos\theta-i\sin\theta. \end{cases} \\ \implies \begin{cases} e^{i\theta}e^{-i\theta}=\cos^2\theta+\sin^2\theta=1, \\ \sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i},\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}. \end{cases} \end{aligned}
  • 和角公式
cos⁡(α+β)+isin⁡(α+β)=ei(α+β)=eiαeiβ=(cos⁡α+isin⁡α)(cos⁡β+isin⁡β)=(cos⁡αcos⁡β−sin⁡αsin⁡β)+i(sin⁡αsin⁡β+cos⁡αsin⁡β).\begin{aligned} \cos(\alpha+\beta)+i\sin(\alpha+\beta)&=e^{i(\alpha+\beta)} \\ &=e^{i\alpha}e^{i\beta} \\ &=(\cos\alpha+i\sin\alpha)(\cos\beta+i\sin\beta) \\ &=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)+i(\sin\alpha\sin\beta+\cos\alpha\sin\beta). \end{aligned}
  • 倍角公式
cos⁡kθ+isin⁡kθ=ekiθ=(eiθ)k=(cos⁡θ+isin⁡θ)k=∑j=0kij(kj)cos⁡k−jθsin⁡jθ=(∑j=0[k2](−1)j(k2j)cos⁡k−2jθsin⁡2jθ)+i(∑j=0[k−12](−1)j(k2j+1)cos⁡k−2j−1θsin⁡2j+1θ).\begin{aligned} \cos k\theta+i\sin k\theta &= e^{ki\theta} \\ &= (e^{i\theta})^k \\ &= (\cos\theta+i\sin\theta)^k \\ &= \sum_{j=0}^k i^j\binom{k}{j}\cos^{k-j}\theta\sin^j\theta \\ &= (\sum_{j=0}^{[\frac{k}{2}]}(-1)^j\binom{k}{2j}\cos^{k-2j}\theta\sin^{2j}\theta)+i(\sum_{j=0}^{[\frac{k-1}{2}]}(-1)^j\binom{k}{2j+1}\cos^{k-2j-1}\theta\sin^{2j+1}\theta). \end{aligned}
也可以利用上述多项式（结合 sin⁡2θ+cos⁡2θ=1\sin^2\theta+\cos^2\theta=1）反解出 cos⁡θ\cos\theta 或 sin⁡θ\sin\theta，从而解决 k∈Qk \in \mathbb{Q} 时的问题。
  • 例：
∑k=0ncos⁡kθ(θ≠2kπ,k∈Z)=∑k=0nRe(ekiθ)=Re(∑k=0nekiθ)=Re(∑k=0n(eiθ)k)=Re(1−(eiθ)n+11−eiθ)=Re(e(n+1)iθ−1eiθ−1)=Re(e12(n+1)iθ(e12(n+1)iθ−e−12(n+1)iθ)e12iθ(e12iθ−e−12iθ))=Re(e12(n+1)iθ2isin⁡(12(n+1)θ)e12iθ2isin⁡(12θ))=Re(e12niθsin⁡(12(n+1)θ)sin⁡(12θ))=Re((cos⁡(12nθ)+isin⁡(12nθ))sin⁡(12(n+1)θ)sin⁡(12θ))=cos⁡(nθ2)sin⁡((n+1)θ2)sin⁡(θ2).\begin{aligned} \sum_{k=0}^n \cos k\theta(\theta \not=2k\pi,k\in \mathbb{Z}) &= \sum_{k=0}^n \text{Re}(e^{ki\theta}) \\ &= \text{Re}(\sum_{k=0}^n e^{ki\theta}) \\ &= \text{Re}(\sum_{k=0}^n (e^{i\theta})^k) \\ &= \text{Re}(\frac{1-(e^{i\theta})^{n+1}}{1-e^{i\theta}}) \\ &= \text{Re}(\frac{e^{(n+1)i\theta}-1}{e^{i\theta}-1}) \\ &= \text{Re}(\frac{e^{\frac{1}{2}(n+1)i\theta}(e^{\frac{1}{2}(n+1)i\theta}-e^{-\frac{1}{2}(n+1)i\theta})}{e^{\frac{1}{2}i\theta}(e^{\frac{1}{2}i\theta}-e^{-\frac{1}{2}i\theta})}) \\ &= \text{Re}(\frac{e^{\frac{1}{2}(n+1)i\theta}2i\sin(\frac{1}{2}(n+1)\theta)}{e^{\frac{1}{2}i\theta}2i\sin(\frac{1}{2}\theta)}) \\ &= \text{Re}(e^{\frac{1}{2}ni\theta}\frac{\sin(\frac{1}{2}(n+1)\theta)}{\sin(\frac{1}{2}\theta)}) \\ &= \text{Re}((\cos(\frac{1}{2}n\theta)+i\sin(\frac{1}{2}n\theta))\frac{\sin(\frac{1}{2}(n+1)\theta)}{\sin(\frac{1}{2}\theta)}) \\ &= \frac{\cos(\frac{n\theta}{2})\sin(\frac{(n+1)\theta}{2})}{\sin(\frac{\theta}{2})}. \end{aligned}
同理有 ∑k=0nsin⁡kθ(θ≠2kπ,k∈Z)=sin⁡(nθ2)sin⁡((n+1)θ2)sin⁡(θ2)\sum_{k=0}^n \sin k\theta(\theta \not=2k\pi,k\in \mathbb{Z})=\frac{\sin(\frac{n\theta}{2})\sin(\frac{(n+1)\theta}{2})}{\sin(\frac{\theta}{2})}. 证明略。

从三角函数到巴塞尔问题

求级数 ∑k=1∞1k2\sum_{k=1}^{\infin} \frac{1}{k^2} 的值。
思路：考虑用夹逼定理求极限。联想到 0<sin⁡x<x<tan⁡x0<\sin x<x<\tan x，取平方倒数得到 cot⁡2x<1x2<csc⁡2x\cot^2 x<\frac{1}{x^2}<\csc^2 x，如果左右两个级数能够求值且相等，那么原级数就等于这两个级数的值了。
所以我们先求出这两个级数的值，再利用夹逼定理解决巴塞尔问题。
取正弦倍角公式：
sin⁡(kθ)=∑j=0[k−12](−1)j(k2j+1)cos⁡k−2j−1θsin⁡2j+1θ.\sin(k\theta)=\sum_{j=0}^{[\frac{k-1}{2}]}(-1)^j\binom{k}{2j+1}\cos^{k-2j-1}\theta\sin^{2j+1}\theta.
取 k=2n+1k=2n+1：
sin⁡((2n+1)θ)=∑j=0n(−1)j(2n+12j+1)cos⁡2n+1−2j−1θsin⁡2j+1θ.\sin((2n+1)\theta)=\sum_{j=0}^{n}(-1)^j\binom{2n+1}{2j+1}\cos^{2n+1-2j-1}\theta\sin^{2j+1}\theta.
两侧同除以 sin⁡2n+1θ\sin^{2n+1}\theta，得：
sin⁡((2n+1)θ)sin⁡2n+1θ=∑j=0n(−1)j(2n+12j+1)cos⁡2n+1−2j−1θsin⁡2j+1−2n−1θ.\frac{\sin((2n+1)\theta)}{\sin^{2n+1}\theta}=\sum_{j=0}^{n}(-1)^j\binom{2n+1}{2j+1}\cos^{2n+1-2j-1}\theta\sin^{2j+1-2n-1}\theta.
整理得：
sin⁡((2n+1)θ)sin⁡2n+1θ=∑j=0n(−1)j(2n+12j+1)cot⁡2n−2jθ.\frac{\sin((2n+1)\theta)}{\sin^{2n+1}\theta}=\sum_{j=0}^{n}(-1)^j\binom{2n+1}{2j+1}\cot^{2n-2j}\theta.
取 θ=mπ2n+1(m∈N+,m≤n)\theta=\frac{m\pi}{2n+1}(m \in \mathbb{N_+},m \le n)，得：
sin⁡(mπ)sin⁡2n+1θ=∑j=0n(−1)j(2n+12j+1)cot⁡2n−2j(mπ2n+1).\frac{\sin(m\pi)}{\sin^{2n+1}\theta}=\sum_{j=0}^{n}(-1)^j\binom{2n+1}{2j+1}\cot^{2n-2j}(\frac{m\pi}{2n+1}).
不难发现左式恒为令，因此取自变量 x=cot⁡2(mπ2n+1)x=\cot^2(\frac{m\pi}{2n+1})，就可以设计函数 f(x)=∑j=0n(−1)j(2n+12j+1)xn−jf(x)=\sum_{j=0}^{n}(-1)^j\binom{2n+1}{2j+1}x^{n-j}，使得其恰有 nn 个零点，且 xm=cot⁡2(mπ2n+1)x_m=\cot^2(\frac{m\pi}{2n+1}).
由韦达定理，得：
∑m=1ncot⁡2(mπ2n+1)=−−(2n+13)2n+1=n(2n−1)3.\sum_{m=1}^n \cot^2(\frac{m\pi}{2n+1})=-\frac{-\binom{2n+1}{3}}{2n+1}=\frac{n(2n-1)}{3}.
由恒等式 cot⁡2θ+1=csc⁡2θ\cot^2\theta+1=\csc^2\theta 得：
∑m=1ncsc⁡2(mπ2n+1)=n(2n+2)3.\sum_{m=1}^n \csc^2(\frac{m\pi}{2n+1})=\frac{n(2n+2)}{3}.
由 0<sin⁡x<x<tan⁡x0<\sin x<x<\tan x，有：
∑k=1ncot⁡2x<∑k=1n1x2<∑k=1ncsc⁡2x.\sum_{k=1}^n \cot^2 x<\sum_{k=1}^n \frac{1}{x^2}<\sum_{k=1}^n \csc^2 x.
即：
∑m=1ncot⁡2(mπ2n+1)<∑m=1n(2n+1)2m2π2<∑m=1ncsc⁡2(mπ2n+1).\sum_{m=1}^n \cot^2 (\frac{m\pi}{2n+1})<\sum_{m=1}^n \frac{(2n+1)^2}{m^2\pi^2}<\sum_{m=1}^n \csc^2 (\frac{m\pi}{2n+1}).
同乘 π2(2n+1)2\frac{\pi^2}{(2n+1)^2} 得：
π2∑m=1ncot⁡2(mπ2n+1)(2n+1)2<∑m=1n1m2<π2∑m=1ncsc⁡2(mπ2n+1)(2n+1)2.π2n(2n−1)3(2n+1)2<∑m=1n1m2<π2n(2n+2)3(2n+1)2.\frac{\pi^2\sum_{m=1}^n \cot^2 (\frac{m\pi}{2n+1})}{(2n+1)^2}<\sum_{m=1}^n \frac{1}{m^2}<\frac{\pi^2\sum_{m=1}^n \csc^2 (\frac{m\pi}{2n+1})}{(2n+1)^2}. \\ \frac{\pi^2n(2n-1)}{3(2n+1)^2}<\sum_{m=1}^n \frac{1}{m^2}<\frac{\pi^2n(2n+2)}{3(2n+1)^2}.
而 lim⁡n→+∞π2n(2n−1)3(2n+1)2=lim⁡n→+∞π2n(2n+2)3(2n+1)2=π26.\lim_{n \to +\infin} \frac{\pi^2n(2n-1)}{3(2n+1)^2}=\lim_{n \to +\infin} \frac{\pi^2n(2n+2)}{3(2n+1)^2}=\frac{\pi^2}{6}.
由夹逼定理，得 ∑k=1∞1k2=π26.\sum_{k=1}^{\infin} \frac{1}{k^2}=\frac{\pi^2}{6}.
欧拉采用的办法是对三角函数得泰勒级数因式分解，但是这种证法难以兼具简洁性和严谨性，故在此不作介绍。

评论

共 8 条评论，欢迎与作者交流。

正在加载评论...