已知 $x^2+y^2=1$，求 $(x+1)(y+2)$ 的最大值。 不妨设 $x = \sin t,y = \cos t$，即求 $(\sin t + 1)(\cos t + 2)$ 的最大值。 令 $f(t) = (\sin t + 1)(\cos t + 2)$。 可得 $f'(t) = \cos^2 t +…

推导过程较长，考察知识点较多的题。 ## 前置考虑 首先考虑**只有本身一棵树**的情况，此时是一个博弈论，从根节点 $1$ 开始，当走到一个点 $i$ 时，若现在的先手必输，记点 $i$ 为**败点**；若现在的先手必胜，记点 $i$ 为**胜点**。 显然，**叶子节点**均为败点，不可以继续往下走了，也不能往回走…

前缀和。 首先可以将破环成链的思想扩展到二维，即将原图复制四份，以样例 $3$ 为例： ``` 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 1 ``` 此时任意截取一个 $n \times n$ 的方格即为若干次移动后的结果…

贪心。 显然优先守卫 $k_i$ 更大的防御段，这样单个士兵的贡献更高。 但是该段最后可能剩下不到 $k_i$ 个敌人，此时最后一个个士兵的贡献会减少。 于是我们使用 map 统计贡献为 $x$ 的士兵数量 $y$，优先选贡献更大的士兵。 在一个防御段中，前 $\big \lfloor \frac{a_i}{k_i}…

贪心。 $2$ 次传球一定是不优的。不如直接走或传 $1$ 次再走。 更近的可传点与更远的可传点等价或更优。 每次找到左侧最近的可传点与右侧最近的可传点，与直接走的距离比较即可。 ## Code： ```cpp #include using namespace std; #define ll long long con…

构造题。 显然最后剩下 $1$，且 $h$ 最后一位一定是 $1$，否则无解。 其次，$1$ 只会出现 $1$ 或 $2$ 次，除了 $1$ 以外每个数在 $h$ 中的出现次数一定为 $1$，否则无解。 找到 $h_1$ 至 $h_{n-2}$ 未出现的两个数，因为要字典序最小，将小的那个放到最前面，大的那个放在最后面…

一个显然的树上背包。 设 $dp_{u,k,0/1}$ 表示以 $u$ 为根的子树中有 $k$ 个连通块，且 $u$ 是否在点集中的方案数。 枚举 $u$ 当前子树的连通块个数 $i$，$u$ 的子节点 $v$ 的连通块个数 $j$，转移方程： 1. $u$ 不选，$v$ 随意：$dp_{u,i+j,0}=dp_{u,…

一个显然的拆贡献，因为 $S,T$ 的组合达到了 $2^{400000}$，考虑每一个 $c_i$ 的贡献。 首先，对于一对特定的 $S,T$，有一个显然的贪心：肯定首先选择 $c_i$ 较小的那一位修改。 由于改变 $c$ 中元素的顺序不影响答案，将 $c$ 从小到大排序，对于当前位 $i$，若 $S_i = T_i…

由于 $k$ 可能很大，而最多只能有 $100$ 个点，考虑用二进制拼凑 $k$。 按照如下方法构造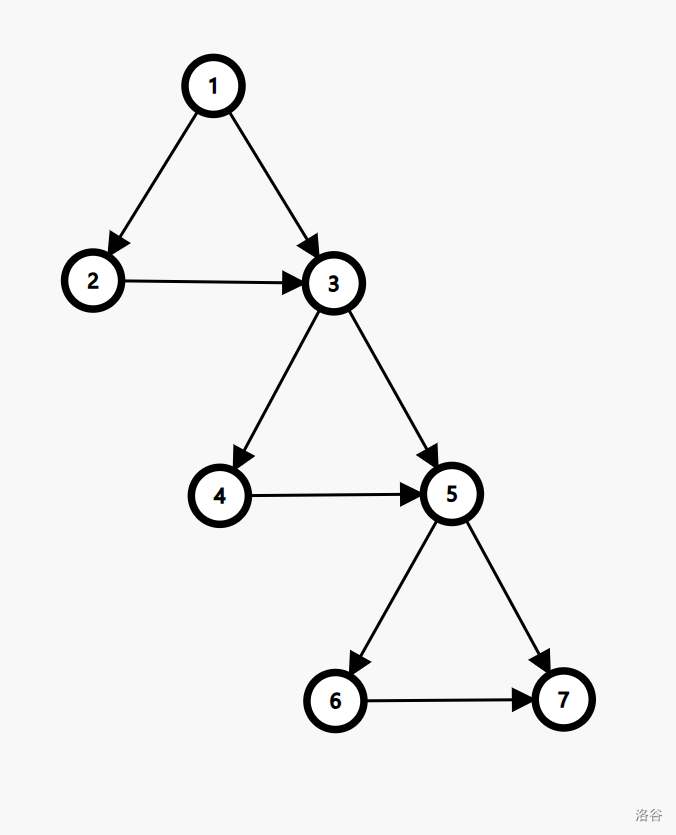：  此时到达 $2$ 的方案数为 $1$，到达 $4$ 的方案数为 $2$，到达 $6…

显然树上背包，但是每个点的贡献至多为 $1$，若该点被控制则相邻点染色时该点无贡献，故而仅使用 $dp_{i,j}$ 表示 $i$ 子树中有 $j$ 个被控制是不够的，需要多添加一些信息。 定义 $dp_{i,j,0/1/2}$ 表示 $i$ 子树中有 $j$ 个被控制，$0$ 代表 $i$ 未染色也未被控制，$1$…

## 题目大意 将 $a$ 序列前 $k$ 个数放到最后，使得 $a_1 \oplus b_1 = a_2 \oplus b_2 = \cdots = a_n \oplus b_n = x$，求满足条件的所有 $k$ 和 $x$。 ## 思路 首先有一个显然的 $O(n^2)$ 暴力，走不下去，考虑其他做法。 异或运算…

在文章《字符串学习笔记 · 浅析KMP——单模式串匹配算法》发表评论：

不觉得有什么强的

在文章《题解：P10794 『SpOI - R1』架子鼓可以站 C》发表评论：

orz sto

在文章《题解：P10794 『SpOI - R1』架子鼓可以站 C》发表评论：

dashena

在文章《题解：P10794 『SpOI - R1』架子鼓可以站 C》发表评论：

%%%

## 题目大意 题意为求 $n!$ 以内与 $m!$ 互质的数的个数（$n \ge m$）。 ## 思路 我们可以发现一个神奇的性质，由于 $n \ge m$，那么 $m! \mid n!$。然后 $m!$ 内与 $m!$ 互质的数的个数为 $\varphi(m!)$，然后 $n!$ 又为 $m!$ 的倍数，这时候就能…

## 题目大意 给定一颗树与其点权、边权，从一个点 $u$ 移动 $1$ 至其相邻点 $v$ 代价为边 $(u,v)$ 的权值 $w_{u,v}$，求将所有点权变为 $0$ 的最小代价。 ## 题目分析 首先，显然，从一个点移动 $1$ 至另一个点的最小代价是固定的，为其简单路径的边权总和，则只要不重复走边结果一定是最…

依旧卡常。空间不够，不能开数组，用滚动变量优化。 首先翻译一下题目，即序列第 $0$ 位为 $n$，若 $i \ge a_{i - 1} (1 \le i \le n)$，则 $A_i = A_{i - 1} - i$，否则 $A_i = A_{i - 1} + i$。 由于 $a_i$ 仅与 $a_{i - 1}$…

建议降黄或橙。 ## 题目分析 非常简单的分讨题，分两种情况。 1. $k \mid n$，即 $k$ 为 $n$ 的因数，枚举 $n$ 的因数，将 $n$ 中所有的 $k$ 除掉，设 $a$ 为使 $\frac{n}{k^a}$ 为整数的最大值，计 $\frac{n}{k^a} = m$，此时 $k \nmid m$…

## 题目大意 可以任意进行多次操作，每次可以选择一个叶子节点 $v$，将 $v$ 到根的简单路径中的一条边删掉，再在 $v$ 与根之间连一条边，问最终树的直径最长为多少。 ## 分析 一开始本人考虑每个子树内的最长链，最后找到根节点的两个最大子树求和，但是两条链可能在同一个子树内，这也是这道题的难点。 我们分步考虑：…

## 题目大意 根据题目模拟操作，输出 $t$ 秒后石头最多的格子里有多少个石头。 ## 分析 首先，$1 \le t \le 10^8$，暴力枚举必然超时，我们发现，操作序列的长度极短，仅有 $1$ 至 $6$，所以每 $60$ 秒为一个周期，所有操作序列均会回到第一个操作，然后循环，故考虑矩阵快速幂加速递推。 先要…

**警示后人** 1. 比赛搬原题，到处网站搬，一模一样，题面样例完全不改。 1. 比赛内容与讲的东西完全不一样，讲的不考，考了才讲，还只讲这一道题。 1. 题解生涩难懂，有的还是搬的洛谷题解（完全一样）。 1. 这几天上课净是讲一些不考、少考的内容。 1. 管理老师没打过OI，啥也不懂，平时学习不允许讨论，还因为学生…

在讨论《高斯消元当出现无数组解时如何输出任意一组解》回复：

qp

在讨论《对一类典型案例的警告》回复：

qp

在讨论《LMXOI Round2 赛后总结贴&&致歉贴》回复：

@[_Skyfire_](/user/381949) ~~可以穿bs~~

在讨论《LMXOI Round2 赛后总结贴&&致歉贴》回复：

怎么没腿啊？~~这让我怎么吃~~

在讨论《LMXOI Round2 赛后总结贴&&致歉贴》回复：

qp

在讨论《【已截止】NOI2024 游记开放投稿》回复：

qp

在讨论《NOI 2024 金钩已发放》回复：

qp

[P1593](https://www.luogu.com.cn/problem/P1593) $b$ 的范围改成 $0 \le b \le 10^{2000}$ 可做吗？ 大概难度是多少？