专栏文章
题解:P9101 [PA 2020] Skierowany graf acykliczny
P9101题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @mio03l3n
- 此快照首次捕获于
- 2025/12/02 11:10 3 个月前
- 此快照最后确认于
- 2025/12/02 11:10 3 个月前
由于 可能很大,而最多只能有 个点,考虑用二进制拼凑 。
按照如下方法构造:
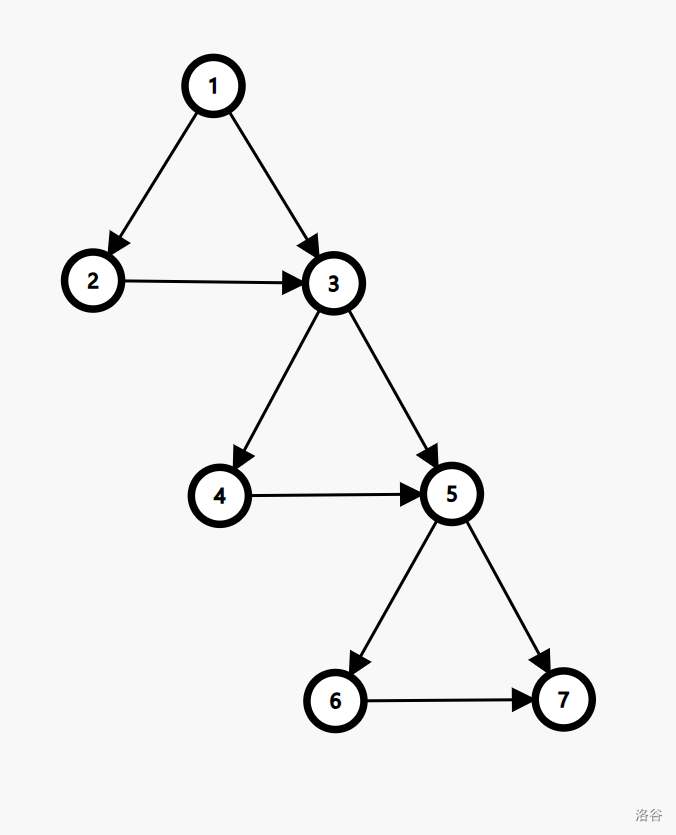
此时到达 的方案数为 ,到达 的方案数为 ,到达 的方案数为 ,以此类推,到达 的方案数为 。
此时偶数点均仅有一个出度,令终点始终为 ,若 含 就从 连一条边到 即可。注意, 和 之间不能连边。
代码
CPP#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 100050;
int k;
int main() {
cin >> k;
cout << 100 << endl;
for(int i = 1; i <= 98; i ++){
if(i & 1) cout << i + 1 << " " << i + 2 << endl;
else if((k & -k) == (1 << (i / 2 - 1))){
k ^= (k & -k);
cout << i + 1 << " " << 100 << endl;
}
else cout << i + 1 << " " << -1 << endl;
}
puts("-1 -1\n-1 -1");
return 0;
}
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...