# Day -11 生病了。 # Day -6 病好了，准备激情二连模拟赛。 # Day -2 第一次参加 WC，启程，青岛！ 飞机上头好痛，开幕式第一次听 dzd 讲话，好玩。 # Day -1 课还算能听？虽然大家都不想来就是了。 饭菜和被子啥的不错，基础设施有点差。手机不支持自动售货机呜呜呜。 晚上打牌了，好玩。…

参考了官方题解。 令 $x=\Pi p_i^{\alpha_i}$，注意到因数个数只和可重集 $\{\alpha_i\}$ 有关，所以只需要保留所有可重集 $\{\alpha_i\}$ 不同的数即可，在 $x\le 10^6$ 条件下共有 $289$ 个，记为 $m$。 容易想到先两两预处理出最短路，然后 $O(1)$…

# Day -1 CSP 前最后的模拟赛，豪赤，拼尽全力 AK 了。 # Day 0 CSP 前一天，本来上午想做题的，但是由于偶遇垃圾题，而且大家都开摆了，所以就做了一道题。下午看大家都走了就提前翘课回家了，摆了一个下午。 这是我第一次 CSP 不用参加 J 组，所以不用定酒店，只要第二天上午出发去就行了，所以也挺轻…

提供一种比较好写的小常数做法。 注意到原图由若干偶环组成，容易想到对于每个环计算其贡献。设环长为 $2n$，贡献一定要么为包含整个环，贡献为 $n$；要么是若干条链，贡献为每条链点数整除 $2$ 的值之和。 这里已经可以通过枚举链并确定链端点不取的方式直接精确计算每条链的贡献了，但是这样太麻烦了，有没有更简洁的做法呢？…

提供一种比较好写的直接构造的方法。 ::::warning[提示] 以下为笔者的思考过程，可以跳过直接看最后的构造部分。 :::: 容易想到先确定非标记点，限制每个标记点周围和为 $5$ 的倍数，这等价于在此邻域中对于每个 $1$ 存在不同且唯一的 $4$ 与其对应。注意到每个标记点四相邻标记点数为偶数，否则显然无解，…

看不懂官方题解。 显然二项式反演，定义 $g_i$ 表示恰 $i$ 个断点的方案数，$f_i$ 为选定 $i$ 个断点，剩余任意的方案数，有： $$g_i=\sum_j (-1)^{i-j}{n-1-j\choose n-1-i}f_j$$ 枚举多余断点，直接容斥易得，这一步可以卷积优化，比较平凡不再赘述。 考虑如何得…

以下为本人做这道题遇到的问题，不一定是所有人的问题，这里列出来以供参考。 - 翻译不准确，面积为所有对应的多边形面积和，只与多边形是否与圆有交有关。 - 多边形存在重点。 - 读入浮点数需要快读，其他地方也要适当注意常数，如是否有必要使用 `long double`。

提供一种与数值无关的做法，附次数证明。 分治区间 $(l,r)$，查询得对应 $(x,f)$，记区间长度为 $len$，分类讨论： - $f\le \dfrac{len}{2}$，递归 $(l,mid),(mid+1,r)$。 - $f > \dfrac{len}{2}$，查询 $(l,mid)$，得 $x_l,f_l…

提供一种好写的线性做法。 注意到单个和全部是好做的，而两个可以转化为全局加单点减同一个数，于是转化为前两者。枚举总共加的值，计算出所有第二类的取值范围相加检查即可，时间复杂度 $O(n)$。 对边界略加分讨应该可以做到 $O(1)$。 $O(n)$ 实现。 ```cpp #include using namespace…

提供最近在模拟赛看到的，一种很好写，跑的很快的优美做法。 先给结论：若将 $a,b$ 排序，分别视为 $+1,-1$，则会形成一条折线，那么只有在同一纵坐标的点会相互匹配。图是偷的。 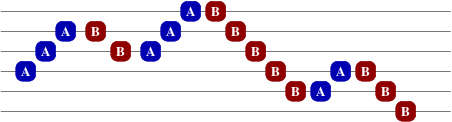 证明：注意到不存在两对相交…

提供一种 $O(n\log n)$ 的做法。 注意到题目等价于找一个有限空间内的三维长方体，所以第一类点（即第一次输入的点，下同）能够框定该长方体的最小形状，而第二类则要求其不覆盖某些位置，前者是好利用的，求出长方体最小形状之后可以通过判断第二类点和查询点是否在内部判断无解或必然可行。 而必然不可行等价于最小形状并上查…

萌新手写的一个本题函数式交互库，调试可以用一下。 ```cpp namespace Interactive{ #define maxn 370001 int n,rt,a[maxn],s[maxn],fa[maxn]; vector e[maxn],t[maxn],vec; void dfs(int x,int lst…

注意到每个位置是独立的，考虑覆盖它的所有操作，设第 $i$ 个操作执行了 $a_i$ 次，每个限制形如 $a_i+a_j=k$（可以通过建虚点补全限制）。 考虑建图，对于每个限制连接无向边 $i,j$ 边权为 $k$，显然每个连通块独立，而且每个连通块只要确定了其中一个数其他数就唯一确定，直接枚举其中一个，取最小和即可…

这里说一下不用分类讨论的简单做法。 注意到若 $k$ 合法，则 $2k(2k \lceil \frac{n}{2}\rceil$ 合法。 记 $m=\lceil \frac{n}{2}\rceil$，后缀和数组 $suf_i=\sum_{j=i}^m a_j$，即要求 $\min_{i=1}^{n-k+1}suf_i+…

赛时做法，不知道官方题解为什么这么复杂，赶紧来发个题解。 显然一个串是动听的充要条件是任意两个相同字符坐标差超过 $m+2$，即任意连续 $m+3$ 个字符两两不同。 注意到开头已经给了 $m+2$ 个字符，这启示我们直接往后填，不考虑末位字符的限制，每次要求与前面 $m+2$ 个字符均不同，有 $(k-(m+2))^…

简单题。 注意到对于 $2k>n$，满足 $a_{2k}=a_{2k+1}$，于是考虑异或前缀和，有 $pre_{2k+1}=\bigoplus_{i=1}^{2k+1} a_i= x$，其中 $x$ 可以通过任意计算一项得到。特别的，若 $n$ 为奇数，则 $a_n=x$。 而对于偶数 $pre_{2k}=pre_{…

有意思的简单题。 判定能否通过某种操作达到确定状态的题目，我们可以尝试进一步简化操作。显然每一列是 $a_i,b_i$ 或 $b_i,a_i$，不妨将列内序与列间序分开考虑。 由于我们可以同时改变列内序和列间序，所以我们考虑如何只改变列间序（列内序）。事实上，对于两列 $i,j$，只需要引入第三列 $k$，依次交换 $…

这里提供一种比较好写的时间复杂度 $O(n\log V)$ 的做法。 套路地，对于求第 $k$ 小问题，通过二分答案转化成求 $ #define maxn 510005 #define int long long using namespace std; int n,k,a[maxn],pre[maxn]; unord…

直接贪心即可。 首先，如果教学楼已经完成匹配或无限制无教授，显然可以不考虑。 注意到开始一定在没有限制的教学楼接人，然后考虑将人送到哪里。我们贪心地希望能在放人的同时接更多人，否则可以给出如下构造： ``` 3 -MCM M-MC ``` 此时如果将 1 和 2 匹配则无法继续匹配，因为并没有接到尽量多的人。另一方面，…

# 题目描述 有无穷个硬币，可均匀随机生成 $0$ 或 $1$，要求构造一种方法，生成 $0$ 到 $n-1$ 的随机整数，求最小期望抛硬币次数。 样例解释：样例 1,3 中 $n=2^k$，此时期望显然为 $k/1$；样例 2 中 $n=3$，我们给出如下构造： 首先抛两次硬币，生成两个 0/1，若结果为 `1`，则…

提供一个不用脑子的做法。 注意到答案即为矩形的并，构造如下：先填宽为 1 的矩形，如果当前区间已被某一个矩形完全覆盖，就舍去当前矩形，否则直接区间覆盖，显然最终每个矩形为开始矩形的子矩形。 然后考虑宽为 2 的，同理，不过要对于上下两行判断是否被完全覆盖，选择合适的行并赋值。 注意到我们要维护一个区间赋值，区间查询颜色…

# Day -1 期末考ing……（炸了 # Day 0 上午考完最后一门科目，直接出发去机场（每日开出校单开好久）。尽管刚刚考完直接跑路着实有点逃避的嫌疑，但对于还从来没有去过北京的我来说，对于北方的目的地，还是心怀期待和恐惧——怕水土不服考不好。 随便吃了一点，因为要期末考，所以是单独的机票。好无聊，睡了一会，就到…

在讨论《[有更新]洛谷专栏管理志愿者招募》回复：

qp

在文章《2024 NOIp 游记》发表评论：

www

# P.S. 这次是蒟蒻第一次参加 NOIP，可能写的比较水，大佬们请多多原谅。 # Day -1 模拟赛，喜提 T2 100->60，T3 也没打暴力，被小一届的同学以 70 分的分差吊打了。 # Day 0 考前一天摆烂，上午随便刷题，下午就出发了，路上堵了好久还睡了一觉。这回浙江考点又是杭师大，酒店也订了一个之前…

在讨论《求 T4 正解》回复：

Cu

如果使用了离散化，请检查您的数组大小是否足够，否则可能会出现 `RE/WA` 等错误。 本人未将离散化数组开到两倍，导致多次 `WA on test 7`，望周知。

由于吉司机线段树的时间复杂度基于势能分析，所以 `update_min` 函数的错误可能引起 #9 #10 的 TLE，从而得到 80pts 的分数。 本人的错误在于对**严格**次大值的更新，错误： ```cpp s[x].maxse=max(min(s[x s[x 100。

本题虽然数据是 $d_i,f_i\le 2\times 10^9$，但是加和会超过 `int` 限制，从而出现 `TLE`，`WA` 等错误。如果你是 $O(n\log n \log V)$ 及更优算法，理论上不会时间超限。

在讨论《APIO/THU/PKU SC 2024 游记集合贴》回复：

https://www.luogu.com.cn/article/tgcay974