专栏文章

题解：CF1214F Employment

yyingkeqian9217
CF1214F题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mioyipoz
此快照首次捕获于
2025/12/03 03:14
3 个月前
此快照最后确认于
2025/12/03 03:14
3 个月前
查看原文
提供最近在模拟赛看到的，一种很好写，跑的很快的优美做法。
先给结论：若将 a,ba,b 排序，分别视为 +1,−1+1,-1，则会形成一条折线，那么只有在同一纵坐标的点会相互匹配。图是偷的。
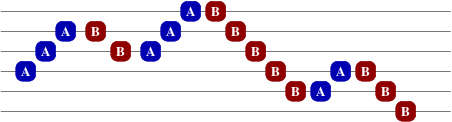
证明：注意到不存在两对相交点对异向（即 ABBA 式），故相交点对总是同向，于是可以类似于括号匹配转化为相互包含。所以答案点对总是相互不交或包含，手模一下，于是可以等价于上面。
然后因为每一层显然 AB 交替，故只有两种方式匹配，直接计算即可。
时间复杂度 O(nlog⁡n)O(n\log n)，瓶颈在排序。
CPP
#include<bits/stdc++.h>
#define maxn 2010005
#define fi first
#define se second
#define int long long
using namespace std;

int m,n,a[maxn];
vector<pair<int,int> >t[maxn];
vector<pair<int,int> >vec;
#define dist(x,y) (min(((x)+m-(y))%m,((y)+m-(x))%m))
signed main(){
	scanf("%lld%lld",&m,&n);
	for(int i=1,x;i<=n;i++) scanf("%lld",&x),vec.emplace_back(x,i);
	for(int i=1,x;i<=n;i++) scanf("%lld",&x),vec.emplace_back(x,-i);
	sort(vec.begin(),vec.end());
	int res=0,ans=0;
	for(auto i:vec){
		int x=i.fi,op=(i.se<0);
		if(!op) res++,t[res+n].emplace_back(x,i.se);
		else t[res+n].emplace_back(x,i.se),res--;
	}
	for(int i=0;i<=n+n;i++){
		int len=t[i].size(),sum1=0,sum2=0;
		for(int j=0;j<len;j++)
		 if(j&1) sum1+=dist(t[i][(j+1)%len].fi,t[i][j].fi);
		 else sum2+=dist(t[i][(j+1)%len].fi,t[i][j].fi);
		int op=(sum1<sum2);
		for(int j=op;j<len;j+=2) if(t[i][j].se>0) a[t[i][j].se]=-t[i][(j+1)%len].se;else a[t[i][(j+1)%len].se]=-t[i][j].se;
		ans+=min(sum1,sum2);
	}
	printf("%lld\n",ans);
	for(int i=1;i<=n;i++) printf("%lld ",a[i]);printf("\n");
	return 0;
}

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...