写于 NOI2025 的疏散日，一场决定除我以外许多人命运的比赛。 去年 NOI 之后，似乎我接受的比较快，但更不如说是让自己处于麻木状态。闭幕式都没去就直接回去了，尽量不去想 NOI 的事。 什么心情？不时会想，xxx 有什么理由比我更应该进队？ 但不过是迁怒罢了，现在审视我 NOI 前的训练状态明显有问题，看似每天…

在讨论《省队选拔 2024 游记集合贴》回复：

https://www.luogu.com.cn/article/wmtesrpy

在讨论《NOI 2023 游记集合贴》回复：

https://www.luogu.com.cn/blog/tiatto/noi2023-you-ji

在讨论《关于返祖边 dep 大小关系的问题》回复：

@[lTgMFePRoeZ](/user/115194) 可以不是后代。如果有横叉边 $(x\to y)$，因为是强连通所以也一定存在 $y\to rt$ 的路径。设 $\gcd$ 为 $d$，则 $len_{rt,y}+len_{y,rt}\mod d= 0$，则 $(len_{rt,x}+1+len_{y,rt})…

在讨论《关于返祖边 dep 大小关系的问题》回复：

但是强连通分量内是可以有横叉边的

在讨论《关于这题的题解》回复：

这是删了又重新挂上去了吗 @[kkksc03](/user/1)

在讨论《关于这题的题解》回复：

@[chen_zhe](/user/8457)

请问题解审核志愿者是完全不审内容吗？完全是瞎扯的东西都能放过。

在讨论《沪爷陈哲你必须身败名裂。》回复：

这么猛

在讨论《APIO 2023 游记集合贴》回复：

https://www.luogu.com.cn/blog/tiatto/apio2023-post

在讨论《2023 省选游记集合贴》回复：

https://www.luogu.com.cn/blog/tiatto/its-all-but-a-dream

在讨论《求 t2 树部分分做法》回复：

不用背包，考虑小于 $sz<l$ 的点一定不选，$sz\geq r$ 的点一定选，$=l$ 的讨论一下就行。@[2018ljw](/user/128606)

在讨论《HK有学的必要吗》回复：

dinic 不是这个复杂度吗

在讨论《【OI相关，学术】如果把高考数学题换成OI题，是否有复杂度较低写法》回复：

莫反

在讨论《求广义容斥原理的证明》回复：

建议重修线性代数。

在讨论《求广义容斥原理的证明》回复：

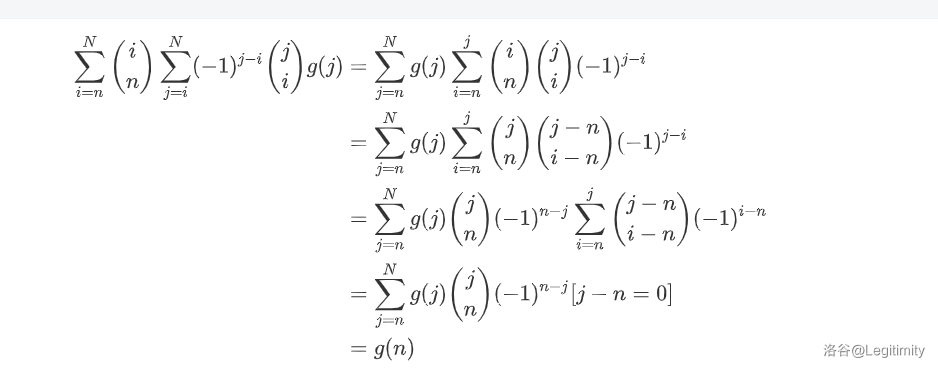 两者本质没有区别，转换成线性变换后矩阵都是类似的，就和莫反的两种形式、集合或卷积与集合并卷积本质相同一个道理。@[StillEmpty](/user/150956)

在讨论《为什么我用广义二项式定理推出来是这个样子的》回复：

@[rxjdasiwzl](/user/96446) 这不是一样的吗 

在讨论《为什么我用广义二项式定理推出来是这个样子的》回复：

哦您是指下面那个式子是吗，那个确实是错的 /kk @[hs_white](/user/261773)

在讨论《为什么我用广义二项式定理推出来是这个样子的》回复：

$$ \binom{-n}{i}(-1)^i=\binom{i+n-1}{i} $$ 这应该没错吧？

在讨论《为什么我用广义二项式定理推出来是这个样子的》回复：

翻转上指标为什么下指标会变 

在讨论《关于校内赛应不应该出不出原题这件事，请大家评定一下》回复：

校内训练赛为什么不能放原题啊，有那么多原创套题给平时训练吗？

在讨论《萌新求助Dirichlet逼近定理》回复：

/fad

在讨论《萌新求助Dirichlet逼近定理》回复：

似乎没问题（？

在讨论《萌新求助Dirichlet逼近定理》回复：

@[wkywkywky](/user/133954) 设 $k=aT+b$，枚举 $a$ 插入 $\{aTx\}$，枚举 $b$ 时查找 $[0,1/Q-\{bx\}]$ 和 $[1-\{bx\},1+1/Q-\{bx\}]$

在讨论《萌新求助Dirichlet逼近定理》回复：

感觉这种问题总有人类智慧 $\log$ 做法 /fad

在讨论《萌新求助Dirichlet逼近定理》回复：

@[渐变色](/user/224584) 感觉挺暴力的，就原问题等价于求$1\leq q\leq Q,\{qx\}\leq \dfrac{1}{Q}$，用抽屉原理证明时是证明存在 $0\leq a<b\leq Q,|\{ax\}-\{bx\}|\leq \dfrac{1}{Q}$，然后 $|\{ax\}-\{bx\}|…

在讨论《萌新求助Dirichlet逼近定理》回复：

@[Legitimity](/user/241977) 但应该对任意实数都可以

在讨论《萌新求助Dirichlet逼近定理》回复：

我现在只想到一个 $O(\sqrt Q)$ 的暴力做法 /kk

在讨论《萌新求助Dirichlet逼近定理》回复：

@[Epsilon_Cube](/user/372983) 当然指的是 $Q$……这您自己根据描述看不出来吗……

在讨论《萌新求助Dirichlet逼近定理》回复：

@[Epsilon_Cube](/user/372983) $Q$ 可以小于 $n$