-1. 前言
最近突击了一下高中必修一 A 版的三角函数部分,整合了一下知识点。这篇文章非常通俗易懂,这里有
PDF 版本,喜欢的给个赞吧()
0. 锐角三角函数(高中生可跳过)
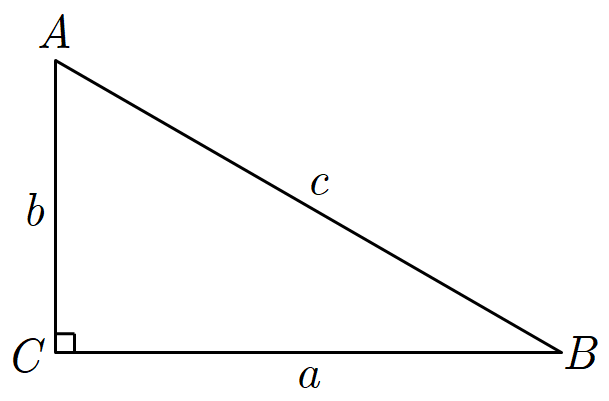
如图,在
Rt△ABC 中,
∠C=90°,则
∠A 的正弦
sinA=ca(对比斜),余弦
cosA=cb(邻比斜),正切
tanA=ba(对比邻),这三个函数就被称为
锐角三角函数,一般配合直角三角形使用,在初中阶段主要用于解直角三角形。
举个例子,如果在上面的直角三角形中有
tanB=33,BC=3,那么则有
∠A=60°,∠B=30°,AC=1,AB=2。
以下是特殊角的三角函数表(其实可以全部手模出来)。
| 三角函数 / α 度数 | 0° | 30° | 45° | 60° | 90° |
|---|
| sinα | 0 | 21 | 22 | 23 | 1 |
| cosα | 1 | 23 | 22 | 21 | 0 |
| tanα | 0 | 33 | 1 | 3 | / |
当你把
0 看作
20,
21 看作
21,
1 看作
24 时,会明显好记很多。
1. 任意角与弧度制
1.1 任意角
容易发现,在锐角三角函数中,
sin 和
cos 定义域都为
[0°,90°],
tan 定义域为
[0°,90°),都局限在一个比较小的范围内。能不能让定义域扩展到全体实数呢?下面我们引入
任意角。
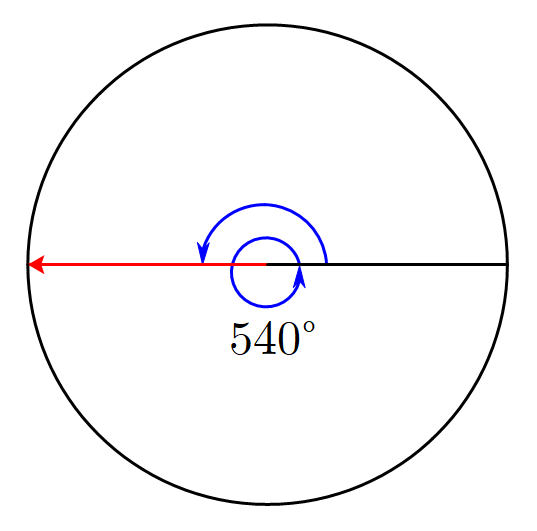
啥是任意角?顾名思义,任意角的度数为全体实数。比如在新闻中会出现“前空翻转体
540°”等词,这里的度数就可表示为
540°。我们接下来把这样的任意角放在一个
单位圆(半径为
1 的圆)上,这样逆时针绕圆一周就是
360°,顺时针就是
−360°,如图。
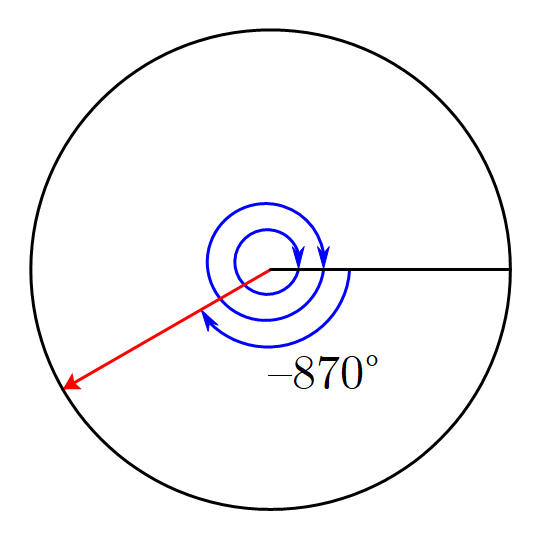
再比如
−870°,如图。
因此,我们可以把角的概念抽象为一条射线绕其端点按一定方向旋转一定角度形成的图形,逆时针旋转就是正角,顺时针就是负角。任意角的加减运算法则是显然的,如图。
加上一个正角就是逆时针旋转,负角就是顺时针。
我们可以令这个单位圆的圆心为直角坐标系的原点,之后构建一个直角坐标系,这样一个角的始边一定在
x 轴上。我们规定,这个角的
终边在哪个象限就是第几象限角。
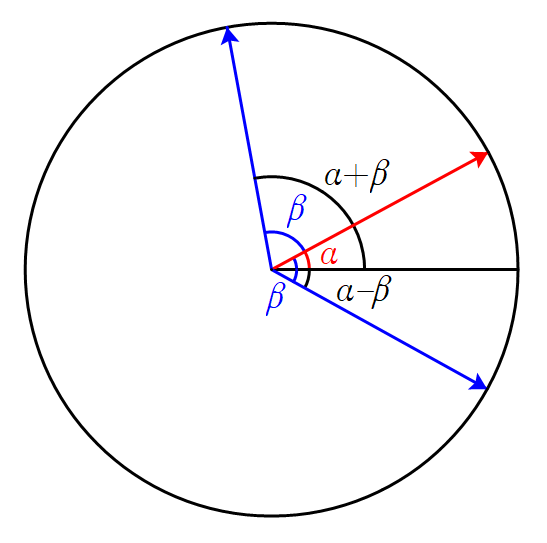
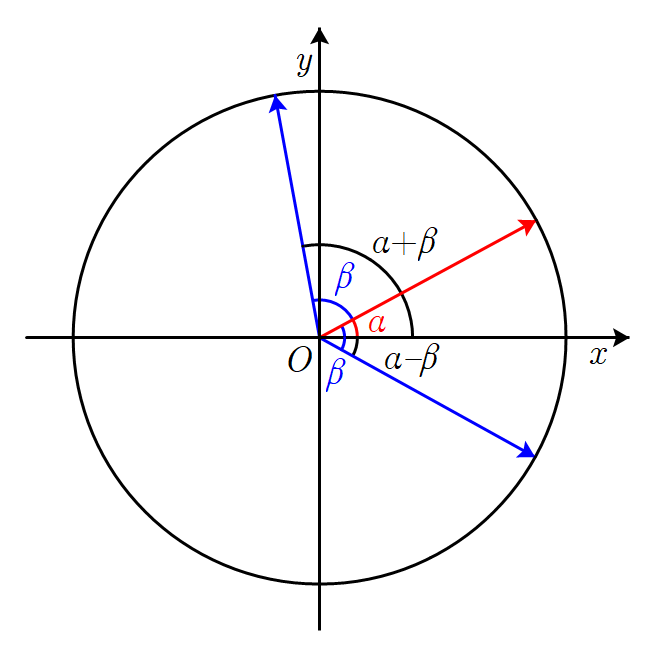
如图,
α,β 为第一象限角,令
γ=α+β,δ=α−β,则
γ 为第二象限角,
δ 为第四象限角。因为一个角的终边旋转
360° 与原边重合,所以若存在一个角
α,则所有
β=α+360°k(k∈Z) 的终边都与
α 的终边相等。
1.2 弧度制
我们小学就学过角度制,单位为
°,比如
114°,51° 等,但是当我们把角放进单位圆中后,一个角度多多少少得跟
π 有点关系,所以我们引入与
π 有关的
弧度制。
因为单位圆的周长为
2π,所以我们规定,一个周角就是
2π 弧度的角。弧度的单位为
rad,所以有
360°=2π rad。同理,因为平角是周角的一半,所以有
180°=π rad。