专栏文章
高中数学笔记
学习·文化课参与者 200已保存评论 234
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 233 条
- 当前快照
- 1 份
- 快照标识符
- @miqpxj6p
- 此快照首次捕获于
- 2025/12/04 08:49 3 个月前
- 此快照最后确认于
- 2025/12/04 08:49 3 个月前
基本完备的高中数学笔记,相比之前的增加了集合部分,优化了阅读体验,删改了部分题目。
请注意阅读本文的内存消耗。( 约 GB )
已经开源:here
方程求解
-
代数基本定理:任何一元 次复系数多项式方程 至少有一个复数根。
-
一元一次方程
-
一元二次方程
-
一元三次方程
-
盛金公式重根判别式总判别式
-
-
令
-
-
其中
-
卡尔达诺公式先左右除以 ,令 得到一个奇数次的方程 ,再令 得到瞪眼法可以知道 的一个根,再解出 即可。
-
-
一元四次方程顺着这样的形式容易将 韦达定理推广到一元 次方程。
-
二元一次方程组
集合
基本概念
-
集合:某些指定的对象集在一起就形成一个集合( 简称集 )。
-
元素:集合中每个对象叫做这个集合的元素。
-
集合的三要素:
-
确定性:集合内的元素是可以被确定的,比如:“七大洲”就是一个集合,“数学中的所有难题”就不是一个集合,因为你无法确定难题的标准是什么。
-
互异性:集合内的各元素都是唯一不重复的。
-
无序性:集合内的各元素的顺序是没有限制的,比如集合 与集合 是一样的。
-
-
常见的集合:非负正数集( 自然数集 ) 正整数集 或 整数集 有理数集 实数集
-
集合的两种常用表达方式 列举法:用 把所有元素包括在一起,注意各元素之间用逗号隔开适应于元素数量较少,如集合 . 描述法:用某种元素之间的规律表示集合,比如所有奇数的集合 或者不等式 的解集 .
集合间的关系
表示某一元素属于某个集合时,用 ,例如 . 若不属于则用 .
| 名称 | 记号 | 意义 | 性质 |
|---|---|---|---|
| 子集 | 或 | 中的任意元素都属于 | 且 且 |
| 真子集 | 或 | 且 中至少有一元素不属于 | 且 |
基本运算
- 并集:.
- 交集:.
- 补集:,若 ,则 .
交换律:.
结合律:.
分配对偶律:.
德·摩根定律:.
推广到多个集合中:
若记 表示集合 的元素个数。例如:. 那么集合 的子集数为 ,真子集数为 .
常用逻辑用语
充分条件、必要条件、充要条件
- 若 ,则称 是 的充分条件, 是 的必要条件。
- 若 ,则称 是 的充分必要条件,即充要条件。
全称量词与存在量词
全称量词:“所有的”,“任意一个”,用 表示,即倒过来的 A(All).
存在量词:“存在一个”,“至少一个”,用 表示,即倒过来的 E(Exist).
全称量词命题:对 中的任意一个 成立,即 ,否定是 .
存在量词命题:存在 中的元素 成立,即 ,否定是 .
不等式
以下
均值不等式
对于 ,有
也就是 调和平均值 几何平均值 算术平均值 平方平均值。取等条件:
加权形式: 且 ,有 .
比较常用的二元形式:
三元形式:
对于对勾函数 ,对 且 当且仅当 .
-
已知 ,求 的最小值。
- 注意 .
-
已知 ,求证 .设 ,则 .同理可得 ,代入原式得使用基本不等式化简,取等条件 ,即 .注:在数学中 表示左边的式子,同理 表示右边的式子。
-
,则
最大值为 最小值为
最小值为 最小值为
答案:
提示: 中 .
类似构造:,求 的最小值 ?答案:.
- 设 是正实数,则 的最小值为 ?
柯西-施瓦茨不等式
二元形式:,当 时取等。
三元形式:,当 取等。
例 1:已知 ,求 最小值。
当且仅当 取等。
例 2:求函数 的最大值。
当 时,最后的结果是常数。结合不等式等号成立条件
可以得出 .
例 3:【增量换元】【2006 CMO T1】设实数 满足 ,求证:
不妨设 且 ,设 ,于是只用证
注意到 于是
利用柯西不等式,
例 4:【2023 IMO T4】设 为两两不等的正实数,使得对每个 ,
都是一个整数,求证:.
观察数字,发现只需证明 ,这样 。
所以 ,很显然了。
推论:权方和不等式
若 ,则
取等条件:.
常见的二元形式:,取等条件 .
还可以推广为:若 ,则
- 当 时,
- 当 时,
- 当 时,
取等条件都是 .
例 1:已知 ,求 的最小值。
例 2:已知 ,求 的最小值。
练:已知 ,求 的最小值。答案:
推论: 卡尔松不等式
其表述是:在 矩阵中,各列元素之和的几何平均不小于各行元素的几何平均之和,当 时即为柯西二维形式。
例:正数 满足 ,求 的最小值。
其他推论
设 ,则
证明:对 进行归纳。当 时显然成立。当 时直接平方柯西即证。假设 时成立, 时:
于是原不等式成立。
奥采尔不等式
设整数 是实数,满足 ,那么
当且仅当 时成等号成立。规定 时 .
常见的二元形式:,当 时取等。
例 1:求 最小值。
当且仅当 即 时取等。
练 1:求 最小值。答案:.
练 2:求 最小值。答案:.
总结:对于 的最小值是 ,此时 .
例 2:求 最小值。
所以 ,在 取等。
伯努利不等式
若实数 各项符号相同,且 ,则:
取等条件显然为
当 相等时,变为如下三种形式:( 全部都要求 )
- 当 或 时,
- 当 时,
广义伯努利不等式:设实数 或 ,有
例:欲证明 ,有
幂平均不等式
取等条件:.
加权形式:
切比雪夫不等式
若 ,则:
取等条件: 或 .
常见的二元形式:若 则 .
排序不等式
若 ,则:正序和 乱序和 反序和。
取等条件: 或 .
赫尔德不等式( 高次柯西 )
更常用的形式是:
琴生不等式
设 为单调区间 的下凸函数,表示对任意 均有
则对任意 及 均有
外森比克不等式
设 为三角形三边, 为此三角形面积,则
等号成立条件:,几何意义:以三边分别做等边三角形,其面积之和大于等于原三角形的面积的 倍。
推广:若 ,则
证明:过点 作 的垂线 ,记 ,则
分别用了权方和不等式和均值不等式证明,取等条件 且 .
闵可夫斯基不等式
设实数 ,则
取等条件:对应 与 成比例。
注意:当 时,不等式反向。
乘积形式:设 ,则
舒尔不等式
设 ,则( 表示轮换对称和 )
一般地,舒尔不等式为:设 ,则
证明:不妨设 ,则 。
舒尔不等式有两个变形非常有用:
嵌入不等式
设 是三角形 的三个内角,则对任意实数 有
例题:【2007 CTST T4】设正实数 满足 ,求证:
设 ,有 ,只用证 ,设 ,只用证
这很显然了。
其他关于三角的不等式:如果 并且 ,那么
当且仅当 或者 .
绝对值不等式
不等式
例子
-
若实数 满足 , 则 的最大值是 ?使用判别式法,令 代入得
-
已知正实数 满足 , 则正实数 的最大值是 ?
-
中求 的最大值。所求式中 等价,故 时取最值 .当然考试不能这么写,这里给出一个正经做法:令 ,那么 由于 ,所以 ,求导可知当 时也就是 为等边三角形时取等。
-
若正实数 满足 且 ,求 的范围. 考虑消去 ,而 ,得到 ,由 得 . 于是 .
-
【2001 IMO T2】求证:
【高考证法】
首先注意到 时等号成立。其次,每个分数的“阶”都是“零次”( 分母是二次,开方后一次,相除后零次 ),这种分数可令
将 化为 ,注意这时不能用柯西不等式,否则更加麻烦,是条死路。于是只能通分,化为等价的:
两边平方得
由 化简,只用证下述 成立即可。
因 ,所以 ,于是
证毕。
【竞赛证法】
由权方和不等式得
关于证 :即证 ,均值即得。
此外还有反证法等等。

和式的恒等变换
阿贝尔变换
对于两个数列 ,记 为 前缀和,那么
那么可以很快地算出 “等差 等比 ” 这类数列的前缀和。
例 1:求值 .
令 ,则
令 ,则 .
例 2:证明:.
令 ,则
因为
所以
解不等式即可证左边。下证右侧。令 ,则
解得 .
函数
复合函数单调性——同增异减
以下用箭头 表示函数单调递增,箭头 表示函数单调递减。
奇偶性
-
奇函数:对称中心 ,如 .
-
偶函数:关于 对称,如 .
-
一个多项式函数为奇函数,当且仅当它只有奇数次幂,如 .
-
一个多项式函数为偶函数,当且仅当它只有偶数次幂,如 .
-
-
-
反函数:定义域和值域与原函数互换的新函数,如 的反函数为 ,反之亦然。例:已知函数 ,则 的的图像恒过定点 的反函数的图像恒过定点 ,即横坐标与纵坐标互换。反函数的其他性质:原函数与其反函数关于直线 对称。
-
。
-
奇偶函数加减法则
- 复合函数奇偶性( )
| 奇 | 奇 | 奇 |
| 奇 | 偶 | 偶 |
| 偶 | 奇 | 偶 |
| 偶 | 偶 | 偶 |
对称性
必记二级结论
-
关于 对称。
-
的对称中心为 .
以下记 为函数的周期, 记 为某个常数。
-
-
-
-
-
关于 对称
-
的两个对称中心
-
关于 对称且有个对称中心
拓展二级结论
-
三次及以下的多项式函数具有一般对称性,四次及以上的多项式函数不具有一般对称性。最高幂次为奇数的多项式函数只可能具有中心对称性,最高幂次为偶数的多项式函数只可能具有轴对称性。如果一个多项式函数 具有中心对称性,那么它的对称中心为 .如果一个多项式函数 具有轴对称性,那么它的对称轴 .
-
的对称中心 .注意到该函数的定义域为 ,值域是 .例: 的对称中心 ?首先我们知道,这三个式子的对称中心分别是 ,,.如果这个函数有对称中心,其横坐标就在 中间即 .因为函数是三个式子相加,所以纵坐标就是三个纵坐标相加即 .所以函数的对称中心 .
-
的对称中心 即 .
-
的对称中心 .
-
关于 对称 且 在 时与 的单调性相同。
-
任何一个函数 都可以拆分为 之和。
-
.
-
.
-
关于 中心对称 是奇函数。
函数图像的变化
参考:here
平移:下加上减,左加右减
向上平移 :将方程中所有 替换成 .
向下平移 :将方程中所有 替换成 .
向左平移 :将方程中所有 替换成 .
向右平移 :将方程中所有 替换成 .
例如:将 的图像向右平移 个单位,向下平移 个单位得到
伸缩
以 轴为轴伸缩到原来的 倍:将方程中所有 替换成 .
以 轴为轴伸缩到原来的 倍:将方程中所有 替换成 .
若要以其他直线为轴伸缩,那么就先平移过去再伸缩,若直线是倾斜的如 还要加上旋转一步。
旋转
对于任何方程,将其图像绕原点顺时针旋转 ,只需要将其表达式中所有 替换为 ,将所有 替换为 . 逆时针旋转 相当于顺时针旋转 .
例如:将 绕原点顺时针旋转 得到
对称
将点 沿 轴对称变为 ,沿 轴对称变为 .
将方程的图像沿 轴对称就将所有 替换成 ,沿 轴对称就将所有 替换成 .
若将直线沿 对称,记倾斜角为 ,那么将所有 替换成 ,将所有 替换成
常见抽象函数及其模型
-
-
证单调性/奇偶性:
-
-
-
证单调性/奇偶性:
-
-
-
-
求值域
-
分离常数例:求 值域,先求出定义域 .令对 分类讨论后使用基本不等式。综上所述,取最值时 .
-
三角换元( 形如 求最值 )例:求 的值域,先求出定义域 .令 且其中 ,除去根号可得值域 .
-
数形结合( 将军饮马,圆,斜率... )例 1:求 最小值?转化为求 之间的距离 答案 .例 2: 的最小值 ?当 时,令 , 显然, 的含义是点 与单位圆上的点 的连线的斜率的平方。注意到,,所以 .
基本计算
对数
| 加法 | 减法 | 换底公式 |
|---|---|---|
例子
-
例 1:已知正实数 满足 ,则 ( )令 ,则 ,,. 易证 选项不成立。显然有 即 ,可证得 选项成立。选项题意转化得 ,易证其成立。选项即证明
-
例 2:设 ,比较大小。
复数
-
模或绝对值 定义 .共轭复数 几何意义:复平面( 横轴为实轴,纵轴为虚轴 )上点注意实部为 ,虚部为 ( 不带 ) 注意当 时为纯虚数, 不是纯虚数。所有虚数( )均不能直接比较大小,如 ,当且仅当 变成实数时才可以比较。
-
运算:对于 ,有
-
对于 .
-
一个题:已知 为方程 的根,则 ?( 单位圆的性质 )
一些性质
复数与复平面
-
在复平面内对应点的集合是以原点为圆心, 为半径的圆。在复平面内对应点的集合是以 在复平面内的对应点为圆心, 为半径的圆。在复平面内对应点的集合是 为端点的线段的中垂线。
-
设复数 在复平面内对应点为 ,结合平面向量的基本运算。四边形 为矩形。四边形 为菱形。且 四边形 为正方形。
-
综合题:已知复数 满足 ,若 ,则 的最大值是 ?
复数的三角表示
其中 .
规定在 时 为辐角的主值,记为 ,且满足 .
-
设 ,则
-
棣莫弗定理:对于 ,满足
另外,借助棣莫弗定理可以推导 等公式。
- 复数 的 次方根是
因此要注意 表示 个复数。
- 可以推导 .
复数的指数形式
我们把模为 ,辐角为 的复数 用 表示。例如
于是对任意复数均满足
对于复数的乘除,对应到指数就是加减。对于开方运算,
题目
- 求值:.
考虑复数 ,题目相当于计算 的辐角,于是答案为
- 已知复数 ,且 ,求 的值。
- 已知复数 且 ,求 的最大值。
设 ,则
当 取等,即 .
三角恒等变换
诱导公式
-
毕达哥拉斯定理:,两边同除 或 可得
-
-
奇函数: 偶函数:.
简单的三角恒等变换
- , 其中 , 时,最好检验一下 位于第二象限还是第四象限。
-
对于任意非直角三角形中,总有 .经典值:, 此时 .
-
其他三角形恒等式( 中 ):
-
若已知 则有 .
-
.
-
对于 .
例 1:若 为锐角 且满足 ,若 ,求 .
我们知道正切恒等式 。其证明:
我们又知道
于是 ,也即 .
因为 ,所以 ,所以 ,由正切恒等式解方程得 .
例 2:在 中,,求 最大值。
三角函数的平移
-
三角函数的应用:振幅 周期 频率 相位 初相
-
-
三角函数里图像的平移都是针对单个 进行 左加右减。例: 向左平移 个单位长度,再将图像上所有点的横坐标缩短为原来的 :第一步转移变成 .第二步转移变成 .
三角不等式
若 为同一个三角形的内角,则有下列不等式:( 取等条件均为 ,可以使用琴生不等式、调整法等证明 )
双曲函数
并且满足 .
倍角公式
\cos\theta & 1 & 0 & \cdots & 0 & 0 \\
1 & 2\cos\theta & 1 & \cdots & 0 & 0 \\
0 & 1 & 2\cos\theta & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & \cdots & 2\cos\theta & 1 \\
0 & 0 & 0 & \cdots & 1 & 2\cos\theta
\end{vmatrix}=\sum_{k=0}^nC_n^k\cos^k x\sin^{n-k} x\cos\frac{(n-k)\pi}{2}\end{aligned}$$
$$\begin{aligned}\sin n\theta&=\begin{vmatrix}
\sin\theta & 0 & 0 & \cdots & 0 & 0 \\
0 & 2\cos\theta & 1 & \cdots & 0 & 0 \\
0 & 1 & 2\cos\theta & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & \cdots & 2\cos\theta & 1 \\
0 & 0 & 0 & \cdots & 1 & 2\cos\theta
\end{vmatrix}=\sum_{k=0}^nC_n^k\cos^k x\sin^{n-k} x\sin\frac{(n-k)\pi}{2}\end{aligned}$$
求 $S=\sin 1\degree\sin 2\degree\dots\sin 89\degree\sin 90\degree$ 的值。
反复运用三倍角公式 $\displaystyle\sin x\sin(60\degree-x)\sin(60\degree+x)=\frac{1}{4}\sin3x$ 即可。
$$\begin{aligned}S&=(\sin 1\degree\sin 59\degree\sin 61\degree)(\sin 2\degree\sin 58\degree\sin 62\degree)\dots(\sin 29\degree\sin 31\degree\sin 89\degree)\sin 30\degree\sin 60\degree\sin 90\degree\\&=\left(\frac{1}{4}\right)^{30}\sqrt{3}(\sin 3\degree\sin 6\degree\dots\sin 87\degree)\\&=\left(\frac{1}{4}\right)^{30}\sqrt{3}(\sin 3\degree\sin 57\degree\sin 63\degree)\dots(\sin 27\degree\sin 33\degree\sin 87\degree)\sin 30\degree\sin 60\degree\\&=\left(\frac{1}{4}\right)^{40}3(\sin 9\degree\sin 18\degree\dots\sin 81\degree)=\left(\frac{1}{4}\right)^{40}3(\sin 9\degree\cos 9\degree)\dots(\sin 36\degree\cos 36\degree)\sin 45\degree\\&=\left(\frac{1}{4}\right)^{42}\frac{3\sqrt{2}}{2}\sin 18\degree\cos 18\degree\sin 36\degree\cos 36\degree=\left(\frac{1}{4}\right)^{43}\frac{3\sqrt{2}}{2}\sin 36\degree\cos 18\degree=\left(\frac{1}{4}\right)^{45}6\sqrt{10}\end{aligned}$$
### 其他
$$2\sum_{1\leq i<j\leq n}\cos(a_i-a_j)=\left(\sum_{i=1}^n\cos a_i\right)^2+\left(\sum_{i=1}^n \sin a_i\right)^2-n$$
$$\tan(\alpha+\beta+\gamma)=\frac{\tan\alpha+\tan\beta+\tan\gamma-\tan\alpha\tan\beta\tan\gamma}{1-\tan\alpha\tan\beta-\tan\alpha\tan\gamma-\tan\beta\tan\gamma}$$
等差三角函数求和的半角裂项:( 和差化积 )
$$\sum_{k=0}^n\cos(x+kd)=\frac{\cos(x+\frac{n}{2}d)\sin\frac{n+1}{2}d}{\sin\frac{d}{2}}$$
$$\sum_{k=0}^n\sin(x+kd)=\frac{\sin(x+\frac{n}{2}d)\sin\frac{n+1}{2}d}{\sin\frac{d}{2}}$$
$$\sin\frac{d}{2}\sin(a_0+nd)=\frac{1}{2}\left[\cos\left(a_0+\left(n-\frac{1}{2}\right)d\right)-\cos\left(a_0+\left(n+\frac{1}{2}\right)d\right)\right]$$
$$\sin\frac{d}{2}\cos(a_0+nd)=\frac{1}{2}\left[-\sin\left(a_0+\left(n-\frac{1}{2}\right)d\right)+\sin\left(a_0+\left(n+\frac{1}{2}\right)d\right)\right]$$
---
$$\sin nA+\sin nB+\sin nC=\begin{cases}\displaystyle 4\sin\frac{n\pi}{2}\cos\frac{nA}{2}\cos\frac{nB}{2}\cos\frac{nC}{2},\ n=2k+1\\ \displaystyle -4\cos\frac{n\pi}{2}\sin\frac{nA}{2}\sin\frac{nB}{2}\sin\frac{nC}{2},\ n=2k\end{cases}$$
$$\cos nA+\cos nB+\cos nC=\begin{cases}\displaystyle 1+4\sin\frac{n\pi}{2}\sin\frac{nA}{2}\sin\frac{nB}{2}\sin\frac{nC}{2},\ n=2k+1\\ \displaystyle -1+4\cos\frac{n\pi}{2}\cos\frac{nA}{2}\cos\frac{nB}{2}\cos\frac{nC}{2},\ n=2k\end{cases}$$
$$\tan nA+\tan nB+\tan nC=\tan nA\tan nB\tan nC$$
特例:
$$n=1\begin{cases}\displaystyle \sin A+\sin B+\sin C=4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}\in\left(0,\frac{3\sqrt{3}}{2}\right]\\\displaystyle\cos A+\cos B+\cos C=1+4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}=1+\frac{r}{R}\in\left(1,\frac{3}{2}\right]\\\displaystyle\tan A+\tan B+\tan C=\tan A\tan B\tan C\end{cases}$$
另外:
$$\begin{cases}\displaystyle\sin\frac{A}{2}+\sin\frac{B}{2}+\sin\frac{C}{2}=1+\sin\frac{\pi-A}{4}\sin\frac{\pi-B}{4}\sin\frac{\pi-C}{4}\in\left(0,\frac{3}{2}\right]\\\displaystyle\cos\frac{A}{2}+\cos\frac{B}{2}+\cos\frac{C}{2}=4\cos\frac{\pi-A}{4}\cos\frac{\pi-B}{4}\cos\frac{\pi-C}{4}\in\left(0,\frac{3\sqrt{3}}{2}\right]\\\displaystyle\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2}=\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2}\\\displaystyle\tan\frac{A}{2}\tan\frac{B}{2}+\tan\frac{B}{2}\tan\frac{C}{2}+\tan\frac{C}{2}\tan\frac{A}{2}=1\\\displaystyle\sin^2A+\sin^B+\sin^2C=2+2\cos A\cos B\cos C\\\displaystyle\cos^2A+\cos^2B+\cos^2C=1-2\cos A\cos B\cos C\end{cases}$$
最后两个其实是下列三元三角恒等式的变形:( 其中 $\displaystyle\theta=\frac{\alpha+\beta+\gamma}{2}$ )
记 $A=\cos\theta\cos(\theta-\alpha)\cos(\theta-\beta)\cos(\theta-\gamma),B=\sin\theta\sin(\theta-\alpha)\sin(\theta-\beta)\sin(\theta-\gamma)$
$$\cos\alpha\cos\beta\cos\gamma=A+B\ \ \ \ \ \ \frac{1}{4}(\cos 2\alpha+\cos 2\beta+\cos 2\gamma+1)=A-B$$
三角形中费马点 $P$ 满足:
$$PA:PB:PC=\frac{\displaystyle\sin\left(A+\frac{\pi}{3}\right)}{\sin A}:\frac{\displaystyle\sin\left(B+\frac{\pi}{3}\right)}{\sin B}:\frac{\displaystyle\sin\left(C+\frac{\pi}{3}\right)}{\sin C}$$
$$PA+PB+PC=\sqrt{b^2+c^2-2bc\cos\left(A+\frac{\pi}{3}\right)}=\sqrt{a^2+2bc\cos\left(A-\frac{\pi}{3}\right)}$$
角平分线长:$\displaystyle t_a=\frac{2}{b+c}\sqrt{bcp(p-a)}=\frac{bc}{b+c}\sqrt{2(\cos A+1)}=\frac{2bc}{b+c}\cos\frac{A}{2}$
中线长:$\displaystyle m_a=\sqrt{\frac{\displaystyle b^2+c^2-\frac{a^2}{2}}{2}}=\frac{\sqrt{b^2+c^2+2bc\cos A}}{2}$
# 平面向量
### 定义及基本运算
- 我们把既有大小又有方向的量称为向量,把只有大小没有方向的量称为数量。向量用有向线段 $\overrightarrow{AB}$ 表示( 但向量 $\neq$ 有向线段 ),它的长度即模记作 $|\overrightarrow{AB}|$.
长度等于 $1$ 个单位长度的向量,称为单位向量,一般用 $\mathbf{e}$ 或 $\overrightarrow{e}$ 表示( 前者为印刷体,后者为手写体,以下均使用清晰易辨的手写体格式 )。长度等于 $0$ 个单位长度的向量,称为零向量,用 $\overrightarrow{0}$ 表示,它的方向是任意的。坐标轴不能说是向量( 没有长度 )。
- 平行向量 / 共线向量:方向 **相同 或 相反** 的非零向量叫做平行向量。零向量与任何向量平行。所以 $\overrightarrow{a}//\overrightarrow{b},\overrightarrow{b}//\overrightarrow{c}\ \xcancel{\implies}\ \overrightarrow{a}//\overrightarrow{c}$.
向量 $\overrightarrow{a}(\overrightarrow{a}\neq\overrightarrow{0})$ 与 $\overrightarrow{b}$ 共线 $\Longleftrightarrow$ 存在唯一一个实数 $\lambda$ 使 $\overrightarrow{b}=\lambda\overrightarrow{a}$.
- 相等向量:长度相等 且 方向相同的两个向量。相反向量:长度相等 且 方向相反的两个向量。
- 投影向量:设 $\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{CD}=\overrightarrow{b}$,过 $\overrightarrow{AB}$ 的起点 $A$ 和终点 $B$,分别作 $\overrightarrow{CD}$ 所在直线的垂线,垂足分别为 $A_1,B_1$ 并得到 $\overrightarrow{A_1B_1}$,称上述变换为向量 $\overrightarrow{a}$ 向向量 $\overrightarrow{b}$ 投影,$\overrightarrow{A_1B_1}$ 叫做向量 $\overrightarrow{a}$ 在向量 $\overrightarrow{b}$ 上的投影向量。
- 两个向量之间的夹角可用 $\theta=\langle\overrightarrow{a},\overrightarrow{b}\rangle$ 表示,注意两个向量此时必须共顶点。
| $\theta$ | $0$ | $\pi$ | $\displaystyle\frac{\pi}{2}$ |
| :---------------------------------: | :-------------------------------: | :-------------------------------: | :----------------------------------------------------------------: |
| $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的关系 | $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 同向 | $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 反向 | $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 垂直 记作 $\overrightarrow{a}\perp\overrightarrow{b}$ |
| 运算符 | 运算法则 | 性质 |
| :------------------------------: | :---------------------------------------------------------------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------: |
| $+$ | 平行四边形法则 | |
| $-$ | 转化为相反向量后用平行四边形法则 | $-\overrightarrow{AB}=\overrightarrow{BA}$ |
| 数乘 | 实数 $\lambda$ 与向量 $\overrightarrow{a}$ 的积仍是向量,记作 $\lambda\overrightarrow{a}$ | $\| \lambda\overrightarrow{a} \| = \| \lambda \| \| \overrightarrow{a} \|$,满足交换律,结合律 |
| 点乘 $\cdot \\$ ( 内积/数量积 ) | $\overrightarrow{a}\cdot\overrightarrow{b}=\|\overrightarrow{a}\|\|\overrightarrow{b}\|\cos\theta,\theta=\langle \overrightarrow{a},\overrightarrow{b} \rangle$ | $\overrightarrow{a}\perp\overrightarrow{b}\Longleftrightarrow\overrightarrow{a}\cdot\overrightarrow{b}=0,\|\overrightarrow{a}\cdot\overrightarrow{b}\|\leq\|\overrightarrow{a}\|\|\overrightarrow{b}\|$,满足交换律,**不满足结合律,不能约分**$\\$ 即 $(\overrightarrow{a}\cdot\overrightarrow{b})\overrightarrow{c}\neq\overrightarrow{a}(\overrightarrow{b}\cdot\overrightarrow{c})$,但 $(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{c}=\overrightarrow{a}\cdot\overrightarrow{c}+\overrightarrow{b}\cdot\overrightarrow{c}$ |
| 叉乘 $\times \\$ ( 外积/向量积 ) | $\overrightarrow{a}\times\overrightarrow{b}=\overrightarrow{c}$,其中 $\\ \|\overrightarrow{c}\|=\|\overrightarrow{a}\|\|\overrightarrow{b}\|\sin\theta,\theta=\langle \overrightarrow{a},\overrightarrow{b} \rangle$ | |
向量的 $+,-,$ 数乘运算统称为向量的线性运算,向量线性运算的结果仍为向量。点乘运算叫做 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 的数量积/内积,结果为数量。
### 定理及二级结论
- 平面向量基本定理:若 $\overrightarrow{e_1},\overrightarrow{e_2}$ 是同一平面内的两个不共线向量,则对于这一平面内的任意向量 $\overrightarrow{a}$,有且只有一对实数 $\lambda _1,\lambda _2$,使得 $\overrightarrow{a}=\lambda _1\overrightarrow{e_1}+\lambda _2\overrightarrow{e_2}$.
若 $\overrightarrow{e_1},\overrightarrow{e_2}$ 不共线,我们把 $\set{\overrightarrow{e_1},\overrightarrow{e_2}}$ 叫做这一平面内所有向量的一个 **基底**;任一向量都可以由同一个基底唯一表示。
- 定比分点公式:已知点 $D$ 为线段 $BC$ 靠近点 $B$ 的第 $k$ 个 $n$ 等分点,则有 $$ \red{\boxed{\overrightarrow{AD}=\frac{k}{n}\overrightarrow{AC}+\frac{n-k}{n}\overrightarrow{AB}}}$$ 其中 $A$ 为平面内任取的一点。
已知 $A(x_1,y_1),B(x_2,y_2),P(x,y)$,若 $\overrightarrow{AP}=\lambda\overrightarrow{PB}$,则 $\displaystyle x=\frac{x_1+\lambda x_2}{1+\lambda},y=\frac{y_1+\lambda y_2}{1+\lambda}$.
- $||\overrightarrow{a}|-|\overrightarrow{b}||\leq|\overrightarrow{a}\pm\overrightarrow{b}|\leq|\overrightarrow{a}|+|\overrightarrow{b}|$,应用不等式时,必须验证 **等号成立的条件**。
- $|\overrightarrow{a}|=|\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|\implies$ 正三角形 $\ \ \ \ \ \ \ \ \text{}$ $|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|\implies$ 矩形
$|\overrightarrow{a}|=|\overrightarrow{b}|\implies$ 菱形 $\ \ \ \ \ \ \ \ \text{}$ $|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|$ 且 $|\overrightarrow{a}|=|\overrightarrow{b}|\implies$ 正方形
- 正弦定理:$\displaystyle\red{\boxed{\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{a+b+c}{\sin A+\sin B+\sin C}=2R=D}}$,其中 $R$ 为三角形外接圆半径,$D$ 为直径。
例如:已知 $(a+b)(\sin A-\sin B)=(c-b)\sin C$,可转化为 $$(a+b)(a-b)=(c-b)c\implies b^2+c^2-a^2=bc\implies\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{1}{2}$$
注意 $\sin C=\sin(\pi-(A+B))=\sin(A+B)=\sin A\cos B+\cos A\sin B$.
- 余弦定理:$\red{\begin{cases}
a^2=b^2+c^2-2bc\cos A \\
b^2=a^2+c^2-2ac\cos B \\
c^2=a^2+b^2-2ab\cos C
\end{cases}\implies\begin{cases}
\displaystyle\cos A=\frac{b^2+c^2-a^2}{2bc} \\
\displaystyle\cos B=\frac{c^2+a^2-b^2}{2ac} \\
\displaystyle\cos C=\frac{a^2+b^2-c^2}{2ab}\end{cases}}$
- 正切定理:$\displaystyle\frac{a+b}{a-b}=\frac{\tan\frac{a+b}{2}}{\tan\frac{a-b}{2}}$
- 任意三角形射影定理( 将 $\cos$ 展开即可证明 ):$\red{\boxed{\begin{cases}
a=b\cos C+c\cos B \\
b=a\cos C+c\cos A \\
c=a\cos B+b\cos A
\end{cases}}}$
- 极化恒等式:$\displaystyle\overrightarrow{a}\cdot\overrightarrow{b}=\left(\frac{\overrightarrow{a}+\overrightarrow{b}}{2}\right)^2-\left(\frac{\overrightarrow{a}-\overrightarrow{b}}{2}\right)^2$
对于平行四边形 $ABCD$,满足 $\displaystyle AC^2+BD^2=2(AB^2+AD^2),\overrightarrow{AB}\cdot\overrightarrow{AD}=\frac{1}{4}(\overrightarrow{AC}^2-\overrightarrow{BD}^2)$.
对于三角形 $ABC$,$M$ 为 $BC$ 中点,$\displaystyle \overrightarrow{AB}\cdot\overrightarrow{AC}=\overrightarrow{AM}^2-\frac{1}{4}\overrightarrow{BC}^2=\overrightarrow{AM}^2-\overrightarrow{BM}^2$.
- 对任意四边形 $ABCD$,若两对角线相垂直,则 $\displaystyle S=\frac{1}{2}|\overrightarrow{AC}||\overrightarrow{BD}|$.
- 中线长定理:对于三角形 $ABC$,$AD$ 为 $BC$ 边上的中线,则有 $AB^2+AC^2=2(AD^2+BD^2)\\ \overrightarrow{AB}\cdot\overrightarrow{AC}=|\overrightarrow{AD}|^2-|\overrightarrow{BD}|^2$.
- 张角定理:$\Delta ABC,D$ 在 $BC$ 上,令 $\angle BAD=\alpha,\angle CAD=\beta$,则有 $\displaystyle\red{\boxed{\frac{\sin\alpha}{AC}+\frac{\sin\beta}{AB}=\frac{\sin(\alpha+\beta)}{AD}}}$.
- 奔驰定理:点 $O$ 是 $\Delta ABC$ 所在平面内不与 $A,B,C$ 重合的一点,若 $x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}=\overrightarrow{0},xyz\neq 0$,则 $S_{\Delta OBC}\overrightarrow{OA}+S_{\Delta OAC}\overrightarrow{OB}+S_{\Delta OAB}\overrightarrow{OC}=\overrightarrow{0}$,且 $\red{\boxed{S_{\Delta OBC}:S_{\Delta OAC}:S_{\Delta OAB}=x:y:z}}$.
证明:$\displaystyle x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}=\overrightarrow{0} \implies \frac{x}{y}\overrightarrow{OA}+\overrightarrow{OB}+\frac{z}{y}\overrightarrow{OC}=\overrightarrow{0}$.
将 $OA$ 延长到 $OE$ 满足 $\displaystyle OE=\frac{x}{y}OA$,$OC$ 延长到 $OF$ 满足 $\displaystyle OF=\frac{z}{y}OC$,变为 $\overrightarrow{OE}+\overrightarrow{OB}+\overrightarrow{OF}=\overrightarrow{0}$. 因此 $O$ 为 $\Delta EBF$ 重心,于是有 $S_{\Delta OBE}=S_{\Delta OEF}=S_{\Delta OBF}$,$$\frac{S_{\Delta AOC}}{S_{\Delta EOF}}=\frac{\frac{1}{2}OA\cdot OC\cdot \sin\angle AOC}{\frac{1}{2}OE\cdot OF\cdot\sin\angle EOF}=\frac{y}{x}\cdot\frac{y}{z}=\frac{y^2}{xz}$$
同理根据相似 $\displaystyle S_{\Delta AOC}:S_{\Delta AOB}:S_{\Delta BOC}=\frac{y^2}{xz}:\frac{yz}{xz}:\frac{xy}{xz}=y:z:x$.
例题:$\Delta ABC$ 中,$D$ 为 $BC$ 中点,$BE=2EA$,$AD$ 与 $CE$ 交于 $O$,$\displaystyle\overrightarrow{AB}\cdot\overrightarrow{AC}=6\overrightarrow{AO}\cdot\overrightarrow{EC},\frac{AB}{AC}=(\ \sqrt{3}\ \text{})$
方法一:$\displaystyle\overrightarrow{AO}=\lambda\overrightarrow{AD}=\frac{\lambda}{2}(\overrightarrow{AB}+\overrightarrow{AC})=(1-\mu)\overrightarrow{AE}+\mu\overrightarrow{AC}=\frac{1-\mu}{3}\overrightarrow{AB}+\mu\overrightarrow{AC}$.
解方程得 $\displaystyle\lambda=\frac{1}{2},\mu=\frac{1}{4},\ \overrightarrow{AO}=\frac{1}{4}\overrightarrow{AB}+\overrightarrow{AC},\overrightarrow{EC}=-\frac{1}{3}\overrightarrow{AB}+\overrightarrow{AC}$.
代入题目,$\displaystyle\frac{1}{2}AB^2=\frac{3}{2}AC^2,\frac{AB}{AC}=\sqrt{3}$.
方法二:作 $AB$ 另一个三等分点 $F$,连接 $DF$ 构造中位线。
### 平面向量的坐标表示
- 在平面直角坐标系中,设与 $x$ 轴,$y$ 轴方向相同的两个单位向量分别为 $\overrightarrow{i},\overrightarrow{j}$,取 $\{\overrightarrow{i},\overrightarrow{j}\}$ 作为基底,对于平面内任意一个向量 $\overrightarrow{a}$,有且只有一对实数 $x,y$,使得 $\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j},(x,y)$ 就是 $\overrightarrow{a}$ 的坐标,记作 $\overrightarrow{a}=(x,y)$.
显然,$\overrightarrow{i}=(1,0),\overrightarrow{j}=(0,1),\overrightarrow{0}=(0,0)$,$\overrightarrow{OA}=x\overrightarrow{i}+y\overrightarrow{j} \Longleftrightarrow A$ 的坐标 $(x,y)$.
若表示向量 $\overrightarrow{a}$ 的有向线段的起点和终点的坐标分别为 $(x_1,y_1),(x_2,y_2)$,则 $\overrightarrow{a}=(x_2-x_1,y_2-y_1)$.
- 若 $\overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2)$,则有 $\overrightarrow{a}\pm\overrightarrow{b}=(x_1\pm x_2,y_1\pm y_2),\overrightarrow{a}\cdot\overrightarrow{b}=x_1x_2+y_1y_2$.
$\lambda\overrightarrow{a}=(\lambda x_1,\lambda y_1),|\overrightarrow{a}|=\sqrt{x_1^2+y_1^2}$.
向量 $\overrightarrow{a},\overrightarrow{b}$ 共线 $\Longleftrightarrow x_1y_2=x_2y_1$;向量 $\overrightarrow{a}\perp\overrightarrow{b} \Longleftrightarrow x_1y_2=x_2y_1$.
$\displaystyle\theta=\langle\overrightarrow{a},\overrightarrow{b}\rangle\implies\cos\theta=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}\implies$ 柯西不等式的二元形式。
#### 笛卡尔斜坐标系
$x$ 轴与 $y$ 轴的角度为 $\theta\ (\theta\neq\frac{\pi}{2})$ 的坐标系。定义平面直角坐标系中的点 $P(x,y)$,将 $P$ 转移到斜坐标系中变成 $P'(x',y')$ 满足:
$$\begin{cases}x'=x+y\cos\theta \\ y'=y\sin\theta\end{cases}\ 和\ \begin{cases}\displaystyle x=x'-\frac{y'}{\tan\theta} \\ \displaystyle y=\frac{y'}{\sin\theta}\end{cases}$$
于是我们可以把平面向量在平面直角坐标系中的一些运算迁移到斜坐标系中:
- 数量积:$(x_1',y_1')\cdot(x_2',y_2')=x_1x_2+y_1y_2+(x_1y_2+x_2y_1)\cos\theta$
- 模长:$\overrightarrow{a}=(x',y'),|\overrightarrow{a}|=\sqrt{x^2+y^2+2xy\cos\theta}$
- 夹角:$\displaystyle\overrightarrow{a}=(x_1',y_1'),\overrightarrow{b}=(x_2',y_2'),\cos\gamma=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$
例题:$\Delta ABC$ 中,$D,E$ 为 $BC$ 上的两个三等分点,$\overrightarrow{AB}\cdot\overrightarrow{AD}=2\overrightarrow{AC}\cdot\overrightarrow{AE}$,则 $\cos\angle ADE$ 的最小值为 ?
以 $\overrightarrow{DC},\overrightarrow{DA}$ 的方向作为平面 $ABC$ 斜坐标系中 $x',y'$ 轴的正方向,并设 $|\overrightarrow{DA}|=m,|\overrightarrow{DC}|=2$,可得 $A(0,m),B(-1,0),C(2,0),D(0,0),E(1,0)$.
于是 $\overrightarrow{AB}\cdot\overrightarrow{AD}=(-1,-m)\cdot(0,-m)=m^2+m\cos\angle ADE$,$\overrightarrow{AC}\cdot\overrightarrow{AE}=(2,-m)\cdot(1,-m)=2+m^2-3m\cos\angle ADE$.
根据题意整理得 $\displaystyle\cos\angle ADE=\frac{1}{7}\left(m+\frac{4}{m}\right)\geq\frac{4}{7}$.
### 三角形
#### 三角形四心
以下记连接顶点和各交点的直线延长至顶点对边为 $AD,BE,CF$,设 $\Delta ABC$ 的外接圆半径为 $R$,$K$ 为平面内任意一点,$\lambda,\mu,\eta\in\R^+$.
| $\Delta ABC$ | 重心 $G$ | 垂心 $H$ |
| :------: | :-------------------: | :------: |
| 交点 | 中线 | 高 |
| 基本性质 | $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0} \\ \displaystyle\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$ | $\overrightarrow{HA}\cdot\overrightarrow{HB}=\overrightarrow{HB}\cdot\overrightarrow{HC}=\overrightarrow{HC}\cdot\overrightarrow{HA}\\AH\cdot HD=BH\cdot HE=CH\cdot CF$ | | |
| 坐标 | $\displaystyle G\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right)$ | $\displaystyle H\left(\frac{\frac{a}{\cos A}x_1+\frac{b}{\cos B}x_2+\frac{c}{\cos C}x_3}{\frac{a}{\cos A}+\frac{b}{\cos B}+\frac{c}{\cos C}},\frac{\frac{a}{\cos A}y_1+\frac{b}{\cos B}y_2+\frac{c}{\cos C}y_3}{\frac{a}{\cos A}+\frac{b}{\cos B}+\frac{c}{\cos C}}\right)$ |
| 边的向量表示 | $\because\overrightarrow{AG}=\lambda(\overrightarrow{AB}+\overrightarrow{AC}) \\ \therefore\overrightarrow{KG}=\overrightarrow{KA}+\lambda(\overrightarrow{AB}+\overrightarrow{AC})\\=\overrightarrow{KA}+\lambda\left(\frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|\sin B}+\frac{\overrightarrow{AC}}{\|\overrightarrow{AC}\|\sin C}\right)$ | $\because \lambda\left(\frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|\cos B}+\frac{\overrightarrow{AC}}{\|\overrightarrow{AC}\|\cos C}\right)\perp\overrightarrow{BC}\\ \text{} \\ \therefore\overrightarrow{KH}=\overrightarrow{KA}+\lambda\left(\frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|\cos B}+\frac{\overrightarrow{AC}}{\|\overrightarrow{AC}\|\cos C}\right)$ |
| 面积 | $S_{\Delta BGC}=S_{\Delta AGC}=S_{AGB}$ | $S_{\Delta BHC}:S_{\Delta AHC}:S_{\Delta AHB}=\tan A:\tan B:\tan C \\ \tan A\cdot\overrightarrow{HA}+\tan B\cdot\overrightarrow{HB}+\tan C\cdot\overrightarrow{HC}=\overrightarrow{0}$ |
| 定理 | $\\ 中线定理\begin{cases}\displaystyle AD^2=\frac{2b^2+2c^2-a^2}{4}\\ \displaystyle BE^2=\frac{2a^2+2c^2-b^2}{4}\\ \displaystyle CF^2=\frac{2a^2+2b^2-c^2}{4}\end{cases}\\$ 中线长定理( $AB \to \overrightarrow{AB}$ ) $\\ AB^2+AC^2=2AD^2+2DB^2$ | |
| 其余等量关系 | $1. \min\set{KA\cdot KB\cdot KC}=GA\cdot GB\cdot GC\\ 2.$ 三角形中势能最小的点为重心,即 $\\ \begin{aligned}&\mathrm{min}\set{KA^2+KB^2+KC^2}\\&=GA^2+GB^2+GC^2\end{aligned}$ 二者都可用解析几何证明 | $AH=2R\|\cos A\|\ \ \ \ \ BH=2R\|\cos B\|\ \ \ \ \ CH=2R\|\cos C\|\\HD:HE:HF=\|\cos B\cos C\|:\|\cos C\cos A\|:\|\cos A\cos C\|\\ HA^2+BC^2=HB^2+CA^2=HC^2+AB^2$ |
| **$\Delta ABC$** | **内心 $I$** | **外心 $O$** |
| :------: | :-------------------: | :------: |
| 交点 | 内角平分线 | 垂直平分线 |
| 基本性质 | $I$ 到三条边的距离相等 $\\ \begin{cases}\overrightarrow{IA}\cdot\left(\frac{\overrightarrow{AC}}{\|\overrightarrow{AC}\|}-\frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|}\right)=\overrightarrow{0} \\ \overrightarrow{IB}\cdot\left(\frac{\overrightarrow{BC}}{\|\overrightarrow{BC}\|}-\frac{\overrightarrow{BA}}{\|\overrightarrow{BA}\|}\right)=\overrightarrow{0} \\ \overrightarrow{IC}\cdot\left(\frac{\overrightarrow{CB}}{\|\overrightarrow{CB}\|}-\frac{\overrightarrow{CB}}{\|\overrightarrow{CA}\|}\right)=\overrightarrow{0}\end{cases}\\$ 以上三条公式括号内两向量可互换 | $OA=OB=OC \\ \angle_{AOB}=2\angle_C\ \ \ \ \angle_{AOC}=2\angle_B\ \ \ \ \angle_{BOC}=2\angle_A\\ \begin{cases}\displaystyle\overrightarrow{AO}\cdot\overrightarrow{AB}=\frac{1}{2}\|\overrightarrow{AB}\|^2 \\ \displaystyle\overrightarrow{AO}\cdot\overrightarrow{AC}=\frac{1}{2}\|\overrightarrow{AC}\|^2\\ \displaystyle\overrightarrow{BO}\cdot\overrightarrow{BC}=\frac{1}{2}\|\overrightarrow{BC}\|^2\end{cases}$ |
| 坐标 | $\displaystyle I\left(\frac{ax_A+bx_B+cx_C}{a+b+c},\frac{ay_A+by_B+cy_C}{a+b+c}\right)$ | $\displaystyle O\left(\frac{\sin 2Ax_1+\sin 2Bx_2+\sin 2Cx_3}{\sin 2A+\sin 2B+\sin 2C},\frac{\sin 2Ay_1+\sin 2By_2+\sin 2Cy_3}{\sin 2A+\sin 2B+\sin 2C}\right)$ |
| 边的向量表示 | $\begin{aligned}\overrightarrow{AI}&=\lambda\left(\frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|}+\frac{\overrightarrow{AC}}{\|\overrightarrow{AC}\|}\right)\\&=\mu\left(\sin B\cdot\overrightarrow{AB}+\sin C\cdot\overrightarrow{AC}\right)\\&=\eta\left(\frac{\overrightarrow{AB}}{\sin C}+\frac{\overrightarrow{AC}}{\sin B}\right)\end{aligned}$ | $\displaystyle\overrightarrow{KO}=\frac{\overrightarrow{KB}+\overrightarrow{KC}}{2}+\lambda\left(\frac{\overrightarrow{AB}}{\|\overrightarrow{AB}\|\cos B}+\frac{\overrightarrow{AC}}{\|\overrightarrow{AC}\|\cos C}\right) \\ \text{} \\ \Delta ABC$ 的外心在 $O$ 点的集合中 |
| 面积 | $S_{\Delta BIC}:S_{\Delta AIC}:S_{\Delta AIB}=a:b:c\\a\cdot\overrightarrow{IA}+b\cdot\overrightarrow{IB}+c\cdot\overrightarrow{IC}=\overrightarrow{0}$ | $S_{\Delta BOC}:S_{\Delta AOC}:S_{\Delta AOB}=\sin 2A:\sin 2B:\sin 2C\\\sin 2A\cdot\overrightarrow{OA}+\sin 2B\cdot\overrightarrow{OB}+\sin 2C\cdot\overrightarrow{OC}=\overrightarrow{0}$ |
| 定理 | **角平分线定理** $ AD$ 平分 $\angle BAC \implies \frac{AB}{BD}=\frac{AC}{CD}\\$ **鸡爪定理** $\\$ $AI$ 交 $\Delta ABC$ 外接圆于 $D$ 有 $ID=DB=DC$ | |
| 其余等量关系 | $\|\overrightarrow{BC}\|\cdot\overrightarrow{IA}+\|\overrightarrow{AC}\|\cdot\overrightarrow{IB}+\|\overrightarrow{AB}\|\cdot\overrightarrow{IC}=\overrightarrow{0} \\ \displaystyle AI:BI:CI=\frac{1}{\sin\frac{A}{2}}:\frac{1}{\sin\frac{B}{2}}:\frac{1}{\sin\frac{C}{2}}$ | $\begin{cases}\overrightarrow{AO}\cdot\overrightarrow{AD}=\frac{1}{4}(\|\overrightarrow{AB}\|^2+\|\overrightarrow{AC}\|^2) \\ \overrightarrow{BO}\cdot\overrightarrow{BE}=\frac{1}{4}(\|\overrightarrow{BA}\|^2+\|\overrightarrow{BC}\|^2) \\ \overrightarrow{CO}\cdot\overrightarrow{CF}=\frac{1}{4}(\|\overrightarrow{CA}\|^2+\|\overrightarrow{CB}\|^2)\end{cases}\\ \begin{cases}\overrightarrow{AO}\cdot\overrightarrow{BC}=\frac{1}{2}(\|\overrightarrow{AC}\|^2-\|\overrightarrow{AB}\|^2) \\ \overrightarrow{BO}\cdot\overrightarrow{AC}=\frac{1}{2}(\|\overrightarrow{BC}\|^2-\|\overrightarrow{BA}\|^2) \\ \overrightarrow{CO}\cdot\overrightarrow{AB}=\frac{1}{2}(\|\overrightarrow{CB}\|^2-\|\overrightarrow{CA}\|^2)\end{cases}$ |
- 内接圆半径 $$r=\frac{\tan\frac{A}{2}(b+c-a)}{2}$$
- 欧拉定理:$O,I$ 分别为外接圆、内切圆圆心,则有 $OI^2=R^2-2Rr$.
- 欧拉线定理:三角形的外心 $O$,垂心 $H$,重心 $G$ 依次位于同一直线上,且重心到外心的距离是重心到垂心的距离的一半,即 $$\red{\boxed{\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OH}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})}}$$
- 锐角三角形外心到三边距离之和等于 $R+r$.
证明:等价于证 $R(\cos A+\cos B+\cos C)=R+r$,我们知道
$$\frac{1}{2}(a+b+c)r=S_{\Delta ABC}=S_{\Delta OAB}+S_{\Delta OAC}+S_{\Delta OBC}=\frac{1}{2}R(a\cos A+b\cos B+c\cos C)$$
联立上两式( 相乘 ),则需证
$$(a+b+c)(\cos A+\cos B+\cos C)=a+b+c+a\cos A+b\cos B+c\cos C$$
直接展开易知等式成立。
例题:根据欧拉线定理,在 $\Delta ABC$ 中有 $AB=2,AC=3$,以下正确的有( $\text{ACD}$ )
$\text{A}.\ \overrightarrow{AH}\cdot\overrightarrow{BC}=\overrightarrow{0}\ \ \ \ \ \text{B}.\ \displaystyle\overrightarrow{AG}\cdot\overrightarrow{BC}=-\frac{5}{3}\ \ \ \ \ \text{C}.\ \overrightarrow{AO}\cdot\overrightarrow{BC}=\frac{5}{2}\ \ \ \ \ \text{D}.\ \overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$
对 $\text{A}$,因为 $H$ 为垂心,所以 $AH\perp BC$,显然正确。
对 $\text{B}$,$\displaystyle\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}),\ \overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\implies\overrightarrow{AG}\cdot\overrightarrow{BC}=\frac{5}{3}$.
对 $\text{C}$,$\displaystyle\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB},\ \overrightarrow{AO}\cdot\overrightarrow{AB}=\frac{1}{2}|\overrightarrow{AB}|^2,\ \overrightarrow{AO}\cdot\overrightarrow{AC}=\frac{1}{2}|\overrightarrow{AC}|^2$.
对 $\text{D}$,$\displaystyle\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OH},\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\implies\overrightarrow{OG}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})=\frac{1}{3}\overrightarrow{OH}$.
#### 三角形面积公式
以下记 $S$ 为三角形面积,$r$ 为三角形内切圆半径,$R$ 为三角形外接圆半径。
- 海伦公式:$\displaystyle p=\frac{a+b+c}{2},S=\sqrt{p(p-a)(p-b)(p-c)},r=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}$.
- 利用 $\sin$:$\displaystyle \red{\boxed{{S=\frac{bc\sin A}{2}=\frac{ab\sin C}{2}=\frac{ac\sin B}{2}}}}=\frac{a^2\sin B\sin C}{2\sin A}=\frac{b^2\sin A\sin C}{2\sin B}=\frac{c^2\sin A\sin B}{2\sin C}$
- 内切圆:$\displaystyle S=\frac{r(a+b+c)}{2}$, 外接圆:$\displaystyle S=2R^2\sin A\sin B\sin C=\frac{abc}{4R}$, 注意可与 正弦定理 连用。
- 多边形面积( 皮克定理 ):$\displaystyle S=a+\frac{b}{2}-1$,其中 $a$ 为多边形内部的点数,$b$ 为多边形落在格点上的点数。
- 等边三角形面积:$\displaystyle S=\frac{\sqrt{3}}{4}a^2$,其中 $a$ 为等边三角形边长。
- 在 $\Delta ABC$ 中,已知 $\displaystyle \overrightarrow{AB}=(x_1,y_1), \overrightarrow{AC}=(x_2, y_2)\implies \red{\boxed{{S=\frac{1}{2}|x_1y_2-x_2y_1|}}}$
例 1:已知锐角三角形里 $\displaystyle B=\frac{\pi}{3},c=2$,求 $S$ 范围?
$$\frac{a}{\sin A}=\frac{c}{\sin C}\implies a=\frac{c\sin A}{\sin C}=\frac{2\sin A}{\sin(\frac{2\pi}{3}-A)}$$
$$S=\frac{ac\sin B}{2}=\frac{\sqrt{3}}{2}\cdot\frac{c\sin A}{\sin C}=\frac{\sqrt{3}}{2}\cdot\frac{2\sin A}{\sin(\frac{2\pi}{3}-A)}=\frac{\sqrt{3}\sin A}{\frac{\sqrt{3}}{2}\cos A+\frac{1}{2}\sin A}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2\tan A}+\frac{1}{2}}$$
$$\frac{\pi}{6}<A<\frac{\pi}{2}\implies\tan A>\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{2}<\frac{\sqrt{3}}{\frac{\sqrt{3}}{2\tan A}+\frac{1}{2}}<2\sqrt{3}$$
例 2:$\Delta ABC$ 中满足 $4\sqrt{3}S=a^2+b^2+c^2$,求 $\displaystyle\frac{2a}{3b+c}$ 的值?
由 $\displaystyle S=\frac{1}{2}ab\sin C$ 和 $c^2=a^2+b^2-2ab\cos C$ 得到 $ab(\sqrt{3}\sin C+\cos C)=a^2+b^2$.
$\displaystyle 2\sin\left(C+\frac{\pi}{6}\right)=\frac{a^2+b^2}{ab}\implies\frac{a^2+b^2}{ab}\geq\frac{2ab}{ab}=2$ ( 当且仅当 $a=b$ 时取等 )
$\therefore \Delta ABC$ 为等边三角形,$\displaystyle\frac{2a}{3b+c}=\frac{1}{2}$.
其实题干给的就是外森比克不等式取等的情况,可直接得出 $a=b=c$.
同样的一道练习题:实数 $a,b,c$ 满足 $\displaystyle e^{a-b+c}+e^{a+b-c}=2e^2(a-1)$,求 $\displaystyle\left(\frac{abc}{a^4+b^4+c^4}\right)_{\max}$.
答案:$\displaystyle\frac{\sqrt{2}}{8}$,此时 $b^4=c^4=8,a=2$.
#### 求三角形内最值问题
已知 $\Delta ABC$,$D$ 在边 $BC$ 上。
1. 已知 $\displaystyle\frac{BD}{CD},AD,\cos\angle_{BAC}\implies$ **向量法**,$(\overrightarrow{AD})^2=[x\overrightarrow{AB}+(1-x)\overrightarrow{AC}]^2,\displaystyle S=\frac{1}{2}AB\cdot AC\cdot\sin\angle_{BAC}$.
2. 已知 $AD\perp BC,AD,\cos\angle_{BAC}\implies$ **正弦定理 + 三角恒等变换**,$\displaystyle AB=\frac{AD}{\sin B},AC=\frac{AD}{\sin C}$.
3. 已知一角一边 $\implies$ **正弦定理** $\displaystyle a=\frac{b\sin A}{\sin B}\dots$
4. 已知 $AD$ 为角平分线 $\left[\overrightarrow{AD}=\lambda\left(\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}+\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}\right)\right]$ 与 $AB,AC\implies$ **角平分线定理 / 正弦定理 / 面积**。
5. 求内切圆半径取值范围 $\displaystyle r=\frac{2S}{a+b+c}$
例:已知 $\displaystyle c=2,C=60\degree$ 则 $\displaystyle r=\frac{\sqrt{3}}{2}\frac{ab}{a+b+2}\xlongequal{余弦定理}\frac{\sqrt{3}}{6}\frac{(a+b)^2-4}{a+b+2}=\frac{\sqrt{3}}{6}(a+b-2)=\frac{\sqrt{3}}{6}\left(\frac{c\sin A}{\sin C}+\frac{c\sin B}{\sin C}\right)=\dots$
# 立体几何
### 弧度制与面积计算
- $360\degree=2\pi\ \text{rad},\ 180\degree=\pi\ \text{rad}$
- $\displaystyle 1\degree=\frac{\pi}{180}\ \text{rad}\approx0.01745\ \text{rad},1\ \text{rad}=\left(\frac{180}{\pi}\right)\degree\approx 57.29578\degree$
- $\displaystyle x\degree=\frac{x\pi}{180}\ \text{rad},x \ \text{rad}=\left(\frac{180x}{\pi}\right)\degree$
- 圆心角大小( 弧度 ) $\displaystyle |\alpha|=\frac{l}{r}\ \ \ \ \text{}$ 圆心角大小( 角度 ) $\displaystyle n=\frac{180\cdot l}{r\pi}$
- 弧长 $l=\alpha r$,周长 $C=2r+l$,面积 $\displaystyle S=\frac{1}{2}\alpha r^2=\frac{1}{2}lr$
### 基本立体图形
- 共性:都具有顶点、底面、侧面、侧棱( 相邻侧面的公共边 )。
- 棱柱:有**两个面相互平行**,其余各面都是四边形,并且相邻两个四边形的公共边都相互平行。底面是 $n$ 边形就叫 $n$ 棱柱。斜高:侧面的高。
侧棱垂直于底面的柱叫做**直棱柱**,侧棱不垂直于底面的棱柱叫做斜柱。底面是正多边形的直棱柱叫做**正棱柱**,**底面是平行四边形的四棱柱也叫做平行六面体**。
$$\set{正方体}\in\set{正四棱柱}\in\set{长方体}\in\set{直四棱柱}$$
- 棱锥:**三棱锥又叫四面体**( 即由四个面组成的封闭图形只能是三棱锥 ),底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做**正棱锥**。
**正三棱锥 / 正四面体的三条对棱两两垂直。**
- 棱台:棱锥上部通过平行于底面的面截取上部且上下底面平行。
- 圆柱 / 圆锥 / 圆台:旋转轴称为它的轴,平行于轴的边叫做它侧面的母线。
- 欧拉公式:$V-E+F=2$,即 顶点数 Vertex $-$ 棱数 Edge $+$ 面数 Face $=2$.
| | 面数 | 棱数 | 顶点数 | 每面边数 | 每顶点棱数 | 备注 |
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| 正四面体 | $4$ | $6$ | $4$ | $3$ | $3$ | |
| 正六面体 | $6$ | $12$ | $8$ | $4$ | $3$ | 即正方体 |
| 正八面体 | $8$ | $12$ | $6$ | $3$ | $4$ | 两个正四棱锥上下叠在一起 |
| 正十二面体 | $12$ | $30$ | $20$ | $5$ | $3$ | |
| 正二十面体 | $20$ | $30$ | $12$ | $3$ | $5$ | |
### 立体图形的直观图
- 斜二测画法
$\angle xOy=90\degree\xLeftrightarrow{x\ 轴不变}\angle x'Oy'=45\degree$ 或 $135\degree,\angle x'Oz'=\angle xOz=90\degree$,$\\$ 原来平行于 **$x$ 轴 或 $z$ 轴** 的线段,在直观图中保持原长度不变,原来平行于 $y$ 轴的线段,在直观图中长度变为原来的一半。
- $\displaystyle \red{\boxed{S_{直}=\frac{\sqrt{2}}{4}S_{原},S_{原}=2\sqrt{2}S_{直}}}$
### 简单几何体的表面积和体积
下表中 $r$ 为底面半径,$l$ 为母线长,$h$ 为高,$C$ 为底面周长;特别地,台体 $S$ 与 $S'$ 分别代表上下底面面积,$r$ 与 $r'$ 同理。$\\$
棱锥侧面积计算公式中,$a$ 代表底面边长,$h'$ 为斜高。棱台侧面积计算公式中,$C'',C'$ 分别代表上下底面周长,$h''$ 代表斜高。
| 几何体 | 表面积 | 体积 | 侧面积 |
| :----: | :----------------------: | :----------------------------------------------------------------------------------------------: | :-----------------------------------: |
| 棱柱 | 围成它们的各个面面积之和 | $V=Sh$ | $S_{直棱柱侧}=Ch$ |
| 棱锥 | 围成它们的各个面面积之和 | $\displaystyle V=\frac{1}{3}Sh$ | $\displaystyle S_{正\ n\ 棱锥侧}=\frac{1}{2}nah'$ |
| 棱台 | 围成它们的各个面面积之和 | $\displaystyle V=\frac{1}{3}h(S'+\sqrt{S'S}+S)$ | $\displaystyle S_{正棱台侧}=\frac{1}{2}(C''+C')h''$ |
| 圆柱 | $S=2\pi r(r+l)$ | $V=Sh=\pi r^2h$ | $S_{圆柱侧}=2\pi rl$ |
| 圆锥 | $S=\pi r(r+l)$ | $\displaystyle V=\frac{1}{3}Sh=\frac{1}{3}\pi r^2h$ | $S_{圆锥侧}=\pi rl$ |
| 圆台 | $S=\pi(r'^2+r^2+r'l+rl)$ | $\begin{aligned}\displaystyle V&=\frac{1}{3}h(S'+\sqrt{S'S}+S)\\\displaystyle &=\frac{1}{3}\pi h(r'^2+r'r+r^2)\end{aligned}$ | $S_{圆台侧}=\pi(r+r')l$ |
| 球 | $S=4\pi r^2$ | $\displaystyle V=\frac{4}{3}\pi r^3$ | / |
- 祖暅原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
- 画展开图类问题:绳绕棱锥 / 圆锥,先求出展开图圆心角的度数( 大概率 $90\degree$ )
例 1:在正四棱锥 $O-ABCD$ 中,侧棱长均为 $4$,且相邻两条侧棱的夹角为 $30\degree$,$E,F$ 分别为线段 $OB,OC$ 上的一点,则 $AE+EF+FD$ 的最小值为 ?( $4\sqrt{2}$ )
例 2:一个圆台的上、下底面半径分别为 $5,10$,母线 $AB=20$,从圆台母线 $AB$ 的中点 $M$ 拉一条绳子绕圆台侧面转到 $A$,求绳子的最短长度( $50$ )和上底面圆周上的点到绳子的最短距离。( $4$ )
- 射影问题:三棱锥 $P-ABC$ 中,$O$ 为 $P$ 在平面 $ABC$ 内的射影,则:
| $O$ 为外心 | $O$ 为内心 | $O$ 为垂心 |
|:-:|:-:|:-:|
| $1. PA=PB=PC \\ 2. PA,PB,PC$ 与平面 $ABC$ 所成角相等 | $1. P$ 到 $\Delta ABC$ 各边距离相等 $\\ 2.$ 三侧面与底面所成二面角相等 | $1. PA\perp PB,PB\perp PC,PA\perp PC \\ 2. PA \perp BC,PB\perp AC, PC\perp AB \\$( 三组对棱互相垂直 ) |
#### 球与几何体的外接、内切问题
- 外接球:多面体 / 旋转体的顶点均在球面上,**球心到各个顶点的距离相等**,球心在旋转轴上。
注意 **球心可能在几何体外**。
- 内切球:多面体 / 旋转体的各面均与球面相切,**球心到各面的距离相等**,球心在旋转轴上。
利用**等体积法**求半径( $\displaystyle V=\frac{1}{3}S_表 r$ ),再求每个面面积,最后 $\boxed{各个棱锥的体积之和 = 多面体体积}\implies$ 内切球半径。
例 1:若三棱锥的三条侧棱两两垂直,且长度均为 $2$,则三棱锥外接球半径 $\displaystyle R=\frac{\sqrt{2^2+2^2+2^2}}{2}=\sqrt{3}$.
例 2:若三棱锥 $P-ABC$ 的三条侧棱两两垂直,$AB=\sqrt{5},BC=\sqrt{7},AC=2$,则此三棱锥的外接球的体积为 ?
$$2R=\sqrt{PA^2+PB^2+PC^2}=\sqrt{\frac{1}{2}(AC^2+AB^2+BC^2)}=2\sqrt{2}\\\implies R=\sqrt{2},V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi$$
- 球内接正三棱锥的体积最大值 $=$ 球内接正四面体的体积。
球内接正四棱锥的体积最大值 $=$ 一个底面边长 $=$ 高的正四棱锥的体积。
| 几何体 | 外接球半径 $R$ | 外接球球心 | 内切球半径 $r$ |
| :------------------------------------: | :------------------------------------------------------------------: | :----------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------: |
| 长方体 | $2R=\sqrt{a^2+b^2+c^2}$ | 体对角线的中点 | |
| 正方体 | $\displaystyle R=\frac{\sqrt{3}}{2}a$ | 体对角线的中点 | $\displaystyle r=\frac{a}{2} \\ $ 与正方体各棱相切的球 $\\$ 叫做棱切球,半径 $\displaystyle\frac{\sqrt{2}a}{2}$ |
| 直棱柱 / 圆柱 | $\displaystyle R^2=\left(\frac{h}{2}\right)^2+r^2\\ r$ 为底面外接圆半径 $\\$ 可利用正弦定理求 | 上下底面中心连线的中点 | |
| 侧棱与底面 $\\$ 垂直的锥体 | $\displaystyle R^2=\left(\frac{h}{2}\right)^2+r^2\\ r$ 为底面外接圆半径 $\\$ 可利用正弦定理求 | 过底面外接圆圆心 $\\$ 且垂直于底面的直线 $\\$ 与垂直于底面的侧棱 $\\$ 的中垂面的交点 | |
| 正棱锥 / 圆锥 | $\displaystyle R^2=(R-h)^2+r^2\\ \implies R=\frac{h^2+r^2}{2h}\\ r$ 为底面外接圆半径 $\\$ 可利用正弦定理求 | 正棱锥 / 圆锥顶点与 $\\$ 底面外心连线 / 延长线上 | |
| 正四面体 $\\$ 高 $\displaystyle\frac{\sqrt{6}a}{3}\\$ 体积 $\displaystyle\frac{\sqrt{2}}{12}a^3$ | $\displaystyle R=\frac{\sqrt{6}}{4}a \\ a$ 为其棱长 $\\$ 也可用长方体的公式 | | $\displaystyle r=\frac{\sqrt{6}}{12}a \\ a$ 为其棱长 |
- 圆台内切球半径:$r=\sqrt{r_1r_2}$
- 将四面体补形成长方体的条件( 满足其中之一即可 ):
1. 有三条棱两两垂直。
2. 四个面均是直角三角形。
3. 正四面体 $P-ABC$ 可以补形成正方体且棱长 $\displaystyle a=\frac{PA}{\sqrt{2}}$.
4. 三组对棱分别相等,长度记为 $x,y,z$,长方体边长记为 $a,b,c$,则 $\begin{cases}
x=\sqrt{a^2+b^2} \\
y=\sqrt{b^2+c^2} \\
z=\sqrt{a^2+c^2}
\end{cases}$
### 空间点、直线、平面之间的关系
- 平面的表示:用横向 / 竖向的平行四边形表示,书写方法:平面 $\alpha,\beta\dots$ 或 平面 $ABCD$,平面 $AC,BD$.
#### 四个基本事实与三个推论
- 基本事实
1. 过不在 **同一直线上** 的三个点,有且只有一个平面。即**不共线的三点确定一个平面**。
一条直线与直线外一点也能确定一个平面。
在同一平面内,$n$ 条直线最多把平面划分为 $\displaystyle 1+\frac{n(n-1)}{2}$ 份;在空间内,$n$ 个平面最多把空间分为 $\displaystyle \frac{n^3+5n+6}{6}$ 份。
相交于同一点的 $n$ 条直线最多可以确定 $\begin{cases}\displaystyle\frac{n(n-1)}{2}\ 个平面 & 任意\ 3\ 条不共面 \\ \displaystyle\frac{(n-3)(n-4)}{2}\ 个平面 & 有\ 3\ 条不共面 \end{cases}$
2. 如果一条直线上的两个点在同一平面内,那么这条直线在这个平面内。即:
直线 $l$ 在 $\alpha$ 内 $\xLeftrightarrow{}l\subset\alpha\ \ \ \ \text{}$ 直线 $l$ 不在 $\alpha$ 内 $\xLeftrightarrow{}l\not\subset\alpha$
基本事实 2 用符号表示为:$A\in l,B\in l$ 且 $A\in\alpha,B\in\alpha\implies l\subset\alpha$
3. 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
平面 $\alpha$ 与 $\beta$ 相交于直线 $l$,记作 $\alpha\cap\beta=l$.
基本事实 3 用符号表示为:$P\in\alpha$ 且 $P\in\beta\implies\alpha\cap\beta=l$ 且 $P\in l$
4. 平行于同一条直线的两条直线平行。( 平行线的传递性 )
注意表示 **点** 在 直线 / 平面 内用 $\in$,表示 **直线** 在 平面 内用 $\subset$.
- 推论( 基本事实 1 + 2 + 两点确定一条直线 )
1. 经过一条直线和这条直线外一点,有且只有一个平面。
2. 经过两条相交直线,有且只有一个平面。
3. 经过两条平行直线,有且只有一个平面。
#### 空间点、直线、平面之间的位置关系
$$直线与直线\begin{cases}共面直线\begin{cases}相交直线:在同一平面内,有且只有一个公共点 \\ 平行直线:在同一平面内,没有公共点\end{cases} \\ 异面直线:不同在任何一个平面内,没有公共点\end{cases}$$
$$直线与平面\begin{cases}直线在平面内 \ \ \ \ \ \ \ \ 有无数个公共点 \\ \begin{rcases}直线与平面相交 & 有且只有一个公共点 \\ 直线与平面平行 & 没有公共点\end{rcases} 直线在平面外 \end{cases}$$
$$直线\ a\ 与平面\ \alpha\ 相交于点\ A,记作a\cap\alpha=A\ \ \ \ \ 直线\ a\ 与平面\ \alpha\ 平行,记作\ a\parallel\alpha$$
$$平面与平面\begin{cases}两个平面平行 & 没有公共点 \\ 两个平面相交 & 有一条公共直线\end{cases}$$
$$平面\ \alpha\ 与平面\ \beta\ 平行,记作\ \alpha\parallel\beta$$
#### 证明共面、共线、共点
1. 证明点、线共面:证明直线平行 / 相交;确定一个辅助平面;反证法。
2. 证明三点共线:先找 $2$ 个平面,证明这 $3$ 点都是 $2$ 个平面公共点 / 其中 $2$ 点确定 $1$ 条直线,证另一点也在直线上。
3. 证明三线共点:先证明两条直线交于一点,再证明第三条直线经过这个点或交点在第三条直线上。
注意梯形两腰必交于一点;在空间中,不能用两组对边分别相等证明平行四边形。
例题:已知正方体 $ABCD-A_1B_1C_1D_1$,$M,N$ 为棱 $A_1B_1,B_1C_1$ 中点,求证:$\\ \ \ \ \ \ (1)$ 直线 $AM,CN$ 共面; $\\ \ \ \ \ \ (2)$ 直线 $D_1B$ 和 $CC_1$ 是异面直线。
$pf:(1)AA_1 \parallel CC_1,AA_1=CC_1\implies$ 四边形 $ACC_1A_1$ 是平行四边形。
$\ \ \ \ \ \ AC\parallel A_1C_1\parallel MN \implies$ 直线 $AM,CN$ 共面。
$\ \ \ \ \ \ \ (2)$ 反证法,假设四点共面于 $\alpha$,则 $B,C,C_1$ 可以确定一个平面 $BC_1$,这两个平面重合,又因为 $D_1B \sub $ 平面 $BC_1$,所以 $D_1\in$ 平面 $BC_1$,与 $D_1\notin$ 平面 $BC_1$ 矛盾,故原假设错误。
### 空间直线、平面的平行
1. 等角定理:如果空间中两个角的两条边分别对应平行,那么两个角相等或互补。
2. 直线与平面平行的判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
用符号表示:$a\not\subset\alpha,b\subset\alpha,a\parallel b\implies a\parallel\alpha$
3. 直线与平面平行的性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行。
用符号表示:$a\parallel\alpha,\alpha\cap\beta=b,a\subset\beta\implies a\parallel b$
4. 平面与平面平行的判定定理:如果一个平面内的 **两条相交直线** 与另一个平面平行,那么这两个平面平行。
用符号表示:$a\subset\beta,b\subset\beta,a\cap b=P,a\parallel\alpha,b\parallel\alpha\implies\alpha\parallel\beta$
5. 平面与平面平行的性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行。
用符号表示:$\alpha\parallel\beta,\alpha\cap\gamma=a,\beta\cap\gamma=b\implies a\parallel b$
可简记为:线线平行 $\iff$ 线面平行 $\implies$ 面面平行 $\implies$ 线线平行,恰好形成一个循环。
### 空间直线、平面的垂直
- 直线与平面垂直的判定定理:如果一条直线与一个平面内的 **两条相交直线** 垂直,那么该直线与此平面垂直。
用符号表示:$m\subset\alpha,n\subset\alpha,m\cap n=P,l\perp m,l\perp n\implies l\perp\alpha$
- 直线与平面垂直的性质定理:垂直于同一个平面的两直线平行。
- 平面与平面垂直的判定定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直。
用符号表示:$a\subset\alpha,a\perp\beta\implies\alpha\perp\beta$
- 平面与平面垂直的性质定理:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直。
### 空间直线、平面的平行
1. 三棱锥 $P-ABC$ 中,$D,E$ 分别是 $PB,BC$ 中点,点 $F$ 在线段 $AC$ 上,且满足 $AD \parallel $ 平面 $PEF$,则 $\displaystyle\frac{AF}{FC}=$ ?
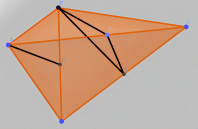
解析:连接 $CD$,交 $PE$ 于点 $G$,连接 $FG$,如图所示。
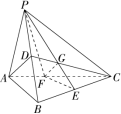
$AD \parallel$ 平面 $PEF$, 平面 $PEF\ \cap$ 平面 $ADC=FG\implies AD \parallel FG$
$D,E$ 分别是 $PB,BC$ 中点 $\implies G$ 是 $\Delta PBC$ **重心**,$\displaystyle\frac{AF}{FC}=\frac{DG}{GC}=\frac{1}{2}$.
---
2. 长方体 $ABCD-A_1B_1C_1D_1,AB=BC,E$ 是 $AB$ 上靠近 $B$ 的三等分点,$F$ 是 $A_1D_1$ 中点,$\\ O$ 为直线 $DB_1$ 与平面 $EFC$ 交点,$\displaystyle\frac{DO}{OB_1}=$ ?
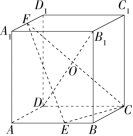
解析:连接 $BD,B_1D_1,BD \cap CE=M$,$\\$ 设平面 $CEF$ 与平面 $A_1B_1C_1D_1$ 的交线交 $C_1D_1,B_1D_1,A_1B_1$ 分别于点 $P,N,Q$,如图所示。
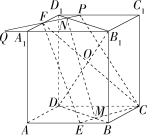
$\displaystyle CE \parallel PQ \implies \angle PFD_1=\angle BCE \implies \mathrm{Rt}\Delta PFD_1 \sim \mathrm{Rt}\Delta ECB,\frac{PD_1}{FD_1}=\frac{EB}{BC}=\frac{1}{3}$
$\displaystyle QA_1=PD_1=\frac{1}{3}FD_1=\frac{1}{6}A_1B_1\implies\frac{B_1N}{ND_1}=\frac{B_1Q}{PD_1}=7$
$\displaystyle \frac{DM}{MB}=\frac{DC}{EB}=3\implies DM=\frac{3}{4}BD\implies\frac{DO}{OB_1}=\frac{DM}{NB_1}=\frac{6}{7}$
---
3. 四棱锥 $P-ABCD$ 的底面是边长为 $1$ 的正方形,$E$ 是 $PD$ 上一点满足 $PE=3ED$,若 $\overrightarrow{PF}=\lambda\overrightarrow{PC}$ 且 $BF\parallel$ 平面 $AEC$,则 $\lambda=$ ?
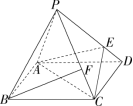
解析:连接 $BD$ 交 $AC$ 于点 $O$,连接 $OE$,在 $PD$ 上取一点 $G$ 使得 $GE=ED$.
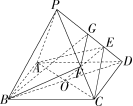
在 $\Delta BGD$ 中 $EO$ 为其中位线 $\implies BG\parallel$ 平面 $AEC\implies$ 平面 $BFG\ \parallel$ 平面 $AEC$.
$\displaystyle\frac{PF}{FC}=\frac{PG}{GE}=2,\lambda=\frac{2}{3}$
---
4. 在长方体 $ABCD-A_1B_1C_1D_1$ 中,$AD=DD_1=1,AB=\sqrt{3},E,F,G$ 分别是 $AB,BC,C_1D_1$ 的中点,点 $P$ 在平面 $ABCD$ 内,若直线 $D_1P\ \parallel$ 平面 $EFG$,则点 $D_1$ 与满足题意的点 $P$ 构成的平面截长方体所得的截面的面积为 ?
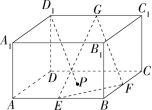
解析:
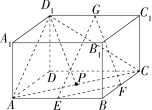
只需证明点 $D_1$ 与满足题意的点 $P$ 构成的平面 $D_1AC$ 平行于平面 $EFG$ 即可,答案即为 $\displaystyle S_{\Delta D_1AC}=\frac{\sqrt{7}}{2}$.
---
5. 如图,三棱柱 $ABC-A_1B_1C_1$ 中,$D$ 是 $B_1C_1$ 中点,$E$ 是 $A_1C_1$ 上一点满足 $A_1B\parallel$ 平面 $B_1DE$,则 $\displaystyle\frac{A_1E}{EC_1}=$ ?
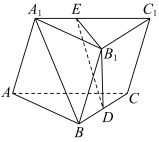
解析:连接 $BC_1$ 交 $B_1D$ 于 $F$,易证 $\displaystyle\Delta A_1BC_1 \sim \Delta EFC_1,\frac{A_1E}{EC_1}=\frac{BF}{FC_1}=\frac{BD}{B_1C}=\frac{1}{2}$.
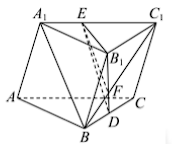
### 空间直线、平面的垂直
1. 如图,$P$ 是 $\Delta ABC$ 所在平面外一点,$PA\perp$ 平面 $ABC,\angle ABC=90\degree,AE\perp PB$ 于 $E,AF\perp PC$ 于 $F.\\$ 求证:$(1)\ BC\perp$ 平面 $PAB \\ \ \ \ \ \ \ \ \ \ \ (2)\ AE\perp$ 平面 $PBC \\ \ \ \ \ \ \ \ \ \ \ (3)\ PC\perp$ 平面 $AEF$
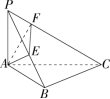
解析:$(1)\ \angle ABC=90\degree\implies BC\perp AB\ \ \ \ \ \ \ PA\perp$ 平面 $ABC\implies BC\perp PA\\ \ \ \ \ \ \ \ \ \ \ (2)\ BC\perp$ 平面 $PAB\implies AE\perp BC\\ \ \ \ \ \ \ \ \ \ \ (3)\ AE\perp$ 平面 $PBC\implies PC\perp AE$
### 定理 & 二级结论
- 速求内切球:若某一**几何体**的表面积为 $S$,体积为 $V$,内切球半径为 $r$,则满足 $\displaystyle \red{\boxed{V=\frac{1}{3}Sr}}$
- 速求外接球:$\text{A.L.Crelle}$ 公式:给定任意一个**四面体** $A-BCD$,三组对棱长分别为 $a,a_1,b,b_1,c,c_1$,设 $\displaystyle p=\frac{1}{2}(aa_1+bb_1+cc_1)$,则体积 $V$ 和外接球半径 $R$ 满足
$$6RV=\sqrt{p(p-aa_1)(p-bb_1)(p-cc_1)}$$
- 三垂线定理:如果平面内的一条直线与平面外的一条斜线在该平面内的射影垂直,那么它也和这条斜线垂直。
逆定理:如果平面内一直线和这个平面外的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直。
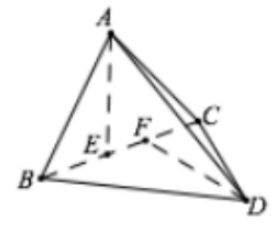
- 空间第一余弦定理:如图,$AE\perp BC,DF\perp BC$,则二面角 $A-BC-D$ 的大小 $\theta$ 满足
$$\red{\boxed{\cos\theta=\frac{AE^2+EF^2+FD^2-AD^2}{2AE\cdot FD}}}$$
- 斯坦纳定理( maybe? ):空间第二余弦定理:空间中两直线 $AB,CD$ 的夹角 $\theta$ 满足 $$\red{\boxed{\cos\theta=\frac{|AD^2+BC^2-AC^2-BD^2|}{2AB\cdot CD}}}$$
证明:
$\displaystyle\begin{aligned}\overrightarrow{AC}\cdot\overrightarrow{BD}&=\overrightarrow{AC}\cdot(\overrightarrow{AD}-\overrightarrow{AB})=|\overrightarrow{AC}||\overrightarrow{AD}|\cos\angle_{CAD}-|\overrightarrow{AC}||\overrightarrow{AB}|\cos\angle_{CAB}\\&=AC\cdot AD\cdot \frac{AC^2+AD^2-CD^2}{2AC\cdot AD}-AC\cdot AB\cdot\frac{AC^2+AB^2-BC^2}{2AC\cdot AB}\\&=\frac{AD^2+CB^2-AB^2-CD^2}{2}\end{aligned}$
- 三面角公式求二面角:已知 $\angle_{APB}=\theta_1,\angle_{BPC}=\theta_2,\angle_{APC}=\theta_3$,则二面角 $A-PB-C$ 的余弦值为
$$\red{\boxed{\cos\theta=\frac{\cos\theta_3-\cos\theta_1\cos\theta_2}{\sin\theta_1\sin\theta_2}=\frac{\cos\angle_{APC}-\cos\angle_{APB}\cdot\cos\angle_{BPC} }{\sin\angle_{APB}\cdot\sin\angle_{BPC} }}}$$
注意三个角度在公式中分布特点,$\theta_3$ 是二面角 $A-PB-C$ 的对角,而 $\theta_1,\theta_2$ 就是二面角 $A-PB-C$ 的两个邻角。
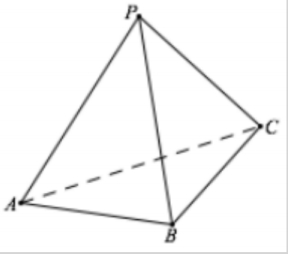
- 三正弦定理:二面角 $M-AB-N$ 的度数为 $\alpha$,平面 $M$ 上有一射线 $AC$ 与 $AB$ 所成角为 $\beta$,与平面 $N$ 所成角为 $\gamma$,则 $\sin\gamma=\sin\alpha\sin\beta$.
- 三余弦定理 / 最小角定理:设 $A$ 为平面 $\alpha$ 上一点,过点 $A$ 的斜线 $AO$ 在平面 $\alpha$ 上的射影为 $AB$,$AC$ 为平面 $\alpha$ 内的一条直线,那么有 $\cos\angle OAC=\cos\angle BAC\times\cos\angle OAB$.
证明:$\displaystyle\cos\angle OAC=\frac{AC}{AO}\ \ \ \ \cos\angle BAC=\frac{AC}{AB}\ \ \ \ \cos\angle OAB=\frac{AB}{AO}$
即**斜线与射影所成的角是斜线与平面内的任何直线所成的角中最小的角**。
- 异面直线段 $AB=a,CD=b$,它们之间的距离为 $d$,夹角为 $\theta$,则 $\displaystyle V_{A-BCD}=\frac{1}{6}abd\sin\theta$.
- 面积余弦定理:$\Delta ABC$ 在平面 $\alpha$ 内的射影为 $\Delta ABO$,记 $\Delta ABC$ 所在平面与 $\alpha$ 所称的锐二面角为 $\theta$,则 $S_{\Delta ABO}=\cos\theta S_{\Delta ABC}$.
### 翻折问题
- 不在同一平面的两点路径问题的翻折只能以折点所在直线翻折。
例:长方体 $ABCD-A_1B_1C_1D_1$ 中,$AB=1,AD=2,AA_1=3,P$ 是线段 $B_1C$ 上一动点,求 $AP+PD_1$ 的最小值 ?
画出直观图后,应将平面 $AB_1C$ 和平面 $B_1CD_1$ 翻折到同一平面上,显然 $AB_1D_1C$ 是平行四边形。
根据平行四边形中对角线平分和 $=$ 四条边平方和可得 $(AP+PD_1)_{\min}=AD_1=\sqrt{17}$.
- 注意**分类讨论**
例:直三棱柱 $ABC-A_1B_1C_1$ 中,$E,F$ 分别为 $AA_1,C_1B_1$ 的中点,沿棱柱的表面从 $E$ 到 $F$ 两点的最短路径的长度是 ?
分三类讨论:
1. 沿 $BB_1$ 展开,算得 $\displaystyle EF=\frac{\sqrt{22}}{2}$.
2. 沿 $A_1C_1$ 展开,算得 $\displaystyle EF=\frac{3\sqrt{2}}{2}$.
3. 沿 $A_1B_1$ 展开,算得 $\displaystyle EF=\sqrt{\frac{7}{2}+\sqrt{2}}$.
于是 $\displaystyle EF_{\min}=\frac{3\sqrt{2}}{2}$.
### 截面问题
1. 求过圆锥顶点的截面面积最大值:记轴截面顶角为 $\theta$,$\displaystyle\sin\theta=\frac{r}{l}$. $\begin{cases}\theta>\frac{\pi}{2},S_{\max}=\frac{1}{2}l^2\sin\theta\implies\frac{1}{2}l^2 \\ \theta\leq\frac{\pi}{2},S_{\max}=\ 轴截面面积 \end{cases}$
2. 正方体棱长为 $1$,每条棱所在直线与平面 $\alpha$ 所称角相等,则 $\alpha$ 截此正方体所得截面面积最大值 ?
注意正方体截面可以是 $3,4,5,6$ 边形,最大面积是 $\displaystyle\frac{3\sqrt{3}}{4}$.
例题:在棱长为 $2$ 的正方体 $ABCD-A_1B_1C_1D_1$ 中,$E$ 为棱 $AA_1$ 中点,点 $F$ 在 $A_1B_1$ 上且满足 $\overrightarrow{A_1F}=\lambda\overrightarrow{A_1B_1}$,以下正确的有( $\text{ACD}$ )
$\text{A.}$ 当 $\lambda=0$ 时,$AC_1\perp$ 平面 $BDF$。
$\text{B.}$ $\forall\lambda\in[0,1],V_{F-BDE}$ 不变。
$\text{C.}$ $\exist\lambda\in[0,1]$,直线 $AC$ 与平面 $BDF$ 所成角为 $\displaystyle\frac{\pi}{3}$.
$\text{D.}$ 当 $\displaystyle\lambda=\frac{2}{3}$ 时,平面 $BDF$ 截正方体外接球所得截面面积为 $\displaystyle\frac{56}{19}\pi$.
选项 $\text{D}$ 解析:
首先把平面补全为 $BDGF$,其中 $G$ 为棱 $A_1D_1$ 上靠近 $D_1$ 的三等分点。
连接 $A_1C_1$ 与 $GF,B_1D_1$ 分别交于点 $P,Q$,连接 $AC$ 与 $BD$ 交于点 $E$,连接 $PE$。
显然正方体外接球球心 $O$ 为线段 $QE$ 中点,记截面所在圆的圆心为 $O_1$,则 $OO_1\perp$ 平面 $BDF$。
因为 $P,E$ 均为对角线上的点,所以 $O_1$ 在线段 $PE$ 上。
于是 $\text{Rt}\Delta PQE \sim \text{Rt} \Delta OO_1E$,可算得 $\displaystyle PQ=\frac{\sqrt{2}}{3},PE=\frac{\sqrt{38}}{3},OO_1=\frac{1}{\sqrt{19}}$.
正方体外接球半径 $R=\sqrt{3}$,截面圆半径 $\displaystyle r=\sqrt{R^2-OO_1^2}=\frac{2\sqrt{266}}{19},S=\pi r^2=\frac{56}{19}\pi$.
### 其他好题
已知三棱锥 $P-ABC$ 中,$PA\perp $ 平面 $ABC$,且 $PA=BC=1,AB+AC=2$,若二面角 $P-BC-A$ 的平面角与 $\angle BAC$ 的大小相等,则三棱锥 $P-ABC$ 的外接球表面积为 ?
注意 $AB+AC=2$ 实际上给出了一个椭圆,那么只需利用椭圆焦点三角形面积公式求角度即可。答案是 $\displaystyle\frac{41}{16}\pi$.
# 空间向量
基本运算同平面向量。
- $\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$ 且 $x+y+z=1,A,B,C$ 不共线,$O\not\subset$ 平面 $ABC\implies A,P,B,C$ 四点共面。
证明:
$$\overrightarrow{AP}=m\overrightarrow{AC}+n\overrightarrow{AB}=\overrightarrow{OP}-\overrightarrow{OA}=m(\overrightarrow{OC}-\overrightarrow{OA})+n(\overrightarrow{OB}-\overrightarrow{OA})=(1-m-n)\overrightarrow{OA}+n\overrightarrow{OB}+m\overrightarrow{OC}$$
- 若 $\Delta ABC$ 重心为 $G$,$O$ 为 $\Delta ABC$ 平面外一点,则 $\displaystyle\overrightarrow{OG}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$.
- 法向量:垂直于平面 $\alpha$ 的向量,有无数多个;怎么求:设法向量为 $(x,y,z)$,求出平面内两个向量的坐标表示,点乘列方程组求。
- 速求法向量:已知平面 $\alpha$ 上的两个向量 $\overrightarrow{a}=(x_1,y_1,z_1),\overrightarrow{b}=(x_2,y_2,z_2)$,则平面的一个法向量为 $\left(\begin{vmatrix}y_1 & z_1 \\ y_2 & z_2\end{vmatrix},\begin{vmatrix}z_1 & x_1 \\ z_2 & x_2\end{vmatrix},\begin{vmatrix}x_1 & y_1 \\ x_2 & y_2\end{vmatrix}\right)=(y_1z_2-y_2z_1,z_1x_2-z_2x_1,x_1y_2-x_2y_1)$.
相当于求向量叉乘。
- 对称问题
$(a,b,c)$ 关于什么对称,什么就不变。
| 原点 $O$ | $x$ 轴 | $y$ 轴 | $z$ 轴 | $Oxy$ 平面 | $Oyz$ 平面 | $Oxz$ 平面 |
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| $(-a,-b,-c)$ | $(a,-b,-c)$ | $(-a,b,-c)$ | $(-a,-b,c)$ | $(a,b,-c)$ | $(-a,b,c)$ | $(a,-b,c)$ |
### 平面方程
- 过 $P(x_0,y_0,z_0)$ 且法向量 $\overrightarrow{m}=(A,B,C)$ 的平面方程为 $A(x-x_0)+B(y-y_0)+C(z-z_0)=0$.
- 过 $P(x_0,y_0,z_0)$ 且方向向量 $\overrightarrow{n}=(u,v,w)$ 的直线 $l$ 的方程为 $\displaystyle\frac{x-x_0}{u}=\frac{y-y_0}{v}=\frac{z-z_0}{w}\ (uvw\neq 0)$.
### 用空间向量研究距离、夹角问题
1. 点线距 —— 求点 $A$ 到直线 $BC$ 的距离。
$\displaystyle\overrightarrow{a}=\overrightarrow{BA},\ \overrightarrow{u}=\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|},\ \red{\boxed{d=\sqrt{\overrightarrow{a}^2-(\overrightarrow{a}\cdot\overrightarrow{u})^2}}}$
2. 点面距 / 线面距 / 面面距 —— 求点 $A$ 到平面 $BCD$ 的距离。
1. 等体积法,$V_{A-BCD}=V_{B-ACD}=V_{C-ABD}=V_{D-ABC}$
2. 求平面 $BCD$ 的法向量 $\displaystyle\overrightarrow{n},\red{\boxed{d=\frac{|\overrightarrow{BA}\cdot\overrightarrow{n}|}{|\overrightarrow{n}|}}}$
3. $A(x_0,y_0,z_0)$,平面的解析式 $\displaystyle Ax+By+Cz+D=0,d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$
3. 线线角 —— 求 $AB,CD$ 夹角 $\theta$
1. 求出它们的方向向量 $\overrightarrow{u},\overrightarrow{v}$,则 $\displaystyle\red{\boxed{\cos\theta=\frac{\overrightarrow{AB}\cdot\overrightarrow{CD}}{|\overrightarrow{AB}||\overrightarrow{CD}|}=\frac{|\overrightarrow{u}\cdot\overrightarrow{v}|}{|\overrightarrow{u}||\overrightarrow{v}|}}}$
2. 空间第二余弦定理 $\displaystyle\cos\theta=\frac{|AD^2+BC^2-AC^2-BD^2|}{2AB\cdot CD}$
4. 线面角 —— $\displaystyle\red{\boxed{\sin\theta=\frac{|\overrightarrow{u}\cdot\overrightarrow{n}|}{|\overrightarrow{u}||\overrightarrow{n}|}}}$ ,较难做的题目亦可用等体积法。
5. 二面角 —— $\displaystyle\red{\boxed{\cos\theta=\frac{|\overrightarrow{n_1}\cdot\overrightarrow{n_2}|}{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}}$
| 两直线所成角 | 异面直线所成角 | 线面角 | 平面与平面的夹角 | 二面角 | 向量夹角 | ( 直线 )倾斜角 |
|:--:|:--:|:--:|:--:|:--:|:--:|:--:|
| $\displaystyle\left[0,\frac{\pi}{2}\right]$ | $\displaystyle\left(0,\frac{\pi}{2}\right]$ | $\displaystyle\left[0,\frac{\pi}{2}\right]$ | $\displaystyle\left[0,\frac{\pi}{2}\right]$ | $[0,\pi]$ | $[0,\pi]$ | $[0,\pi)$ |
### 向量叉乘
- 若 $\overrightarrow{a}=a_x\overrightarrow{i}+a_y\overrightarrow{j}+a_z\overrightarrow{k}$,$\overrightarrow{b}=b_x\overrightarrow{i}+b_y\overrightarrow{j}+b_z\overrightarrow{k}$,则 $\overrightarrow{c}=\overrightarrow{a}\times\overrightarrow{b}=\begin{vmatrix}
\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\
a_x & a_y & a_z \\
b_x & b_y & b_z
\end{vmatrix}$
叉乘的结果是向量,该向量的模值与 $\overrightarrow{a},\overrightarrow{b}$ 构成的平行四边形面积相等,即 $|\overrightarrow{a}\times\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}||\sin\theta|=x_1y_2-x_2y_1$.
该向量的方向垂直于 $\overrightarrow{a},\overrightarrow{b}$ 构成的平面,用右手螺旋性质确定。
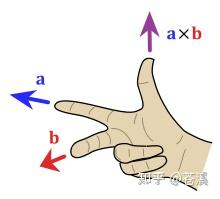
运算特性:$\begin{cases}
\overrightarrow{a}\times\overrightarrow{b}=-\overrightarrow{b}\times\overrightarrow{a} \\
\overrightarrow{a}\times\overrightarrow{a}=\overrightarrow{0} \\
\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\times\overrightarrow{b}+\overrightarrow{a}\times\overrightarrow{c} \\
(\overrightarrow{a}\times\overrightarrow{b})\times\overrightarrow{c}=(\overrightarrow{a}\cdot\overrightarrow{c})\overrightarrow{b}-(\overrightarrow{b}\cdot\overrightarrow{c})\overrightarrow{a}
\end{cases}$
# 解析几何
## 直线和圆的方程
倾斜角:$x$ 轴正向与直线 $l$ 向上的方向之间所成的角 $\alpha$.
斜率:$\displaystyle k=\tan\alpha=\frac{y_2-y_1}{x_2-x_1}$.
$$l_1\perp l_2\implies k_1\cdot k_2=-1,|\alpha_1-\alpha_2|=90\degree$$
直线的一般式方程:$Ax+By+C=0\implies$ 斜截式方程 $\displaystyle y=-\frac{A}{B}x-\frac{C}{B}\implies$ 该直线的方向向量 $\overrightarrow{u}=(B,-A)$,法向量 $\overrightarrow{n}=(A,B)$.
点到直线距离公式:$\displaystyle\red{\boxed{d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}}}$
两条平行直线之间距离:$\displaystyle\red{\boxed{d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}}}$
两条平行直线之间的铅锤高差:$\displaystyle\red{\boxed{h=\frac{|C_1-C_2|}{|B|}}}$
弦长公式:若 $y=kx+b$,则直线上两点间距离为 $$\red{\boxed{|AB|=\sqrt{1+k^2}|x_1-x_2|=\sqrt{1+\frac{1}{k^2}}|y_1-y_2|}}$$
### 对称问题
1. 点 $(x,y)$ 关于 $(a,b)$ 对称点为 $(2a-x,2b-y)$.
2. 直线 $l:Ax+By+C=0$ 关于点 $(x_0,y_0)$ 的对称直线 $A(2x_0-x)+B(2y_0-y)+C=0$.
3. 点关于直线的对称点通过设中点来列方程求。
### 圆
圆的标准方程:$(x-a)^2+(y-b)^2=r^2$.
圆的一般方程:$x^2+y^2+Dx+Ey+F=0$,其中 $D^2+E^2-4F>0$,化为标准形式为
$$\boxed{\left(x+\frac{D}{2}\right)^2+\left(y+\frac{E}{2}\right)^2=\frac{D^2+E^2-4F}{4}}$$
| 两圆关系 | 内含 | 内切 | 相交 | 外切 | 相离 |
|:-:|:-:|:-:|:-:|:-:|:-:|
| 公切线数 | $0$ | $1$ | $2$ | $3$ | $4$ |
以 $(x_1,y_1),(x_2,y_2)$ 为直径的两端点的圆的方程:
$$\left(x-\frac{x_1+x_2}{2}\right)^2+\left(y-\frac{y_1+y_2}{2}\right)^2=\left(\frac{x_1+x_2}{2}\right)^2+\left(\frac{y_1+y_2}{2}\right)^2$$
化简为
$$\red{\boxed{(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0}}$$
过圆 $(x-a)^2+(y-b)^2=r^2$ 上一点 $(x_0,y_0)$ 的切线方程:( 直接设斜率 $k$ 得证 )
$$\red{\boxed{(x-a)(x_0-a)+(y-b)(y_0-b)=r^2}}$$
过圆 $x^2+y^2+Dx+Ey+F=0\ (D^2+E^2-4F>0)$ 上一点 $(x_0,y_0)$ 的切线方程为( 极点极线 )
$$x_0x+y_0y+\frac{D(x+x_0)}{2}+\frac{E(y+y_0)}{2}+F=0$$
设点 $M(x_0,y_0)$ 是圆 $O:(x-a)^2+(y-b)^2=r^2$ 外一点,过点 $M$ 作圆的两条切线,切点分别为 $A,B$,则直线 $AB$ 的方程为
$$\red{\boxed{(x-a)(x_0-a)+(y-b)(y_0-b)=r^2}}$$
证明:$O,M,A,B$ 四点共圆,求出这个圆的方程,然后与圆 $O$ 的方程相减即可。
经过圆外一点 $P(x_0,y_0)$ 引圆的两条切线,则
| 圆的方程 | 切线长公式 |
|:-:|:-:|
| $(x-a)^2+(y-b)^2=r^2$ | $\sqrt{(x_0-a)^2+(y_0-b)^2-r^2}$ |
| $x^2+y^2+Dx+Ey+F=0 \\ (D^2+E^2-4F>0)$ | $\sqrt{x_0^2+y_0^2+Dx_0+Ey_0+F}$ |
两圆相交时,**两圆方程做差得到公共弦所在直线的方程**,即
$$D_1x+E_1y+F_1-(D_2x+E_2y+F_2)=0$$
参数方程:$P(x,y)$ 满足 $\begin{cases}x=a+r\cos\theta \\ y=b+r\sin\theta\end{cases}(r>0)$ 的轨迹为 $(x-a)^2+(y-b)^2=r^2$.
例题:圆 $O:x^2+y^2=16$,$P$ 在 $x=8$ 上运动,过 $P$ 作 $PA,PB$ 两切线,求 $AB$ 定点 ?
设 $P(8,t)$,有 $O,A,P,B$ 四点共圆,方程为 $\displaystyle(x-4)^2+\left(y-\frac{t}{2}\right)^2=16+\frac{t^2}{4}$,与 $x^2+y^2=16$ 相减得到定点 $(2,0)$.
阿氏圆:平面上 $A(a,0)$,则动点 $P(x,y)$ 满足 $\displaystyle\frac{PA}{PO}=k(k>0,k\neq 1)$ 时 $P$ 的轨迹是圆。
例题:$x^2+y^2=4,A(3,0),B(0,4)$,$P$ 为圆上一点,求 $2PA+PB$ 最小值 ?
式子变成 $\displaystyle 2\left(PA+\frac{1}{2}PB\right)$,设 $C(0,1)$,相似得到 $\displaystyle\frac{1}{2}PB=PC$,得到答案 $2\sqrt{10}$.
## 圆锥曲线的方程
### 椭圆
- 概念:平面内到两个焦点 $F_1,F_2$ 的距离的和等于常数( 大于 $|F_1F_2|$ )的点的轨迹叫做椭圆。
集合 $P=\set{M||MF_1|+|MF_2|=2a},|F_1F_2|=2c$
| 标准方程 | $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\\$ 焦点在 $x$ 轴上 | $\displaystyle\frac{x^2}{b^2}+\frac{y^2}{a^2}=1(a>b>0)\\$ 焦点在 $y$ 轴上 |
|:-:|:-:|:-:|
| 顶点坐标 | $(\pm a,0),(0,\pm b)$ | $(\pm b,0),(0,\pm a)$ |
| 对称轴 | $x$ 轴、$y$ 轴 | $x$ 轴、$y$ 轴 |
| 焦点坐标 | $(\pm c,0)$ | $(0,\pm c)$ |
| 准线 | $\red{\boxed{\displaystyle x=\pm\frac{a^2}{c}}}$ | $\displaystyle y=\pm\frac{a^2}{c}$ |
- $\boxed{c^2=a^2-b^2}$,离心率 $\boxed{e=\frac{c}{a}}\ (0<e<1)$
$e$ 越趋近于 $1$ ,椭圆越扁;否则越圆。
椭圆的面积:$S=\pi ab$( $a,b$ 分别为长半轴、短半轴的长 )
证明:在第一象限令 $x=a\sin t,y=b\cos t$,则 $$S=4\int_0^{\frac{\pi}{2}}ab\cos^2t\ \mathrm{dt}=4ab\int_0^{\frac{\pi}{2}}\frac{1+\cos 2t}{2}\ \mathrm{dt}=2ab\left(t+\frac{1}{2}\sin 2t\right)|_0^{\frac{\pi}{2}}=\pi ab$$
准线:椭圆上一点 $M(x,y)$ 与顶点 $F(\pm c,0)$ 的距离和它到该直线的距离比是常数 $e$.( 椭圆的**第二定义** )
椭圆的**第三定义**:设 $A(-a,0),B(a,0),P(x,y)\in C$,则 $\boxed{k_{AP}\cdot k_{BP}=-\frac{b^2}{a^2}=e^2-1}$
#### 椭圆焦点三角形的性质
椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上异于左、右顶点的点 $P(x_0,y_0)$ 与两焦点 $F_1,F_2$ 构成的 $\Delta PF_1F_2$ 叫做焦点三角形。
以下记 $\angle F_1PF_2=\theta$.
1. 周长 $C=2(a+c)$.
2. 面积 $\red{\boxed{S=b^2\tan\frac{\theta}{2}=c|y_0|=\frac{1}{2}|PF_1||PF_2|\sin\theta=r(a+c)}}$,$r$ 为焦点三角形的内接圆半径,当 $y_0=b$ 即点 $P$ 的位置为短轴端点时取最大值,且 $\cos\theta\geq 1-2e^2$.
证明:由余弦定理,
$$|F_1F_2|^2=|PF_1|^2+|PF_2|^2-2|PF_1||PF_2|\cos\theta=(|PF_1|+|PF_2|)^2-2(1+\cos\theta)\cdot|PF_1||PF_2|$$
因为 $|PF_1|+|PF_2|=2a,|F_1F_2|=2c$,所以 $\displaystyle|PF_1||PF_2|=\frac{2a^2-2c^2}{1+\cos\theta}=\frac{2b^2}{1+\cos\theta}$.
又因为 $\displaystyle\boxed{\frac{\sin\theta}{1+\cos\theta}}=\frac{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}{1+(2\cos^2\frac{\theta}{2}-1)}=\frac{\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}}=\boxed{\tan\frac{\theta}{2}}$.
因此 $\displaystyle S=\frac{1}{2}|PF_1||PF_2|\sin\theta=\frac{b^2\sin\theta}{1+\cos\theta}=b^2\tan\frac{\theta}{2}$.
3. $|PF_1|\cdot|PF_2|\in (b^2,a^2]$.
4. 设 $\angle PF_1F_2=\alpha,PF_2F_1=\beta$,则 $\displaystyle\red{\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\alpha+\sin\beta}}=\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}}}$. ( 证明:正弦定理 )
5. 若焦点三角形内切圆的圆心为 $I$,延长 $PI$ 交 $F_1F_2$ 于点 $Q$,则
$$\frac{|PI|}{|IQ|}=\frac{|PF_1|}{|F_1Q|}=\frac{|PF_2|}{|F_2Q|}=\frac{|PF_1|+|PF_2|}{|F_1Q|+|F_2Q|}=\frac{2a}{2c}=\frac{1}{e}$$
#### 椭圆的其它几何性质
以下均研究椭圆 $\displaystyle\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的性质。
- 通径:过 $\Gamma$ 的焦点作垂直于长轴的直线,该直线被椭圆截得的弦叫做通径,其长度为 $\displaystyle\frac{2b^2}{a}$.
若不垂直,则其长度为 $\displaystyle|PP_0|=\frac{\frac{2b^2}{a}}{1-e^2\cos^2\theta}\geq \frac{2b^2}{a}$,其中 $\theta$ 为直线倾斜角。
- 焦半径:设 $P(x,y)\in C,F_1(-c,0),F_2(c,0)$,则 $$|PF_1|=\sqrt{(x+c)^2+b^2\frac{a^2-x^2}{a^2}}=\sqrt{\frac{c^2}{a^2}x^2+2cx+a^2}=|a+ex|$$,同理 $|PF_2|=a-ex$,因此 $\red{\boxed{|PF|=|a\pm ex|}}$.
- 焦点弦( 过焦点的弦 ):设 $AB$ 是过 $\Gamma$ 的右焦点 $F$ 的一条弦,$A(x_1,y_1),B(x_2,y_2),\ AB$ 的倾斜角为 $\theta$,则 $$\red{\boxed{\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta},|AB|=\frac{2a(1-e^2)}{1-e^2\cos^2\theta}}}$$
证明:过 $A$ 作 $AA_1\perp AB$ 于点 $A_1$,则 $$|AF|=e|AA_1|=e\left(\frac{a^2}{c}-c-|AF|\cos\theta\right)\implies|AF|=\frac{b^2}{a+c\cos\theta}$$
同理 $\displaystyle|BF|=\frac{b^2}{a-c\cos\theta}$,代入得证。
注:一条过焦点的直线会有两个一长一短的焦半径,在公式中,**长的对应取减号,短的对应取加号;当焦点在 $y$ 轴上,将 $\cos\theta$ 换为 $\sin\theta$**.
- 过一个焦点 $F$ 作弦 $AB,AF=d_1,BF=d_2$,则 $\displaystyle\red{\boxed{\frac{1}{d_1}+\frac{1}{d_2}=\frac{2a}{b^2}}}$.( 难题中非常常用 )
- 中点弦问题:求直线 $AB$ 与圆锥曲线相交弦的中点 $M$ 和原点的连线 $OM$ 的斜率问题,有 $$\red{\boxed{k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}=e^2-1}}$$ 若焦点在 $y$ 轴,则 $\displaystyle k_{AB}\cdot k_{OM}=-\frac{a^2}{b^2}$.
证明:联立 $\Gamma$ 与 $y=k_{AB}x+m$ 得
$$(b^2+a^2k_{AB}^2)x^2+2mk_{AB}a^2x+a^2m^2-a^2b^2=0$$
所以 $\displaystyle x_1+x_2=\frac{-2mk_{AB}a^2}{b^2+a^2k_{AB}^2},M_x=\frac{x_1+x_2}{2}=\frac{-mk_{AB}a^2}{b^2+a^2k_{AB}^2},m=\frac{b^2+a^2k_{AB}^2}{-k_{AB}a^2}M_x$.
代入 $y=k_{AB}x+m$ 得 $\displaystyle y=-\frac{b^2}{k_{AB}a^2}x\implies k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}$.
例题:过椭圆 $\displaystyle\frac{x^2}{16}+\frac{y^2}{4}=1$ 内一点 $P(3,1)$,且被这点平分的弦所在的直线方程是 ?
方法一:( 点差法 )设 $$A(x_1,y_1),B(x_2,y_2)\implies \frac{x_1^2}{16}+\frac{y_1^2}{4}=1,\frac{x_2^2}{16}+\frac{y_2^2}{4}=1$$ 两式相减得 $$\frac{(x_1+x_2)(x_1-x_2)}{16}+\frac{(y_1+y_2)(y_1-y_2)}{4}=0$$
$P$ 为 $AB$ 中点 $\displaystyle \implies x_1+x_2=6,y_1+y_2=2 \implies k_{AB}=\frac{y_1-y_2}{x_1-x_2}=-\frac{3}{4}$.
所以直线 $AB$ 的方程是 $3x+4y-13=0$.
方法二:设弦为 $\displaystyle AB,k_{OP}=\frac{1}{3},k_{AB}=-\frac{b^2}{a^2}\div\frac{1}{3}=-\frac{3}{4}$,后同方法一。
- 中点弦问题的推广:椭圆上的点 $M$ 与过椭圆中心的弦 $AB$ 的端点的连线 $MA,MB$ 斜率之积为 $e^2-1$.
证明:作中位线 $OT$,易证 $\displaystyle k_{MA}\cdot k_{MB}=k_{MA}\cdot k_{OT}=-\frac{b^2}{a^2}=e^2-1$.
- 过 $\Gamma$ 上任意一点 $P$( 不是椭圆的顶点 )作椭圆的切线,设切线的斜率为 $k_1$,直线 $OP$ 的斜率为 $k_2$,则 $\boxed{k_1k_2=e^2-1}$,**双曲线同样成立**。
- 过原点 $O$ 的直线 $l$ 与椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 相交于 $A,B$ 两点,$P$ 为椭圆上任意一点,则 $k_{PA}k_{PB}=e^2-1$.
- 过 $\Gamma$ 上的任意一点 $P$( 非顶点 )作倾斜角互补的两条直线交椭圆于 $A,B$ 两点,有 $k_{AB}k_{OP}=1-e^2$.
**如果是焦点在 $y$ 轴上的椭圆或双曲线,则 $\boxed{e^2-1\to\frac{1}{e^2-1}}$**.
- $A,B$ 是 $\Gamma$ 上任意两点,$\displaystyle S_{\Delta AOB\max}=\frac{1}{2}ab$.
- $A,B$ 是 $\Gamma$ 上任意两点,并且 $\displaystyle OA\perp OB\implies \frac{1}{|OA|^2}+\frac{1}{|OB|^2}=\frac{1}{a^2}+\frac{1}{b^2}$.
- 椭圆两焦点到椭圆上任意一条切线的距离之积为定值 $b^2$.
证明:设切点为 $(x_0,y_0)$,切线方程为 $b^2x_0x+a^2y_0y=a^2b^2$,距离 $\displaystyle d_1=\frac{|-b^2x_0c-a^2b^2|}{\sqrt{b^4x_0^2+a^4y_0^2}},d_2=\frac{|b^2x_0c-a^2b^2|}{\sqrt{b^4x_0^2+a^4y_0^2}}$,则
$$d_1d_2=\frac{|a^4b^4-b^4x_0^2c^2|}{b^4x_0^2+a^4y_0^2}\xlongequal{b^2x_0^2+a^2y_0^2=a^2b^2}b^2\frac{a^4b^2-a^2b^2x_0^2+b^4x_0^2}{b^4x_0^2+a^4b^2-a^2b^2x_0^2}=b^2$$
#### 好题
1. 设直线 $l:y=x+1$ 与椭圆 $\displaystyle C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 相交于 $A,B$ 两点,与 $x$ 轴相交于左焦点 $F$,且 $\overrightarrow{AF}=3\overrightarrow{FB}$,则椭圆的离心率 $e=$ _______
答案:$\displaystyle\frac{\sqrt{2}}{2}$
解析:方法一:由题得 $F(-1,0),c=1$,设 $A(x_1,y_1),B(x_2,y_2)$,联立 $y=x+1$ 与椭圆方程 $b^2x^2+a^2y^2=a^2b^2$ 得
$(a^2+b^2)y^2-2b^2y+b^2-a^2b^2=0$,显然 $\displaystyle\Delta>0,y_1+y_2=\frac{2b^2}{a^2+b^2},y_1y_2=\frac{b^2-a^2b^2}{a^2+b^2}\ \circledast$
由 $\overrightarrow{AF}=3\overrightarrow{FB}$ 得 $0-y_1=3(y_2-0)$ 即 $y_1=-3y_2\ \circledcirc$
由 $\circledast \circledcirc$ 消去 $y_1,y_2$ 得 $-3b^2=(a^2+b^2)(1-a^2)\xRightarrow{a^2-b^2=c^2=1}a^4-3a^2+1=0\implies a=\pm\sqrt{2}\ 或\pm 1$.
取 $a=\sqrt{2}$,所以 $\displaystyle e=\frac{c}{a}=\frac{\sqrt{2}}{2}$.
方法二:注意上述关于焦点弦的结论,$\displaystyle\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta}=3$,代入 $\displaystyle\cos\theta=\frac{\sqrt{2}}{2}$ 可得 $\displaystyle e=\frac{\sqrt{2}}{2}$.
---
2. 已知椭圆 $\displaystyle\frac{x^2}{4}+y^2=1$,直线 $l:y=kx+m$ 满足 $m\neq -2k$ 且与椭圆相交于不同的两点 $A,B$,若以线段 $AB$ 为直径的圆始终过点 $Q(2,0)$,试判断直线 $l$ 是否过定点?若是,求出该定点的坐标;若不是,请说明理由。
解:设 $A(x_1,y_1),B(x_2,y_2)$,联立 $\begin{cases}
y=kx+m \\
\displaystyle\frac{x^2}{4}+y^2=1
\end{cases}$
得 $(1+4k^2)x^2+8kmx+4m^2-4=0,\Delta=16(4k^2-m+1)>0$
则 $\displaystyle x_1+x_2=\frac{-8km}{1+4k^2},x_1x_2=\frac{4m^2-4}{1+4k^2},y_1y_2=(kx_1+m)(kx_2+m)=\frac{m^2-4k^2}{1+4k^2}$.
因为以线段 $AB$ 为直径的圆过点 $Q$,所以 $\boxed{\overrightarrow{QB}\cdot\overrightarrow{QA}=0}$,又 $\overrightarrow{QB}=(x_2-2,y_2),\overrightarrow{QA}=(x_1-2,y_1)$.
所以 $\displaystyle\overrightarrow{QB}\cdot\overrightarrow{QA}=x_1x_2-2(x_1+x_2)+4+y_1y_2=\frac{(6k+5m)(2k+m)}{1+4k^2}=0$.
显然 $\displaystyle m=-\frac{6}{5}k\implies l:y=kx-\frac{6}{5}k=k\left(x-\frac{6}{5}\right)$,恒过定点 $\displaystyle\left(\frac{6}{5},0\right)$.
---
( **齐次化** )3. 已知 $\displaystyle\frac{x^2}{4}+\frac{y^2}{3}=1$,是否存在定圆与 $MN(OM\perp ON)$( 动直线 )总相切 ?
设 $MN:mx+ny=1$,代入得( 左边为 $2$ 次,右边为 $0$ 次,自然要在右边乘上 $2$ 次 )
$$3x^2+4y^2=12(mx+ny)^2\implies (3-12m^2)x^2+(4-12n^2)y^2-24mnxy=0$$
化成 $(4-12n^2)k^2-24mnk+3-12m^2=0$,因为 $\displaystyle k_1k_2=\frac{3-12m^2}{4-12n^2}=-1$,因此 $\displaystyle m^2+n^2=\frac{7}{12}$,定圆为 $\displaystyle x^2+y^2=\frac{12}{7}$.
---
( **定比点差法** )4. 已知 $\displaystyle\frac{x^2}{4}+y^2=1,A(-2,0)$,经过 $B(1,0)$ 且斜率存在的直线 $l$ 交椭圆于 $P,Q$ 两点,点 $C$ 与点 $P$ 关于坐标原点对称,连接 $AC,AQ$,求 $\displaystyle \frac{k_{AC}}{k_{AQ}}$ 的值。
设 $P(x_1,y_1),Q(x_2,y_2),\overrightarrow{PB}=\lambda\overrightarrow{BQ}$,则 $x_1+\lambda x_2=1+\lambda,y_1+\lambda y_2=0$.
$\begin{cases}\displaystyle \frac{x_1^2}{4}+y_1^2=1 \\ \displaystyle\frac{x_2^2}{4}+y_2^2=1 \end{cases}\implies \begin{cases} \displaystyle\frac{x_1^2}{4}+y_1^2=1 \\ \displaystyle\frac{\lambda^2 x_2^2}{4}+\lambda^2 y_2^2=\lambda^2 \end{cases}$
两式作差得 $\displaystyle\frac{(x_1+\lambda x_2)(x_1-\lambda x_2)}{4}+(y_1+\lambda y_2)(y_1-\lambda y_2)=1-\lambda ^2$.
代入解得 $\displaystyle x_1=\frac{5-3\lambda}{2},x_2=\frac{5\lambda -3}{2\lambda},\frac{k_{AC}}{k_{AQ}}=\frac{y_1(x_2+2)}{y_2(x_1-2)}=\frac{-\lambda(x_2+2)}{x_1-2}=\frac{3-9\lambda}{1-3\lambda}=3$.
- 练习题:设 $F_1,F_2$ 分别是椭圆 $\displaystyle\frac{x^2}{3}+y^2=1$ 的左右焦点,点 $A,B$ 在椭圆上,$\overrightarrow{F_1A}=5\overrightarrow{F_2B}$,则点 $A$ 的坐标是 ?答案:$(0,\pm 1)$.
---
( **正难则反** )5. 设椭圆 $\displaystyle\frac{x^2}{a^2}+y^2=1(a>1)$,若以点 $A(0,1)$ 为圆心的圆与椭圆至多有 $3$ 个公共点,求 $e$ 范围?
从反面考虑,若有 $4$ 个公共点,可知在 $y$ 轴两侧各有 $2$ 个交点,可知椭圆的一侧存在一个等腰 $\Delta APQ$ 满足 $AP=AQ$.
设 $PQ$ 中点为 $M(x_0,y_0)$,则 $\displaystyle k_{OM}k_{PQ}=e^2-1=-\frac{1}{a^2}$。因为 $\displaystyle k_{AM}k_{PQ}=\frac{y_0-1}{x_0}k_{PQ}=-1$,
所以两式相除得 $\displaystyle \frac{y_0-1}{y_0}=a^2>2$,得出 $\displaystyle e\in\left(0,\frac{\sqrt{2}}{2}\right]$.
---
( **齐次化 + 仿射变换** )6. ( 2022 I 卷 T22 )已知 $\displaystyle C:\frac{x^2}{6}+\frac{y^2}{3}=1,A(2,1)$,点 $M,N$ 在 $C$ 上,$AM\perp AN,AD\perp MN$,$D$ 为垂足,证明:存在定点 $Q$,使得 $|DQ|$ 是定值。
方法一:设 $MN:y=kx+m$,暴力联立 $+$ 向量得 $(2k+3m+1)(2k+m-1)=0$,得出 $MN$ 过定点 $\displaystyle P\left(\frac{2}{3},-\frac{1}{3}\right)$. 令 $\displaystyle Q\left(\frac{4}{3},\frac{1}{3}\right)$ 为 $AP$ 中点,得出 $\displaystyle|DQ|=\frac{1}{2}|AP|=\frac{2\sqrt{2}}{3}$ 是定值。
方法二:先将 $C$ 平移一下,变为 $\displaystyle\frac{(x+2)^2}{6}+\frac{(y+1)^2}{3}=1$,使得 $A$ 点在新坐标的原点上。设 $MN:mx+ny=1$,联立得 $\displaystyle(2+4n)\left(\frac{y}{x}\right)^2+4(m+n)\frac{y}{x}+4m+1=0$,显然 $\displaystyle\frac{y_1y_2}{x_1x_2}=\frac{4m+1}{2+4n}=-1$,得到 $\displaystyle \left(-\frac{4}{3}\right)m+\left(-\frac{4}{3}\right)n=1$,即定点 $\displaystyle\left(\frac{2}{3},-\frac{1}{3}\right)$.
---
7. $\displaystyle C:\frac{x^2}{6}+\frac{y^2}{3}=1,A(2,1)$,点 $M,N$ 在 $C$ 上,且 $AM\perp AN,AD\perp MN,D$ 为垂足,证明:① $MN$ 过定点 ②存在定点 $Q$ 使 $|DQ|$ 为定值。
①设 $MN:y=kx+m$,联立算 $\Delta$ 和 $\overrightarrow{AM}\cdot\overrightarrow{AN}$,得出 $m^2+9-3k^2>0$ 和 $(2k+m-\sqrt{3})(4k-m+2\sqrt{3})=0$,得 $m=4k+2\sqrt{3}$,定点 $P(-4,2\sqrt{3})$.
②由①得 $AP$ 中点 $\displaystyle Q\left(-1,\frac{3\sqrt{3}}{2}\right)$,因为 $AD\perp MN$,所以 $\displaystyle PQ=QA=QD=\frac{\sqrt{39}}{2}$.
---
( **点差法 + 二次代换消元** )8. ( 华南师大附中 2024 5 月测试 )已知 $\displaystyle E:\frac{x^2}{4}+y^2=1$,$E$ 上有 $3$ 点 $G,S,T$,直线 $ST$ 过点 $C(2,2)$,点 $M$ 为 $GS$ 中点且在直线 $y=x$ 上,证明:直线 $GT$ 与直线 $y=x$ 的交点为定点。
设 $S(x_1,y_1),T(x_2,y_2),G(x_3,y_3)$,进行一次点差法:$\displaystyle\frac{x_1^2}{4}+y_1^2=1,\frac{x_3^2}{4}+y_3^2=1$,相减得 $$\frac{y_1-y_3}{x_1-x_3}=-\frac{y_1+y_3}{4(x_1+x_3)}$$
因为 $GT$ 中点在 $y=x$ 上所以 $y_1+y_3=x_1+x_3$ 得 $\displaystyle y_1-y_3=-\frac{1}{4}(x_1-x_3)$.
两式相加得 $\displaystyle 2y_1=\frac{3}{4}x_1+\frac{5}{4}x_3\implies x_3=\frac{8y_1-3x_1}{5},y_3=\frac{3y_1+2x_1}{5}$
代入 $\displaystyle GT:\frac{y-y_3}{x-x_3}=\frac{y-y_2}{x-x_2}$ 得 $$(5y_2-3y_1-2x_1)x+(8y_1-3x_1-5x_2)y=-3(x_1y_2+x_2y_1)+8y_1y_2-2x_1x_2$$
设交点为 $(m,m)$,代入得 $5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)$
即证明存在 $m$ 使该式恒成立。
由直线 $ST$ 过点 $C(2,2),\displaystyle\frac{y_2-2}{x_2-2}=\frac{y_1-2}{x_1-2}\implies x_1(y_2-2)-x_2(y_1-2)=2(y_2-y_1)$,进行二次代换凑出和积:
$$x_1(y_2-2)+x_2(y_1-2)=\frac{x_1^2(y_2-2)^2-x_2^2(y_1-2)^2}{x_1(y_2-2)-x_2(y_1-2)}=\frac{(4-4y_1^2)(y_2-2)^2-(4-4y_2^2)(y_1-2)^2}{2(y_2-y_1)}=10(y_1+y_2)-8-8y_1y_2$$
即 $x_1y_2+x_2y_1=2(x_1+x_2)+10(y_1+y_2)-8-8y_1y_2$ ①
同理有 $(x_1-2)y_2-(x_2-2)y_1=-2(x_2-x_1)$
$$(x_1-2)y_2-(x_2-2)y_1=\frac{(x_1-2)^2y_2^2-(x_2-2)^2y_1^2}{(x_1-2)y_2-(x_2-2)y_1}=\frac{(x_1-2)^2(1-\frac{x_2^2}{4})-(x_2-2)^2(1-\frac{x_1^2}{4})}{-2(x_2-x_1)}$$
即 $\displaystyle x_1y_2+x_2y_1=(x_1+x_2)+2(y_1+y_2)-2-\frac{1}{2}x_1x_2$ ②
两式比对系数凑配出 $8y_1y_2-2x_1x_2$ 和目标式比对:
$4\times$ ② $-$ ① 得 $2(y_1+y_2)-2(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)$
对比 $5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)$ 得 $\displaystyle m=\frac{2}{5}$ 时恒成立。故定点为 $\displaystyle\left(\frac{2}{5},\frac{2}{5}\right)$.
<!-- ( **极点极线** )9. 已知 $A,B$ 分别为椭圆 $E:\frac{x^2}{9}+y^2=1$ 的左右顶点,$P$ 为直线 $x=6$ 上的动点,$PA$ 与 $E$ 的另一交点为 $C$,$PB$ 与 $E$ 的另一交点为 $D$,证明:$CD$ 过定点。
聪明的同学可以直接极点极线秒了,定点是 $(\frac{a^2}{6},0)$,但我们要求普通联立。
设 $P(6,t)$,联立椭圆方程得到 $\displaystyle C(\frac{27-3t^2}{t^2+9},\frac{6t}{t^2+9}),D(\frac{3t^2-3}{t^2+1},-\frac{2t}{t^2+1})$。
由对称性得定点在 $x$ 轴上,设其为 $T(s,0)$,于是 $k_{CT}=k_{TD}$,代入解得 $s=\frac{3}{2}$。计算量稍大。 -->
### 双曲线
- 概念:平面内到两个焦点 $F_1,F_2$ 的距离的差等于非零常数( 小于 $|F_1F_2|$ )的点的轨迹叫做双曲线。
双曲线就是下列点的集合 $P=\set{M|||MF_1|-|MF_2||=2a}$,$|F_1F_2|=2c>2a$.
| 标准方程 | $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\\$ 焦点在 $x$ 轴上 | $\displaystyle\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0)\\$ 焦点在 $y$ 轴上 |
|:-:|:-:|:-:|
| 顶点坐标 | $(\pm a,0)$ | $(0,\pm a)$ |
| 焦点坐标 | $(\pm c,0)$ | $(0,\pm c)$ |
| 渐近线方程 | $\displaystyle y=\pm\frac{b}{a}x$ | $\displaystyle y=\pm\frac{a}{b}x$ |
- $\boxed{c^2=a^2+b^2}$,离心率 $\boxed{e=\frac{c}{a}}\ (e>1)$
实轴长 $=2a$ 虚轴长 $=2b$. 等轴双曲线:$a=b$ 的双曲线。
$e$ 越大,双曲线开口越大。
一般方程:$Ax^2+By^2=1(AB<0)$.
双曲线与它的渐近线无限接近但永不相交,求渐近线方程时,只要令 $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=0$ 即可。
第二定义:平面内动点 $M$ 到定点 $F$ 的距离和它到准线 $\displaystyle l:x=\pm\frac{a^2}{c}$ 的距离之比等于 $e$.
- 与两定点 $A_1(-a,0),A_2(a,0)(a\neq 0)$ 连线的斜率之积为 $\displaystyle\frac{b^2}{a^2}=e^2-1$ 的点的轨迹为双曲线。
#### 双曲线焦点三角形的性质
双曲线 $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)$ 上异于顶点的点 $P(x_0,y_0)$ 与两焦点构成的 $\Delta PF_1F_2$ 叫做焦点三角形。以下记 $\angle F_1PF_2=\theta$。
1. 面积 $\red{\boxed{S=\frac{b^2}{\tan\frac{\theta}{2}}=c|y_0|}}$.
2. 设 $\angle PF_1F_2=\alpha,\angle PF_2F_1=\beta,P$ 为双曲线右支上一点,则 $$\frac{|PF_1|}{\sin\beta}=\frac{|PF_2|}{\sin\alpha}=\frac{|PF_1|-|PF_2|}{\sin\beta-\sin\alpha}=\frac{2a}{\sin\beta-\sin\alpha}=\frac{|F_1F_2|}{\sin(\alpha+\beta)}=\frac{2c}{\sin\theta}$$ 所以 $\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\beta-\sin\alpha}}$.
3. 若焦点三角形内切圆的圆心为 $I(x_1,y_1)$,与三边的切点分别为 $M,N,R$,则 $|F_1R|-|F_2R|=|F_1M|-|F_2N|=|PF_1|-|PF_2|=2a$,即 $c+x_1-(c-x_1)=2a$,解得 $\red{\boxed{x_1=a}}$.
4. 过双曲线焦点 $(c,0)$ 作渐近线 $\displaystyle y=\frac{b}{a}x$ 的垂线,垂足长度为 $b$,形成的三角形满足 $a^2+b^2=c^2$.
#### 双曲线的其它几何性质
以下记双曲线 $\displaystyle\Gamma:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)$.
- 通径:过 $\Gamma$ 的焦点作垂直于实轴所在的直线,该直线被双曲线截得的弦叫做通径,长度为 $\displaystyle\frac{2b^2}{a}$.
- 焦半径:双曲线一点 $P(x_0,y_0)$ 与左( 下 )焦点 $F_1$或右( 上 )焦点 $F_2$ 之间的线段叫做双曲线的焦半径,分别记作 $r_1=|PF_1|,r_2=|PF_2|$.
1. $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)$,若点 $P$ 在双曲线右支上,则 $r_1=ex_0+a,r_2=ex_0-a$;若点 $P$ 在双曲线左支上,则 $r_1=-ex_0-a,r_2=-ex_0+a$.
2. $\displaystyle\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\ (a>0,b>0)$,若点 $P$ 在双曲线上支上,则 $r_1=ey_0+a,r_2=ey_0-a$;若点 $P$ 在双曲线下支上,则 $r_1=-ey_0-a,r_2=-ey_0+a$.
总之,$\red{\boxed{r=\pm ex\pm a}}$.
- 设 $AB$ 是 $\Gamma$ 的一条弦,$AB$ 中点为 $M(x_0,y_0)$,则 $\displaystyle k_{AB}=\frac{b^2x_0}{a^2y_0}$,$\red{\boxed{k_{AB}k_{OM}=e^2-1}}$.
- 过 $\Gamma$ 的左焦点 $F(-c,0)$ 的直线交双曲线于 $A,B$ 两点,交 $y$ 轴于点 $P$,设 $\displaystyle\overrightarrow{PF}=\lambda_1\overrightarrow{FA}=\lambda_2\overrightarrow{FB}$,则 $\displaystyle\lambda_1+\lambda_2=\frac{2e^2}{1-e^2}$.
扩展:若 $F$ 改为 $x$ 轴上一点 $M(m,0)$,则 $\displaystyle\lambda_1+\lambda_2=\frac{2m^2}{a^2-m^2}$.
- 对于 $\Gamma$ 上一点 $P$ 做切线交两条渐近线于 $A,B$,则 $S_{\Delta PAB}=ab$.
#### 好题
1. 若双曲线的一条渐近线过点 $(8,-6)$,则其离心率等于 ?
分 $2$ 种情况讨论,焦点在 $x$ 轴上( $\displaystyle\frac{b}{a}=\frac{3}{4}\ \ \ e=\frac{5}{4}$ ),在 $y$ 轴上( $\displaystyle\frac{a}{b}=\frac{3}{4}\ \ \ e=\frac{5}{3}$ )
---
2. 动圆 $M$ 与圆 $C_1:(x+4)^2+y^2=1$,圆 $C_2:(x-4)^2+y^2=9$ 都外切,则动圆圆心 $M$ 的轨迹方程为 ?
解:圆 $C_1(-4,0),r_1=1,C_2(4,0),r_2=3$,设 $M(x,y)$,半径为 $r$,则 $\begin{cases}
|MC_1|=r+1 \\
|MC_2|=r+3
\end{cases}$
即 $|MC_2|-|MC_1|=2<|C_1C_2|$,所以 $M$ 的轨迹为以 $C_1,C_2$ 为焦点,$2a=2$ 的双曲线的**左支**,$b=\sqrt{15}$.
所以 $M$ 的轨迹方程为 $x^2-\frac{y^2}{15}=1\ (x\leq -1)$.
---
3. 是否存在过点 $\displaystyle P\left(1,-\frac{1}{2}\right)$ 的直线 $l$ 与双曲线 $\displaystyle\frac{x^2}{2}-y^2=1$ 相交于 $A,B$ 两点,且满足 $P$ 是线段 $AB$ 的中点?若存在,求出直线 $l$ 的方程;若不存在,请说明理由。
( **点差法** )解:设 $\displaystyle l:y=k(x-1)-\frac{1}{2},A(x_1,y_1),B(x_2,y_2)$,则 $\begin{cases}
\displaystyle\frac{x_1^2}{2}-y_1^2=1 \\
\displaystyle\frac{x_2^2}{2}-y_2^2=1
\end{cases}$,
两式相减得 $(x_1-x_2)(x_1+x_2)=2(y_1-y_2)(y_1+y_2)$,因为 $\displaystyle P\left(1,-\frac{1}{2}\right)$ 为线段 $AB$ 的中点,则
$$x_1+x_2=2,y_1+y_2=-1,k=\frac{y_1-y_2}{x_1-x_2}=\frac{x_1+x_2}{2(y_1+y_2)}=-1\implies l:y=-x+\frac{1}{2}$$
联立 $\begin{cases}
\displaystyle y=-x+\frac{1}{2} \\
\displaystyle\frac{x^2}{2}-y^2=1
\end{cases}$ 消去 $y$ 可得 $2x^2-4x+5=0,\Delta<0$,方程无实根,故 $l$ 不存在。
---
4. [ 安徽十校联盟 2023 期中 ] 已知双曲线 $\displaystyle C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)$ 的左、右焦点分别为 $F_1,F_2$,焦距为 $4$,点 $M$ 在圆 $E:x^2+y^2+4x-8y+16=0$ 上,且 $C$ 的一条渐近线上存在点 $N$,使得四边形 $OMNF_2$ 为平行四边形,$O$ 为坐标原点,则 $C$ 的离心率的取值范围为( )
$\text{A.} [2,+\infty)\ \ \ \ \ \ \text{B.} [\sqrt{3},+\infty)\ \ \ \ \ \ \text{C.} [4,+\infty)\ \ \ \ \ \ \text{D.} (1,\sqrt{3})$
答案:$\text{A}$.
<!-- 5. 已知直线 $y=ax+1$ 与双曲线 $3x^2-y^2=1$ 交于 $A,B$ 两点。
$(1)$ 若以 $AB$ 为直径的圆过坐标原点 $O$,求实数 $a$ 的值。
$(2)$ 是否存在这样的实数 $a$,使 $A,B$ 两点关于直线 $\displaystyle y=\frac{1}{2}x$ 对称?若存在,请求出 $a$ 的值;若不存在,请说明理由。
解:$(1)$ 联立 $\begin{cases}
y=ax+1\\
3x^2-y^2=1
\end{cases}$ 消去 $y$ 得 $(3-a^2)x^2-2ax-2=0$,依题意 $\begin{cases}
3-a^2\neq 0\\
\Delta >0
\end{cases}\\$
解得 $-\sqrt{6}< a<\sqrt{6}$ 且 $a\neq\pm\sqrt{3}$,设 $A(x_1,y_1),B(x_2,y_2)$,则 $\begin{cases}
\displaystyle x_1+x_2=\frac{2a}{3-a^2} \\
\displaystyle x_1x_2=\frac{-2}{3-a^2}
\end{cases}$
由题,$\therefore OA\perp OB,\ \overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=0\ \ \ \ \ \ \because y_1y_2=a^2x_1x_2+a(x_1+x_2)+1$
$\therefore x_1x_2+y_1y_2=(a^2+1)x_1x_2+a(x_1+x_2)+1=(a^2+1)\cdot\frac{-2}{3-a^2}+\frac{2a^2}{3-a^2}+1=0\implies a=\pm 1$
$(2)$ 假设存在实数 $a$,使 $A,B$ 两点关于直线 $\displaystyle y=\frac{1}{2}x$ 对称,则 $a=-2$ 检验后可排除,故 $a$ 不存在。 -->
### 抛物线
- 概念:平面内与一个定点 $F$ 和一条定直线 $l$( 不经过点 $F$ )的距离相等的点的轨迹叫做抛物线。
| 标准方程 | $y^2=2px\ (p>0)$ | $y^2=-2px\ (p>0)$ | $x^2=2py\ (p>0)$ | $x^2=-2py\ (p>0)$ |
|:-:|:-:|:-:|:-:|:-:|
| 开口方向 | 向右 | 向左 | 向上 | 向下 |
| 焦点坐标 | $\displaystyle\left(\frac{p}{2},0\right)$ | $\displaystyle\left(-\frac{p}{2},0\right)$ | $\displaystyle\left(0,\frac{p}{2}\right)$ | $\displaystyle\left(0,-\frac{p}{2}\right)$ |
| 准线 | $\displaystyle x=-\frac{p}{2}$ | $\displaystyle x=\frac{p}{2}$ | $\displaystyle y=-\frac{p}{2}$ | $\displaystyle y=\frac{p}{2}$ |
抛物线的离心率 $e=1$.
通径:过抛物线的焦点作垂直于对称轴的直线,交抛物线于 $AB$,线段 $AB$ 就是抛物线的通径,长为 $2p$,是所有过焦点的弦中最短的。
#### 抛物线焦点弦的性质
$AB$ 为过抛物线 $y^2=2px\ (p>0)$ 的焦点 $\displaystyle F\left(\frac{p}{2},0\right)$ 的弦,点 $A(x_1,y_1),B(x_2,y_2)$ 在准线上的射影分别为点 $\displaystyle A_1\left(-\frac{p}{2},y_1\right),B_1\left(-\frac{p}{2},y_2\right)$.
1. $\displaystyle |AF|=|AA_1|=x_1+\frac{p}{2},|BF|=|BB_1|=x_2+\frac{p}{2},|AB|=x_1+x_2+p$.
2. $\displaystyle x_1x_2=\frac{p^2}{4},y_1y_2=-p^2$.
证明:当直线 $AB$ 的斜率存在时,设 $\displaystyle AB:y=k\left(x-\frac{p}{2}\right),k\neq 0$,联立抛物线方程和直线方程得 $\displaystyle y^2-\frac{2p}{k}y-p^2=0$.
易知 $\Delta>0$,所以 $\displaystyle y_1y_2=-p^2,x_1x_2=\frac{y_1^2}{2p}\frac{y_2^2}{2p}=\frac{p^2}{4}$,同理可证直线 $AB$ 的斜率不存在时,命题也成立。
3. 以 $|AB|$ 为直径的圆与抛物线的准线相切。
证明:设 $AB$ 中点为 $D$,$D$ 到准线的距离为 $d$,则 $\displaystyle d=\frac{|AA_1|+|BB_1|}{2}=\frac{|AB|}{2}$,原命题得证。
4. 以 $|AF|$ 为直径的圆与 $y$ 轴相切。
5. $\displaystyle \frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p}$
证明:当直线 $AB$ 的斜率存在时,$$\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{1}{|AA_1|}+\frac{1}{|BB_1|}=\frac{1}{x+\frac{p}{2}}+\frac{1}{x_2+\frac{p}{2}}\\=\frac{x_1+x_2+p}{x_1x_2+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{x_1+x_2+p}{\frac{p^2}{4}+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{2}{p}$$
同理可证直线 $AB$ 的斜率不存在时,命题也成立。
6. 若直线 $AB$ 的倾斜角为 $\alpha$,则 $\displaystyle|AB|=\frac{2p}{\sin^2\alpha}$
证明:当直线 $AB$ 的斜率存在时,设 $\displaystyle AB:y=k\left(x-\frac{p}{2}\right),k\neq 0$,由 $\begin{cases}\displaystyle y=k\left(x-\frac{p}{2}\right) \\ y^2=2px\end{cases}$ 得 $ky^2-2py-kp^2=0$. 易知 $\displaystyle\Delta>0,y_1+y_2=\frac{2p}{k},y_1y_2=-p^2$
$$|AB|=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}=\sqrt{1+\frac{1}{k^2}}\cdot\frac{2p\sqrt{1+k^2}}{|k|}=\frac{2p(1+k^2)}{k^2}=\frac{2p(1+\tan^2\alpha)}{\tan^2\alpha}=\frac{2p}{\sin^2\alpha}$$
当直线 $AB$ 的斜率不存在时,$\displaystyle|AB|=2p=\frac{2p}{\sin^2 90\degree}$,命题也成立。
推广:$\red{\boxed{|AF|=\frac{p}{1-\cos\alpha},|BF|=\frac{p}{1+\cos\alpha}}}$,$O$ 到 $AB$ 的距离 $\displaystyle =\frac{p\sin\alpha}{2},S_{\Delta AOB}=\frac{p^2}{2\sin\theta}$.
注:若抛物线为 $x^2=\pm 2py$,将上述 $\cos$ 换为 $\sin$,$\sin$ 换为 $\cos$.
7. $A,O,B_1$ 三点共线,$A_1,O,B$ 三点共线。
设 $\displaystyle AB:x=my+\frac{p}{2}$ 即可通过斜率相等证明。
8. $A_1F\perp B_1F$.
9. 对于 $y^2=2px(p>0)$,当直线过点 $(a,0)$ 与抛物线交于 $P,Q$,则 $\displaystyle k_{OP}k_{OQ}=-\frac{2p}{a}$.
10. 对于 $y^2=2px$,$AB$ 为其一条弦,则 $\displaystyle k_{AB}=\frac{2p}{y_1+y_2}$;对于 $x^2=2py$,则 $\displaystyle k_{AB}=\frac{x_1+x_2}{2p}$.
#### 好题
1. 过点 $Q(4,1)$ 作抛物线 $y^2=8x$ 的弦 $AB$,恰被点 $Q$ 平分,则弦 $AB$ 所在直线的方程为 ?
( **点差法** )解:设 $A(x_1,y_1),B(x_2,y_2)$,则 $\begin{cases} y_1^2=8x_1 (1) \\ y_2^2=8x_2 (2)\end{cases}$,因为 $Q(4,1)$ 是 $AB$ 中点,所以 $\begin{cases} x_1+x_2=8 \\ y_1+y_2=2 \end{cases}(3)$
$(1)-(2)$ 得 $(y_1+y_2)(y_1-y_2)=8(x_1-x_2)\ \ \ \text{}$ 把 $(3)$ 代入得 $\displaystyle\frac{y_1-y_2}{x_1-x_2}=4$,所以 $AB:y=4x-15$.
---
2. 已知抛物线 $C:y^2=4x$ 的焦点为 $F$,直线 $l$ 过焦点 $F$ 与 $C$ 交于 $A,B$ 两点,以 $AB$ 为直径的圆与 $y$ 轴交于 $D,E$ 两点,且 $\displaystyle|DE|=\frac{4}{5}|AB|$,则直线 $l$ 的方程为_____
解:设 $|AB|=2r(2r\geq 4)$,$AB$ 的中点为 $M$,作 $MN\perp y$ 轴于点 $N$,过 $A,B$ 分别作准线 $l:x=-1$ 的垂线,垂足为 $A_1,B_1$.
显然 $2(|MN|+1)=|AA_1|+|BB_1|=|AF|+|BF|=|AB|=2r$,所以 $\displaystyle|MN|=r-1,|DE|=2\sqrt{r^2-(r-1)^2}=\frac{8}{5}r$.
解得 $\displaystyle r=\frac{5}{2}\ 或\ \frac{5}{8}$( 舍 ),所以 $\displaystyle M_x=\frac{3}{2}$,设直线 $l:y=k(x-1),A(x_1,y_1),B(x_2,y_2)$.
联立 $\begin{cases} y=k(x-1) \\ y^2=4x\end{cases}$ 得 $k^2x^2-(2k^2+4)x+k^2=0\implies\displaystyle x_1+x_2=\frac{2k^2+4}{k^2}=3$,解得 $k=\pm 2$.
故直线 $l$ 的方程为 $2x\pm y-2=0$.
---
3. ( 多选 )已知点 $F$ 是抛物线 $y^2=2px\ (p>0)$ 的焦点,$AB,CD$ 是经过点 $F$ 的弦,且 $AB\perp CD$,直线 $AB$ 的斜率为 $k$ 且 $k>0$,$A,C$ 两点在 $x$ 轴上方,以下一定成立的有( )
$\displaystyle\text{A.}\ \frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{B.}$ 若 $\displaystyle|AF|\cdot|BF|=\frac{4}{3}p^2$,则 $\displaystyle k=\frac{\sqrt{3}}{3}$
$\text{C.}\ \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OD}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{D.}$ 四边形 $ACBD$ 面积的最小值为 $16p^2$
答案:$\text{AC}$
解析:$\text{A.}$ 由题得 $\displaystyle k_{CD}=-\frac{1}{k}$,设 $\displaystyle AB:y=k\left(x-\frac{p}{2}\right)$,联立 $\begin{cases} \displaystyle y=k\left(x-\frac{p}{2}\right) \\ y^2=2px\end{cases}$ 得
$$k^2x^2-p(k^2+2)x+\frac{1}{4}k^2p^2=0\implies x_1+x_2=\frac{p(k^2+2)}{k^2},x_1x_2=\frac{1}{4}p^2\\\implies |AB|=x_1+x_2+p=\frac{2p(k^2+1)}{k^2}$$
同理 $|CD|=2p(1+k^2)$,则有 $\displaystyle\frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}$.
$\displaystyle\text{B.}\ |AF|\cdot|BF|=\left(x_1+\frac{p}{2}\right)\left(x_2+\frac{p}{2}\right)=p^2+\frac{p^2}{k^2}=\frac{4}{3}p^2\implies k=\sqrt{3}$
$\displaystyle\text{C.}\ \overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=\frac{1}{4}p^2+k^2\left(x_1-\frac{p}{2}\right)\left(x_2-\frac{p}{2}\right)=-\frac{3}{4}p^2$,与 $k$ 无关,同理 $\displaystyle\overrightarrow{OC}\cdot\overrightarrow{OD}=-\frac{3}{4}p^2$
$\text{D.}$ 因为 $AB\perp CD$ 所以 $\displaystyle S=\frac{1}{2}|AB|\cdot|CD|=\frac{1}{2}\frac{2p(k^2+1)}{k^2}\cdot 2p(1+k^2)=2p^2\left(k^2+\frac{1}{k^2}+2\right)\geq 8p^2$ 当且仅当 $k=1$ 取等。
---
( **同构** )4. ( $2011$ 浙江卷 )已知抛物线 $C_1:x^2=y$,圆 $C_2:x^2+(y-4)^2=1$ 的圆心为点 $M$. 已知 $P$ 是抛物线 $C_1$ 上的点( 异于原点 ),过点 $P$ 作圆 $C_2$ 的两条切线,分别交 $C_1$ 于点 $A,B$,若过点 $M,P$ 两点的直线 $l$ 垂直于 $AB$,求直线 $l$ 的方程。
设 $P(x_0,x_0^2),A(x_1,x_1^2),B(x_2,x_2^2)$,则 $k_{AB}=x_1+x_2$,$PA:y-x_0^2=(x_1+x_0)(x-x_0)$,即 $(x_1+x_0)x-y-x_1x_0=0$.
从而 $\displaystyle 1=\frac{|4+x_1x_0|}{\sqrt{(x_1+x_0)^2+1}}$,整理得 $(1-x_0^2)x_1^2-6x_1x_0+x_0^2-15=0$,同理 $(1-x_0^2)x_2^2-6x_2x_0+x_0^2-15=0$.
显然 $x_1,x_2$ 是方程 $(1-x_0^2)x^2-6xx_0+x_0^2-15=0$ 的两根,$\displaystyle x_1+x_2=\frac{6x_0}{1-x_0^2}=k_{AB}$,因为 $\displaystyle k_l=\frac{x_0^2-4}{x_0}$.
所以可以解得 $\displaystyle x_0^2=\frac{23}{5},l:y=\pm\frac{3\sqrt{115}}{115}x+4$.
---
( **向量** )5. 已知抛物线 $\displaystyle y=x^2,A\left(-\frac{1}{2},\frac{1}{4}\right),B\left(\frac{3}{2},\frac{9}{4}\right)$,抛物线上的 $\displaystyle P(x,y)\left(-\frac{1}{2}<x<\frac{3}{2}\right)$,过点 $B$ 作直线 $AP$ 的垂线,垂足为 $Q$,求 $|PA|\cdot|PQ|$ 的最大值。
设 $AB$ 中点为 $\displaystyle M\left(\frac{1}{2},\frac{5}{4}\right)$,从而
$$\begin{aligned}|PA|\cdot|PQ|&=-\overrightarrow{PA}\cdot\overrightarrow{PQ}=-\overrightarrow{PA}\cdot(\overrightarrow{PB}+\overrightarrow{BQ})=-\overrightarrow{PA}\cdot\overrightarrow{PB}=\left(\frac{\overrightarrow{PA}-\overrightarrow{PB}}{2}\right)^2-\left(\frac{\overrightarrow{PA}+\overrightarrow{PB}}{2}\right)^2\\&=2-|PM|^2=\left(x+\frac{1}{2}\right)^3\left(\frac{3}{2}-x\right)=\frac{1}{3}\left(x+\frac{1}{2}\right)\left(x+\frac{1}{2}\right)\left(x+\frac{1}{2}\right)\left(\frac{9}{2}-3x\right)\\&\leq \frac{1}{3}\left[\displaystyle\frac{\left(x+\frac{1}{2}\right)+\left(x+\frac{1}{2}\right)+\left(x+\frac{1}{2}\right)+\left(\frac{9}{2}-3x\right)}{4}\right]^4\leq\frac{27}{16}\end{aligned}$$
当且仅当 $x=1$ 时取等号。
---
( **齐次化** )6. 抛物线 $C:y^2=2px$,设 $A,B$ 为抛物线上的点,$OA\perp OB$,证明 $AB$ 过定点。
设 $AB:mx+ny=1$,联立 $y^2=2px(mx+ny)\implies y^2-2pnxy-2pmx^2=0$,同时除以 $x^2$ 得:
$\displaystyle \left(\frac{y}{x}\right)^2-2pn\frac{y}{x}-2pm=0\implies\frac{y_1}{x_1}\frac{y_2}{x_2}=-2pm=-1$,得 $2pm=1$,因此定点为 $(2p,0)$.
---
( **同构** )7. $C:x^2=4y$,直线 $l$ 与 $C$ 交于 $P,Q$ 两点,点 $M$ 在 $y=-\sqrt{1-x^2}$ 上,$MP,MQ$ 中点均在 $C$ 上,求 $S_{\Delta MPQ}$ 范围。
设 $P(x_1,y_1),Q(x_2,y_2),M(x_0,y_0)$,$PM$ 中点 $\displaystyle\left(\frac{x_1+x_0}{2},\frac{y_1+y_0}{2}\right)$ 与 $C$ 联立得
$$(x_1+x_0)^2=8(y_1+y_0)\implies x_1^2+2x_1x_0+x_0^2=2x_1^2+8y_0\implies x_1^2-2x_0x_1+(8y_0-x_0^2)=0$$
将 $x_1$ 换成 $x_2$ 得到类似的式子,于是 $x_1,x_2$ 是方程 $x^2-2x_0x+(8y_0-x_0^2)=0$ 的两个根,得到 $x_1+x_2=2x_0$.
还可得到 $\displaystyle\Delta=8(x_0^2-4y_0),\frac{y_1+y_2}{2}=\frac{6x_0^2-16x_0}{8}$,于是
$$S_{\Delta MPQ}=\frac{1}{2}\frac{6x_0^2-24x_0}{8}\sqrt{8(x_0^2-4y_0)}=\frac{3\sqrt{2}}{4}(x_0^2-4y_0)^{\frac{3}{2}}$$
因为 $y_0\in[-1,0]$,所以 $\displaystyle S\in\left[-\frac{3\sqrt{2}}{4},6\sqrt{2}\right]$.
### 其他问题
#### 共焦点问题
已知 $F_1,F_2$ 为椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$( 离心率 $e_1$ )和双曲线 $\displaystyle\frac{x^2}{m^2}-\frac{y^2}{n^2}=1(a>b>0)$( 离心率 $e_2$ )的公共焦点,$P(x_0,y_0)$ 是一个公共点,$\angle F_1PF_2=\theta$,则
$$|x_0|=\frac{am}{c}\ \ \ \ \ |y_0|=\frac{bn}{c}$$
$$|PF_1|\cdot|PF_2|=a^2-m^2\ \ \ \ \ \ \overrightarrow{PF_1}\cdot\overrightarrow{PF_2}=b^2-n^2\ \ \ \ \ \ S_{\Delta PF_1F_2}=bn$$
$$\tan\frac{\theta}{2}=\frac{n}{b}\ \ \ \ \ \ \cos\theta=\frac{b^2-n^2}{a^2-m^2}$$
$$\left(\frac{n}{e_1}\right)^2+\left(\frac{b}{e_2}\right)^2=b^2+n^2$$
$$\boxed{\frac{\sin^2\frac{\theta}{2}}{e_1^2}+\frac{\cos^2\frac{\theta}{2}}{e_2^2}=1}\implies \boxed{\frac{1-\cos\theta}{e_1^2}+\frac{1+\cos\theta}{e_2^2}=2}$$
因此可以推出 $\displaystyle e_1e_2\geq 2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=\sin\theta$.
#### 一类求离心率的问题
对于焦点 $F$ 在 $x$ 轴上的圆锥曲线 $C$,经过 $F$ 的直线交 $C$ 于 $A,B$ 两点,倾斜角为 $\theta$,斜率为 $k$,$\overrightarrow{AF}=\lambda\overrightarrow{FB}$,则
$$|e\cos\theta|=\left|\frac{\lambda-1}{\lambda+1}\right|\ \ \ \ \ \ e=\sqrt{k^2+1}\left|\frac{\lambda-1}{\lambda+1}\right|$$
若是双曲线,则变为 $\displaystyle\left|\frac{\lambda+1}{\lambda-1}\right|$;若是焦点在 $y$ 轴上,则变为 $\sin\theta$ 和 $\displaystyle\sqrt{1+\frac{1}{k^2}}$.
#### 一类求轨迹方程的问题——交轨法
例题:坐标系中 $P(-2,2),Q(0,2)$,直线 $l:y=x$,长度为 $\sqrt{2}$ 的线段 $AB$ 在 $l$ 上运动,延长 $PA,QB$ 交于点 $M$,求 $M$ 轨迹方程。
设 $A(a,a),B(a+1,a+1)$,那么 $\displaystyle PA:y-2=\frac{a-2}{a+2}(x+2),PB:y-2=\frac{a-1}{a+1}x$,稍加转换变为
$$PA:\frac{y-2}{x+2}=\frac{a-2}{a+2}\implies\frac{x+y}{x-y+4}=\frac{2a}{4}=\frac{a}{2}$$
$$PB:\frac{y-2}{x}=\frac{a-1}{a+1}\implies\frac{x+y-2}{x-y+2}=\frac{2a}{2}=a$$
因此 $\displaystyle 2\frac{x+y}{x-y+4}=\frac{x+y-2}{x-y+2}$,即 $\displaystyle \frac{(y+1)^2}{8}-\frac{(x+1)^2}{8}=1$.
注意上述运算是在 $a\neq -2,-1$ 时进行的,需要单独验证 $a=-2,-1$.
#### 伯努利双纽线
定义:平面中一点 $P$ 到点 $F_1(-a,0),F_2(a,0)$ 的距离的乘积是定值 $a^2$ 的曲线。即
$$|PF_1|\cdot|PF_2|=\sqrt{(x-a)^2+y^2}\sqrt{(x+a)^2+y^2}=a^2$$
可以化简为
$$(x^2+y^2)^2=2a^2(x^2-y^2)$$
一些性质:
1. 关于原点中心对称。
2. $\displaystyle \red{\boxed{x_p\in[-\sqrt{2}a,\sqrt{2}a],y_p\in\left[-\frac{a}{2},\frac{a}{2}\right]}}$
3. 每个弧形的面积是 $a^2$.( From Baidu )
#### 极点极线问题
设圆锥曲线 $C:Ax^2+By^2+Cxy+Dx+Ey+F=0$,平面上任意一点 $P(x_0,y_0)$,则极点 $P$ 关于 $C$ 的极线方程是
$$\red{\boxed{Ax_0x+By_0y+C\frac{x_0y+y_0x}{2}+D\frac{x_0+x}{2}+E\frac{y_0+y}{2}+F=0}}$$
也就是说:
1. $x^2,y^2$ 换成 $x_0x,y_0y$.
2. $xy$ 换成 $\displaystyle\frac{x_0y+y_0x}{2}$.
3. $x,y$ 换成 $\displaystyle\frac{x_0+x}{2},\frac{y_0+y}{2}$.
4. 常数项不变。
例如对于椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$P$ 的极线方程为 $\displaystyle\boxed{\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1}$;当 $P$ 是焦点时,极线 $=$ 准线,即 $\displaystyle x=\frac{a^2}{c}$.
极点 $P$ 和极线 $l$ 的【位置关系】满足:
1. $P$ 在圆锥曲线外,则 $l$ 为 $P$ 点处的切点弦方程( 过 $P$ 作两条切线,切点的连线 )。
2. $P$ 在圆锥曲线上,则 $l$ 为 $P$ 点处的切线方程。
3. $P$ 在圆锥曲线内,则 $l$ 为与圆锥曲线相离的一条直线( 虚切点弦方程,过 $P$ 作弦,再做交点的两条切线,切线的交点的轨迹方程 )。
【部分证明】
设 $CD:x=ty+m,C(x_1,y_1),D(x_2,y_2),N(m,0)$,则 $\displaystyle y_1+y_2=\frac{-2b^2mt}{a^2+b^2t^2},y_1y_2=\frac{b^2m^2-a^2b^2}{a^2+b^2t^2}$
注意到 $\displaystyle m(y_1+y_2)+2ty_1y_2=\frac{-2a^2b^2t}{a^2+b^2t^2}=\frac{a^2}{m}(y_1+y_2)$
有 $\displaystyle AC:x=\frac{x_1+a}{y_1}y-a,BD:x=\frac{x_2-a}{y_2}y+a$,联立得
$$\frac{ty_1+m+a}{y_1}y-a=\frac{ty_2+m-a}{y_2}y+a\implies\frac{m+a}{y_1}y-\frac{m-a}{y_2}y=2a$$
$$\begin{aligned}y_M&=\frac{2ay_1y_2}{m(y_2-y_1)+a(y_1+y_2)}\\x_M&=\frac{a^2(y_2-y_1)+2aty_1y_2+am(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}\\&=\frac{a^2(y_2-y_1)+a\cdot\frac{a^2}{m}(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}=\frac{a^2}{m}\end{aligned}$$
【性质】
过 $P$ 作直线 $PQ$,交极线 $MN$ 于 $Q$,交椭圆于 $A,B$ 两点 $\displaystyle\iff\frac{|PA|}{|PB|}=\frac{|QA|}{|QB|}$( 调和点列 )
<!-- #### 与定值 $\frac{2}{e}$ 有关的问题:
1. 若 $AB$ 是过椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的焦点 $F$ 的焦点弦,$AB$ 的垂直平分线交 $x$ 轴于点 $M$,则 $\frac{|AB|}{|FM|}$ 为定值 $\frac{2}{e}$。
证明:设 $F$ 为左焦点,以 $F$ 为极点,$x$ 轴为极轴建立极坐标系,得极坐标方程 $\rho = \frac{ep}{1-e\cos\theta}$,
所以 $|AB|=\rho_1+\rho_2=\frac{2ep}{1-e^2\cos^2\theta}$,$|FM|=\frac{1}{|\cos\theta|}|\frac{\rho_1-\rho_2}{2}|=\frac{e^2p}{1-e^2\cos^2\theta}\implies\frac{|AB|}{|FM|}=\frac{2}{e}$
2. 椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左焦点为 $F$,在 $x$ 轴上点 $F$ 右侧有一点 $A$,以 $FA$ 为直径作半径为 $R$ 的圆,在 $x$ 轴上方部分交于 $N,M$ 两点,则 $\frac{|FM|+|FN|}{R}=\frac{2}{e}$
证明:设圆为 $[x-(R-c)]^2+y^2=R^2$,联立得 $x_1+x_2=\frac{2a^2(R-c)}{c^2},|FM|+|FN|=a+ex_1+a+ex_2=\frac{2R}{e}$
3. 若 $AB$ 为椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 焦点 $F$ 的弦,$FM$ 为与焦点 $F$ 对应的焦准距,则 $\frac{|AB||FM|}{|FA||FB|}=\frac{2}{e}$
证明:同 1 建极坐标系,$|FM|=p,|FA|=\frac{ep}{1-e\cos\theta},|FB|=\frac{ep}{1+e\cos\theta},|AB|=|FA|+|FB|=\frac{2ep}{1-e^2\cos^2\theta},|FA||FB|=\frac{e^2p^2}{1-e^2\cos^2\theta}$。
4. 已知椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左右焦点分别为 $F_1,F_2,A(-a,0),B(a,0)$,点 $P$ 是椭圆上的点( 不与 $A,B$ 重合 ),$\angle APB=2\alpha,\angle F_1PF_2=2\beta,|\tan\beta\tan 2\alpha|$ 为定值 $\frac{2}{e}$ -->
#### 光学性质
【椭圆】:设 $F_1,F_2$ 是椭圆的两个焦点,从 $F_1$ 出发的光线经过反射必经过 $F_2$.
【双曲线】:设 $F_1,F_2$ 是双曲线的两个焦点,从 $F_1$ 出发的光线经过反射后的**反向延长线**必经过 $F_2$.
【抛物线】:设 $F$ 为焦点,从 $F$ 出发的光线经过反射后,平行于对称轴。
【椭圆+抛物线】设 $P$ 为反射点,$AB$ 为 $P$ 处的切线,$PT$ 平分 $\angle F_1PF_2$,则 $PT\perp AB$.
【2025 八省联考 T18】已知椭圆 $\displaystyle C:\frac{x^2}{4}+\frac{y^2}{3}=1$,左右焦点 $F_1(-1,0),F_2(1,0)$,设 $M$ 是坐标平面上的动点,且线段 $F_1M$ 的垂直平分线与 $C$ 恰有一个公共点,证明 $M$ 的轨迹为圆,并求该圆的方程。
设 $A$ 点为切点,由光学性质,从左焦点 $F_1$ 出发经过 $A$ 点,且被椭圆反射的光线会经过 $F_2$.
显然 $|AF_1|=|AM|$,故 $|MF_2|=|MA|+|AF_2|=|AF_1|+|AF_2|=2a=4$,所以 $M:(x-1)^2+y^2=16$.
#### 仿射变换
设 $a>0,b>0$,将原来曲线上的每个点的横坐标乘以 $a$,纵坐标乘以 $b$,形成了新的曲线。
【性质】:
1. 对原来的两条曲线作仿射变换,交点数不变。
2. 对曲线 $f(x,y)=0$ 作仿射变换,曲线变为 $\displaystyle f\left(\frac{x}{a},\frac{y}{b}\right)=0$.
3. 对面积为 $S$ 的曲线作仿射变换,面积变为 $abS$.
4. 对直线 $Ax+By+C=0$ 作仿射变换,变为 $\displaystyle\frac{A}{a}x+\frac{B}{b}y+C=0$.
#### $\text{Monge}$ 蒙日圆
过圆锥曲线外一点作两条互相垂直的切线,那么这一点的轨迹是一个圆,这个圆被称为蒙日圆,又叫外准圆。注意双曲线要满足 $e\in(1,\sqrt{2})$.
| 椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ | 双曲线 $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(\red{a>b}>0)$ | 抛物线 $y^2=2px(p>0)$ |
|:-:|:-:|:-:|
| $\red{\boxed{x^2+y^2=a^2+b^2}}$ | $x^2+y^2=a^2-b^2$ | $\displaystyle x=-\frac{p}{2}$ |
#### $\text{Candy}$ 坎迪定理
设 $M$ 是已知圆锥曲线中定弦 $PQ$ 上一点,过点 $M$ 作两条任意弦 $AB$ 和 $CD$,若 $AD$ 和 $BC$ 分别交 $PQ$ 于 $T$ 和 $S$,则
$$\displaystyle\frac{1}{MT}-\frac{1}{MQ}=\frac{1}{MS}-\frac{1}{MP}$$
<img src="https://cdn.luogu.com.cn/upload/image_hosting/vsax355a.png" width="300" height="200">
直接推论:蝴蝶定理:令 $MP=MQ$ 即可得到 $MS=MT$.
#### $\text{Archimedes}$ 阿基米德三角形
圆锥曲线的弦和过弦端点的两条切线所围成的三角形称为阿基米德三角形,该弦称为底边。
【2006 高考】已知抛物线 $x^2=4y$ 的焦点为 $F$,点 $A,B$ 是抛物线上两个动点,且 $\overrightarrow{AF}=\lambda\overrightarrow{FB}(\lambda>0)$,过 $A,B$ 两点分别作抛物线的切线,设其交点为 $M$,证明:$\overrightarrow{FM}\cdot\overrightarrow{AB}$ 是定值。
解:设 $\displaystyle A\left(x_1,\frac{x_1^2}{4}\right),B\left(x_2,\frac{x_2^2}{4}\right)$,由 $\overrightarrow{AF}=\lambda\overrightarrow{FB}$ 得 $x_1x_2=-4$.
已知抛物线方程为 $y=\frac{1}{4}x^2$,求导得 $y'=\frac{1}{2}x$,所以过 $A,B$ 两点的切线方程是 $$y=\frac{1}{2}x_1x-\frac{1}{4}x_1^2,y=\frac{1}{2}x_2x-\frac{1}{4}x_2^2$$
交点 $\displaystyle M\left(\frac{x_1+x_2}{2},-1\right)$,所以 $\displaystyle\overrightarrow{FM}=\left(\frac{x_1+x_2}{2},-2\right),\overrightarrow{AB}=\left(x_2-x_1,\frac{x_2^2-x_1^2}{4}\right)$,从而 $\overrightarrow{FM}\cdot\overrightarrow{AB}=0$.
扩展开来,对于抛物线 $y^2=2px(p>0)$ 的焦点 $F$ 的直线交抛物线于 $A,B$ 两点,过 $A,B$ 两点的切线交于 $M$,则 $\boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0}$,并且 **$M$ 在准线上**,并且 $\boxed{|MF|^2=|FA|\cdot|FB|}$.( 证明 $MA\perp MB$ 即可,射影定理 )
对于椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左焦点 $F$ 任意做一条直线 $AB$,交椭圆于 $A,B$ 两点,分别过 $A,B$ 作椭圆的切线交于点 $M$,则 **$M$ 在左准线上**,且 $\boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0}$.( 通过设 $A(a\cos\theta_1,b\sin\theta_1)$ 等证明 )
阿基米德三角形面积公式为
$$S=\frac{1}{p}(x_p^2-2py_p)^{\frac{3}{2} }$$
#### $\text{Cauchy}$ 柯西不等式的应用
1. 设椭圆 $\displaystyle C:\frac{x^2}{16}+\frac{y^2}{12}=1,M(2,\sqrt{2})$,过点 $P(-8,0)$ 的直线与 $C$ 交于 $A,B$ 两点,求 $\Delta ABF$ 面积的最大值。
设 $A(x_1,y_1),B(x_2,y_2)$,由 $P,A,B$ 三点共线得 $\displaystyle k_{PA}=k_{PB}\implies\frac{y_1}{x_1+8}=\frac{y_2}{x_2+8}\implies x_2y_1-x_1y_2=8(y_2-y_1)$
$$\begin{aligned}
S_{\Delta ABF}&=S_{\Delta PBF}-S_{\Delta PAF}=\frac{1}{2}|PF||y_1-y_2| \\
&=\frac{1}{2}\times 6\times |y_1-y_2|=\frac{3}{8}|x_1y_2-x_2y_1| \\
&\leq\frac{3}{8}\sqrt{12\times 16\times \left(\frac{x_1^2}{16}+\frac{y_1^2}{12}\right)\left[\frac{y_2^2}{12}+\frac{(-x_2)^2}{16}\right]}=3\sqrt{3}
\end{aligned}$$
当且仅当 $\displaystyle\frac{x_1x_2}{4}=-\frac{y_1y_2}{3}$ 时成立。
2. 【天津静海四校 2021 阶段性检测】已知 $\displaystyle E:\frac{x^2}{4}+y^2=1,A(-2,0),B(0,1),F_1(-\sqrt{3},0),F_2(\sqrt{3},0),P$ 为椭圆上一动点。$C,D$ 是 $E$ 上两个不同的点,$CD//AB$,直线 $CD$ 与 $x,y$ 轴分别交于 $M,N$ 两点,且 $\overrightarrow{MC}=\lambda\overrightarrow{CN},\overrightarrow{MD}=\mu\overrightarrow{DN}$,求 $\lambda+\mu$ 的取值范围。
显然 $\displaystyle k_{AB}=\frac{1}{2}$,可设 $CD$ 的方程为 $\displaystyle y=\frac{1}{2}x+m(m\neq\pm 1)$,得 $M(-2m,0),N(0,m)$,设 $C(x_1,y_1),D(x_2,y_2)$
由 $\overrightarrow{MC}=\lambda\overrightarrow{CN}$,得 $\displaystyle (x_1+2m,y_1)=\lambda(-x_1,m-y_1)\implies\begin{cases}\displaystyle x_1=\frac{-2m}{1+\lambda} \\\displaystyle y_1=\frac{\lambda m}{1+\lambda}\end{cases}$
代入椭圆方程并化简得 $(m^2-1)\lambda^2-2\lambda+m^2-1=0$,把 $\lambda$ 换成 $\mu$ 得到同构方程,因此 $\lambda,\mu$ 可看成 $(m^2-1)x^2-2x+m^2-1=0$ 的两根。
得到 $\displaystyle\lambda+\mu=\frac{2}{m^2-1}$,因为 $C,D$ 都在 $E$ 上,由柯西不等式
$$2=\left(\frac{x^2}{4}+y^2\right)[(-1)^2+1]\geq\left(-\frac{1}{2}x+y\right)^2=m^2$$
当且仅当 $C,D$ 重合时等号成立,与题意不符,故 $0\leq m^2<2$ 且 $m^2\neq 1$,所以 $\displaystyle\lambda+\mu=\frac{2}{m^2-1}\in(-\infty,-2]\cup(2,\infty)$.
#### $\text{Lagrange}$ 拉格朗日恒等式
##### 椭圆形式的拉格朗日恒等式
设 $A(x_1,y_1),B(x_2,y_2)$ 是椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上非顶点的两点,则:
$$1=\left(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}\right)\left(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}\right)=\left(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}\right)^2+\frac{(x_1y_2-x_2y_1)^2}{a^2b^2}$$
##### 引理 - 三角形面积公式
$\overrightarrow{OA}=(x_1,y_1),\overrightarrow{OB}=(x_2,y_2)$,则 $\displaystyle S_{\Delta OAB}=\frac{1}{2}|x_1y_2-x_2y_1|$
因此,拉格朗日恒等式可用于处理三角形面积定值问题。当 $\displaystyle\left(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}\right)^2=0$ 时,$\displaystyle S_{\max}=\frac{ab}{2}$.
##### 引理 - 和积关系 & 合比关系
已知 $A(x_1,y_1),B(x_2,y_2)$ 在椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上,直线 $AB$ 经过 $M(m,0)$ 满足:
$$2x_1x_2=\left(\frac{a^2}{m}+m\right)(x_1+x_2)-2a^2$$
直线 $AB$ 经过 $N(0,n)$ 满足:
$$2y_1y_2=\left(\frac{b^2}{n}+n\right)(y_1+y_2)-2b^2$$
可用点差法证明。
##### 例题
1. 椭圆 $\displaystyle E:\frac{x^2}{16}+\frac{y^2}{4}=1,P(0,1),Q(0,2)$,过点 $P$ 的直线 $l:y=kx+1$ 交椭圆 $E$ 于 $A,B$ 两点,求 $S_{\Delta ABQ}$ 最大值。
由 $A,B,P$ 三点共线得 $\displaystyle\frac{y_1-1}{x_1}=\frac{y_2-1}{x_2}$,得
$$(1)\ \ \ \ \ x_1y_2-x_2y_1=x_1-x_2$$
$$(2)\ \ \ \ \ 2y_1y_2=5(y_1+y_2)-8$$
$$(3)\ \ \ \ \ x_1x_2=-6(y_1+y_2)$$
由 $(y_1+y_2)^2-(y_1-y_2)^2=4y_1y_2$ 和 $(2)$ 得 $(y_1+y_2)^2-(y_1-y_2)^2=10(y_1+y_2)-16$
配方得 $(y_1+y_2-5)^2=9+(y_1-y_2)^2\geq 9$
所以 $y_1+y_2\leq 2$ 当且仅当 $y_1=y_2=1$ 时成立( $y_1+y_2\geq 8$ 舍去 )
由拉格朗日恒等式得
$$\begin{aligned}
1&=\left(\frac{x_1x_2}{16}+\frac{y_1y_2}{4}\right)^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\
&=\left(\frac{y_1+y_2}{4}-1\right)^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\
&\geq \frac{1}{4}+\frac{(x_1y_2-x_2y_1)^2}{64}
\end{aligned}$$
得 $|x_1y_2-x_2y_1|\leq 4\sqrt{3}$,所以 $\displaystyle S=\frac{1}{2}|PQ||x_1-x_2|=\frac{1}{2}|x_1y_2-x_2y_1|\leq 2\sqrt{3}$
2. 已知椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$A,B$ 是其上两动点,$\displaystyle k_{OA}\cdot k_{OB}=-\frac{b^2}{a^2}$,点 $M$ 满足 $\overrightarrow{OM}=\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}$ 且 $\lambda^2+\mu^2=1$,证明 $M$ 在椭圆上。
设 $A(x_1,y_1),B(x_2,y_2)$,易得 $\displaystyle\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}=0$,点 $\displaystyle\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1,\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1$
因此 $M(\lambda x_1+\mu x_2,\lambda y_1+\mu y_2)$,代入椭圆方程联立得
$$\lambda^2\left(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}\right)+\mu^2\left(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}\right)+2\lambda\mu\left(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}\right)=1$$
得到 $\lambda^2+\mu^2=1$,结论成立。( 每一步都是等价关系 )
#### 参数方程
| 曲线方程 | 参数方程 | 三角消元 |
|:-:|:-:|:-:|
| 直线 $y-y_0=\tan\alpha(x-x_0)(\alpha$ 为倾斜角 $)$ | $\begin{cases}x=x_0+t\cos\alpha \\ y=y_0+t\sin\alpha\end{cases}(t$ 为参数 $)$ | $P(x_0+t\cos\alpha,y_0+t\sin\alpha)$ |
| 圆 $(x-a)^2+(y-b)^2=r^2(r>0)$ | $\begin{cases}x=r\cos\alpha+a \\ y=r\sin\alpha+b\end{cases}(\alpha$ 为参数 $)$ | $P(r\cos\alpha+a,r\sin\alpha+b)$ |
| 椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ | $\begin{cases}\displaystyle x=a\cos\alpha \\ \displaystyle y=b\sin\alpha\end{cases}(\alpha$ 为参数 $)$ | $P(a\cos\alpha,b\sin\alpha)$ |
| 双曲线 $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ | $\begin{cases}\displaystyle x=\frac{a}{\cos\alpha} \\ y=b\tan\alpha\end{cases}(\alpha$ 为参数 $)$ | $\displaystyle P\left(\frac{a}{\cos\alpha},b\tan\alpha\right)$ |
本质就是利用 $\sin^2\alpha+\cos^2\alpha=1$.
##### 例题
1. 过椭圆 $\displaystyle C:\frac{x^2}{4}+\frac{y^2}{9}=1$ 上一点 $P$ 作与直线 $l:2x+y-6=0$ 夹角为 $30\degree$ 的直线,交于 $A$,求 $|PA|$ 的最值。
设 $P(2\cos\theta,3\sin\theta)$,距离 $\displaystyle d(P,l)=\frac{\sqrt{5}}{5}|4\cos\theta+3\sin\theta-6|$,
则 $\displaystyle|PA|=\frac{d}{\sin 30\degree}=\frac{2\sqrt{5}}{5}|5\sin(\theta+\alpha)-6|$,其中 $\alpha$ 为锐角。所以最值为 $\displaystyle\frac{2\sqrt{5}}{5}$ 和 $\displaystyle\frac{22\sqrt{5}}{5}$.
2. 椭圆 $\displaystyle C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$A,B,C$ 为其上三点,满足 $\Delta ABC$ 的重心坐标为 $O$,求 $S_{\Delta ABC}$.
设 $A(a\cos\alpha,b\sin\alpha),B(a\cos\beta,b\sin\beta)\implies C(-a(\cos\alpha+\cos\beta),-b(\sin\alpha+\sin\beta))$,代入得
$\displaystyle(\cos\alpha+\cos\beta)^2+(\sin\alpha+\sin\beta)^2=2+2\cos\alpha\cos\beta+2\sin\alpha\sin\beta=2+2\cos(\alpha-\beta)=1\implies\cos(\alpha-\beta)=-\frac{1}{2}\implies\alpha-\beta=120\degree$
$|AB|=\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}$
$\displaystyle AB:y=\frac{b(\sin\alpha-\sin\beta)}{a(\cos\alpha-\cos\beta)}(x-a\cos\alpha)+b\sin\alpha\implies b(\sin\beta-\sin\alpha)x+a(\cos\alpha-\cos\beta)y+ab\sin(\alpha-\beta)=0$
$\displaystyle d(O,AB)=\frac{\frac{\sqrt{3}}{2}ab}{\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}}$
由重心性质,$\displaystyle S_{\Delta ABC}=3S_{\Delta AOB}=\frac{3}{2}|AB|d=\frac{3\sqrt{3}}{4}ab$.
- 扩展开来,对于平行四边形 $OABC$,其中 $A,B,C$ 三点都在椭圆上,则 $\displaystyle S=2S_{\Delta AOB}=\frac{\sqrt{3}}{2}ab$.
#### 圆锥曲线与四点共圆
前置知识:[here](https://zhuanlan.zhihu.com/p/695714852)
- 椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 上四边形 $ABCD$ 四点共圆 $\iff k_{AB}+k_{CD}=0$( 圆锥曲线均适用,**任选两组点**斜率相加 $=0$ 即可 )。若圆心为 $O(x_0,y_0)$,则四边形 $ABCD$ 重心坐标是 $\displaystyle G\left(\frac{1}{e^2}x_0,\left(1-\frac{1}{e^2}\right)y_0\right)$.
例 1:双曲线 $x^2-y^2=1,A(x_1,y_1),B(x_2,y_2),C(x_3,y_3),D(x_4,y_4)$ 共圆,求证 $(x_1+y_1)(x_2+y_2)(x_3+y_3)(x_4+y_4)$ 为定值。
设 $AB:my_1+t$,可以得到 $\displaystyle(x_1+y_1)(x_2+y_2)=-\frac{m_1+1}{m_1-1}$,同理 $\displaystyle(x_3+y_3)(x_4+y_4)=-\frac{m_2+1}{m_2-1}$,因 $m_1+m_2=0$,可以得出定值为 $1$.
---
例 2:$E:y^2=4x$,过 $F(1,0)$ 的动直线交 $E$ 于 $A,B$ 两点,$\Delta OAB$ 的外接圆交 $E$ 于 $C$,证明:$(1)\ \Delta ABC$ 的重心在定直线上;$(2)$ 若 $OACB$ 是凸四边形,求 $S_{OACB}$ 范围。
$\displaystyle (1)\ A(x_1,y_1),B(x_2,y_2),C(x_3,y_3),k_{AB}=\frac{4}{y_1+y_2},k_{OC}=\frac{4}{y_3}$,由结论得 $y_1+y_2+y_3=0$,即定直线 $y=0$.
$(2)$ 设 $AB:x=my+1,S_{OACB}=S_{OAB}+S_{ABC}=2\sqrt{m^2+1}(1+|8m^2-1|)$
因为凸四边形,不妨设 $y_1>0,y_2<0,y_3=-4m=-(y_1+y_2)<y_2$,而 $y_1y_2=-4$ 得 $\displaystyle y_2\in(-\sqrt{2},0),m^2>\frac{1}{8}$,所以 $S_{OACB}=16m^2\sqrt{m^2+1}$,范围 $\displaystyle\left(\frac{3\sqrt{2}}{2},+\infty\right)$.
例 3:【2022.8 ZJ 新高考研究测试卷】椭圆 $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 上三点 $A,B,C$ 构成三角形,$\Delta ABC$ 外心为 $D$,求证:当 $AB,BC,CA,OD$ 斜率存在时,$\red{\boxed{k_{AB}k_{BC}k_{CA}k_{OD}=\frac{b^2}{a^2}}}$
设 $AB,BC$ 中点分别为 $E(x_1,y_1),F(x_2,y_2),D(x_0,y_0)$,有
$$\begin{cases}k_{AB}k_{OE}=-\frac{b^2}{a^2}\\k_{AB}k_{DE}=-1\end{cases}\implies \frac{k_{OE} }{k_{DE} }=\frac{b^2}{a^2}=\frac{\frac{y_1}{x_1} }{\frac{y_1-x_0}{x_1-x_0} }={\frac{x_1y_1-x_0y_1}{x_1y_1-x_1y_0} }$$
$$\implies\begin{cases}(a^2-b^2)x_1y_1=a^2x_0y_1-b^2x_1y_0\\(a^2-b^2)x_2y_2=a^2x_0y_2-b^2x_2y_0\end{cases}\implies\begin{cases}(a^2-b^2)x_1y_1x_2y_2=a^2x_0x_2y_1y_2-b^2x_1y_0x_2y_2\\(a^2-b^2)x_1x_2y_1y_2=a^2x_0x_1y_1y_2-b^2x_1y_0x_2y_1\end{cases}$$
$$\implies 0=a^2x_0y_1y_2(x_2-x_1)-b^2x_1x_2y_0(y_2-y_1)\implies \frac{b^2}{a^2}=\frac{x_0y_1y_2(x_2-x_1)}{y_0x_1x_2(y_2-y_1)}=\frac{k_{OE}k_{OF}}{k_{OD}k_{AC}}=\frac{(-\frac{b^2}{a^2})^2}{k_{AB}k_{BC}k_{CA}k_{OD}}$$
类似可以推出双曲线满足 $\red{\boxed{k_{AB}k_{BC}k_{CA}k_{OD}=-\frac{b^2}{a^2}}}$,抛物线满足 $\red{\boxed{\frac{1}{k_1^2}+\frac{1}{k_2^2}+\frac{1}{k_3^2}+\frac{2}{k_1k_2k_3k_4}=-2}}$
例 4:【2021 I 卷】在平面直角坐标系 $xOy$ 中,已知点 $F_1(-\sqrt{17},0),F_2(\sqrt{17},0),|MF_1|-|MF_2|=2$,点 $M$ 的轨迹为 $C$。
$(1)$ 求 $C$ 的方程。答案:$\displaystyle x^2-\frac{y^2}{16}=1(x\geq 1)$
$(2)$ 设点 $T$ 在直线 $\displaystyle x=\frac{1}{2}$ 上,过 $T$ 的两条直线分别交 $C$ 于 $A,B$ 两点和 $P,Q$ 两点,且 $|TA|\cdot|TB|=|TP|\cdot|TQ|$,求直线 $AB$ 的斜率和直线 $PQ$ 的斜率之和。
当然此题硬解可做。不过更快的是由圆幂定理可知 $A,B,P,Q$ 四点共圆,于是答案为 $0$.
设 $\displaystyle T\left(\frac{1}{2},t\right),AB:y-t=k_1\left(x-\frac{1}{2}\right),PQ:y-t=k_2\left(x-\frac{1}{2}\right)$,则二次曲线
$$\left(k_1x-y-\frac{k_1}{2}+t\right)\left(k_2x-y-\frac{k_2}{2}+t\right)=0$$
又有 $\displaystyle x^2-\frac{y^2}{16}=1$,得到过 $A,B,P,Q$ 的二次曲线系方程为
$$\lambda\left(k_1x-y-\frac{k_1}{2}+t\right)\left(k_2x-y-\frac{k_2}{2}+t\right)+\mu\left(x^2-\frac{y^2}{16}-1\right)=0\ \ \ \ (\lambda\neq 0)$$
其中 $xy$ 项的系数为 $-\lambda(k_1+k_2)$,由于共圆,于是该系数为 $0$,得到 $k_1+k_2=0$.
---
练:【保定一模】椭圆 $\displaystyle\frac{x^2}{8}+\frac{y^2}{4}=1$,过右焦点 $F$ 作不与 $F$ 垂直的直线 $l$ 交椭圆于 $A,B$ 两点。$AB$ 的中垂线交 $x$ 轴于点 $M$,交直线 $x=4$ 于点 $N$,直线 $x=4$ 与 $x$ 轴交于点 $H$。证明 $A,M,B,N,C$ 五点共圆。( 原题不要求证 $C$ 点在圆上 )
#### 曲线系
定义:具有一系列性质相似的曲线( 包括直线 )的集合,并且可以通过参数进行调整。
例如:平行直线系:$Ax+By+\lambda=0$,过定点的直线系 $\lambda(A_1x+B_1y+C_1)+\mu(A_2x+B_2y+C_2)=0$,圆的切线系 $x\cos\theta+y\sin\theta=r$,同离心率椭圆 / 双曲线系:$\displaystyle\frac{x^2}{a^2}\pm\frac{y^2}{b^2}=k$.
##### 求曲线系方程
1. 过圆 $x^2+y^2+Dx+Ey+F=0$ 和直线 $Ax+By+C=0$ 的圆系方程:$$x^2+y^2+Dx+Ey+F+\lambda(Ax+By+C)=0$$
2. 过圆 $C_1:x^2+y^2+D_1x+E_1y+F_1=0$ 和 $C_2:x^2+y^2+D_2x+E_2y+F_2=0$ 的公共交点的圆的圆系方程:( $\lambda=-1$ 时为公共弦方程 )$$x^2+y^2+D_1x+E_1y+F_1+\lambda(x^2+y^2+D_2x+E_2y+F_2)=0$$
3. 与直线 $Ax+By+C=0$ 相切于点( 或圆 )$M(x_0,y_0)$ 的圆系方程:$$(x-x_0)^2+(y-y_0)^2+\lambda(Ax+By+C)=0$$
4. 与直线 $x^2+y^2+Dx+Ey+F=0$ 相切于点( 或圆 )$M(x_0,y_0)$ 的圆系方程:( $\lambda\neq -1$ )$$(x-x_0)^2+(y-y_0)^2+\lambda(x^2+y^2+Dx+Ey+F=0)=0$$
##### 定理
以下记 $l_{AB}(x,y)=0$ 表示直线 $AB:Ax+By+C=0$,记 $C(x,y)=0$ 表示二次曲线 $Ax^2+By^2+Dx+Ey+F=0$。
引理 1:方程 $l_1(x,y)\cdot l_2(x,y)=0$ 表示两条直线上的所有点。
引理 2:平面上不共线的五点确定一个二次曲线。
定理 1:$C_1(x,y)=0,C_2(x,y)=0$,如果有四个交点,则四点共圆。
证明:构造 $\lambda C_1(x,y)+\mu C_2(x,y)=0$,取 $\displaystyle\frac{\lambda}{\mu}=-\frac{A_2-B_2}{A_1-B_1}$ 让系数相同,表示一个圆。
定理 2:取 $C(x,y)$ 上一点 $P$,过该点作斜率为 $k_1,k_2$ 的直线,分别交 $C$ 于 $M,N$ 两点( 异于 $P$ ),则
- 若 $k_1+k_2=0$,则 $MN$ 斜率为定值。
- 若 $k_1k_2$ 为定值,则 $MN$ 过定点。
证明:设 $P(x_0,y_0)$,切线 $\displaystyle Ax_0x+By_0y+D\frac{x_0+x}{2}+E\frac{y_0+y}{2}+F=0$
写出 $l_{PM}:k_1x-y-k_1x_0+y_0=0,l_{PN}:k_2x-y-k_2x_0+y_0=0,l_{MN}:kx-y+b=0$
写出曲线系方程:$\displaystyle\lambda\left[\left(Ax_0+\frac{D}{2}\right)x+\left(By_0+\frac{E}{2}\right)y+\left(\frac{Dx_0+Ey_0}{2}+F\right)\right][kx-y+b]+\mu[k_1x-y-k_1x_0][k_2x-y-k_2x_0+y_0]=Ax^2+By^2+Dx+Ey+F=0$,比较系数得
| $\displaystyle x^2:A=\lambda\left(Ax_0+\frac{D}{2}\right)+\mu k_1k_2$ | $\displaystyle xy:0=\lambda\left[-\left(Ax_0+\frac{D}{2}\right)+k\left(By_0+\frac{E}{2}\right)\right]-\mu(k_1+k_2)$ |
|:-:|:-:|
| $\displaystyle y^2:B=-\lambda\left(By_0+\frac{E}{2}\right)+\mu$ | $\displaystyle 1:F=\lambda b\left(\frac{Dx_0+Ey_0}{2}+F\right)+\mu(y_0-k_1x_0)(y_0-k_2x_0)$ |
使用 $x^2,y^2$ 的表达式解出 $\lambda,\mu$,使用 $xy$ 的表达式解出 $k_1+k_2$,并将 $\lambda,\mu$ 代入。发现:
- 当 $k_1+k_2=0$ 时,$k$ 为定值。
- 整理第四个式子得到 $\displaystyle F=\lambda b\left(\frac{Dx_0+Ey_0}{2}+F\right)+\mu[y_0^2+k_1k_2x_0^2-(k_1+k_2)x_0y_0]$,把你已知的全部代入即可得到定点。
##### 例题
首先说明:应用曲线系求方程**一定要检验**!!!
1. 已知曲线 $y=5-x^2$ 与 $y=\displaystyle\frac 1 x$ 交于 $A,B,C$ 三点,则 $\Delta ABC$ 的外接圆方程为 ?
$y=5-x^2\implies y^2=5y-x^2y=5y-x$,再与 $x^2=5-y$ 相加得到 $x^2+y^2+x-4y-5=0$
---
2. 求与圆 $x^2+y^2-4x-8y+15=0$ 切于 $(3,6)$ 且过点 $(5,6)$ 的圆的方程。
$$x^2+y^2-4x-8y+15+\lambda[(x-3)^2+(y-6)^2]=0$$
将 $(5,6)$ 代入得到 $\lambda=-2$,检验得知其满足条件。
---
3. $A,B$ 是双曲线 $\displaystyle x^2-\frac{y^2}{2}=\lambda(\lambda\neq 0)$ 上两点,$N(1,2)$ 是 $AB$ 中点,$AB$ 的中垂线与双曲线交于 $C,D$ 两点,试判断 $ABCD$ 是否共圆并说明理由。
首先可以得到 $l_{AB}:y=x+1,l_{CD}:y=3-x$,则过 $ABCD$ 的圆可以表示为 $$(x-y+1)(x+y-3)+t\left(x^2-\frac{y^2}{2}-\lambda\right)=0\implies (1+t)x^2-\left(1+\frac{t}{2}\right)y^2-2x+4y+3-t\lambda=0$$
若共圆则 $\displaystyle 1+t=-1-\frac{t}{2}\neq 0\implies t=-\frac{3}{4}$,检验得知符合题意。
---
4. $B(0,1),P,Q$ 为椭圆 $\displaystyle \frac{x^2}{4}+y^2=1$ 上异于 $B$ 的两点且 $BP\perp BQ$,若 $B$ 在 $PQ$ 上的射影为 $M$,求 $M$ 的轨迹方程。
设 $\displaystyle BP:y=kx+1,BQ:y=-\frac{x}{k}+1$,则过 $BPQ$ 的二次曲线系方程为 $$(kx-y-1)\left(-\frac{1}{k}x+y-1\right)+\lambda\left(\frac{x^2}{4}+y^2-1\right)=0$$
由于其包含 $B$ 处的切线,将 $y=1$ 代入得 $\lambda=-4$,进一步得到 $\displaystyle (y-1)\left[\left(k-\frac{1}{k}\right)x-5y-3\right]=0$,故 $\displaystyle PQ:\left(k-\frac{1}{k}\right)x-5y-3=0$,则 $PQ$ 过定点 $\displaystyle \left(0,-\frac{3}{5}\right)$,故 $M$ 的轨迹为以 $BN$ 为半径的圆( 除去点 $B$ ):
$$x^2+\left(y-\frac{1}{5}\right)^2=\frac{16}{25}\ \ (y\neq 1)$$
---
5. 【2015 SN】( 表述经修改 )设 $E:\displaystyle\frac{x^2}{2}+y^2=1,A(0,-1)$,经过点 $(1,1)$ 且斜率为 $k$ 的直线与 $E$ 交于不同的两点 $P,Q$( 均异于点 $A$ ),证明:$k_{AP}+k_{AQ}=2$.
设 $AP:k_1x-y-1=0,AQ:k_2x-y-1=0,PQ:kx-y+1-k=0$,点 $A$ 切线 $y+1=0$,则设
$$(k_1x-y-1)(k_2x-y-1)+\lambda(y+1)(kx-y+1-k)=0\\\implies k_1k_2x^2+(\lambda k-k_1-k_2)xy+(1-\lambda)y^2+(\lambda k-k_1-k_2)x+(2-\lambda k)y+1+\lambda(1-k)=0$$
由于该曲线系为椭圆 $E$,比对系数得到 $k_1+k_2=2$.
# 数列
- 等差数列通项公式:$a_n=a_1+(n-1)d=S_n-S_{n-1}(n\geq 2)$, 其中 $d$ 为公差。
- 等差数列前 $n$ 项和:$\displaystyle S_n=\frac{n(a_1+a_n)}{2}=na_1+\frac{dn(n-1)}{2}$
- 等比数列通项公式:$a_n=a_1q^{n-1}=S_n-S_{n-1}(n\geq 2)$, 其中 $q$ 为公比。
- 等比数列前 $n$ 项和:$\displaystyle S_n=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_n q}{1-q}(q\neq 1)$
- 自然数幂求和公式:$\displaystyle\sum_{i=1}^{n}i=\frac{n(n+1)}{2}\ \ \ \ \ \ \ \ \ \sum_{i=1}^{n}i^2=\frac{n(n+1)(2n+1)}{6}$
$\displaystyle\sum_{i=1}^{n}i^3=\left[\frac{n(n+1)}{2}\right]^2=\left(\sum_{i=1}^n i\right)^2\ \ \ \ \ \ \ \ \ \sum_{i=1}^{n}i^4=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}$
$1+3+5+\dots+(2n-1)=n^2$
## 求数列通项公式
#### 累加法
条件:形如 $a_{n+1}=a_n+f(n)$ 且 ${f(n)}$ 可求和。
例题:已知 $a_1=1,a_{n+1}=a_n+2$,求 ${a_n}$ 通项公式。
由已知得 $a_{n+1}-a_n=2,a_n-a_{n-1}=2,\dots,a_2-a_1=2$,将它们全部相加得到 $a_{n+1}-a_1=a_{n+1}-1=2n$,即 $a_{n}=2n-1$。
验证 $a_1$ 也符合上式,因此 $a_n=2n-1$.
练习:已知 $\set{a_n}$ 满足 $a_1=2,a_{2020}=2020,na_{n-1}+n(n-1)a_{n+1}=(n-1)a_n,n\in\N^*,n>1$. 求 $S_3$ 和 $S_{2021}$.
答案都是 $3$.
#### 累乘法
形如 $a_{n+1}=f(n)a_n$ 且 ${f(n)}$ 可求积。
例题:$a_1=1,(n+1)a_{n+1}=na_n$,求 ${a_n}$ 通项公式。
$$\frac{a_{n+1}}{a_n}=\frac{n}{n+1}\implies a_n=\frac{a_n}{1}=\frac{a_n}{a_1}=\frac{a_n}{a_{n-1}}\frac{a_{n-1}}{a_{n-2}}\dots\frac{a_2}{a_1}=\frac{n-1}{n}\frac{n-2}{n-1}\dots\frac{1}{2}=\frac{1}{n}$$
验证 $a_1$ 也符合上式,因此 $\displaystyle a_n=\frac{1}{n}$.
#### 利用 $a_n=S_n-S_{n-1}$
例题:$S_n=3^n+k$,求 $a_n$ 通项公式。
$a_1=3+k,\ \ a_n=S_n-S_{n-1}=3^n-3^{n-1}=2\times 3^{n-1}$
## 裂项
以下是一些基本的小学奥数难度的裂项。
$$a^2-a+1=\frac{a^4+a^2+1}{a^4+a+1}$$
$$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$$
$$\frac{1}{n(n+1)(n+2)}=\frac{1}{2}\left[\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)}\right]$$
$$\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right)$$
$$\frac{1}{\sqrt{a}+\sqrt{b} }=\frac{1}{a-b}\left(\sqrt{a}-\sqrt{b}\right)$$
$$\frac{1}{a_na_{n+k} }=\frac{1}{dk}\left(\frac{1}{a_n}-\frac{1}{a_{n+k} }\right)\ \ \ \ ( 等差数列 )$$
$$\frac{2^n}{(2^n+1)(2^{n+1}+1)}=\frac{1}{2^n+1}-\frac{1}{2^{n+1}+1}$$
$$\frac{q^n}{(q^{n+1}+1)(q^n+1)}=\frac{1}{q-1}\left(\frac{1}{q^n+1}-\frac{1}{q^{n+1}+1}\right)$$
- 一个特点:前面保留几项,后面就保留几项。例如
$$\sum_{k=1}^n \frac{1}{k(k+2)}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\dots+\frac{n}{1}-\frac{1}{n+2})=\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$$
练习:已知 $\set{a_n}$ 是首项为 $1$,公比为 $\frac{1}{2}$ 的等比数列,证明:$\forall n\in\N^*$,$$\frac{2a_2}{S_1S_2}+\frac{2a_3}{S_2S_3}+\dots+\frac{2a_{n+1}}{S_nS_{n+1}}<1-\frac{1}{2^{n+1}}$$
现在我们要学习一些高难度的裂项。坐稳了,前方高能!
$$\sqrt{1+\frac{1}{k^2}+\frac{1}{(k+1)^2} }=1+\frac{1}{k}-\frac{1}{k+1}$$
$$\frac{k}{(2k+1)^2(2k-1)^2}=\frac{1}{8}\left(\frac{1}{(2k-1)^2}-\frac{1}{(2k+1)^2}\right)$$
$$\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k} }=\frac{1}{\sqrt{k} }-\frac{1}{\sqrt{k+1} }$$
$$\sum_{k=1}^n k!(k^2+k+1)=\sum_{k=1}^n [(k+1)!(k+1)-k!k]=(n+1)!(n+1)-1$$
$$\sum_{k=1}^n \frac{k^2+k-1}{(k+2)!}=\sum_{k=1}^n \left(\frac{k}{(k+1)!}-\frac{k+1}{(k+2)!}\right)=\frac{1}{2}-\frac{n+1}{(n+2)!}$$
$$\frac{3k^2-1}{(k^3-k)^2}=\frac{k-\frac{1}{2} }{k^2(k-1)^2}-\frac{k+\frac{1}{2} }{k^2(k+1)^2}$$
$$\frac{4k}{4k^4+1}=\frac{1}{2k^2-2k+1}-\frac{1}{2k^2+2k+1}$$
$$\frac{1}{\sqrt{k+\sqrt{k^2-1}}}=\frac{\sqrt{k+1}\ \ \xcancel{-\sqrt{k}+\sqrt{k}}-\sqrt{k-1}}{\sqrt{2}}$$
## 等差数列的性质
- $\displaystyle\frac{S_n}{n}=\frac{na_1+\frac{n(n-1)d}{2}}{n}=a_1+\frac{n-1}{2}d$,则 $\displaystyle\frac{S_n}{n}$ 是首项为 $a_1$,公差为 $\displaystyle\frac{d}{2}$ 的等差数列。
- 若等差数列的项数为 $2n$,则 $S_{2n}=n(a_n+a_{n+1})$,且 $\displaystyle S_{偶}-S_{奇}=nd,\frac{S_{奇}}{S_{偶}}=\frac{a_n}{a_{n+1}}$
- 若等差数列的项数为 $2n-1$,则 $S_{2n-1}=(2n-1)a_n$,且 $\displaystyle S_{偶}-S_{奇}=a_n,\frac{S_{奇}}{S_{偶}}=\frac{n}{n-1}$
- 等差数列依次每 $k$ 项之和仍成等差数列,即 $S_k,S_{2k}-S_k,S_{3k}-S_{2k},\dots,S_{nk}-S_{(n-1)k}$ 成等差数列,公差 $k^2d$.
- $\displaystyle S_{2n-1}=\frac{(2n-1)(a_1+a_{2n-1})}{2}=(2n-1)a_n,a_n=\frac{S_{2n-1}}{2n-1}$.
- 等差数列 ${a_n},{b_n}$ 的前缀和分别为 $S_n,T_n$,则 $\displaystyle\red{\boxed{\frac{a_n}{b_n}=\frac{S_{2n-1}}{T_{2n-1}}}}$.
- $\displaystyle S_m=p,S_n=q\implies \red{\boxed{S_{n+m}=\frac{(S_n-S_m)(n+m)}{n-m}}}=\frac{(q-p)(n+m)}{n-m}$
特别的,若 $S_m=n,S_n=m$,则 $S_{n+m}=-(n+m)$;若 $S_n=S_m$,则 $S_{n+m}=0$。
## 等比数列的性质
- 若 $m+n=r+s(m,n,r,s\in\N^+)$,则 $a_ma_n=a_ra_s$.
- ${a_n}$ 公比为 $q\implies \lambda a_n$ 公比为 $q$,$\displaystyle\frac{1}{a_n}$ 公比为 $\displaystyle\frac{1}{q}$,$|a_n|$ 公比为 $|q|$,$\lg a_n$ 公比为 $\lg q$,$a_n\pm a_{n+1}$ 公比为 $q$;若 $b_n$ 公比为 $q'$,则 $a_nb_n$ 公比为 $qq'$.
**注意 $q=\pm 1$ 是否满足条件**。
- $a_n$ 的前 $n$ 项积记为 $\displaystyle T_n=a_1^n q^{\frac{n(n-1)}{2}}$,且 $\displaystyle T_n,\frac{T_{2n}}{T_n},\frac{T_{3n}}{T_{2n}}$ 为公比 $=q^{n^2}$ 的等比数列,由此可得 $\displaystyle T_{3n}=\left(\frac{T_{2n}}{T_n}\right)^3$.
### 构造等比数列求通项公式
- 对于 $a_n=pa_{n-1}+q(p\neq 1,pq\neq 0,n\geq 2)$,转化为 $$a_n-\frac{q}{1-p}=p\left(a_{n-1}-\frac{q}{1-p}\right)\implies a_n=(a_1+x)p^{n-1}-x$$
其中 $\displaystyle x=\frac{q}{p-1}$. 记不住怎么办 ?我们利用特征根法,解方程 $x=px+q$ 即可。
也可以通过与 $a_{n-1}=pa_{n-2}+q$ 相减得 $a_n-a_{n-1}=p(a_{n-1}-a_{n-2})$
- 对于 $\displaystyle a_n=pa_{n-1}+q^{n-1}$,转化为 $\displaystyle a_n-\frac{q^n}{q-p}=p\left(a_{n-1}-\frac{q^{n-1}}{q-p}\right)$
也可以同除 $q^n$ 变成上一点的方法。
- 对于 $a_n=pa_{n-1}+q^{n-1}+t$,转化为 $\displaystyle a_n-\frac{t}{1-p}=p\left(a_{n-1}-\frac{t}{1-p}\right)+q^{n-1}$,再用上一点的方法。
## 数列的快算方法
大题基本禁用,小题屡试不爽的方法。
#### 等差数列 / 等比数列 $S_0=0$
例题:等比数列 $\set{a_n}$ 的 $S_n=a\cdot 2^{n-1}+a-2$,求 $a$.
直接代入 $S_0=\frac{3}{2}a-2=0$ 得 $\displaystyle a=\frac{4}{3}$.
练习:已知数列 $\set{a_n}$ 的 $S_n=3^n+k$,以下正确的是( $\ \ \ \ \text{}$ )
$\text{A.}\ k$ 为任意实数时,$\set{a_n}$ 为等比数列。 $\text{B.}\ k=-1$ 时,$\set{a_n}$ 是等比数列。
$\text{C.}\ k=0$ 时,$\set{a_n}$ 是等比数列。$\ \ \ \ \ \ \ \ \ \ \text{D.}\ \set{a_n}$ 不可能是等比数列。
选 $\text{B}$.
#### 一个条件的数列选填
- 我们直接**令数列为常数数列**即可。
例:等差数列 $S_9=72$,求 $a_2+a_4+a_9$ 的值。答案:$24$.
#### 等差 $\times$ 等比 快速求和
- 若 $a_n=(An+B)q^{\red{n-1}}$,令 $\red{\boxed{D=\frac{A}{q-1},E=\frac{B-D}{q-1}}}$,则 $\red{\boxed{S_n=(Dn+E)q^n-E}}$.
证明:错位相减。
例题:$\displaystyle a_n=\frac{n}{3^n}$,求 $S_n$.
首先写成这样:$\displaystyle a_n=\frac{1}{3}n\left(\frac{1}{3}\right)^{n-1}$,然后 $\displaystyle D=-\frac{1}{2},E=-\frac{3}{4},S_n=\left(-\frac{1}{2}n-\frac{3}{4}\right)\left(\frac{1}{3}\right)^n+\frac{3}{4}$.
错位相减法:
$$\begin{aligned}S_n=&\frac{1}{3}+\frac{2}{9}+\frac{3}{27}+\dots+\frac{n-1}{3^{n-1} }+\frac{n}{3^n}\\ 3S_n=1+&\frac{2}{3}+\frac{3}{9}+\dots+\frac{n-1}{3^{n-2} }+\frac{n}{3^{n-1} }\end{aligned}$$
$$\begin{aligned}2S_n&=1+\frac{1}{3}+\frac{1}{9}+\dots+\frac{1}{3^{n-1} }-\frac{n}{3^n}\\&=\frac{1-\frac{1}{3^n} }{\frac{2}{3} }-\frac{n}{3^n}=\frac{3}{2}-\frac{3}{2}\left(\frac{1}{3}\right)^n-n\left(\frac{1}{3}\right)^n\end{aligned}$$
练习 1:$a_n=(n+3)\cdot 2^{n-1}$,求 $S_n$.
练习 2:$a_n=2n+1,b_n=a_n\cdot 2^{a_n}$,求数列 $\set{b_n}$ 的 $S_n$.
练习 3:$a_n=4n-1=4\log_2 b_n+3$,求数列 $\set{a_n\cdot b_n}$ 的 $S_n$.
答案:$\displaystyle (1)\ S_n=(n+2)2^n-2\ \ (2)\ S_n=\left(\frac{16}{9}n+\frac{8}{9}\right)4^n-\frac{8}{9}\ \ (3)S_n=(4n-5)2^n+5$
#### 等差数列中的符号问题
$$\red{\boxed{a_n>0\implies S_{2n-1}>0\ \ \ \ \ \ \ \ \ \ \ \ a_n<0\implies S_{2n-1}<0}}$$
$$\boxed{a_n+a_m>0\implies S_{n+m-1}>0}$$
证明:$\displaystyle S_{2n-1}=\frac{a_1+a_{2n-1}}{2}(2n-1)=\frac{2a_n}{2}(2n-1)=a_n(2n-1)>0$
例题:已知 $\set{a_n}$ 为等差数列,$a_1>0$,若 $\displaystyle\frac{a_{1004}}{a_{1005}}<-1$,则使得 $S_n>0$ 的最大 $n$ 值为 ?
可以得到 $a_{1004}>0,a_{1005}<0,a_{1004}+a_{1005}>0$,那么答案为 $2008$.
练习:等差数列 $S_8<S_{10}<S_9$,则使得 $S_n>0$ 的最大 $n$ 值为 ?
答案:$18$.
$$a_{10}<0,S_{10}-S_8=a_{10}+a_9>0,a_9>0\implies S_{17}>0,S_{18}>0,S_{19}<0$$
#### 等差数列的最值
$$S_n=\frac{d}{2}n^2+\left(a_1-\frac{d}{2}\right)n$$
- 显然当 $\red{\boxed{n=\left[\frac{1}{2}-\frac{a_1}{d}\right]}}$ 时取最值。$[x]$ 表示将 $x$ 四舍五入后的值。
若 $S_p=S_q$,则 $S_n$ 函数的对称轴为 $\displaystyle\frac{p+q}{2}$.
若 $S_p=0$,则 $S_n$ 函数的对称轴为 $\displaystyle\frac{p}{2}$.
例:已知等差数列 $\displaystyle a_1>0,\frac{a_6}{a_5}=\frac{9}{11}$,求 $S_n$ 最大时 $n$ 的值。
整理得 $\displaystyle\frac{a_1}{d}=-\frac{19}{2},n=10$ 取最值。
#### 求数列通项的最值
解不等式 $\begin{cases}a_n\geq a_{n+1}\\a_n\geq a_{n-1}\end{cases}$ 或 $\begin{cases}a_n\leq a_{n+1}\\a_n\leq a_{n-1}\end{cases}$ 即可。
例:求数列 $\displaystyle a_n=n(n+4)\left(\frac{2}{3}\right)^n$ 的最大项。
解 $\begin{cases}\displaystyle n(n+4)\left(\frac{2}{3}\right)^n\geq (n+1)(n+5)\left(\frac{2}{3}\right)^{n+1}\\\displaystyle n(n+4)\left(\frac{2}{3}\right)^n\geq (n-1)(n+3)\left(\frac{2}{3}\right)^{n-1}\end{cases}$ 得 $\sqrt{10}\leq n\leq\sqrt{10}+1$,即 $n=4$.
练:求数列 $\displaystyle a_n=(n+1)\left(\frac{7}{8}\right)^n$ 的最大项。答案:$6$ 或 $7$.
#### 一类证明问题
- 要证明 $S_n<T_n$,而 $T_0=0$,则只需证明 $a_n<T_n-T_{n-1}$. 大于号同理。
其实跟下面要讲的数学归纳法很像。
例 1:$\displaystyle a_n=\sqrt{\frac{n(n+1)}{2}}$,证明 $\displaystyle S_n>\frac{n(n+1)}{2\sqrt{2}}$.
$\displaystyle T_n=\frac{n(n+1)}{2\sqrt{2}},T_0=0$ 因此只需证明 $\displaystyle a_n>T_n-T_{n-1}=\frac{n}{\sqrt{2}}$. 读者自证不难。
例 2:证明 $\displaystyle\left(1+\frac{1}{1}\right)\left(1+\frac{1}{3}\right)\left(1+\frac{1}{5}\right)\dots\left(1+\frac{1}{2n-1}\right)>\sqrt{2n+1}$.
**两边取对数**得 $\displaystyle\ln\left(1+\frac{1}{1}\right)+\ln\left(1+\frac{1}{3}\right)+\dots+\ln\left(1+\frac{1}{2n-1}\right)>\ln\sqrt{2n+1}$.
当 $n=0$ 时 $\ln\sqrt{2\times 0+1}=0$,因此只需证明
$$\ln\left(1+\frac{1}{2n-1}\right)>\ln\sqrt{2n+1}-\ln\sqrt{2n-1}=\frac{1}{2}\ln\frac{2n+1}{2n-1}$$
也即证明 $\displaystyle\left(\frac{2n}{2n-1}\right)^2>\frac{2n+1}{2n-1}$,读者自证不难。
练习 1:证明 $\displaystyle 2(\sqrt{n+1}-1)<\sum_{k=1}^n\frac{1}{\sqrt{k}}<2\sqrt{n}$.
练习 2:证明 $\displaystyle\sum_{k=2}^{n+1}\frac{1}{k}<\ln(n+1)<\sum_{k=1}^n\frac{1}{k}$.
练习 2 需要用导数中 $\ln(1+x)<x,\ln(1-x)<-x$ 的知识。
## 特征根
用于求解二阶线性递推数列的通项公式。对于形如 $a_{n+1}=pa_n+qa_{n-1}$,则方程 $x^2-px-q=0$ 为该数列的特征方程,方程的两个根 $a,b$ 即为数列的特征根。
当 $a\neq b$ 时,设数列 $a_n=\alpha a^{n-1}+\beta b^{n-1}$,由 $\begin{cases}a_1=\alpha+\beta\\a_2=\alpha a+\beta b\end{cases}$ 解出 $\alpha,\beta$ 即可。
需要注意的是 $a=b$ 时,数列应设为 $a_n=(\alpha+n\beta)a^n$.
例题:Fibonacci 数列满足 $a_1=a_2=1,a_{n+2}=a_{n+1}+a_n$,求通项公式。
特征方程 $x^2-x-1=0$ 得到 $\displaystyle x_1=\frac{1+\sqrt{5}}{2},x_2=\frac{1-\sqrt{5}}{2}$.
设 $a_n=Ax_1^n+Bx_2^n$,联立 $a_1=a_2=1$ 得 $\displaystyle A=B=\frac{1}{\sqrt{5}}$,故
$$a_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$$
另外 Fib 数列的性质:( $a_1=a_2=1,a_{n+2}=a_{n+1}+a_n$ )
1. $$a_{1}+a_2+\dots+a_n=a_{n+2}-1$$
$$(a_3-a_2)+(a_4-a_3)+\dots+(a_{n+2}-a_{n+1})=RHS$$
2. $$a_1+a_3+a_5+\dots+a_{2n-1}=a_{2n}$$
$$a_1+(a_4-a_2)+(a_6-a_4)+\dots+(a_{2n}-a_{2n-2})=RHS$$
3. $$a_2+a_4+a_6+\dots+a_{2n}=a_{2n+1}-1$$
$$(a_3-a_1)+(a_5-a_3)+(a_7-a_5)+\dots+(a_{2n+1}-a_{2n-1})=RHS$$
4. $$a_1^2+a_2^2+\dots+a_n^2=a_na_{n+1}$$
不断对右侧展开,和左边抵消就可以证明。
5. $$a_{n+2}a_n-a_{n+1}^2=(-1)^{n+1}$$
#### 一种数列处理技巧
例:$a_1=1,a_2=1,a_3=2$,有递推式 $a_na_{n+3}=3+a_{n+1}a_{n+2}$,求通项公式。
我们由递推式还可以得到 $a_{n+1}a_{n+4}=3+a_{n+2}a_{n+3}$,联立两式消掉 $3$ 得
$$a_na_{n+3}-a_{n+1}a_{n+4}=a_{n+1}a_{n+2}-a_{n+2}a_{n+3}$$
$$\implies(a_n+a_{n+2})a_{n+3}=a_{n+1}(a_{n+2}+a_{n+4})$$
$$\implies\frac{a_n+a_{n+2} }{a_{n+1} }=\dots=\frac{a_1+a_3}{a_2}=3$$
$$\implies a_{n+2}-3a_{n+1}+a_n=0$$
特征根解出 $\displaystyle a_n=A\left(\frac{3+\sqrt{5}}{2}\right)^n+B\left(\frac{3-\sqrt{5}}{2}\right)^n$,再代入 $a_1,a_2$ 得 $\displaystyle A=\frac{5-2\sqrt{5}}{5},B=\frac{5+2\sqrt{5}}{5}$.
练:$a_1=a_2=1,a_3=3,a_na_{n-2}=a_{n-1}^2+2$,求通项公式。
有 $\displaystyle\frac{a_{n+1}+a_{n-1}}{a_n}=\dots=\frac{a_1+a_3}{a_2}=4$,之后同上。
例 2:$a_0=0,a_{n+1}=3a_n+\sqrt{8a_n^2+1}$,求通项公式。
$$a_{n+1}^2-6a_{n+1}a_n+a_n^2-1=0$$
$$a_{n-1}^2-6a_{n-1}a_n+a_n^2-1=0$$
所以 $a_{n-1},a_{n+1}$ 是方程 $x^2-6a_nx+a_n^2-1=0$ 的两个根,得 $a_{n-1}+a_{n+1}=6a_n$.
答案:$\displaystyle a_n=\frac{\sqrt{2}}{8}(3+2\sqrt{2})^n-\frac{\sqrt{2}}{8}(3-2\sqrt{2})^n$.
【2024 HB 邢台二模】若数列 $\set{a_n}$ 满足递推关系 $a_{n+k}=c_1a_{n+k-1}+c_2a_{n+k-2}+\dots+c_ka_n(k\geq 2)(*)$ 其中 $c_i(i=1,2,\dots,k)$ 为常数,我们称该数列为 $k$ 阶常系数齐次线性递推数列,并称方程 $x^k=c_1x^{k-1}+\dots+c_k$ 为递推关系式 $(*)$ 的特征方程,该方程的根称为 $\set{a_n}$ 的特征根。我们有以下结论:对于 $k$ 阶常系数齐次线性递推数列,若其不同的特征根为 $x_1,x_2,\dots,x_s(s\leq k)$,且特征根 $x_j$ 的重数为 $t_j(1\leq j\leq s)$,则数列 $\set{a_n}$ 的通项公式为
$$a_n=A_1(n)(x_1)^n+A_2(n)(x_2)^n+\dots+A_s(n)(x_s)^n$$
其中 $A_j=b_j^{t_j-1}+\dots+b_j^1n+b_j^0(1\leq j\leq s)$,这里 $b_j^m(0\leq m\leq t_j-1)$ 都是常数,它们由数列初始值可以确定。
$(1)$ 若数列 $\set{a_n}$ 满足 $a_{n+3}=-3a_{n+2}+4a_n$,且 $a_1=1,a_2=8,a_3=-18$,求数列 $\set{a_n}$ 的通项公式。
$(2)$ 若数列 $\set{a_n}$ 满足对于所有非负整数 $m,n(m\geq n)$,
$$a_{m+n}+a_{m-n}-m+n-1=\frac{1}{2}(a_{2m}+a_{2n})$$
都成立,且 $a_1=3$,求数列 $\set{a_n}$ 的通项公式。
$(3)$ 设边长为 $1$ 的正六边形 $ABCDEF$,$O$ 是六边形的中心,除了六边形的每一条边,我们还从 $O$ 到每个顶点连一条线段,共得到 $12$ 条长度为 $1$ 的线段,一条路径是指动点沿着上述线段( 全部或部分 )移动,始点终点均为点 $O$ 的一条路线。求长度为 $2024$ 的路线共有多少条 ?
注:根的重数就是方程中同样根的数量。
解答:
$(1)$ 特征方程 $x^3=-3x^2+4$,解得根为 $-2$( 重数为 $2$ )和 $1$( 重数为 $1$ )。
设 $a_n=(An+B)\cdot(-2)^n+C\cdot 1^n$,联立 $a_1,a_2,a_3$ 得 $\displaystyle a_n=\left(n-\frac{1}{2}\right)\cdot(-2)^n+2$.
$(2)$ 令 $m=n=0$ 得 $a_0=1$;令 $n=0$ 得 $a_{2m}=4a_m-2m-3(m\geq 0)$
令 $m=1,n=0$ 得 $a_2=7$;令 $m\geq 1,n=1$ 得 $a_{2m}=2a_{m+1}+2a_{m-1}-2m-7$.
联立得 $a_{m+2}-2a_{m+1}+a_m-2=0$。因此 $a_{m+2}-3a_{m+1}+3a_m-a_{m=1}=0$.
特征方程 $x^3-3x^2+3x-1=0$,解得根为 $1$( 重数为 $3$ )。
设 $a_n=(An^2+Bn+C)\cdot 1^n$,联立 $a_0,a_1,a_2$ 得 $a_n=n^2+n+1$.
$(3)$ 设 $a_n$ 表示由 $O$ 到 $O$ 长度为 $n$ 的路径数,$b_n$ 表示从 $A$ 到 $O$ 长度为 $n$ 的路径数。
$$\begin{cases}a_n=6b_{n-1}\\b_n=a_{n-1}+2b_{n-1}\end{cases}\implies a_{n+1}-2a_n-6a_{n-1}=0$$
特征方程 $x^2-2x-6=0$,解得 $x=1\pm\sqrt 7$( 重数均为 $1$ )。
设 $a_n=A(1+\sqrt{7})^n+B(1-\sqrt{7})^n$,联立 $a_1=0,a_2=6$ 得
$$a_n=\frac{1}{14}[(7-\sqrt{7})(1+\sqrt{7})^n+(7+\sqrt{7})(1-\sqrt{7})^n]$$
代入 $n=2024$ 即得答案。
## 不动点法求通项
例 1:$\displaystyle a_1=3,a_n=\frac{4a_{n-1}-2}{a_{n-1}+1}$
$\set{a_n}$ 的特征函数为 $\displaystyle f(x)=\frac{4x-2}{x+1}$,则特征方程为 $\displaystyle\frac{4x-2}{x+1}=x\implies x_1=1,x_2=2$
$$\begin{cases}a_n-1=\displaystyle\frac{4a_{n-1}-2}{a_{n-1}+1}-1=\frac{3(a_{n-1}-1)}{a_{n-1}+1}①\\a_n-2=\displaystyle\frac{4a_{n-1}-2}{a_{n-1}+1}-2=\frac{2(a_{n-1}-2)}{a_{n-1}+1}②\end{cases}\xRightarrow{①\div②}\frac{a_n-1}{a_n-2}=\frac{3}{2}\frac{a_{n-1}-1}{a_{n-1}-2}$$
因此 $\displaystyle\frac{a_n-1}{a_n-2}=\frac{a_1-1}{a_2-2}\left(\frac{3}{2}\right)^{n-1}\implies a_n=\frac{2^{n-2}-2\cdot 3^{n-1}}{2^{n-2}-3^{n-1}}$
例 2:$\displaystyle a_1=5,a_{n+1}=\frac{3a_n-4}{a_n-1}$
$$x=\frac{3x-4}{x-1}\implies x_1=x_2=2\ \ \ \ a_{n+1}-2=\frac{3a_n-4}{a_n-1}-2=\frac{a_n-2}{a_n-1}$$
$$\frac{1}{a_{n+1}-2}=\frac{a_n-1}{a_n-2}=\frac{1}{a_n-2}+1\implies a_n=\frac{3}{3n-2}+2$$
## 三角代换
$\displaystyle a_1=1,a_{n+1}=\frac{a_n}{1+\sqrt{1+a_n^2}}$,求 $\displaystyle\lim_{n\to+\infty}2^na_n$
$$a_n=\tan\theta_n\implies a_{n+1}=\frac{\tan\theta_n}{1+\sqrt{1+\tan^2\theta_n} }=\frac{\tan\theta_n}{1+\sec\theta_n}=\frac{\sin\theta_n}{1+\cos\theta_n}=\tan\frac{\theta_n}{2}$$
$$a_n=\tan\frac{\theta_1}{2^{n-1}}=\tan\frac{\pi}{2^{n+1}}\ \ \ \ \ \ n\to+\infty\implies \tan\frac{\pi}{2^{n+1}}\to \frac{\pi}{2^{n+1}}\ \ \ \ \ \lim_{n\to+\infty}2^na_n=\frac{\pi}{2}$$
## 通项杯——求数列通项公式
来自 [here](https://zhuanlan.zhihu.com/p/408546712) & [here](https://zhuanlan.zhihu.com/p/407534999),我们从第 $3$ 题开始。
3. $\displaystyle \boxed{a_1=\frac{1}{2},a_{n+1}=2a_n^2+2a_n}$
令 $b_n=2a_n+1$ 代入得 $\displaystyle\frac{b_{n+1}-1}{2}=\frac{b_n^2-2b_n+1}{2}+b_n-1$ 即 $\displaystyle b_{n+1}=b_n^2=b_1^{2^{n-1}}=2^{2^{n-1}}$,从而 $\displaystyle a_n=\frac{1}{2}(2^{2^{n-1}}-1)$
4. $\displaystyle \boxed{a_1=\frac{1}{3},a_{n+1}=2a_n^2-1}$
显然当 $a_n\in[-1,1]$ 时 $a_{n+1}\in[-1,1]$,故令 $a_n=\cos x_n,x_n\in[0,\pi]$. 可得 $$x_n=2x_{n-1}=2^{n-1}\arccos\frac{1}{3},a_n=\cos\left(2^{n-1}\arccos\frac{1}{3}\right)$$
5. $\displaystyle \boxed{a_1=1,a_{n+1}=\frac{1}{a_n+1}}$
$$x=\frac{1}{x+1}\implies x_1=\frac{1}{2}(-1+\sqrt{5}),x_2=\frac{1}{2}(-1-\sqrt{5})$$
$$\frac{a_{n+1}-x_1}{a_{n+1}-x_2}=\frac{x_1}{x_2}\frac{a_n-x_1}{a_n-x_2}=\dots=\left(\frac{x_1}{x_2}\right)^n\frac{1-x_1}{1-x_2}=\left(\frac{x_1}{x_2}\right)^{n+2}$$
$$\frac{a_n-x_1}{a_n-x_2}=\left[\frac{1}{2}(-3+\sqrt{5})\right]^{n+1}\implies a_n=\frac{(-1+\sqrt{5})(-1+(\frac{1}{2}(-3+\sqrt{5}))^n)}{-2+2^{-n}(-3+\sqrt{5})^{1+n}}$$
6. $\displaystyle \boxed{a_1=3,a_{n+1}=\sqrt{a_n+2}}$
有 $\displaystyle\frac{a_{n+1}}{2}=\sqrt{\frac{\frac{a_n}{2}+1}{2}}$,因 $\displaystyle\cosh x=\sqrt{\frac{\cosh 2x+1}{2}}$,所以设 $\displaystyle a_{n}=\cosh \theta_n,\theta_{n+1}=\frac{\theta_n}{2}$,得
$$\theta_n=\frac{1}{2^{n-1}}\theta_1=\frac{\cosh^{-1}\frac{3}{2}}{2^{n-1}}, a_n=2\cosh\left(\frac{\cosh^{-1}\frac{3}{2}}{2^{n-1}}\right)$$
7. $\displaystyle \red{\boxed{a_1=1,a_{n+1}=a_n+\sqrt{a_n^2+a_n+1}}}$
令 $a_n$ 为 $b_n$ 的求和,则 $b_{n+1}=\sqrt{a_n^2+a_n+1},b_0=1,b_1=\sqrt{3}$,由几何意义 - **余弦定理**
$$b_{n+1}^2=a_n^2+a_n+1=a_n^2+1-2a_n\cos\frac{2\pi}{3}\implies b_n=\frac{\sqrt{3}}{2\sin(\frac{\pi}{3\cdot 2^n})}$$
$$a_n=\sum_{k=1}^n b_n+a_1=\frac{1}{2}\left[\sqrt{3}\cot\left(\frac{\pi}{3\cdot 2^{n+1}}\right)-1\right]$$
8. $\displaystyle \red{\boxed{a_1=2,2a_{n+1}=a_n+\frac{1}{a_n}}}$
$$a_{n+1}=\frac{a_n^2+1}{2a_n}\implies a_{n+1}+1=\frac{(a_n+1)^2}{2a_n}\implies1-\frac{2}{a_{n+1}+1}=1-\frac{4a_n}{(a_n+1)^2}$$
$$\implies\frac{a_{n+1}-1}{a_{n+1}+1}=\left(\frac{a_n-1}{a_n+1}\right)^2=\left(\frac{a_1-1}{a_1+1}\right)^{2^n}=\frac{1}{3^{2^n}}\implies a_n=\frac{3^{2^{n-1}}+1}{3^{2^{n-1}}-1}$$
9. $\displaystyle \boxed{a_1=1,a_{n+1}=a_n^3+3a_n}$
$$\frac{a_{n+1}}{2}=4\left(\frac{a_n}{2}\right)^3+3\left(\frac{a_n}{2}\right)\xrightleftharpoons{\frac{a_n}{2}=\sinh \theta_n}\sinh \theta_{n+1}=4\sinh^3\theta_n+3\sinh\theta_n$$
$$\implies\theta_{n+1}=3\theta_n=3^{n-1}\theta_1=3^{n-1}\sinh^{-1}\frac{1}{2}\implies a_n=2\sinh \left(3^{n-1}\sinh^{-1}\frac{1}{2}\right)$$
## 数学归纳法
这部分内容为人教版选学内容,但是学习数归十分有必要。同学们使用时需注意数归是个**容错度低**的方法,只要有错大题分全扣,全对才给分。
一般地,证明一个与正整数 $n$ 有关的命题,可按下列步骤进行:
1. ( 归纳奠基 )证明当 $n=n_0$ 时命题成立。
2. ( 归纳递推 )以“当 $n=k(k\in\N^+,k\geq n_0)$ 时命题成立”为条件推出 “当 $n=k+1$ 时命题也成立”。
完成以上 $2$ 个步骤就可以证明命题对从 $n_0$ 开始的所有正整数 $n$ 都成立。
例 1:证明 $\displaystyle\sum_{i=1}^n i^2=\frac{1}{6}n(n+1)(2n+1)$
(1)当 $n=1$ 时,$\displaystyle 1^2=1=\frac{1}{6}\cdot 1\cdot 2\cdot 3$,命题成立。
(2)假设当 $n=k$ 时,命题成立,那么当 $n=k+1$ 时有:
$$\displaystyle\sum_{i=1}^{k+1} i^2=\frac{1}{6}k(k+1)(2k+1)+(k+1)^2=\frac{(k+1)(k+2)(2k+3)}{6}$$
即当 $n=k+1$ 时,命题也成立。
由 (1)(2) 可知,命题对任意 $n\in\N^+$ 都成立。
练:证明 $\displaystyle\sum_{i=1}^n i\times (i+1)^2=\frac{1}{12}n(n+1)(3n^2+11n+10)$.
例 2:( 2012 湖北卷 )
$(1)$ 已知函数 $f(x)=rx-x^r+(1-r)(x>0,0<r<1)$ 且 $r$ 为有理数,求 $f(x)_{\min}$.
$(2)$ 用 $(1)$ 的结果证明:设 $a_1,a_2\geq 0,b_1,b_2$ 为正有理数,若 $b_1+b_2=1$,则 $a_1^{b_1}a_2^{b_2}\leq a_1b_1+a_2b_2$。
$(3)$ 将 $(2)$ 中的命题推广到一般形式并用数学归纳法证明。
解:$(1)$ 求导得 $f'(x)=0\implies x=1,f(x)_{\min}=f(1)=0$.
$(2)$ 由 $(1)$ 得当 $x\in(0,+\infty)$ 时,$f(x)\geq f(1)=0$,即 $x^r\leq rx+(1-r)$.
若 $r_1r_2=0$,则原命题成立。
若 $r_1r_2\neq 0$,则 $b_2=1-b_1$,令 $\displaystyle x=\frac{a_1}{a_2},r=b_1$,得 $$\left(\frac{a_1}{a_2}\right)^{b_1}\leq b_1\cdot \frac{a_1}{a_2}+(1-b_1)\implies a_1^{b_1}a_2^{1-b_1}\leq a_1b_1+a_2(1-b_1)$$
原命题成立。
$(3)$ 推广:$\displaystyle\sum_{i=1}^n b_i=1\implies \prod_{i=1}^n a_i^{b_i}\leq \sum_{i=1}^n a_ib_i$
① 当 $n=1$ 时推广成立。
② 假设 $n=k$ 时成立,且 $\displaystyle\sum_{i=1}^k b_i=1$,则 $\displaystyle\prod_{i=1}^k a_i^{b_i}\leq \sum_{i=1}^k a_ib_i$.
当 $n=k+1$ 时,$\displaystyle\sum_{i=1}^{k+1} b_i=1$,于是 $a_1^{b_1}a_2^{b_2}\dots a_k^{b_k}a_{k+1}^{b_{k+1}}=\left(a_1^{\frac{b_1}{1-b_{k+1}}}a_2^{\frac{b_2}{1-b_{k+1}}}\dots a_k^{\frac{b_k}{1-b_{k+1}}}\right)a_{k+1}^{b_{k+1}}$
因 $\displaystyle\sum_{i=1}^n \frac{b_i}{1-b_{k+1}}=1$,由归纳假设得 $\displaystyle\left(a_1^{\frac{b_1}{1-b_{k+1}}}a_2^{\frac{b_2}{1-b_{k+1}}}\dots a_k^{\frac{b_k}{1-b_{k+1}}}\right)\leq\frac{a_1b_1+a_2b_2+\dots a_kb_k}{1-b_{k+1}}$
又因 $(1-b_{k+1})+b_{k+1}=1$,得 $$\displaystyle\left(\frac{a_1b_1+a_2b_2+\dots a_kb_k}{1-b_{k+1}}\right)^{1-b_{k+1}}a_{k+1}^{b_{k+1}}\leq\frac{a_1b_1+a_2b_2+\dots+a_kb_k}{1-b_{k+1}}\cdot(1-b_{k+1})+a_{k+1}b_{k+1}$$
从而当 $n=k+1$ 时,推广成立。
结合 ①②,对于一切正整数 $n$,推广命题成立。
## 放缩
#### 分式型
已知正项数列满足 $4a_{n+1}^2a_n-5a_n^2a_{n+1}+4a_n-5a_{n+1}=0,a_1=2$.
$(1)$ 设 $\displaystyle b_n=a_n+\frac{1}{a_n}$,求证:$\set{b_n}$ 是等比数列。
$(2)$ 设 $\displaystyle c_n=\frac{b_n}{b_n^2-4}$,求证:$c_1+c_2+\dots+c_n<\displaystyle\frac{50}{9}$.
$(3)$ 设 $\displaystyle A_n=a_1^2+a_2^2+\dots+a_n^2,B_n=\frac{1}{a_1^2}+\frac{1}{a_2^2}+\dots+\frac{1}{a_n^2}$,是否存在 $n$ 使得 $32^{n-1}(A_n+B_n)$ 为整数 ? 若是,求出 $n$ 应满足的条件;若不存在,说明理由。
解析:$(1)\ \displaystyle b_n=2\cdot\left(\frac{5}{4}\right)^n,b_1=\frac{5}{2},b_2=\frac{25}{8},c_1=\frac{10}{9},c_2=\frac{200}{369}$.
$(2)\displaystyle \ c_n=\frac{1}{2}\frac{\left(\frac{5}{4}\right)^n}{\left(\frac{5}{4}\right)^{2n}-1}=\frac{1}{2}\frac{\left(\frac{4}{5}\right)^{-n}}{\left(\frac{4}{5}\right)^{-2n}-1}=\frac{1}{2}\frac{\left(\frac{4}{5}\right)^n}{1-\left(\frac{4}{5}\right)^{2n}}\leq\frac{1}{2}\frac{\left(\frac{4}{5}\right)^n}{1-\left(\frac{4}{5}\right)^2}=\frac{25}{18}\cdot\left(\frac{4}{5}\right)^n$.
另外一种放缩:$\displaystyle c_n=\frac{1}{b_n-\frac{4}{b_n}}=\frac{1}{2}\frac{1}{(\frac{5}{4})^n-(\frac{4}{5})^n}=\frac{1}{2}(\frac{4}{5})^n\frac{1}{1-(\frac{16}{25})^n}\leq\frac{1}{2}\left(\frac{4}{5}\right)^n\frac{1}{1-\frac{16}{25}}=\frac{25}{18}\cdot\left(\frac{4}{5}\right)^n$.
关键要想到当等比 $|q|<1$ 时 $S_n$ 会收敛的特性。 $\displaystyle\sum_{n=1}^{\infty}c_n<\frac{25}{18}\frac{\frac{4}{5}}{1-\frac{4}{5}}=\frac{50}{9}$.
$(3)\displaystyle\ A_n+B_n=\sum_{k=1}^{n}b_k^2+2n=4\sum_{k=1}^n\left(\frac{25}{16}\right)^n+2n$ 只要 $32^{n-1}=2^{5n-5}$ 能与 $\displaystyle 4\times\left(\frac{1}{16}\right)^n=2^{2-4n}$ 抵消即可,即 $5n-5\geq 4n-2$,答案为 $n\geq 3$.
#### 根号型
$$\red{\boxed{2(\sqrt{n+1}-\sqrt{n})}=\frac{2}{\sqrt{n}+\sqrt{n+1}}<\boxed{\frac{1}{\sqrt{n}}=\frac{2}{\sqrt{n}+\sqrt{n}}}<\frac{2}{\sqrt{n}+\sqrt{n-1}}=\boxed{2(\sqrt{n}-\sqrt{n-1})}}$$
例 1( 一个较大的放缩 ):$\displaystyle\begin{aligned}\sum_{k=1}^n\frac{1}{\sqrt{3k+2}}&=\frac{1}{\sqrt{5}}+\frac{1}{\sqrt{8}}+\frac{1}{\sqrt{11}}+\dots+\frac{1}{\sqrt{3n+2}}<\frac{2}{3}\sqrt{3n+2}\\&<\frac{2}{3}(\sqrt{5}-\sqrt{2}+\sqrt{8}-\sqrt{5}+\sqrt{11}-\sqrt{8}+\dots+\sqrt{3n+2}-\sqrt{3n-1})\\&=\frac{2}{3}(\sqrt{3n+2}-\sqrt{2})\end{aligned}$
例 2:$\displaystyle a_1=1,a_{n+1}=a_n+4\left(\sqrt{a_n}+\frac{1}{\sqrt{a_n}}\right)$,记 $\displaystyle\set{\frac{1}{a_n}}$ 的前缀和为 $S_n$,则 $S_{2022}$ 的范围 ?
$\displaystyle\text{A.}\ \left(\frac{7}{3},\frac{8}{3}\right)\ \ \ \ \text{B.}\ \left(2,\frac{7}{3}\right)\ \ \ \ \text{C.}\ \left(\frac{5}{3},2\right)\ \ \ \ \text{D.}\ \left(1,\frac{5}{3}\right)$
$$a_{n+1}\geq a_n+4\sqrt{a_n}>a_n+2\sqrt{a_n}+1\implies a_n\geq n^2,S_n\leq\frac{\pi^2}{6}<\frac{5}{3}$$
$$\begin{aligned}\frac{1}{n^2}&<\frac{1}{n^2-1}=\frac{1}{2}\left(\frac{1}{n-1}-\frac{1}{n+1}\right)\\ &<\frac{1}{n^2-\frac{1}{4}}=2\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right) \end{aligned}$$
可用于证 $\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}<\frac{5}{3}$ 或 $\displaystyle\frac{7}{4}$.
#### 三角型
设数列 $\set{x_n}$ 满足:$x_1=1,x_n>0$ 且 $\displaystyle x_{n+1}=\frac{\sqrt{x_n^2+1}-1}{x_n}$,设 $\tan a_n=x_n$,记 $\set{x_n}$ 的前缀和为 $S_n$,求 $a_n$ 通项并证明 $S_n<2$.
首先 $x_n$ 单调递减,$\displaystyle a_1=\frac{\pi}{4}$. 题目给的条件可以化简为 $x_n(x_nx_{n+1}^2+2x_{n+1}-x_n)=0$ 于是 $\displaystyle x_n=\frac{2x_{n+1}}{1-x_{n+1}^2}$,代入 $\tan a_n=x_n$ 得 $\displaystyle\tan(a_n)=\tan(2a_{n+1}),a_n=2a_{n+1}=\frac{\pi}{2^{n+1}}$
可知 $\displaystyle x_n=\tan\left(\frac{\pi}{2^{n+1}}\right)$,而 $\displaystyle\tan x\leq\frac{4}{\pi}x\left(0<x\leq\frac{\pi}{4}\right)$( 读者自证 ),由此
$$S_n=\tan\frac{\pi}{4}+\tan\frac{\pi}{8}+\dots<1+\frac{1}{2}+\dots=2$$
# 导数
## 基本初等函数的导数公式
| $f(x)$ | $c$ | $x^a$ | $a^x$ | $\log_a x$ | $\sin x$ | $\cos x$ | $\arcsin x$ | $\arccos x$ | $\arctan x$ |
| :-----: | :---: | :--------: | :--------: | :----------------: | :------: | :-------: |:-:|:-:|:-:|
| $f'(x)$ | $0$ | $ax^{a-1}$ | $a^x\ln a$ | $\displaystyle\frac{1}{x\ln a}$ | $\cos x$ | $-\sin x$ | $\displaystyle\frac{1}{\sqrt{1-x^2} }$ | $\displaystyle -\frac{1}{\sqrt{1-x^2} }$ | $\displaystyle\frac{1}{1+x^2}$ |
## 运算法则
- $[f(x)\pm g(x)]'=f'(x)\pm g'(x)$
- $[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)$
- $\displaystyle\left[\frac{f(x)}{g(x)}\right]'=\frac{g(x)f'(x)-f(x)g'(x)}{g^2(x)}\ \ \ (g(x)\neq 0)$
- $[cf(x)]'=cf'(x)$
- $[af(x)\pm bg(x)]'=af'(x)\pm bg'(x)$
- $\displaystyle\left[\frac{1}{g(x)}\right]'=-\frac{g'(x)}{g^2(x)}\ \ \ (g(x)\neq 0)$
- 复合函数 $y=f(g(x))$ 的导数,与 $y=f(u), u=g(x)$ 的关系:$y_x^{'}=y_u^{'}\cdot u_x^{'}$
即 $y$ 对 $x$ 的导数等于 $y$ 对 $u$ 的导数乘 $u$ 对 $x$ 的导数。
例 1:求 $f(x)=(3x+5)^3$ 的导数 $f'(x)$,可以看作 $y=u^3$ 与 $u=3x+5$ 的复合函数。
$y_x^{'}=y_u^{'}\cdot u_x^{'}=(u^3)'\cdot (3x+5)'=3u^2 \times 3 = 9(3x+5)^2$
例 2:求 $f(x)=e^{-0.05x+1}$ 的导数 $f'(x)=(e^{u})'\cdot(-0.05x+1)'=-0.05e^{-0.05x+1}$
例 3:求 $f(x)=\ln(2x-1)$ 的导数 $\displaystyle f'(x)=(\ln{u})'\cdot(2x-1)'=\frac{1}{u}\times 2=\frac{2}{2x-1}$
- $f(x)$ 在 $x=x_0$ 处取极值时,$f'(x_0)=0$.
- $f(x)$ 在 $x=x_0$ 处的切线斜率 $k=f'(x_0)$,切线方程 $y=f'(x_0)(x-x_0)+f(x_0)$.
- 多个函数乘积的求导法则:$(uvw)'=u'vw+uv'w+uvw'$
### 重要不等式
$$\sin x<x<\tan x\ \ \ \ \ \ \ \left(x\in\left(0,\frac{\pi}{2}\right)\right)$$
$$1+x\leq e^x\leq\frac{1}{1-x}\ \ \ \ \ \ \ \ \ \ x<1$$
$$\frac{x-1}{x}\leq \ln x\leq x-1\ \ \ \ \ \ \ \ \ \ x>0$$
$$\frac{x-1}{x}\leq\frac{2(x-1)}{x+1}\leq\ln x\leq\frac{1}{2}(x-\frac{1}{x})\leq x-1\ \ \ \ \ \ \ \ \ \ x\geq 1$$
$$\sqrt{ab}<\frac{a-b}{\ln a-\ln b}<\frac{a+b}{2}\ \ \ \ \ \ \ \ \ \ a>0,b>0,a\neq b$$
一些例题:
1. 已知 $f(x)=\cos x+\ln(x+1)$.
$(1)$ 若 $f(x)\leq ax+1$ 恒成立,求 $a$ 的值。
$(2)$ 证明:$\displaystyle\sum_{k=n+1}^{2n}f(\sin\frac{1}{k}-1)<\ln 2,n\in\N^*$.
解:$(1) a=1$,得到 $f(x)=\cos x+\ln(x+1)\leq x+1$.
$(2)\ \displaystyle\sum_{k=n+1}^{2n}f\left(\sin\frac{1}{k}-1\right)\leq\sum_{k=n+1}^{2n}\sin\frac{1}{k}<\sum_{k=n+1}^{2n}\frac{1}{k}$
由 $e^x\geq x+1$ 得到 $\ln x<x-1$,令 $\displaystyle x=\frac{n}{n+1}$ 得到 $\displaystyle\frac{1}{n+1}<\ln\frac{n+1}{n}$,于是
$$\sum_{k=n+1}^{2n}\frac{1}{k}<\sum_{k=n+1}^{2n}\ln\frac{k+1}{k}=\ln(2n)-\ln n=\ln 2$$
---
2. 设 $f(x)=\ln(1+x),g(x)=xf'(x),x\geq 0$.
$(1)$ 若 $f(x)\geq ag(x)$ 恒成立,求 $a$ 范围。
$(2)$ 设 $n\in\N^*$,比较 $g(1)+g(2)+\dots+g(n)$ 与 $n-f(n)$ 的大小,并加以证明。
解:$(1)\ a\in(-\infty,1]$.
$$(2)\ g(1)+g(2)+\dots+g(n)=\frac{1}{2}+\frac{2}{3}+\dots+\frac{n}{n+1}=n-\frac{1}{2}-\frac{1}{3}-\dots-\frac{1}{n+1}$$
只用证 $\displaystyle \frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n+1}<\ln(n+1)=\ln\frac{n+1}{n}+\ln\frac{n}{n-1}+\dots+\ln\frac{2}{1}$
只用证 $\displaystyle\red{\boxed{\frac{1}{n+1}<\ln\frac{n+1}{n}}}$( 这是个很重要的不等式,会经常用到!)由 $(1)$ 即证。
也可以这样:由 $\ln (x+1)<x$,代入 $\displaystyle x=-\frac{1}{n+1}$ 即证。
---
3. 证明:$\displaystyle\sum_{k=1}^n\sqrt{\frac{k+1}{k}}-\sum_{k=1}^n\sqrt{\frac{k}{k+1}}>\ln(n+1)$,$n\in\N^*$.
只用证 $\displaystyle\sqrt{\frac{n+1}{n}}-\sqrt{\frac{n}{n+1}}>\ln\frac{n+1}{n}$,也就是 $\displaystyle\red{\boxed{\frac{1}{\sqrt{n^2+n}}>\ln\frac{n+1}{n}}}$
我们设 $u=\displaystyle\frac{n+1}{n}$ 换元,只用证 $\sqrt{u}-\displaystyle\frac{1}{\sqrt{u}}>\ln u$,求导很容易证。
---
4. 已知 $\displaystyle f(x)=x^2-e^{\lambda x-\frac{1}{x}}$. $(1)\ x\geq 1$ 时 $f(x)\leq 0$,求 $\lambda$ 范围。$(2)$ 求证:$\displaystyle e^{\frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{4n}}>2e^{-\frac{1}{4n}}$.
$(1)\ \lambda\in[1,+\infty)\ \ \ \ \ \ \ \ \ \ \ \ \ (2)$ 即证 $\displaystyle\frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n}>\ln 2-\frac{1}{4n}$
由 $(1)$ 得 $\displaystyle e^{x-\frac{1}{x}}\geq x^2\implies\ln x\leq \frac{1}{2}\left(x-\frac{1}{x}\right)\implies \ln\frac{n+1}{n}\leq\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)$
$$\begin{aligned}\ln 2&=\ln\frac{n+1}{n}+\ln\frac{n+2}{n+1}+\dots+\ln\frac{2n}{2n-1}\\&<\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n-1}+\frac{1}{2n}\right)\\&=\frac{1}{2n}+\frac{1}{n+1}+\frac{1}{n+2}+\dots+\frac{1}{2n-1}+\frac{1}{4n}\end{aligned}$$
原题得证。此外,笔者在初次做这道题时,是通过构造函数 $\displaystyle \frac{1}{n+1}>\ln\frac{n+1}{n}-\frac{1}{2n(n+1)}$ 做的,十分麻烦并且花费了大约 $1$ 个小时的时间,还是利用 $(1)$ 的结论最好。并且提醒:此题不能直接数学归纳法。
### 三次函数
设 $f(x)=ax^3+bx^2+cx+d$,则 $f'(x)=3ax^2+2bx+c$. 对于方程 $f'(x)=0$,我们记它的根的判别式 $\Delta=4b^2-12ac$. 当 $\Delta >0$ 时,记 $x_1,x_2$ 为方程的根,即 $f(x)$ 的极值点。
1. $f(x)=0$ 有 $1$ 个根 $\xleftrightarrow{}\Delta\leq 0$ 或 $\begin{cases}\Delta>0 \\ f(x_1)f(x_2)>0\end{cases}$
2. $f(x)=0$ 有 $2$ 个根 $\xleftrightarrow{}\begin{cases}\Delta>0 \\ f(x_1)f(x_2)=0\end{cases}$
3. $f(x)=0$ 有 $3$ 个根 $\xleftrightarrow{}\begin{cases}\Delta>0 \\ f(x_1)f(x_2)<0\end{cases}$
练习题:
$(1)$ 若 $\displaystyle f(x)=\frac{1}{3}x^3+\frac{1}{2}ax^2+1$ 有一个零点,求实数 $a$ 的取值范围。
$(2)$ 若 $\displaystyle f(x)=\frac{1}{3}x^3+ax+1$ 有两个零点,求实数 $a$ 的取值范围。
$(3)$ 若 $f(x)=x^3-3a^2x+2(a>0)$ 有三个零点,求实数 $a$ 的取值范围。
答案分别为 $\displaystyle \left(-\sqrt[3]{6},+\infty\right),\set{-\sqrt[3]{\frac{9}{4}}},(1,+\infty)$
【2014 北京文 T20】$f(x)=2x^3-3x$.
$(1)$ 若过 $P(1,m)$ 存在 $3$ 条直线与曲线 $y=f(x)$ 相切,求 $m$ 的取值范围。
$(2)$ 问过点 $A(-1,2),B(2,10),C(0,2)$ 分别存在多少条直线与曲线 $y=f(x)$ 相切 ?直接写出答案。
$f'(x)=6x^2-3$,设切点 $(t,f(t))$,则切线方程 $y-(2t^2-3t)=(6t^2-3)(x-t)$. 设切线过 $(a,b)$,则 $4t^3-6at^2+3a+b=0$,令 $g(t)=4t^3-6at^2+3a+b,g'(t)=12t^2-12at=0\implies t_1=0,t_2=a$.
$(1)$ $(a,b)=(1,m),g(t)_{\max}=g(0)=m+3>0,g(t)_{\min}=g(1)=m+1<0\implies m\in(-3,-1)$.
$(2)$ 答案分别为 $3,2,1$.
#### 整体代换
【2018 II 卷文 T21】证明 $\displaystyle f(x)=\frac{1}{3}x^3-a(x^2+x+1)$ 只有 $1$ 个零点。
$f'(x)=x^2-2ax-a,\Delta=4a^2+4a$
$(1)$ 当 $-1\leq a\leq 0$ 时,$f'(x)\geq 0$ 恒成立,故 $f(x)$ 在 $\R$ 上 $\uparrow$,只有 $1$ 个零点。
$(2)$ 当 $a>0$ 或 $a<-1$ 时,$f'(x)=0$ 有两个根 $x_1,x_2$,由题意 $f(x_1)f(x_2)>0$. 由 $f'(x_1)=x_1^2-2ax_1-a=0$ 得 $x_1^2=2ax_1+a$,则
$$\begin{aligned}f(x_1)&=\frac{1}{3}x_1^3-a(x_1^2+x_1+1)=\frac{1}{3}x_1(2ax_1+a)-a(x_1^2+x_1+a)\\&=-\frac{a}{3}x_1^2-\frac{2a}{3}x_1-a=-\frac{2}{3}a(a+1)x_1-\left(\frac{a^2}{3}+a\right)\end{aligned}$$
同理 $\displaystyle f(x_2)=-\frac{2}{3}a(a+1)x_2-\left(\frac{a^2}{3}+a\right)$,由韦达定理 $x_1+x_2=2a,x_1x_2=-a$,得到 $\displaystyle f(x_1)f(x_2)=\frac{1}{9}a^2\left[\left(3a+\frac{7}{3}\right)^2+\frac{32}{9}\right]>0$
#### 对称中心
- 已知 $f(x)=ax^3+bx^2+cx+d$,则 $f(x)$ 的对称中心为 $\displaystyle\red{\boxed{\left(-\frac{b}{3a},f\left(-\frac{b}{3a}\right)\right)}}$,此时 $f''(x)=0$. 若 $x_1,x_2$ 是 $f(x)$ 的极值点或 $x_1,x_2$ 关于 $\displaystyle x=-\frac{b}{3a}$ 对称,则 $\displaystyle \frac{f(x_1)+f(x_2)}{2}=f\left(\frac{x_1+x_2}{2}\right)=f\left(-\frac{b}{3a}\right)$.
why 对称中心为 $\displaystyle\left(-\frac{b}{3a},f\left(-\frac{b}{3a}\right)\right)$:对任意 $x$,存在 $\displaystyle f(x)+f\left(-\frac{2b}{3a}-x\right)=2\left(-\frac{b}{3a}\right)$.
【2012 大纲卷文 T21】设 $\displaystyle f(x)=\frac{1}{3}x^3+x^2+ax$ 有两个极值点 $(x_1,x_2)$,若过两点 $(x_1,f(x_1)),(x_2,f(x_2))$ 的直线 $l$ 与 $x$ 轴的交点在曲线 $y=f(x)$ 上,求 $a$ 的值。
$f'(x)=x^2+2x+a=0$ 有两根 $x_1,x_2$,由 $\Delta=4-4a>0\implies a<1$.
由韦达定理 $\begin{cases}x_1+x_2=-2\\x_1x_2=a\end{cases}$,斜率 $\displaystyle k=\frac{f(x_2)-f(x_1)}{x_2-x_1}=\frac{2}{3}(a-1)$。
直线 $l$ 必过中点 $\displaystyle \left(-1,\frac{2}{3}-a\right)$. 所以直线方程 $\displaystyle y-\left(\frac{2}{3}-a\right)=\frac{2}{3}(a-1)(x+1)$,令 $y=0$ 得 $\displaystyle x=\frac{a}{2(a-1)}$,代入 $f(x)$ 得 $a=0$ 或 $\displaystyle\frac{2}{3}$ 或 $\displaystyle\frac{3}{4}$.
## 复合函数方程有解问题
这部分高一上学期应该有所涉及,方法是画出图像然后分析。先来两道入门题。
1. 已知 $f(x)=|x^2-4x|$,求方程 $f^2(x)-3f(x)+2=0$ 的实数根的个数。
2. 已知 $f(x)=|x^2-4x|$,求方程 $f^2(x)-3af(x)+2a^2=0$ 的实数根的个数。
答案:
1. $f^2(x)-3f(x)+2=[f(x)-1][f(x)-2]=0\implies x=1\ \text{or}\ 2$,画图得共 $8$ 个实数根。
2. $f^2(x)-3af(x)+2a^2=[f(x)-a][f(x)-2a]=0\implies x=a\ \text{or}\ 2a$,接下来分类讨论即可。
这两题都可因式分解,换个难点的:
3. 已知 $f(x)=\begin{cases}
x^2 & x\leq 0 \\
4\sin x & 0< x\leq \pi
\end{cases}$,方程 $f(f(x))=0$ 有多少个解 ?
要让 $f(t)=0$,那么解得 $t=0/\pi$,只要统计满足 $f(x)=t$ 的 $x$ 个数即可。答案是 $5$.
太简单了。上导数。
4. $\displaystyle f(x)=\frac{x}{e^{x-1}}$,若关于 $x$ 的方程 $f^2(x)-m|f(x)|-2m-3=0$ 有三个不同实数根,求 $m$ 范围。
$f'(x)=\frac{1-x}{e^{x-1}}=0\implies x=1,x<1,f(x)\uparrow,x>1,f(x)\downarrow,f(x)_{\max}=f(1)=1$.
显然 $\displaystyle f(0)=0,\lim_{x\to-\infty}f(x)=-\infty,\lim_{x\to+\infty}f(x)=0$,于是可以做出 $t=|f(x)|$ 图像。
原题变为 $g(t)=t^2-mt-2m-3=0(t\geq 0)$,接下来分类讨论:
① 只有一个根 $t_0$,$\begin{cases}\Delta=m^2+8m+12=0\\ \displaystyle 0<t_0=\frac{m}{2}<1\end{cases}$,此时无解。
② 两个根 $t_1,t_2$,$\Delta>0\implies m<-6/m>-2$,继续分类讨论。这时候要根据图像推范围。
$(1)\ t_1<0,0<t_2<1$,即 $g(0)<0,g(1)>0$,解得 $\displaystyle -\frac{3}{2}<m<-\frac{2}{3}$.
$(2)\ t_1=0,t_2=1$,容易验证无解。
$(3)\ t_1=1,t_2>1$,得 $\displaystyle m=-\frac{2}{3}$,$\displaystyle t_2=-\frac{5}{3}$,排除。
所以答案 $\displaystyle\left(-\frac{3}{2},-\frac{2}{3}\right)$.
5. 【2019 GD 二模理 T12】$f(x)=\begin{cases}1-x & x\leq 0 \\ \log_2x & x>0\end{cases}$,若关于 $x$ 的方程 $f(f(x))=m$ 有两个不同根 $x_1,x_2$,求 $x_1+x_2$ 范围。
答案:$[2,3)$. $m$ 的范围是 $[0,1)$.
6. 【2024 HB 八市联考】已知函数 $f(x)=ax^3+bx^2+cx+d$ 存在两个极值点 $x_1,x_2(x_1<x_2)$,且 $f(x_1)=-x_1,f(x_2)=x_2$. 设 $f(x)$ 的零点个数为 $m$,方程 $3af^2(x)+2bf(x)+c=0$ 的实根个数为 $n$,则
$\text{A.}$ 当 $a>0$ 时,$n=3$ $\ \ \ \ \ \text{B.}$ 当 $a<0$ 时,$m+2=n$
$\text{C.}\ nm$ 一定能被 $3$ 整除 $\ \ \ \ \ \ \text{D.}\ m+n$ 的取值集合为 $\set{4,5,6,7}$
答案:$\text{AB}$.
解析:显然 $x_1,x_2$ 是 $f'(x)=3ax^2+2bx+c$ 的零点,而 $f(f'(x))=3af^2(x)+2bf(x)+c=0$,因此 $f(x)=x_1$ 或 $x_2$.
当 $a>0$ 时,$f(x)$ 在 $(-\infty,x_1),(x_2,+\infty)\uparrow,(x_1,x_2)\downarrow,f(x)_{\max}=f(x_1)=-x_1,f(x)_{\min}=f(x_2)=x_2$,显然 $-x_1>x_2$,所以 $x_1<0,x_2>0$,$f(x)=x_1$ 有 $1$ 个根,$f(x)=x_2$ 有 $2$ 个根,$n=3$,故 $\text{A}$ 正确。( 以下建议画图理解 )
1. $f(x_2)=x_2>0,m=1,nm=3,n+m=4$
2. $f(x_2)=x_2=0,m=2,nm=6,n+m=5$
3. $f(x_2)=x_2<0,m=3,nm=9,n+m=6$
当 $a<0$ 时,$f(x)$ 在 $(-\infty,x_1),(x_2,+\infty)\downarrow,(x_1,x_2)\uparrow,f(x)_{\max}=f(x_2)=x_2,f(x)_{\min}=f(x_1)=-x_1$,显然 $x_2>-x_1$,所以 $x_2>0$.
1. $f(x_1)=-x_1>0,x_1<0,m=1,n=3,nm=3,n+m=4$
2. $f(x_1)=-x_1=0,x_1=0,m=2,n=4,nm=8,n+m=6$
3. $f(x_1)=-x_1<0,x_1>0,m=3,n=5,nm=15,n+m=8$
#### $f(f(x))=x$ 或 $f(g(x))=x$ 型
1. 若 $f(x)$ 单调,则 $f(f(x))=x$ 的解与 $f(x)=x$ 的解相同
2. $f(f(x))=x$ 有解 $\iff\ f(x)=x$ 有解。
3. $f(f(x))=x$ 无解 $\iff\ f(x)=x$ 无解。
4. $f(g(x))=x$ 有解 $\iff\ g(f(x))=x$ 有解。
两道练习题:
1. 【2013 SC 理 T10】$f(x)=\sqrt{e^x+x-a}$. 若曲线 $y=\sin x$ 上存在 $(x_0,y_0)$ 使得 $f(f(y_0))=y_0$,求 $a$ 的范围。
答案:$[1,e]$. 问题等价于 $f(x)=x$ 在 $[0,1]$ 上有解,答案即 $a=-x^2+x+e^x$ 在 $[0,1]$ 上的值域。
2. $\displaystyle f(x)=\ln x+\frac{1}{2}x-a$,若存在 $b\in[1,e]$ 使得 $f(f(b))=b$,求 $a$ 的范围。
答案:$\displaystyle\left[-\frac{1}{2},\ln 2-1\right]$。问题等价于 $f(x)=x$ 在 $[1,e]$ 上有解,即 $\displaystyle a=\ln x -\frac{x}{2}$ 在 $[1,e]$ 上的值域。
## 简单的恒成立问题
- $f(x)\geq 0$ 在定义域内恒成立等价于 $f(x)_{\min}\geq 0$.
- $f(x)\leq 0$ 在定义域内恒成立等价于 $f(x)_{\max}\leq 0$.
来一道简单题:【2013 全国理 T9】$f(x)=x^2+ax+\frac{1}{x}$ 在 $(\frac{1}{2},+\infty)$ 是增函数,求 $a$ 的取值范围。
答案:$[3,+\infty)$. 参数分离即可。
当涉及指数函数或对数函数**并且难以直接求导数零点**时,就要考虑以下这种方法。( 新高掌 P112 )
- **指数找队友**:形如 $\boxed{e^xf(x)}$ 或 $\boxed{e^{-x}f(x)}$ 求导后是 $\boxed{e^x[f(x)+f'(x)]}$ 和 $\boxed{-e^{-x}[f(x)-f'(x)]}$,显然 **其导数的零点和指数函数毫无关系!** 因此可以将函数变形成 $e^{\pm x}f(x)$ 的形式再求导数零点。
注意:
1. 不一定需要变形。
2. 若要求 $f(x)$ 的最值、极值、单调性就不能使用这个方法。
【2013 I 理 T21】$f(x)=x^2+4x+2,g(x)=e^x(2x+2)$,若 $x\geq -2$ 时,$f(x)\leq kg(x)$,求 $k$ 取值范围。
分离参数得 $\displaystyle\begin{cases}
\displaystyle k\leq \frac{e^{-x} (x^2+4x+2)}{2x+2} & x\in[-2,-1) \\
\displaystyle k\geq \frac{e^{-x} (x^2+4x+2)}{2x+2} & x\in[-1,+\infty)
\end{cases}$ 令 $h(x)=\frac{e^{-x}(x^2+4x+2)}{2x+2}$,则问题转化为求 $h(x)$ 在 $[-2,-1)$ 上最小值,$(-1,+\infty)$ 上最大值。
由 $\displaystyle h'(x)=\frac{e^{-x}\cdot -2x(x+2)^2}{(2x+2)^2}$ 得 $[-2,-1)\cup(-1,0)$ 上 $h'(x)\geq 0$,$(0,+\infty)$ 上 $h'(x)<0$. 故在 $[-2,-1)$ 上 $h(x)_{\min}=h(-2)=e^2$,$(-1,+\infty)$ 上 $h(x)_{\max}=h(0)=1$. 即 $k\in[1,e^2]$.
- **对数单身狗**:形如 $\boxed{f(x)+\ln g(x)}$ 的函数求导后是 $\boxed{f'(x)+\frac{g'(x)}{g(x)}}$,显然 **其导数的零点和对数函数毫无关系!** 因此可以将函数变形成 $f(x)+\ln g(x)$ 的形式再求导数零点。
也有另外一种形式:$y=f(x)(\ln f(x)+C),y'=f'(x)(\ln f(x)+C+1)$,其中 $C$ 为常数。
已知 $f(x)=x\ln x,g(x)=-x^2+ax-3,\forall x\in(0,+\infty),2f(x)\leq g(x)$ 恒成立,求 $a$ 范围。
原问题等价于 $\displaystyle a\leq 2\ln x+x+\frac{3}{x}$,令 $\displaystyle h(x)=2\ln x+x+\frac{3}{x},h'(x)=\frac{2}{x}+1-\frac{3}{x^2}=\frac{(x+3)(x-1)}{x^2}=0\implies x=1\ \text{or}\ -3$( 舍去 )。所以 $h(x)$ 在 $(0,1]$ 上 $\downarrow$,在 $[1,+\infty)$ 上 $\uparrow$。得到 $a\leq h(x)_{\min}=h(1)=4$。
关于任意与存在:相当于求函数值域问题,分类讨论慢慢分析即可。
## 零点问题
参考《新高中数学:你真的掌握了吗? 函数》难度由 $A\to C$ 依次上升。
### A
- 零点存在定理:若函数 $f(x)$ 在区间 $[a,b]$ 上连续,且 $f(a)f(b)<0$,则 $f(x)$ 在 $[a,b]$ 上必存在零点。注意这一定理不具备必要性。
- 若 $f(x)$ 在 $(a,b)$ 上有零点且单调,则零点唯一。
- 若 $f(x)$ 在 $(a,b)$ 上有唯一零点 $x_0$ 且 $f(a)f(b)>0$,则 $f'(x_0)=0$.
---
1. $\displaystyle 0<a<\frac{4}{\pi}$,若 $f(x)=e^x-\cos x-ax$ 在 $\displaystyle\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ 上有唯一零点,求 $a$.
$f(0)=0\implies f'(0)=0,a=1$.
---
2. 【2012 FJ 文 T22】求 $\displaystyle f(x)=x\sin x-\frac{3}{2}$ 在 $(0,\pi)$ 上的零点个数。
聪明的同学可以直接泰勒展开,但是现在我们要求朴素求导。
显然 $\displaystyle f(0)=f(\pi)=-\frac{3}{2}<0,f'(x)=\sin x+x\cos x$,知 $f'(x)$ 在 $\displaystyle\left(0,\frac{\pi}{2}\right)>0,f'\left(\frac{\pi}{2}\right)>0,f'(\pi)<0$,因此需要继续研究 $f'(x)$ 在 $\displaystyle\left(\frac{\pi}{2},\pi\right)$ 的单调性。
$f''(x)=2\cos x-x\sin x$ 得 $f''(x)$ 在 $\displaystyle\left(\frac{\pi}{2},\pi\right)<0\implies f'(x)\downarrow$,所以 $f'(x)=0$ 在 $\displaystyle\left(\frac{\pi}{2},\pi\right)$ 上有唯一零点 $x_0$,所以 $f(x)$ 在 $(0,x_0) \uparrow,(x_0,\pi)\downarrow$.
即 $\displaystyle f(x)_{\max}=f(x_0)>f\left(\frac{\pi}{2}\right)=\frac{\pi-3}{2}>0$,结合 $\displaystyle f(0)=f(\pi)=-\frac{3}{2}<0$ 得 $f(x)$ 在 $(0,x_0),(x_0,\pi)$ 各有一零点。
练习:求 $\displaystyle f(x)=\frac{1}{2}\sqrt{x}-\cos x$ 在 $(1,\infty)$ 上的零点个数。答案:$1$.
---
3. 已知 $f(x)=e^x-ex-a(x^2-x)$ 在 $(0,1)$ 上有零点,求 $a$ 范围。
$f'(x)=e^x-e-a(2x-1),f''(x)=e^x-2a,f(0)=1,f(1)=0$,所以 $f(x)$ 不单调,$f'(x)$ 有零点。
接下来分 $5$ 类讨论:$\displaystyle a<0,0\leq a\leq\frac{1}{2},\frac{1}{2}<a<\frac{e}{2},\frac{e}{2}\leq a\leq e-1,a>e-1$,对每一类求出 $f'(x)$ 单调性,跟上一题一样判断即可。
答案:$(-\infty,0)$
为什么是这 $5$ 类:来自 $f'(0)=0,f'(1)=0,f''(0)=0,f''(1)=0$,分别求得 $\displaystyle e-1,0,\frac{1}{2},\frac{e}{2}$.
其中前 $2$ 个是由 $f'(x)$ 有零点的临界条件得来,后 $2$ 个由 $f'(x)$ 的单调性得来,即 $f''(x)>0$.
练习:【2014 SC 理 T21】已知 $f(x)=e^x-ax^2-(e-a-1)x-1$ 在 $(0,1)$ 上有零点,求 $a$ 范围。
有 $f(0)=f(1)=0,f'(x)=e^x-2ax-(e-a-1),f''(x)=e^x-2a,f'''(x)=e^x>0$,同样得出分段点 $\displaystyle e-2,1,\frac{1}{2},\frac{e}{2}$,答案 $(e-2,1)$.
- 因此我们得出结论:若 $f(x)$ 在 **闭区间** $[a,b]$ 上有 $m$ 个不同的零点,则 $f'(x)$ 至少 $m-1$ 个零点,$f''(x)$ 至少 $m-2$ 个零点,$\dots$。也就是说,**每求一次导其零点的个数至多减少 $1$ 个**。注意此结论不可逆推。
如果题目给开区间:**判断端点是否是零点!** 如第 $3$ 题,$f(1)=0,f(0)\neq 0$,所以 $f(x)$ 在 $[0,1]$ 至少 $2$ 个零点,$f'(x)$ 至少 $1$ 个零点。
### B
以下给出一个约定:不管 $f(x)$ 在区间的端点 $a$ 处是否有意义,也不管 $a$ 是否为 $\pm\infty$,都记 $f(a)$ 为 $x\to a$ 时的值。
- 广义零点存在定理:如果 $f(x)$ 在 $(a,b)$ 上连续,**且在区间端点不一定有意义**,若 $f(a)f(b)<0$,则 $f(x)$ 在 $(a,b)$ 上有零点。
---
1. $f(x)=\ln x+\sin x$,找出一个 $x_0\in(0,+\infty)$ 使得 $f(x_0)<0$.
$\ln x+\sin x<0\implies \ln x<-\sin x\implies \ln x<-1<\sin x\implies 0<x<e^{-1}$
因此,$x=e^{-1}$ 满足题意。此外,中间插入的数不但可以是 $1$,也可以是 $\displaystyle-\frac{1}{2}$ 等。
如果这是一道解答题,只需把分析倒过来写即可。也就是所谓的“放缩”。
练习题:已知 $\displaystyle f(x)=\ln x-\frac{x+1}{x-1}$,找出一个 $x_0\in(0,1)$,使得 $f(x_0)>0$.
我们将题目变为 $\displaystyle\ln x>a>\frac{x+1}{x-1}\implies\begin{cases}\ln x>-1 \\ \displaystyle -1>\frac{x+1}{x-1}\end{cases}\implies \begin{cases}x>e^{-1}\\ 0<x<1\end{cases}$ 即可。
答案:$[e^{-1},1)$ 之间任意数。
---
- **内点效应**:函数 $f(x),g(x)$ 定义在 $(a,b)$ 上。
$(1)$ 若 $f(a)>g(a)$,则任选 $t\in(g(a),f(a))$,不等式组 $\begin{cases}f(x)>t\\t>g(x)\end{cases}$ 都有解,而且这个解集中的任意一点都满足 $f(x)>g(x)$.
$(2)$ 若 $f(a)<g(a)$,则任选 $t\in(g(a),f(a))$,不等式组 $\begin{cases}f(x)<t\\t<g(x)\end{cases}$ 都有解,而且这个解集中的任意一点都满足 $f(x)<g(x)$.
---
2. 已知 $\displaystyle a>0,f(x)=x^2+\frac{3}{x}-a$,找到一个 $x_0\in(-\infty,0)$ 使得 $f(x_0)>0$.
答案:$x_0<\min\set{-\sqrt{a+1},-3}$.
练习题:设 $\displaystyle 0<a<\frac{1}{e},f(x)=\frac{1}{x}-axe^x$,找到一个 $x_0\in(0,+\infty)$ 使得 $f(x_0)<0$.
答案:可取 $-\ln a$. ( 不唯一 )
3. 已知 $f(x)=(2-a)(x-1)-2\ln x$ 在 $\displaystyle\left(0,\frac{1}{2}\right)$ 上无零点,求 $a$ 范围。
【分析】因为 $f(0^+)=+\infty$ 且 $f(x)$ 在 $\displaystyle\left(0,\frac{1}{2}\right)$ 上无零点,所以 $\displaystyle f\left(\frac{1}{2}\right)\geq 0\implies a\geq 2-4\ln 2$.
$\displaystyle f'(x)=2-a-\frac{2}{x}\ \uparrow\implies f'(x)\leq f'\left(\frac{1}{2}\right)=-2-a<0$,即此时 $f(x)\downarrow$,无零点。
现在我们再分析 $a<2-4\ln 2$ 的情况。
我们有 $(2-a)(x-1)>2\ln x$,$x\to 0$ 时,左边趋于 $a-2$,右边趋于 $-\infty$. 令 $\begin{cases}(2-a)(x-1)>a-3\\a-3>2\ln x\end{cases}$,当 $a>2$ 时,解得 $\displaystyle 0<x<\min\set{\frac{1}{a-2},e^{\frac{a-3}{2}}}$,当 $a\geq 2$ 时,解得 $\displaystyle x<e^{\frac{a-3}{2}}$.
【解析】
因为 $f(x)$ 在 $\displaystyle \left(0,\frac{1}{2}\right)$ 上无零点,所以 $\displaystyle f\left(\frac{1}{2}\right)\geq 0$ 得 $a\geq 2-4\ln 2$.
$(1)$ 当 $a\leq 2$ 时,取 $\displaystyle x_1=e^{\frac{a-3}{2}}$,则 $a-3=2\ln x_1$ 且 $(2-a)(x_1-1)>a-3$,即 $f(x_1)>0$,解得 $2-4\ln 2\leq a\leq 2$.
$(2)$ 当 $a>2$ 时,取 $\displaystyle x_2=\min\set{\frac{1}{a-2},e^{\frac{a-3}{2}}}$,则 $a-3>2\ln x_2$ 且 $(2-a)(x_2-1)>a-3$,即 $f(x_2)>0$,解得 $a>2$.
综上 $a\in[2-4\ln 2,+\infty)$.
### C
To Be Done.
## 分离变量
含有参数的函数图像极难画出,因此这时候就需要尽可能将参数分离出去,转化为水平直线与曲线交点问题。
例题:【2023 HB 文 T10】已知函数 $f(x)=x(\ln x-ax)$ 有 $2$ 个极值点,求 $a$ 的取值范围。
首先明确定义域 $x\in(0,+\infty)$.
由题意得 $f'(x)=\ln x-2ax+1=0$ 有 $2$ 个零点,则把 $a$ 分离出来得 $\displaystyle a=\frac{\ln x+1}{2x}$.
令 $\displaystyle g(x)=\frac{\ln x +1}{x},g'(x)=-\frac{\ln x}{x^2}\implies\begin{cases}
0 < x<1 & g'(x) > 0 & \ \ \ \ g(x) \uparrow \\
x>1 & g'(x)<0 & \ \ \ \ g(x) \downarrow
\end{cases}$
所以 $g(x)$ 在 $x=1$ 处取得最大值 $g(1)=1$.
要使 $f(x)$ 有 $2$ 个极值点,相当于使直线 $y=a$ 与 $\displaystyle\frac{1}{2}g(x)$ 有 $2$ 个交点。
那么很明显 $0<2a<1$,答案是 $\displaystyle\left(0,\frac{1}{2}\right)$.
练习题:函数 $\displaystyle f(x)=\frac{1}{4}x^4+x^3-\frac{9}{2}x^2+cx$ 有 $3$ 个极值点,证明:$-27<c<5$.
## 同构
先来一些简单题。
【2025 T8 联考 T17】设 $\displaystyle f(x)=\frac{1}{2}x^2-\frac{5}{2}x+\ln x$,证明:$\displaystyle f(x)-\frac{1}{2}x^2+\frac{7}{2}x\leq xe^{x+1}-2$.
也就是证明 $x+\ln x\leq xe^{x+1}-2$,变为
$$x+\ln x+1\leq e^{x+\ln x+1}-1$$
$$e^{x+\ln x+1}\leq x+\ln x+1$$
显然上述成立。
---
已知 $k>0$,若对任意的 $\displaystyle x\in\left[\frac{1}{e},+\infty\right)$,不等式 $e^{kx}(kx-\ln 2)-2x\ln x\geq 0$ 恒成立,则实数 $k$ 的最小值为 ?
$$e^{kx-\ln 2}(kx-\ln 2)\geq e^{\ln x}\ln x\implies k_{\min}=\frac{2}{e}$$
---
若关于 $x$ 的方程 $\displaystyle\frac{x}{e^x}+\frac{e^{x+1}}{x+e^x}+m=0$ 有三个不等实数解 $x_1,x_2,x_3$,且 $x_1<0<x_2<x_3$,则 $\displaystyle \left(\frac{x_1}{e^{x_1}}+1\right)^2\left(\frac{x_2}{e^{x_2}}+1\right)\left(\frac{x_3}{e^{x_3}}+1\right)$ 的值为 ?
$$\frac{x}{e^x}+\frac{e^{x+1}}{x+e^x}=\frac{x}{e^x}+\frac{e}{\frac{x}{e^x}+1}$$
### 构造函数
| 序号 | 模型 | 构造函数 |
|:-:|:-:|:-:|
| $1$ | $f'(x)>k\ (k\neq 0)$ | $g(x)=f(x)-kx+b$ |
| $2$ | $xf'(x)\pm nf(x)>0$ | $g(x)=x^{\pm n}f(x)$ |
| $3$ | $f'(x)+\ln a\cdot f(x)>0$ | $g(x)=a^xf(x)$ |
| $4$ | $\displaystyle\frac{f'(x)}{f(x)}>0$ | $g(x)=\ln \|f(x)\|$ |
这 $4$ 种模型是基本要掌握的,其他的一般可以盯出来。
## 极值点偏移
左偏:图像左陡右缓,$f(x_1)=f(x_2)\implies x_1+x_2>2x_0$
右偏:图像左缓右陡,$f(x_1)=f(x_2)\implies x_1+x_2<2x_0$
4 种题型:$x_1+x_2>2x_0,x_1+x_2<2x_0,x_1x_2<x_0^2,x_1x_2>x_0^2$
3 种方法:
1. 差值 / 比值代换,令 $t=x_2-x_1>0$ 或 $\displaystyle t=\frac{x_2}{x_1}>1$,把其他的量都以 $t$ 表示。
2. 对均不等式:$$\red{\boxed{\sqrt{x_1x_2}<\frac{x_1-x_2}{\ln x_1-\ln x_2}<\frac{x_1+x_2}{2}}}\ \ \ \ \ \ \ \ \ \ x_1>x_2>0$$
3. 构造对称“差函数”:$F(x)=f(x)-f(2x_0-x)$ 或 $\displaystyle F(x)=f(x)-f\left(\frac{x_0^2}{x}\right)$
- 对均不等式证明:
左边:令 $\displaystyle t=\frac{x_1}{x_2},x_1=tx_2$,原式化为 $\displaystyle\sqrt{tx_1x_2}<\frac{tx_2-x_2}{\ln(tx_2)-\ln x_2}\implies \sqrt{t}<\frac{t-1}{\ln t}$,只要证明 $\displaystyle f(t)=\ln t-\frac{t-1}{\sqrt{t}}<0$ 即可。$\displaystyle f'(t)=-\frac{(\sqrt{t}-1)^2}{2t\sqrt{t}}<0,f(t)<f(1)=0$.
右边:令 $\displaystyle t=\frac{x_1}{x_2},x_1=tx_2$,原式化为 $\displaystyle\frac{tx_2-x_2}{\ln(tx_2)-\ln x_2}<\frac{tx_2+x_2}{2}\implies \frac{t-1}{\ln t}<\frac{t+1}{2}$,只要证明 $\displaystyle g(t)=\ln t-\frac{2(t-1)}{t+1}>0$ 即可。$\displaystyle g'(t)=\frac{(t-1)^2}{t(t+1)^2}>0,g(t)>g(1)=0$.
---
例 1:$f(x)=e^x-ax$ 有两个零点 $x_1,x_2$,证明 $x_1+x_2>2$.
1. 差值代换:$x_1>x_2,t=x_1-x_2>0,x_1=x_2+t,\displaystyle\because\begin{cases}e^{x_1}=ax_1\\e^{x_2}=ax_2\end{cases}\\\therefore\begin{cases}a(x_1+x_2)=e^{x_1}+e^{x_2}\\a(x_1-x_2)=e^{x_1}-e^{x_2}\end{cases}\implies x_1+x_2=\frac{(x_1-x_2)(e^{x_1}+e^{x_2})}{e^{x_1}-e^{x_2}}=\frac{(x_1-x_2)(e^{x_1-x_2}+1)}{e^{x_1-x_2}-1}=\frac{t(e^t+1)}{e^t-1}$
只要证 $\displaystyle\frac{t(e^t+1)}{e^t-1}>2$ 即可,导两次可证,亦可用不等式 $\displaystyle t>\frac{2(e^t-1)}{e^t+1}$ 得到。
2. 比值代换:$\displaystyle x_1>x_2,t=\frac{x_1}{x_2}>1,x_1=tx_2,\displaystyle\because\frac{e^{x_1}}{x_1}=\frac{e^{x_2}}{x_2},\therefore x_1=\frac{t\ln t}{t-1},x_2=\frac{\ln t}{t-1}\\x_1+x_2=\frac{(t+1)\ln t}{t-1}$,只要证 $\displaystyle\frac{(t+1)\ln t}{t-1}>2$ 即可。
3. 对均不等式:由 $\begin{cases}e^{x_1}=ax_1\\e^{x_2}=ax_2\end{cases}$ 得 $\begin{cases}x_1=\ln a+\ln x_1\\x_2=\ln a+\ln x_2\end{cases}$ 得 $x_1-x_2=\ln x_1-\ln x_2$.
4. 构造差函数:$\displaystyle f(x)=0\implies a=\frac{e^x}{x}=g(x),g(x_1)=g(x_2),g'(x)=\frac{(x-1)e^x}{x^2}$
$g(x)$ 在 $(0,1)\downarrow(1,+\infty)\uparrow$,设 $0<x_1<1<x_2$,则
$$x_1+x_2>2\iff x_2>2-x_1>1\iff g(x_2)>g(2-x_1)\iff g(x_1)>g(2-x_1)$$
$h(x)=g(x)-g(2-x)\ (0<x<1),h'(x)=g'(x)+g'(2-x)<0$
$h(x)$ 在 $(0,1)\downarrow,h(x)>h(1)=0$,即 $g(x_1)>g(2-x_1)$ 恒成立。
练 1:证明 $x_1+x_2<2\ln a,0<x_1x_2<1$.
---
例 2:$f(x)=\ln x-ax$ 有两个零点 $x_1,x_2(x_1<x_2)$,证明 $\displaystyle \frac{2}{a}<x_1+x_2<\frac{2}{a^2e}$.
解:首先 $\displaystyle a\in\left(0,\frac{1}{e}\right)$,然后
$$\begin{cases}\ln x_1=ax_1\\\ln x_2=ax_2\end{cases}\implies \ln x_2-\ln x_1=a(x_2-x_1)\implies\frac{1}{a}=\frac{x_2-x_1}{\ln x_2-\ln x_1}<\frac{x_1+x_2}{2}$$
令 $\boxed{F(x)=e\ln^2x-2x}$ 为单调减函数,
$$F(x_1)>F(x_2)\iff e(\ln x_1+\ln x_2)(\ln x_2-\ln x_1)<2(x_2-x_1)\\\implies\frac{2}{a}>e(\ln x_1+\ln x_2)=ea(x_1+x_2)\implies x_1+x_2<\frac{2}{a^2e}$$
练 2:证明 $x_1x_2>e^2$. 更难的:证明 $\displaystyle x_1+x_2>\frac{10}{3a}-\frac{4e}{3}>\frac{3}{a}-e>\frac{2}{a}$.
---
( 切线夹 + 极值点偏移 )例 3:【2021 I 卷 T22】已知函数 $f(x)=x(1-\ln x)$.
$(1)$ 讨论 $f(x)$ 的单调性。
$(2)$ 设 $a,b$ 是两个不相等的正数,且 $b\ln a-a\ln b=a-b$,证明:$\displaystyle 2<\frac{1}{a}+\frac{1}{b}<e$.
解:$(1)\ f'(x)=-\ln x,f(x)$ 在 $(0,1)\uparrow,(1,+\infty)\downarrow$
$(2)$ $b\ln a-a\ln b=a-b\implies\displaystyle\frac{1}{a}\left(1-\ln\frac{1}{a}\right)=\frac{1}{b}\left(1-\ln\frac{1}{b}\right)\iff f\left(\frac{1}{a}\right)=f\left(\frac{1}{b}\right)$
显然,题目转化为 $g(x)=x\ln x-x-m$ 有两个零点 $x_1,x_2$,证明 $2<x_1+x_2<e$。
设 $x_1>x_2$,令 $\displaystyle \boxed{h(x)=x\ln x-\frac{x^2}{2}},h'(x)=\ln x+1-x\leq 0\implies h(x_1)<h(x_2)$。
$$x_1\ln x_1-\frac{x_1^2}{2}<x_2\ln x_2-\frac{x_2^2}{2}\implies x_1\ln x_1-x_2\ln x_2<\frac{1}{2}(x_1+x_2)(x_1-x_2)$$
由已知 $x_1\ln x_1-x_2\ln x_2=x_1-x_2>1$,故 $x_1+x_2>2$。
令 $\displaystyle i(x)=x+f(x)=2x-x\ln x,i'(x)=1-\ln x$ 得 $i(x)<i(e)=e$ 得 $x_2+f(x_2)<e$.
因 $x_1\in(0,1)$,所以 $x_1<x_1(1-\ln x_1)=f(x_1)=f(x_2)$,所以 $x_1+x_2<f(x_2)+x_2<e$.
类似方框中的增强函数:
| 序号 | $f(x)$ | $f'(x)$ |
|:-:|:-:|:-:|
| $1$ | $\displaystyle x\ln x-\frac{x^2}{2}$ | $\displaystyle \ln x+1-x\leq 0$ |
| $2$ | $\displaystyle x\ln x+\ln x-2x$ | $\displaystyle \ln x-1+\frac{1}{x}\geq 0$ |
| $3$ | $\displaystyle \frac{1}{2}x^2\ln x+x-\frac{3x^2}{4}$ | $\displaystyle x\ln x-x+1\geq 0$ |
| $4$ | $\displaystyle e\ln^2x-2x$ | $\displaystyle \frac{2(e\ln x-x)}{x}\leq 0$ |
| $5$ | $\displaystyle ex-\ln x-ex\ln x$ | $\displaystyle -\frac{ex\ln x+1}{x}\leq 0$ |
练 3:已知 $x\ln x=m$ 有两根 $x_1,x_2$,证明 $\displaystyle x_1+x_2>\frac{2}{e}$.
练 4:已知 $\displaystyle x^2\ln x-\frac{x^2}{2}=m$ 有两根 $x_1,x_2$,证明 $\displaystyle x_1+x_2<2$.( 增强函数 $3$ )
练 5:已知 $x^2\ln x=m$ 有两根 $x_1,x_2$,证明 $\displaystyle x_1+x_2<\frac{2}{\sqrt{e}}$.
---
例 4:【ZJ 9+1 联盟】$x-\ln x=a$ 有两根 $x_1,x_2$,证明 $x_1+x_2>a+1$.
目标变成
$$(x_1+x_2)(x_1-x_2)>(a+1)(x_1-x_2)\iff x_1^2-(a+1)x_1>x_2^2-(a+1)x_2\\ \iff x_1(x_1-a-1)>x_2(x_2-a-1)\iff x_1(\ln x_1-1)>x_2(\ln x_2-1)$$
选用增强函数 $2$,令 $F(x)=x\ln x-x-(x-\ln x)=x\ln x+\ln x-2x$ 为单调增函数,由 $F(x_1)>F(x_2)$ 即得答案。
为什么这样构造 ?“极值点偏移”及其衍生问题的本质,就是在一个增强函数中拆分出两个或多个极值点相同的单峰子函数,对其中一个子函数赋予一个等式条件,要求证明另一个子函数的相关不等关系。这个母函数应满足如下要求:
1. 在定义域内单调
2. 导数有零点,且与子函数的极值点一致( 这样能够保证增强函数在导数零点附近的增减趋势极其平缓,使不等式的精度达到最大 )
我们随便出一题:
1. 确定一个常用不等式:$\displaystyle x^2\ln x\geq -\frac{1}{2e}\ \ \ \ (\ x=\frac{1}{\sqrt{e}}$ 取等 $)$
2. 适当变形构造函数:$\displaystyle F'(x)=\frac{2ex^2\ln x+1}{x^2}\geq 0$
3. 求原函数( 增强函数 ):$\displaystyle F(x)=2ex\ln x-2ex-\frac{1}{x}$
4. 在增强函数中剔除 $f(x)=2ex\ln x-ex$,极值点为 $\displaystyle x=\frac{1}{\sqrt{e}}$,$\displaystyle F(x)=2ex\ln x-ex-(ex+\frac{1}{x})$. 那么 $\displaystyle g(x)=ex+\frac{1}{x}$ 极值点也为 $\displaystyle x=\frac{1}{\sqrt{e}}$!
5. 给 $f(x)$ 赋予等式:$2x_1\ln x_1-x_1=2x_2\ln x_2-x_2$,由 $x_1>x_2,F(x_1)>F(x_2)$ 得 $g(x_1)<g(x_2)$,变成 $\displaystyle x_1x_2<\frac{1}{e}$.
6. 简单包装变为:设 $\displaystyle f(x)=2\ln x-\frac{m}{x}-1$ 有两个零点 $x_1,x_2$,证明:$\displaystyle x_1x_2<\frac{1}{e}$.
对于本题,设 $\displaystyle F(x)=x\ln x-x-k(x-\ln x),F'(x)=\ln x-k\left(1-\frac{1}{x}\right),F''(x)=\frac{1}{x}-\frac{k}{x^2}$,由 $F'(1)=0$ 得 $F''(1)=0$ 得 $k=1$.
那么怎么构造增强函数呢 ?我们需要先知道一个定理:[here](https://zhuanlan.zhihu.com/p/6010455015?utm_psn=1842528072357769220)
若给定函数 $f(x),g(x)$ 使得 $\exist x_0\ s.t.\ f'(x_0)=g'(x_0)=0,f''(x_0)\neq 0,g''(x_0)\neq 0$
$\exist x_1\neq x_2\ s.t.\ f(x_1)=f(x_2),\forall x,\displaystyle\frac{f'''(x)}{f''(x_0)}>\frac{g'''(x)}{g''(x_0)}$,则 $\displaystyle\frac{g(x_1)-g(x_2)}{x_1-x_2}g''(x_0)<0$
证明通过设 $\displaystyle L(x)=\frac{f(x)}{f''(x_0)}-\frac{g(x)}{g''(x_0)}$,求三阶导证。
若我们取 $g(x)=h^2(x)-2h(x_0)h(x)$,则最后的不等式变为
$$[h(x_1)+h(x_2)-2h(x_0)]\frac{h(x_1)-h(x_2)}{x_1-x_2}<0$$
通常最后一项的正负是确定的,这正是极值点偏移的形式。
例题:已知 $x_1-\ln x_1=x_2-\ln x_2=m,x_1>x_2$,证 $x_1+x_2>m+1$.
首先 $\displaystyle f(x)=x-\ln x,f'(x)=1-\frac{1}{x},f''(x)=\frac{1}{x^2},x_0=1$
要证 $(x_1+x_2)(x_1-x_2)>(m+1)(x_1-x_2)\implies x_1^2-(m+1)x_1>x_2^2-(m+1)x_2$
设 $g(x)=x^2-(m+1)x,g'(x)=2x-(m+1),g''(x)=2$,得出 $\displaystyle L(x)=\frac{f(x)}{f''(x_0)}-\frac{g(x)}{g''(x_0)}=2x-x\ln x-\ln x,L'(x)=1-\ln x-\frac{1}{x}\leq 0\implies L(x)\downarrow,L(x_1)>L(x_2)$
即 $2x_1-x_1\ln x_1-\ln x_1>2x_2-x_2\ln x_2-\ln x_2$,稍加变换即得到答案。
练习 1:同样是上面的等式关系,证明 $①x_1+x_2+2x_1x_2>4\ ②x_1+x_2<\frac{4m+2}{3}\ ③\displaystyle x_1x_2<\frac{2}{m+1}$
需要构造的函数中 $\displaystyle ②L(x)=x-\ln x+\frac{1}{2}x(x-4\ln x+2)$
练习 2:已知 $x\ln x=m$ 的两根 $x_1,x_2$,证明 $\displaystyle x_1+x_2>\frac{2}{e}$
需要构造的函数为 $\displaystyle L(x)=\frac{x(\ln x+1)}{e}-\frac{x^2}{2}$
---
例 5:$f(x)=x\ln x-ax-a$,若存在 $0<x_1<x_2$ 使得 $f(x_1)=f(x_2)$,证明:$x_1+x_2+\sqrt{x_1x_2}<3e^{a-1}$.
$$x_1\ln x_1-ax_1=x_2\ln x_2-ax_2\implies\frac{x_1}{e^a}\ln\frac{x_1}{e^a}=\frac{x_2}{e^a}\ln\frac{x_2}{e^a}\xRightarrow{\frac{x}{e^a}\to x}x_1\ln x_1=x_2\ln x_2$$
只用证 $\displaystyle x_1+x_2+\sqrt{x_1x_2}<\frac{3}{e}$ 即可,设 $x_2=t^2x_1(t>1)$,得到 $\displaystyle \ln x_1=\frac{2t^2\ln t}{1-t^2}$,要证 $\displaystyle x_1(1+t+t^2)<\frac{3}{e}$,即证 $\displaystyle (t^2-1)\ln\frac{t^2+t+1}{3}<2t^2\ln t-t^2+1$,二阶导证明即可,得到海伦幂平均不等式。
---
一些常用结论:
- 海伦幂平均不等式:$\forall a,b\in\R^+,a\neq b,$
$$\frac{1}{e}\cdot\left(\frac{a^a}{b^b}\right)^{\displaystyle\frac{1}{a-b}}>\frac{a+b+\sqrt{ab}}{3}$$
两边取对数得到
$$\frac{a\ln a-b\ln b}{a-b}-1>\ln\frac{a+b+\sqrt{ab} }{3}$$
取 $b=1$ 得到
$$\frac{x\ln x}{x-1}-1\geq \ln\frac{x+1+\sqrt{x} }{3}$$
## 好题
已知函数,$f(x)=e^{-x}+\cos x-ax,g(x)$ 为 $f(x)$ 的导函数。
$(1)$ 证明:当 $a=0$ 时,函数 $g(x)$ 在区间 $\displaystyle\left[0,\frac{\pi}{2}\right]$ 内存在唯一的极值点 $x_0$;
$(2)$ 若 $\displaystyle H(x)=f(x)-\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)$,且 $H(x)$ 在 $(0,2\pi)$ 上单调递减,求 $a$ 范围。
解:$(1)\ f(x)=e^{-x}+\cos x,f'(x)=-e^{-x}-\sin x,f''(x)=e^{-x}-\cos x,f'''(x)=-e^{-x}+\sin x$
$f'''(x)$ 在 $\displaystyle\left[0,\frac{\pi}{2}\right]\uparrow,f'''(0)=-1,f'''\left(\frac{\pi}{4}\right)>0$,故 $f'''(x)$ 在 $\displaystyle\left[0,\frac{\pi}{4}\right]$ 上存在零点 $x_1$ 且 $e^{-x_1}=\sin x_1$.
$f''(x)$ 先 $\downarrow$ 后 $\uparrow$,$f''(x_1)=e^{-x_1}-\cos x_1=\sin x_1-\cos x_1<0$,而 $\displaystyle f''(0)=0,f''\left(\frac{\pi}{2}\right)>0$,故 $f''(x)$ 在 $\displaystyle\left[0,\frac{\pi}{2}\right]$ 上存在零点,故得证。
$(2)\ H(x)=e^{-x}+\cos x-ax-\cos x+\sin x=e^{-x}+\sin x-ax,H'(x)=-e^{-x}+\cos x-a$ 要在 $(0,2\pi)<0$,只用 $a\geq \varphi(x)=-e^{-x}+\cos x$ 即可。 $\varphi'(x)=e^{-x}-\sin x,\varphi''(x)=-e^{-x}-\cos x$.
$\varphi'(x)$ 在 $(\pi,2\pi)>0,\varphi(x)\uparrow$,在 $(0,\pi)$ 存在零点 $\displaystyle x_1\in\left(0,\frac{3\pi}{4}\right)$ 满足 $\varphi''(x_1)=0\to e^{-x_1}+\cos x_1=0,\varphi'(0)=1>0,\varphi'(\pi)>0$,故必存在 $x_2\in(0,x_1),x_3\in(x_1,\pi)$ 使得 $\varphi'(x_2)=\varphi'(x_3)=0$.
$\varphi(x)$ 在 $(0,x_2)\uparrow,(x_2,x_3)\downarrow,(x_3,2\pi)\uparrow$,而 $\varphi(x_2)=-e^{-x_2}+\cos x_2<\varphi(2\pi)=-e^{-2\pi}+1$,故答案为 $\displaystyle a\in[1-e^{-2\pi},+\infty)$.
---
$\displaystyle f(x)=\frac{\sin x}{2+\cos x}$,如果对 $\forall x\geq 0$,都有 $f(x)\leq ax$,求 $a$ 范围。
即 $a\geq\displaystyle\frac{\sin x}{x(2+\cos x)}=g(x),g'(x)=\frac{2x\cos x-2\sin x-\sin x\cos x+x}{x^2(2+\cos x)^2}$.
令 $h(x)=2x\cos x-2\sin x-\sin x\cos x+x,h'(x)=2\sin x(\sin x-x)$ 在 $(0,\pi)$ 时 $<0$,故 $\varphi(x)<\varphi(0)=0,h(x)\downarrow$。我们利用洛必达法则,
$$\lim_{x\to 0}\frac{\sin x}{x(2+\cos x)}=\lim_{x\to 0}\frac{\cos x}{2+\cos x-x\sin x}=\frac{1}{3}$$
所以在 $(0,\pi]$ 内 $\displaystyle a\geq \frac{1}{3}$,在 $(\pi,+\infty)$ 内,$\displaystyle\frac{\sin x}{2+\cos x}<1,g(x)\leq \frac{1}{x}\leq \frac{1}{\pi}<\frac{1}{3}$.
所以 $\displaystyle a\in\left[\frac{1}{3},+\infty\right)$.
---
设函数 $f(x)=\ln x-a(x-1)e^x$,其中 $a\in\R$ 且 $\displaystyle 0<a<\frac{1}{4}$,$x_0$ 为 $f(x)$ 极值点,$x_1$ 为 $f(x)$ 零点,且 $x_1>x_0$,证明:$3x_0-x_1>2$.
$\displaystyle f'(x)=\frac{1}{x}-axe^x\implies x_0^2e^{x_0}=\frac{1}{a},\ln x_1=a(x_1-1)e^{x_1}=\frac{x_1-1}{x_0^2}e^{x_1-x_0}\\\implies e^{x_1-x_0}=\frac{x_0^2\ln x_1}{x_1-1}<x_0^2$,两边取对数即证。
---
当 $x\in(0,1)$ 时,证明:$\displaystyle x^2+x-\frac{1}{x}-1<e^x\ln x$.
由 $\ln x\leq x-1$ 得 $\displaystyle -\ln x\leq\frac{1}{x}-1$,只用证 $\displaystyle LHS<(1-\frac{1}{x})e^x$,变为 $(x+1)^2>e^x$.
---
设 $n\in\N^*$,证明 $\displaystyle\sum_{k=1}^n\frac{1}{(n+k)\tan\frac{1}{n+k}}>n-\frac{1}{4n+2}$.
$$\frac{\cos\frac{1}{n+k}}{(n+k)\sin\frac{1}{n+k}}>\cos\frac{1}{n+k}>1-\frac{1}{2(n+k)^2}$$
只用证
$$\sum_{k=1}^n\frac{1}{(n+k)^2}<\frac{1}{2n+1}$$
由以下得证:
$$\frac{1}{(n+k)^2}<\frac{1}{(n+k-1)(n+k+1)}=\frac{1}{2}\left(\frac{1}{n+k-1}-\frac{1}{n+k+1}\right)$$
# 统计
简单随机抽样:$1.$ 个体数有限 $2.$ 逐个抽取 $3.$ 被抽到的概率相等。
例:$10$ 个个体里抽一个容量为 $n$ 的样本, 某个个体 $A$ 第一次被抽到的可能性为 ?第二次被抽到的可能性为 ?
第一次:$\displaystyle\frac{1}{10}$ 第二次:$\displaystyle\frac{9}{10}\times\frac{1}{9}=\frac{1}{10}$
随机数表题:范围 $[0,39]$,有以下随机数表,从第 $1$ 行第 $3$ 列开始,选出的数依次为 $36,33,26,16,11,14,10$.
| $0347$ | $4373$ | $8636$ | $9647$ | $3661$ | $4698$ |
|:-:|:-:|:-:|:-:|:-:|:-:|
| $6371$ | $6233$ | $2616$ | $8045$ | $6011$ | $1410$ |
总体平均数:$\displaystyle\bar{x}=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i\ \ \text{}$ 中位数:$\begin{cases}x_{\lceil\frac{n}{2}\rceil} & x\ \mathrm{mod}\ 2\equiv 1 \\ \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} & x\ \mathrm{mod}\ 2\equiv 0\end{cases}\ \ \text{}$
众数:出现次数最多的数据,不一定唯一,也不一定有众数。
极差:$\max{\set{x_i}}-\min{\set{x_i}}\ \ \ \ \text{}$ 标准差:$s=\sqrt{\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2}$
$\begin{aligned}方差:s^2&=\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2=\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i^2-2x_i\bar{x}+\bar{x}^2)=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i^2-\frac{1}{n}\displaystyle\sum_{i=1}^{n}2x_i\bar{x}+\frac{1}{n}\displaystyle\sum_{i=1}^{n}\bar{x}^2\\&=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i^2-2\bar{x}^2+\bar{x}^2=\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_i^2-\bar{x}^2\end{aligned}$
残差 $=$ 实际值 $-$ 观测值
若采用分层随机抽样,分 $n$ 层,样本数 $m_1,m_2,\dots,m_n$,平均值 $x_1,x_2,\dots,x_n$,$\\$ 则样本平均数 $\bar{x}=\displaystyle\sum_{i=1}^{n}\frac{m_i\cdot x_i}{\displaystyle\sum_{j=1}^{n}m_j}$,注意样本平均数 $\neq$ 总体平均数。
分层随机抽样需按比例分配:$\frac{总体中第\ m\ 层个体数}{总体中第\ n\ 层个体数}=\frac{样本中第\ m\ 层个体数}{样本中第\ n\ 层个体数}$ 且 $\frac{样本中第\ m\ 层个体数}{总体中第\ m\ 层个体数}=\frac{样本容量}{总体容量}$
第 $p$ 百分位数:数据中至少有 $p\%$ 的数据 $\leq$ 这个值,至少有 $(100-p)\%$ 的数 $\geq$ 这个值。
第 $25$ 百分位数:第一四分位数 / 下四分位数;第 $75$ 百分位数:第三四分位数 / 上四分位数;第 $50$ 百分位数:中位数。
已知数据求第 $p$ 百分位数:1. 从小到大排序,令 $i=n\times p\%$ 2. $\begin{cases}\text{ans}=\frac{a_i+a_{i+1}}{2} & \lfloor i \rfloor = i \\ \text{ans}=a_{\lceil i \rceil} & \lfloor i \rfloor \neq i \end{cases}$
格式要求:$\begin{cases}[a,b) 的频率 <x\% \\ [a,c)的频率>x\%\end{cases}\implies$ 第 $x$ 百分位数在 $[b,c)$ 内。
$n$ 层构成样本的方差:$s^2=\displaystyle\sum_{i=1}^{n}w_i[s_i^2+(\bar{x}_i-\bar{x})^2]$,其中 $\bar{x}_i$ 为样本中不同层的平均数,$s_i^2$ 为不同层的方差,$w_i$ 为相应的权重( 该层样本数占总样本的多少,$w_i<1$ )
特别地,只有 $2$ 层时,若:
| 第 $1$ 层 | $m$ 个数 | $\bar x$ | $s^2$ |
|:-:|:-:|:-:|:-:|
| 第 $2$ 层 | $n$ 个数 | $\bar y$ | $t^2$ |
则总平均数 $\displaystyle\bar a=\frac{m\bar x+n\bar y}{m+n}$,总方差 $\displaystyle b^2=\frac{ms^2+nt^2+m(\bar x-\bar a)^2+n(\bar y-\bar a)^2}{m+n}$
若数据 $x_1,x_2,\dots,x_n$ 的平均数 $\bar x$,方差 $s^2$,标准差 $s$,则数据 $mx_1+a,mx_2+a,\dots,mx_n+a$ 的平均数 $m\bar{x}+a$,方差 $s^2m^2$,标准差 $sm$.
线性回归问题的一般步骤:( 最小二乘法 )
1. 列表 + 画散点图
| $x$ | $x_1$ | $x_2$ | $\dots$ | $x_n$ |
|:-:|:-:|:-:|:-:|:-:|
| $y$ | $y_1$ | $y_2$ | $\dots$ | $y_n$ |
2. 通过公式求 $\hat b,\hat a$.
$$\hat b=\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)^2}=\frac{\displaystyle\sum_{i=1}^{n} x_iy_i-n\bar x\bar y}{\displaystyle\sum_{i=1}^{n}x_i^2-n\bar x^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \hat a=\bar y-\hat b\bar x$$
3. 根据直线方程一定过 $\bar x,\bar y$ 得出 $\hat y=\hat bx+\hat a$.
如果散点均匀分布在回归直线的两侧,那么回归效果就好
如果 $\hat b > 0$ 则两变量正相关,反之则负相关,也可利用样本相关系数 $r$ 来判断。
$-1\leq r\leq 1,|r|$ 越接近 $1$,回归效果越好;$r>0$ 则正相关,$r<0$ 则负相关。
$$r=\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sqrt{\displaystyle\sum_{i=1}^{n}(x_i-\bar x)^2\sum_{i=1}^{n}(y_i-\bar y)^2}}=\frac{\displaystyle\sum_{i=1}^{n} x_iy_i-n\bar x\bar y}{\sqrt{\displaystyle\sum_{i=1}^{n}x_i^2-n\bar x^2}\sqrt{\displaystyle\sum_{i=1}^{n}y_i^2-n\bar y^2}}$$
非线性回归方程:转化为线性回归方程。
1. 幂函数型:$y=c_1x^{n}+c_2$
变换:令 $t=x^n,b=c_1,a=c_2$,则 $y=bt+a$.
2. 指数型:$y=c_1e^{c_2x}$
变换:两边取对数并令 $z=\ln y,a=\ln c_1,b=c_2$,则 $z=bx+a$.
变换后,需转化原函数关系,一般用相关指数来看拟合效果的强弱。( 注:非线性的不能用相关系数 $r$ )
- $2\times 2$ 列联表:形如这样的表
卡方( $\chi^2$ )独立性检验:
$$\chi=\frac{n(ad-bc)^2}{(a+b)(b+c)(a+c)(b+d)}$$
我们希望判断事件 $\set{X=1}$ 和 $\set{Y=1}$ 是否有关联,相当于判断下面的假定关系
$$H_0:\ \ \ P(Y=1|X=0)=P(Y=1|X=1)$$
是否成立,称 $H_0$ 为零假设或原假设。这里 $P(Y=1|X=0)$ 表示从 $\set{X=0}$ 中随机选一个样本点,该样本点属于 $\set{X=0,Y=1}$ 的概率。由条件概率,$H_0$ 等价于 $\set{X=1}$ 和 $\set{Y=1}$ 相互独立,进一步等价于 $X$ 和 $Y$ 独立。
对小概率值 $\alpha$ 的检验规则:
当 $\chi^2\geq x_{\alpha}$ 时,就推断 $H_0$ 不成立,$X$ 和 $Y$ 不独立。该推断犯错误的概率不超过 $\alpha$.
当 $\chi^2<x_{\alpha}$ 时,就推断 $H_0$ 成立,认为 $X$ 和 $Y$ 独立。
常用小概率值和临界值:
| $\alpha$ | $0.1$ | $0.05$ | $0.01$ | $0.005$ | $0.001$ |
|:-:|:-:|:-:|:-:|:-:|:-:|
| $x_\alpha$ | $2.706$ | $3.841$ | $6.635$ | $7.789$ | $10.828$ |
# 概率
### 基本概念
- 随机试验:对随机现象的实现和观察,用 $E$ 表示。
- 样本点:$E$ 的每个可能的基本结果,用 $\omega$ 表示。
- 样本空间:全体 $\omega$ 的集合,用 $\Omega$ 表示。
- 有限样本空间:若一个随机试验有 $n$ 个可能结果 $\omega_1,\omega_2,\dots,\omega_n$,则称样本空间 $\Omega=\set{\omega_1,\omega_2,\dots,\omega_n}$ 为有限样本空间 $\\$( 即 $\Omega$ 为有限集 )。
- 随机事件:$\Omega$ 的子集,简称事件,用大写字母 $A,B,C,\dots$ 表示,当且仅当 $A$ 中的某个样本点出现时,称事件 $A$ 发生。
- 基本事件:只包含一个样本点的事件。
- 必然事件:$\Omega$ 作为自身的子集,包含了所有样本点,在每次试验中总有一个样本点发生,即 $\Omega$ 总会发生。
- 不可能事件:$\varnothing$ 不含任何样本点,在每次试验中都不会发生,必然事件与不可能事件不具有随机性。
### 事件的关系和运算
| 事件的关系 | 含义 | 符号表示 |
| :-------------: | :-------------------------: | :---------------------------------------------: |
| 包含 | $A$ 发生 $\implies B$ 发生 | $A\subseteq B$ |
| 并事件 / 和事件 | $A$ 和 $B$ 至少一个发生 | $A\bigcup B$ 或 $A+B$ |
| 交事件 / 积事件 | $A$ 和 $B$ 同时发生 | $A\bigcap B$ 或 $AB$ |
| 互斥 / 互不相容 | $A$ 和 $B$ 不能同时发生 | $A\bigcap B=\varnothing$ |
| 互为独立 | $A$ 和 $B$ 有且仅有一个发生 | $A\bigcap B=\varnothing$ 且 $A\bigcup B=\Omega$ |
如果 $A,B$ 互斥,记 $\bar{A},\bar{B}$ 分别为 $A,B$ 的对立事件。
若 $A\subseteq B$ 且 $B\subseteq A$,则事件 $A$ 和事件 $B$ 相等,$A=B$.
对于三个事件 $A,B,C$,$A\bigcup B\bigcup C$ 或 $A+B+C$ 表示 $A,B,C$ 至少一个发生,其余同理。
### 古典概型
- 满足有限性( 有限样本空间 )、等可能性。
- 设 $E$ 为古典概型,样本空间 $\Omega$ 包含 $n$ 个样本点,事件 $A$ 包含其中的 $k$ 个样本点,则事件 $A$ 的概率为 $\displaystyle P(A)=\frac{k}{n}=\frac{n(A)}{n(\Omega)} \\ n(A),n(\Omega)$ 表示事件 $A$ 和样本空间 $\Omega$ 包含的样本点个数。
### 概率的基本性质
1. $\forall A,0\leq P(A)\leq 1$.
2. 必然事件 $\Omega$ 概率为 $P(\Omega)=1$,不可能事件 $\varnothing$ 概率为 $P(\varnothing)=0$.
3. 若 $A,B$ 互斥,则 $P(A\bigcup B)=P(A)+P(B)$; $\\$ 推广:若 $A_1,A_2,\dots,A_m$ 两两互斥,则 $P(A_1\bigcup A_2\bigcup\dots\bigcup A_m)=\displaystyle\sum_{i=1}^{m}P(A_i)$
4. 若 $A,B$ 对立,则 $P(B)=1-P(A),P(A)=1-P(B)$;若 $P(A)+P(B)=1$,则 $A,B$ 不一定对立。
5. 若 $A\subseteq B$,则 $P(A)\leq P(B)$( 概率的单调性 )
6. 设 $A,B$ 为随机试验中的两个事件,则 $P(A\bigcup B)=P(A)+P(B)-P(A\bigcap B)$ ( 容斥原理 )
7. 对任意 $2$ 个事件 $A,B$,若 $P(AB)=P(A)P(B)$,则 $A$ 与 $B$ 相互独立,记 $A,B$ 的对立事件分别为 $\bar{A},\bar{B}$ $\\$ 因事件 $A,B$ 的发生互不影响,则 $A$ 与 $\bar{B}$,$\bar{A}$ 与 $B$,$\bar{A}$ 与 $\bar{B}$ 也相互独立。
8. 若 $A,B,C$ 两两独立,则 $P(ABC)\neq P(A)P(B)P(C)$.
9. $\bar{A}\cap\bar{B}=\overline{A\cup B},\bar{A}\cup\bar{B}=\overline{A\cap B}$
| 事件含义 | 事件表示 | 概率 | $A,B$ 互斥 | $A,B$ 相互独立 |
| :---------------------: | :-----------------: | :--------------------------: | :-------------: | :-----------------------------: |
| $A$ 和 $B$ 至少一个发生 | $A\bigcup B$ | $P(A\bigcup B)$ | $P(A)+P(B)$ | $1-P(\bar{A})P(\bar{B})$ |
| $A$ 和 $B$ 同时发生 | $AB$ | $P(AB)$ | $0$ | $P(A)P(B)$ |
| $A$ 和 $B$ 都不发生 | $\bar{A}\bar{B}$ | $P(\bar{A}\bar{B})$ | $1-[P(A)+P(B)]$ | $P(\bar{A})P(\bar{B})$ |
| $A$ 和 $B$ 只有一个发生 | $A\bar{B}+\bar{A}B$ | $P(A\bar{B}\bigcup\bar{A}B)$ | $P(A)+P(B)$ | $P(A)P(\bar{B})+P(\bar{A})P(B)$ |
### 条件概率
一般地,设 $A,B$ 为两个随机事件,且 $P(A)>0$,那么
$$P(B|A)=\frac{P(AB)}{P(A)}$$
表示在事件 $A$ 发生的条件下,事件 $B$ 发生的概率。
反过来,对任意两个事件 $A,B$,若 $P(A)>0$,则有概率的乘法公式:
$$P(AB)=P(A)P(B|A)$$
条件概率具有的性质:
1. $P(\Omega|A)=1$.
2. 如果 $B,C$ 互斥,则 $P(B\bigcup C|A)=P(B|A)+P(C|A)$.
3. $P(\bar B|A)=1-P(B|A)$.
4. 已知 $P(A)>0,P(B)>0,P(B|A)=P(B)$,则 $P(A|B)=P(A)$.
5. 当 $P(AB)>0$ 时,$P(ABC)=P(A)P(B|A)P(C|AB)$. 推广开来,
$$P(A_1A_2\dots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\dots P(A_n|A_1A_2\dots A_{n-1})$$
### 全概率公式
设 $A_1,A_2,\dots,A_n$ 是两两互斥的事件且 $A_1\bigcup A_2\bigcup \dots\bigcup A_n=\Omega$ 且 $P(A_i)>0,i=1,2,\dots,n$,则对任意事件 $B\sube\Omega$ 有:
$$P(B)=\sum_{i=1}^nP(A_i)P(B|A_i)$$
教材例题:有 $3$ 台车床加工同一型号的零件,第 $1$ 台加工的次品率为 $6\%$,其余两台均为 $5\%$,加工出来的零件混放在一起。已知第 $1,2,3$ 台车床加工的零件数分别占总数的 $25\%,30\%,45\%$.
$(1)$ 任取一个零件,计算它是次品的概率。
$(2)$ 如果取到的是次品,计算它是第 $i(i=1,2,3)$ 台机床加工的概率。
解析:设 $B=$ “任取一个零件为次品”,$A_i=$ “零件为第 $i$ 台车床加工”,则 $\Omega=A_1\bigcup A_2\bigcup A_3$ 且 $A_1,A_2,A_3$ 两两互斥,根据题意有
$$P(A_1)=0.25,P(A_2)=0.3,P(A_3)=0.45$$
$$P(B|A_1)=0.06,P(B|A_2)=P(B|A_3)=0.05$$
$(1)$ 由全概率公式,
$$P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3)=0.0525$$
$(2)$ $\displaystyle P(A_1|B)=\frac{P(A_1B)}{P(B)}=\frac{2}{7}$,同理 $\displaystyle P(A_2|B)=\frac{2}{7},P(A_3|B)=\frac{3}{7}$.
---
将上题中 $(2)$ 一般化可以得到贝叶斯公式:( 这部分为人教版选学内容 )
设 $A_1,A_2,\dots,A_n$ 是两两互斥的事件且 $A_1\bigcup A_2\bigcup \dots\bigcup A_n=\Omega$ 且 $P(A_i)>0,i=1,2,\dots,n$,则对任意事件 $B\sube\Omega,P(B)>0$ 有:
$$P(A_i|B)=\frac{P(A_i)P(B|A_i)}{P(B)}=\frac{P(A_i)P(B|A_i)}{\displaystyle\sum_{k=1}^nP(A_k)P(B|A_k)}$$
### 离散型随机变量及其分布列
一般地,对于随机试验样本 $\Omega$ 中的每个样本点 $\omega$,都有唯一的实数 $X(\omega)$ 与之对应,我们称 $X$ 为随机变量。而可能取值为有限个的随机变量称之为 **离散型随机变量**。用大写字母表示随机变量,用小写字母表示随机变量的取值。
例如,投一枚质地均匀的骰子,事件抛出 $m$ 点可以表示为 $\set{X=m}(m=1,2,3,4,5,6)$,并且有 $\displaystyle P(X=m)=\frac{1}{6}$.
一般地,设离散型随机变量 $X$ 的可能取值为 $x_1,x_2,\dots,x_n$,我们称 $X$ 取每一个值的概率
$$P(X=x_i)=p_i\ \ \ \ \ \ \ \ \ \ i=1,2,3,\dots,n,\sum_{i=1}^n p_i=1$$
为 $X$ 的( 概率 )分布列。可以列出 $X$ 的概率分布图:
| $X$ | $x_1$ | $x_2$ | $\dots$ | $x_n$ |
|:-:|:-:|:-:|:-:|:-:|
| $P$ | $p_1$ | $p_2$ | $\dots$ | $p_n$ |
称 $X$ 服从 **两点分布 / $0-1$ 分布**,当且仅当 $n=2$,并且有:
| $X$ | $0$ | $1$ |
|:-:|:-:|:-:|
| $P$ | $p$ | $1-p$ |
- 数学期望:即加权平均数。
$$E(X)=\sum_{i=1}^nx_ip_i$$
- 方差:
$$\begin{aligned}D(X)&=\sum_{i=1}^n(x_i-E(X))^2p_i=\sum_{i=1}^n[x_i^2-2E(X)x_i+E(X)^2]p_i\\&=\sum_{i=1}^nx_i^2p_i-2E(X)\sum_{i=1}^nx_ip_i+E(X)^2\sum_{i=1}^np_i\\&=\sum_{i=1}^nx_i^2p_i-E(X)^2\end{aligned}$$
性质:
$$D(aX+b)=a^2D(X)$$
- 伯努利试验:只包含两个可能结果的试验。独立重复的做 $n$ 次 $\to n$ 重伯努利试验。在 $n$ 重伯努利试验中,设每次试验中事件 $A$ 发生的概率为 $p(0<p<1)$,用 $X$ 表示事件 $A$ 发生的次数,则 $X$ 的分布列为
$$P(X=k)=C_n^kp^k(1-p)^{n-k}\ \ \ \ \ \ \ k=0,1,2,\dots,n$$
如果随机变量 $X$ 的分布列满足上式,称随机变量 $X$ 服从**二项分布**,记作 $X\sim B(n,p)$. 由二项式定理可得
$$\sum_{k=0}^nP(X=k)=\sum_{k=0}^nC_n^kp^k(1-p)^{n-k}=[p+(1-p)]^n=1$$
例题:将一枚质地均匀硬币投掷 $10$ 次,求
$(1)$ 恰好 $5$ 次正面朝上的概率。
记 $A=$ 正面朝上,$P(A)=0.5$,记 $X$ 表示 $A$ 发生的次数,则 $X\sim B(10,0.5)$.
$$P(X=5)=C_{10}^5\times 0.5^{10}=\frac{63}{256}$$
$(2)$ 正面朝上出现的频率在 $[0.4,0.6]$ 之间的概率。
$$P(4\leq X\leq 6)=C_{10}^4\times 0.5^{10}+C_{10}^5\times 0.5^{10}+C_{10}^6\times 0.5^{10}=\frac{21}{32}$$
- 二项分布的性质:
$$\begin{aligned}E(X)&=\sum_{k=0}^nkC_n^kp^k(1-p)^{n-k}=\sum_{k=1}^nnC_{n-1}^{k-1}p^k(1-p)^{n-k}\\&=np\sum_{k=1}^nkC_{n-1}^{k-1}p^{k-1}(1-p)^{n-1-(k-1)}\ \ \ \ \ \ \ \ \ \ \ k-1=m\\&=np\sum_{m=0}^{n-1}C_{n-1}^{m}p^m(1-p)^{n-1-m}=np(p+1-p)^{n-1}=\boxed{np}\end{aligned}$$
$$\boxed{D(X)=np(1-p)}$$
- **超几何分布**:一般地,假设一批产品共 $N$ 件,其中有 $M\leq N$ 件次品。从 $N$ 件产品中随机不放回抽取 $n\leq N$ 件,用 $X$ 表示抽取的次品数,则
$$P(X=k)=\frac{C_M^kC^{n-k}_{N-M} }{C_N^n}\ \ \ \ \ \ \ \ \ \ \ k=\max\set{0,n-N+M}\sim\min\set{n,M}$$
$$\boxed{E(X)=\frac{nM}{N} \ \ \ \ \ \ \ \ \ D(X)=\frac{nM(N-M)(N-n)}{N^2(N-1)}}$$
与二项分布相比,超几何分布更集中在均值附近。
例 1:从 $50$ 名学生中随机选 $5$ 人,求甲被选中的概率。
设 $X$ 表示选出的 $5$ 名学生中含甲的人数( $0$ 或 $1$ ),
$$P(X=1)=\frac{C_1^1C_{49}^4}{C_{50}^5}=\frac{1}{10}$$
例 2:$30$ 个零件有 $3$ 个不合格。随机抽 $10$ 个有至少 $1$ 个不合格的概率 ?
设 $X$ 表示抽取的 $10$ 个零件中不合格的数量,
$$P(X=k)=\frac{C_3^kC_{27}^{10-k} }{C_{30}^{10} }\ \ \ \ \ \ k=0,1,2,3$$
$$P(X\geq 1)=1-P(X=0)=1-\frac{C_3^0C_{27}^{10} }{C_{30}^{10} }\approx 0.7192$$
### 正态分布
前提:研究连续型随机变量。
正态分布解析式:
$$\large f(x)=\frac{1}{\sigma\sqrt{2\pi} }e^{-\frac{(x-\mu)^2}{2\sigma^2} }$$
其中 $\mu\in\R,\sigma >0$ 为参数。对 $\forall x\in\R,f(x)>0$,可以用积分证明 $x$ 轴与曲线之间的区域面积为 $1$。称 $f(x)$ 为正态密度函数,图像为正态( 密度 )曲线。$X$ 服从正态分布,记为 $X\sim N(\mu,\sigma^2)$. 特别地,当 $\mu=0,\sigma=1$ 时称 $X$ 服从标准正态分布。
特点:曲线是单峰的,关于 $x=\mu$ 对称;在 $x=\mu$ 达到峰值 $\displaystyle\frac{1}{\sigma\sqrt{2\pi}}$;$\displaystyle\lim_{|x|\to\infty}f(x)=0$.
当 $\sigma$ 较小时,曲线“瘦高”,反之“矮胖”。
$$E(X)=\mu\ \ \ \ \ \ \ D(X)=\sigma^2$$
$$P(\mu-\sigma\leq X\leq \mu+\sigma)\approx 0.6827$$
$$P(\mu-1.96\sigma\leq X\leq \mu+1.96\sigma)=0.95$$
$$P(\mu-2\sigma\leq X\leq \mu+2\sigma)\approx 0.9545$$
$$P(\mu-2.58\sigma\leq X\leq \mu+2.58\sigma)=0.99$$
$$P(\mu-3\sigma\leq X\leq \mu+3\sigma)\approx 0.9973$$
$3\sigma$ 原则:服从于正态分布 $N(\mu,\sigma^2)$ 的随机变量只取 $[\mu-3\sigma,\mu+3\sigma]$ 中的值。
### 马尔科夫链
#### 一维随机游走
先来一道简单题,赌徒问题:你有本金 $A$ 元,每赌博一局,有 $50\%$ 概率赢得 $1$ 元,有 $50\%$ 概率输掉 $1$ 元,你会一直赌下去除非①没钱②达到期望 $B$ 元。记赌徒现在有 $n$ 元,求最终输光的概率 $P(n)$。上述 $A,B,n\in\N^*$.
很明显你现在有 $n$ 元进行一局后就是 $n\pm 1$ 元,两者概率相同。故 $$P(n)=\frac{1}{2}P(n-1)+\frac{1}{2}P(n+1)\implies P(n)=1-\frac{n}{B}$$
如果概率不相同,那么也很容易写出,略。( 其实就是一维随机游走 )
另外还有失足问题:一个醉鬼走在一头是悬崖( 设悬崖处于 $0$ 的位置 )的道路上,他的初始位置为 $n$,向左或向右走一步的概率都是 $\displaystyle\frac{1}{2}$,问他失足掉入悬崖的概率是多少?
答案是 $1$。因为你经过无限多次总会到达 $0$ 点。
变式:在数轴上,一个质点从 $x=0$ 位置出发随机游走,每次游走等可能地向左或向右移动 $1$ 个单位长度,求游走 $n$ 次后回到出发点的概率 $p_n$.
$\displaystyle p_{2n-1}=0,\ p_{2n}=\frac{C_{2n}^n}{4^n}$. 质点向左向右的次数必须相等。
#### 二维随机游走
【2024 山东名校联盟二模 T19】随机游走在空气中的烟雾扩散、股票市场的价格波动等动态随机现象中有重要应用,在平面直角坐标系中,粒子从原点出发,每秒向左、向右、向上或向下移动一个单位,且向四个方向移动的概率均为 $\displaystyle\frac{1}{4}$,例如在 $1s$ 末,粒子会等可能地出现在 $(1,0),(-1,0),(0,1),(0,-1)$ 四个位置。
$(2)$ 记第 $n$ 秒末粒子回到原点的概率是 $p_n$。已知 $\displaystyle\sum_{k=0}^n(C_n^k)^2=C_{2n}^n$,求 $p_3,p_4,p_{2n}$.
$(3)$ 令 $b_n=p_{2n}$,记 $S_n$ 为数列 $\set{b_n}$ 的前 $n$ 项和,若对任意实数 $M>0$,存在 $n\in\N^*$ 使得 $S_n>M$,则称粒子是常返的。已知 $\displaystyle\sqrt{2\pi n}\left(\frac{n}{e}\right)^n<n!<\left(\frac{6}{\pi}\right)^{\frac{1}{4}}\sqrt{2\pi n}\left(\frac{n}{e}\right)^n$,证明,该粒子是常返的。
解:$(2)$ 显然 $p_{2n-1}=0$. 第 $2n$ 秒末要到原点,那么必定向左向右移动 $k$ 步,向上向下移动 $n-k$ 步,有
$$p_{2n}=\sum_{k=0}^n\frac{C_{2n}^k C_{2n-k}^k C_{2n-2k}^{n-k} }{4^{2n} }=\frac{1}{4^{2n}}\sum_{k=0}^{n}\frac{(2n)!}{(k!)^2[(n-k)!]^2}=\frac{(2n)!}{4^{2n}(n!)^2}\sum_{k=0}^{n}\frac{(n!)^2}{(k!)^2[(n-k)!]^2}\\=\frac{1}{4^{2n}}C_{2n}^n\sum_{k=0}^n C_n^kC_{n}^{n-k}=\frac{(C_{2n}^n)^2}{4^{2n}}=\frac{[(2n)!]^2}{16^n(n!)^4}$$
$(3)\ \displaystyle C_{2n}^n=\frac{(2n)!}{(n!)^2}>\frac{\sqrt{4\pi n}(\frac{2n}{e})^{2n}}{[(\frac{6}{\pi})^{\frac{1}{4}}\sqrt{2\pi n}(\frac{n}{e})^n]^2}=\frac{4^n}{\sqrt{6n}}\implies b_n>\frac{1}{6n}>\frac{1}{6}\ln\frac{n+1}{n}\implies S_n>\frac{1}{6}\ln(n+1)$,这是发散的,证毕。
备注:给出的提示是 $\text{Stirling}$ 斯特林公式 $\displaystyle n!\approx\sqrt{2\pi n}\left(\frac{n}{e}\right)^n$.
#### 马尔科夫链
我们可以看到,上述问题的解决,是在一个当前的状态下,去判断前一个时刻的状态或者是后一个时刻的状态与当前状态的联系,从而找到递推式。
马尔可夫链有点类似于这样子,但它是在考虑这样的一个马尔可夫过程,过程中的**每个状态的转移只依赖于之前的 $n$ 个状态**( 动态规划的最优子结构性质?),这个过程被称为 $n$ 阶马尔可夫模型。( 其中 $n$ 是影响转移的状态数目 )
最简单的马尔科夫过程就是一阶过程,每一个状态的转移只依赖于其之前的那一个状态,这也是后面很多模型的讨论基础。
【2023 广东惠州一模】你只能吃饭或者吃面。第 $1$ 天吃饭的概率是 $\displaystyle\frac{2}{3}$,而前一天吃饭后一天继续吃饭的概率是 $\displaystyle\frac{1}{4}$,前一天吃面后一天继续吃面的概率是 $\displaystyle\frac{1}{2}$. 记第 $n$ 天吃饭概率为 $P_n$,求通项并证明 $n\geq 2$ 时 $\displaystyle P_n\leq\frac{5}{12}$.
$$P_1=\frac{2}{3}\ \ \ \ \ \ \ \ \ P_{n+1}=\frac{1}{4}P_n+\frac{1}{2}(1-P_n)=-\frac{1}{4}P_n+\frac{1}{2}\\\implies P_{n+1}-\frac{2}{5}=-\frac{1}{4}\left(P_n-\frac{2}{5}\right)\implies P_n=\frac{4}{15}\left(-\frac{1}{4}\right)^{n-1}+\frac{2}{5}$$
环状的马尔可夫:【2025 广州一模】$n(n\in\N^*,n\geq 3)$ 个人相互传球,传球规则如下:若球从甲手中传出,则甲传给乙;否则,传球者等可能地将球传给另外的 $n-1$ 个人的任何一个。第一次传球由甲手中传出,第 $k(k\in\N^*)$ 次传球后,球在甲手中的概率记为 $A_n(k)$,球在乙手中的概率记为 $B_n(k)$.
$(1)$ 求 $A_5(2),B_5(2),A_5(3),B_5(3)$;$(2)$ 求 $A_n(k)$;$(3)$ 比较 $B_n(k+1)$ 与 $\displaystyle\frac{n-2}{n-1}A_n(k)$ 的大小。
$$A_n(1)=0\ \ \ \ \ \ \ \ A_n(k+1)=\frac{1}{n-1}[1-A_n(k)]\implies A_n(k)=\frac{1}{n}\left[1-\left(-\frac{1}{n-1}\right)^{k-1}\right]$$
$$B_n(k+1)=A_n(k)+\frac{1}{n-1}[1-A_n(k)-B_n(k)]\implies B_n(k+1)=\frac{n-2}{n-1}A_n(k)+\frac{1}{n-1}-\frac{B_n(k)}{n-1}$$
$$B_n(k+1)-\frac{n-2}{n-1}A_n(k)=\frac{1}{n-1}[1-B_n(k)]\geq 0$$
当且仅当 $k=1$ 时取等。这是个比较难算的题。更难的题目见 [here](https://zhuanlan.zhihu.com/p/1695634769)
---
一个平面的俯视图为一个 $3\times 3$ 的方格表。初始时在中心位置有一个电子瓢虫,每过一秒钟随机向上下左右移动一个单位,跌落平台就会死亡。那么在 $2023$ 秒后,仍然存活的概率是 ?
设第 $n$ 秒后瓢虫在中心的概率是 $z_n$,在角的概率是 $j_n$,在边中间的概率是 $b_n$,于是
$$z_1=0,j_1=0,b_1=1\ \ \ \ z_2=\frac{1}{4},j_2=\frac{1}{2},b_2=0$$
$$\begin{cases}\displaystyle z_n=\frac{1}{4}b_{n-1}\\\displaystyle j_n=\frac{1}{2}b_{n-1} \\\displaystyle b_n=z_{n-1}+\frac{1}{2}j_{n-1}\end{cases}\implies b_{n+1}=z_n+\frac{1}{2}j_n=\frac{1}{2}b_{n-1}\implies b_{2023}=\frac{1}{2^{1011}},b_{2022}=0$$
显然答案为 $\displaystyle\frac{1}{2^{1011}}$.
<!--
连续抛 $10$ 枚硬币,出现连续 $5$ 次及以上正面朝上的概率为 ?
$\displaystyle\text{A}. \frac{15}{128}\ \ \text{B}. \frac{29}{256}\ \ \text{C}. \frac{7}{64}\ \ \text{D}. \frac{5}{32}$
正难则反,考虑不出现连续 $5$ 次正面朝上的情况。定义状态 `dp[i][j]` 表示前 $i$ 次抛硬币中,最后 $j$ 次都是正面,并且从未出现过连续 $5$ 次正面的情况。其中 $j\in\set{0,1,2,3,4}$。我们有
- $dp[i][0]=\displaystyle\sum_{j=0}^4 dp[i-1][j]$ 第 $i$ 次抛反面,连续正面次数归零。
- $j\geq 1$ 时,$dp[i][j]=dp[i-1][j-1]$ 第 $i$ 次抛正面,连续正面次数 $+1$。
初始条件:$dp[0][0]=1$。好了我们启动计算机计算得到 $\displaystyle\sum_{j=0}^4 dp[10][j]=912$,于是答案为 $\displaystyle1-\frac{912}{2^{10}}=\frac{7}{64}$ -->
---
【2024 武汉部分学校调研】$n$ 个盒子 $k$ 个球,$n\geq 2,n\in\N^*$ 且 $2\leq k\leq n,k\in\N$. 规则如下:每个盒子最多放一个球。先将 $1$ 号球随机放在任意一个盒子中,剩下的球从小到大依次放置。若球的编号对应的盒子为空,则放进去;否则随机挑一个空盒子放进去。记 $k$ 号球能放入 $k$ 号盒子的概率为 $P(n,k)$.
$(1)$ 求 $P(3,3)$;$(2)$ 当 $n\geq 3$ 时,求 $P(n,3)$;$(3)$ 求 $P(n,k)$.
答案:$\displaystyle (1)\ \frac{1}{2}\ \ (2)\ \frac{n-2}{n-1}\ \ (3)\ \frac{n-k+1}{n-k+2}$.
解析:$(3)$ 先考虑 $1$ 号球放在 $1$ 号或 $k+1$ 到 $n$ 号盒子里,这部分概率为 $\displaystyle\frac{n-k+1}{n}$.
再考虑 $1$ 号球放 $j\in[2,k-1]$ 号盒子,概率为 $\displaystyle\frac{1}{n}$,此时 $2$ 号到 $j-1$ 号球正常放,剩下 $j,j+1,j+2,\dots,k$ 号球放 $1,j+1,j+2,\dots,n$ 的空盒,$k$ 号球能放入 $k$ 号盒子的概率相当于 $P(n-j+1,k-j+1)$.
$$P(n,k)=\frac{n-k+1}{n}+\frac{1}{n}\sum_{j=2}^{k-1}P(n-j+1,k-j+1)$$
$$\implies nP(n,k)=n-k+1+\sum_{j=2}^{k-1}P(n-j+1,k-j+1)$$
$$(n-1)P(n-1,k)=n-k+\sum_{j=2}^{k-1}P(n-j,k-j+1)$$
相减得 $\displaystyle P(n,k)=P(n-1,k-1)=\dots=P(n-k+2,2)=\frac{n-k+1}{n-k+2}$.
### 其他好题
甲、乙两人玩游戏。规则如下:奇数局甲赢的概率是 $\displaystyle\frac{3}{4}$,偶数局乙赢的概率是 $\displaystyle\frac{3}{4}$. 没有平局。规定:当一个人赢的局数比另一个人赢的局数多 $2$ 次时游戏结束。求游戏结束时甲、乙两人玩的游戏局数的数学期望。
设玩 $X$ 局,则期望为 $E(X)$。显然 $\displaystyle P(X=2)=\frac{3}{4}\times\frac{1}{4}\times 2=\frac{3}{8}.\ \text{}$否则前两局的比分为 $1:1$,相当于 $0:0$ 的情况,只不过多比了 $2$ 次。所以 $$E(X)=\frac{3}{8}\times 2+\left(1-\frac{3}{8}\right)\times[E(X)+2]\implies E(X)=\frac{16}{3}$$
# 线性规划
### 例题 1
$$\begin{cases}5x-11y \geq -22 \\ 2x+3y \geq 9 \\ 2x \leq 11\end{cases}$$
$z = 10x + 10y, \max{z} = $ ?
### 基本概念
1. 约束条件:变量 $x,y,\dots$ 满足的一组条件,上述二元一次不等式组就是对 $x,y$ 的约束条件。
2. 线性约束条件:由变量 $x,y,\dots$ 的一次不等式 / 方程组成的不等式组就称为线性约束条件,如上述二元一次不等式。
3. 目标函数:欲求最大值或最小值所涉及的变量 $x,y,\dots$ 的解析式,如上述 $z$.
4. 线性目标函数:目标函数关于变量 $x,y,\dots$ 的一次解析式,如上述 $z$.
5. 线性规划问题:在线性约束条件下求线性目标函数的问题。
6. 可行解:满足线性约束条件的解 $(x,y)$.
7. 可行域:由所有可行解组成的集合。
8. 最优解:使目标函数取得 $\max$ 或 $\min$ 的可行解。
### 解法
1. 画图,数形结合。
$$\begin{cases}5x-11y \geq -22 & \displaystyle \implies y \leq \frac{5}{11}x + \frac{1}{2} & \implies & \displaystyle y = \frac{5}{11}x + \frac{1}{2}\ 图像的下边 \\ 2x+3y \geq 9 & \displaystyle \implies y \geq -\frac{2}{3}x + 3 & \implies & \displaystyle y = -\frac{2}{3}x + 3\ 图像的上边 \\ 2x \leq 11 & \displaystyle \implies x \leq \frac{11}{2} & \implies & \displaystyle x=\frac{11}{2}\ 图像的左边 \end{cases}$$
在平面直角坐标系上画出对应的平面区域 ( 可行域 ),再把目标函数 $z=ax+by$ 变形为 $\displaystyle y=-\frac{a}{b}x + \frac{z}{b}$,$\\$ 所以求 $z$ 的最值可看成是求直线 $\displaystyle y=-\frac{a}{b}x + \frac{z}{b}$ 在 $y$ 轴上截距的最值。以这题为例,$\displaystyle z=10x+10y \implies y= -x + \frac{z}{10}$ 容易证明,当 $z=85$ 时 $y$ 轴上截距取最值,所以 $\max{z}=85.$
2. 仔细观察,可以发现最优解非常容易出现在可行域构成的**多面体的顶点**处。
### 例题 2
$$\begin{cases}y \geq x \\ x + y \leq 2 \\ x \geq a\end{cases}$$
$(2x+y)_{\mathrm{max}}=4(2x+y)_{\mathrm{min}},\ a= $ ?
- 求 $(2x+y)_{\mathrm{min}}$:$x_{\min}=a \implies y_{\min}=a \implies (2x+y)_{\mathrm{min}}=3a$
- 求 $(2x+y)_{\mathrm{max}}$:$\begin{cases}x-y\leq 0 \\ x+y\leq 2\end{cases}\xRightarrow{\mathrm{Add\ }} x\leq 1\implies y\leq 1\implies (2x+y)_{\mathrm{max}}=3$
- $\displaystyle 3=4\times 3a\implies a=\frac{1}{4}$
### 例题 3( 2024 九省联考 T14 )
$$\begin{cases} 0<a<b<c<1 \\ b\geq 2a \ \ \ \mathrm{or}\ \ \ a+b\leq 1 \end{cases}$$
$\max{\set{b-a,c-b,1-c}}$ 的最小值 $=$ ?
- 注意到 $c$ 的约束条件是最少的,首先考虑消去它,得到
$$\max{\set{b-a,c-b,1-c}}\geq\max{\set{b-a,\frac{1-b}{2}}}$$
$\ \ \ \ \ \ \text{}$ 当且仅当 $\displaystyle c=\frac{1+b}{2}$ 取等,消去 $c$ 后把 $a$ 看作 $x$,把 $b$ 看作 $y$ 得:
$$\begin{cases}0<x \\ x<y \\ y<1 \\ y\geq 2x\ \ \ \mathrm{or}\ \ \ x+y\leq 1\end{cases}$$
- 作出可行域:$\mathrm{and}$ 连接的区域之间取交,$\mathrm{or}$ 连接的区域之间取并。阴影部分即为可行域。
$\ \ \ \ \ \ \text{}$ 图中 $y\geq 2x\ \ \ x+y\leq 1$ 两条解析式用红色标出。

- 回到题目,要求 $\displaystyle M=\max{\set{y-x,\frac{1-y}{2}}}$,我们需要知道何时 $M=y-x$,何时 $\displaystyle M=\frac{1-y}{2}$.
$\ \ \ \ \ \ \text{}$ 直接列方程 $\displaystyle y-x=\frac{1-y}{2}$ 可以得到 $\displaystyle y=\frac{2}{3}x+\frac{1}{3}$,在图中作出这条直线,得到:
- 因为最终要求的是 $M$ 的最小值,所以对蓝色区域而言,$y$ 尽量小,$x$ 尽量大,根据例题 1 的经验,这样的极值点通常出现在多边形的顶点处,经过比较后 $P$ 点是极值点,此时 $M=0.2$. 对绿色区域而言,只需满足 $y$ 尽量大,显然,$P$ 点也是极值点。
- 综上所述,$\max{\set{b-a,c-b,1-c}}$ 的最小值 $\displaystyle=\frac{1}{5}$.
# 数论
## 基本技巧
- 若 $n$ 是正整数,则
$$\red{\boxed{x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+\dots+xy^{n-2}+y^{n-1})}}$$
- 若 $n$ 是正 **$\red{奇数}$**,则
$$\red{\boxed{x^n+y^n=(x+y)(x^{n-1}-x^{n-2}y+\dots-xy^{n-2}+y^{n-1})}}$$
例 1:证明 $10^{201}+1$ 能被 $1001$ 整除。
显然 $10^{201}+1=(10^3)^{67}+1^{67}=1001[(10^3)^{66}-(10^3)^{65}+\dots-10^3+1]$.
---
例 2:设 $m>n\geq 0$,证明:$(2^{2^n}+1)|(2^{2^m}-1)$.
显然 $2^{2^m}-1=(2^{2^{n+1}}-1)[(2^{2^{n+1}})^{2^{m-n-1}-1}+\dots+2^{2^{n+1}}+1]$,故 $(2^{2^{n+1}}-1)|(2^{2^m}-1)$。又 $2^{2^{n+1}}-1=(2^{2^n}+1)(2^{2^n}-1)$,故原命题得证。
---
例 3:设 $k\geq 1$ 是一个奇数,证明:$\forall n\in\N^*,(n+2)\nmid (1^k+2^k+\dots+n^k)$.
$n=1$ 显然成立,又 $2RHS=2+(2^k+n^k)+(3^k+(n-1)^k)+\dots+(n^k+2^k)$,显然 $\forall i\geq 2,(n+2)|(i^k+(n-i+2)^k)$。故 $2RHS\ \mathrm{mod}\ (n+2)=2$.
---
练 1:求满足 $(n+11)|(n^2+9n-2)$ 的正整数 $n$.
练 2:整数 $a,b,c,d$ 满足 $ad-bc>1$,证明 $a,b,c,d$ 中至少有一个数不被 $ad-bc$ 整除。
## 因数
### 整除
若 $b$ 能整除 $a$,则记为 $a\mid b$,如 $2\mid 12$. 若 $b$ 不能整除 $a$,则记为 $a\nmid b$,如 $5\nmid 12$.
若 $a\nmid b$,则 $b\div a$ 存在余数 $r$ 且 $0<r<a$,记 $r=a\ \mathrm{mod}\ b$. 例如,$3\ \mathrm{mod}\ 2=1$.
整除具有以下性质:
1. 若 $a\mid b$ 且 $a\mid c$,则 $\forall x,y$,有 $a\mid xb+yc$.
2. 若 $a\mid b$ 且 $b\mid c$,则 $a\mid c$.
3. 若 $a\mid b$ 且 $b\mid a$,则 $a=\pm b$.
4. 设 $m\neq 0$,则 $a\mid b$,当且仅当 $ma\mid mb$.
### 最大公因数与最小公倍数
设 $a,b$ 是两个不为 $0$ 的整数,能使 $d\mid a$ 和 $d\mid b$ 成立的最大整数 $d$,称为 $a,b$ 的最大公因数,记作 $\gcd(a,b)$.
设 $a,b$ 是两个不为 $0$ 的整数,能使 $a\mid d$ 和 $b\mid d$ 成立的最小整数 $d$,称为 $a,b$ 的最小公倍数,记作 $\mathrm{lcm}(a,b)$.
- $\forall a,b\in\N,\ \gcd(a,b)\cdot\mathrm{lcm}(a,b)=ab$
证明:设 $\displaystyle d=\gcd(a,b),a_0=\frac{a}{d},b_0=\frac{b}{d}$. 根据最大公因数的定义,有 $\gcd(a_0,b_0)=1$。$\\\ \ \ \ \ \ \ \ \ \text{}$ 再根据最小公倍数的定义,有 $\mathrm{lcm}(a,b)=a_0\cdot b_0$. $\\\ \ \ \ \ \ \ \ \ \text{}$ 于是 $\displaystyle\mathrm{lcm}(a,b)=\mathrm{lcm}(a_0\cdot d,b_0\cdot d)=\mathrm{lcm}(a_0,b_0)\cdot d=a_0\cdot b_0\cdot d=\frac{a\cdot b}{d}$,原命题得证。
- 九章算术 更相减损术: $\gcd(a,b)=\gcd(b,a-b)=\gcd(a,a-b),\gcd(2a,2b)=2\gcd(a,b)$.
证明:$d\mid a,d\mid b\implies d\mid(a-b)$.
- 欧几里得算法:$\forall a,b\in\N,b\neq 0,\gcd(a,b)=\gcd(b,a\ \mathrm{mod}\ b)$.
证明:分类讨论。
1. 若 $a<b$,则有 $\gcd(b,a\ \mathrm{mod}\ b)=\gcd(b,a)=\gcd(a,b)$.
2. 若 $a\geq b$,不妨设 $a=q\cdot b+r\ (0\leq r<b)$。显然 $r=a\ \mathrm{mod}\ b$. 对于 $a,b$ 的任意公因数 $d$,$\\$ 因为 $d\mid a,d\mid q\cdot b$,故 $d\mid (a-q\cdot b)$,即 $d\mid r$. 因此 $d$ 也是 $b,r$ 的公因数,反之亦成立。$\\$ 故 $a,b$ 的公因数集合与 $b,a\ \mathrm{mod}\ b$ 的公因数集合相同。于是它们的最大公因数也相等。
## 裴蜀定理
设 $a,b\in\Z,ab\neq 0$,则 $\exist x,y\in\Z$ 使 $ax+by=\gcd(a,b)=a(x+bu)+b(y-au)$
由上易推出两个**整数 $a,b$ 互素的充分必要条件是 $\exist x,y\in\Z$ 使得 $ax+by=1$。**
比如要证明 $21n+4$ 与 $14n+3$ 互素,知道 $3(14n+3)-2(21n+4)=1$ 即可。
例 1:证明 $n!+1$ 与 $(n+1)!+1$ 互素。
有 $(n+1)(n!+1)-[(n+1)!+1]=n$,于是 $[d=\gcd(n!+1,(n+1)!+1)]|n$,又因为 $d|n!$,结合 $d|(n!+1)$ 得到 $d=1$,原命题得证。
---
例 2:记费马数 $F_k=2^{2^k}+1,k\geq 0$,证明若 $m\neq n$ 则 $\gcd(F_m,F_n)=1$.
设 $m>n$,只要利用 $F_n|(F_m-2)$ 证明 $\exist x\in\Z$ 使得 $F_m+xF_n=2$【基本技巧例 2】
设 $[d=\gcd(F_m,F_n)]|2$. $F_n$ 显然为奇数故 $d=1$. 因此**费马数两两互素。**
---
例 3:设 $a>1,m,n>0$,证明 $\boxed{\gcd(a^m-1,a^n-1)=a^{\gcd(m,n)}-1}$
令 $D=\gcd(a^m-1,a^n-1)$,只要证明 $[a^{\gcd(m,n)}-1]|D$ 及 $D|[a^{\gcd(m,n)}-1]$ 即可。
显然 $[a^{\gcd(m,n)}-1]|(a^m-1)$ 和 $[a^{\gcd(m,n)}-1]|(a^n-1)$,可以证明 $[a^{\gcd(m,n)}-1]|D$.
设 $d=\gcd(m,n)$,可选 $u,v>0$,使 $mu-nv=d$. 因此 $D|(a^m-1),D|(a^{mu}-1)$,扩展开来 $D|(a^{mu}-a^{nv})=a^{nv}(a^d-1)$,故 $D|(a^d-1)$. 综合上述原命题得证。
---
例 4:设 $m,n>0,mn|(m^2+n^2)$,证明 $m=n$.
设 $\gcd(m,n)=d,m=m_1d,n=n_1d,\gcd(m_1,n_1)=1$①. 已知化为 $m_1n_1|(m_1^2+n_1^2)$,从而 $m_1|n_1^2,n_1|m_1^2$. 结合①可得 $m_1=n_1=1,m=n$.
---
例 5:设 $k$ 为正奇数,证明 $\displaystyle\sum_{i=1}^ni$ 整除 $\displaystyle\sum_{i=1}^ni^k$.
等价于证明 $n|2\displaystyle\sum_{i=1}^ni^k$ 和 $(n+1)|2\displaystyle\sum_{i=1}^ni^k$,显然
$$\begin{aligned}2\sum_{i=1}^ni^k&=[1^k+(n-1)^k]+[2^k+(n-2)^k]+\dots+[(n-1)^k+1^k]+2n^k\\&=[1^k+n^k]+[2^k+(n-1)^k]+\dots+[n^k+1^k]\end{aligned}$$
是 $n$ 和 $n+1$ 的倍数。
由上可知,为了证明 $b|a$,只需将 $b$ 分解成若干个两两互素的整数 $b_1,b_2,\dots,b_n$ 之积,证明 $b_i|a$ 即可。
## 质数
- 定义:一个正整数无法被除了 $1$ 和它自身之外的任何自然数整除,则成为质数,否则为合数。
- 数量:对于一个足够大的整数 $N$,不超过 $N$ 的质数有 $\displaystyle\pi(x)\approx\frac{N}{\ln N}$ 个,所以第 $n$ 个质数约为 $n\ln n$.
- 判定:试除法,若 $N$ 为合数,则存在一个能整除 $N$ 的数 $T$ 且 $2 \leq T \leq \sqrt{N}$.
- 算数基本定理:$N = p_1^{c_1}p_2^{c_2}\dots p_n^{c_n}$,$N$ 的正约数个数 $=\red{\boxed{\displaystyle\prod_{i=1}^{n}(c_i+1)}}$,$N$ 的所有正约数的和 $=\displaystyle\prod_{i=1}^{n}(\displaystyle\sum_{j=0}^{c_i}(p_i)^j)=\red{\boxed{\prod_{i=1}^n\frac{p_i^{c_i+1}-1}{p_i-1}}}$.
一个正整数 $N$ 的约数个数上界为 $2\sqrt{N}$,$1$ ~ $N$ 每个数的约数个数的总和大约为 $N\log N$.
- 设 $b|ac$,若 $\gcd(b,c)=1$,则 $b|a$.
- 设 $a,b\in\N^*$ 且 $a,b$ 之积是一个整数的 $k(k\geq 2)$ 次幂,若 $\gcd(a,b)=1$,则 $a,b$ 都是整数的 $k$ 次幂。一般地,设正整数 $a,b,\dots,c$ 之积是一个整数的 $k$ 次幂,且 $a,b,\dots,c$ 两两互质,则 $a,b,\dots,c$ 都是整数的 $k$ 次幂。
- 对任意正整数 $m$ 及质数 $p$,记 $p^c\Vert m$ 表示 $p^c|m$ 但 $p^{c+1}\nmid m$,即 $p^c$ 是 $m$ 的标准分解中出现的 $p$ 的幂。
- 设 $n>1,p$ 为质数,$p^{c_p}\Vert n!$,则 $c_p=\displaystyle\sum_{l=1}^{+\infty}\lfloor\frac{n}{p^l}\rfloor$
例 1:证明无穷数列 $10001,100010001,\dots$ 中无质数。
记 $\displaystyle a_n=1+10^4+\dots+10^{4(n-1)}=\frac{10^{4n}-1}{10^4-1}$,接下来分 $n$ 为奇偶讨论即可。
$$a_{2k}=\frac{10^{8k}-1}{10^4-1}=\frac{10^{8k}-1}{10^8-1}\cdot\frac{10^8-1}{10^4-1}$$
$$a_{2k+1}=\frac{10^{4(2k+1)}-1}{10^4-1}=\frac{10^{2(2k+1)}-1}{10^2-1}\cdot\frac{10^{2(2k+1)}+1}{10^2+1}$$
例 2:证明 $\forall n\in\N^*,n>1,n^4+4^n$ 不是质数。
$n$ 为偶数显然。$n$ 为奇数时,设 $n=2k+1$,
$$\begin{aligned}n^4+4^n&=n^4+4\cdot 4^{2k}=n^4+4\cdot (2k)^4=n^4+4n^2\cdot(2^k)^2+4\cdot(2k)^4-4n^2\cdot(2^k)^2\\&=(n^2+2\cdot 2^{2k})^2-(2n\cdot 2^k)^2=(n^2+2^{k+1}n+2^{2k+1})(n^2-2^{k+1}n+2^{2k+1})\end{aligned}$$
即把 $4^n$ 看成 $4y^4$,有 $\red{\boxed{x^4+4y^4=(x^2+2y^2+2xy)(x^2+2y^2-2xy)}}$
练 1:设 $a,b,c,d\in\N^*,ab=cd$,证明 $a+b+c+d$ 不是质数。
例 3:证明:若 $a,b\in\Z,2a^2+a=3b^2+b$,则 $a-b$ 和 $2a+2b+1$ 都为完全平方数。
已知化为 $(a-b)(2a+2b+1)=b^2$,设 $d=\gcd(a-b,2a+2b+1)$,若 $d>1$,则 $d$ 有质因子 $p$,$p|b^2\implies p|b$,$p|(a-b)\implies p|a\implies p|1$,这不可能,因此 $d=1$. 因为 $b^2$ 是完全平方数,由此可得 $|a-b|,|2a+2b+1|$ 也是完全平方。
只要证 $a-b$ 和 $2a+2b+1$ 不能同时 $<0$ 即可。设 $a-b<0$,则 $b-a=r^2$. 显然 $r|b,r|a$,令 $b=b_1r,a=a_1r$,代入题目 $a_1^2+6a_1r+3r^2+1=0$,得 $a_1=-3r\pm\sqrt{6r^2-1}$,显然 $6r^2-1$ 应为完全平方数,而 $6r^2-1\equiv 2\ (\mathrm{mod}\ 3)$,矛盾,原命题得证。
## 不定方程
例 1:证明两个连续正整数之积不能是完全平方或完全立方。
反证法,即设 $x(x+1)=y^2$ 有解,则 $(2x+1)^2=4y^2+1$,分解为
$$(2x+1+2y)(2x+1-2y)=1\implies\begin{cases}2x+1+2y=1\\2x+1-2y=1\end{cases}\implies x=y=0$$
显然不可能。类似的,对于完全立方,由于 $x$ 和 $x+1$ 互质,可得它们都是立方数。设 $x=u^3,x+1=v^3,y=uv,v^3-u^3=1=(v-u)(v^2+uv+u^2)$,显然不可能。
类似的,可证明连续两个正整数之积不能是整数的 $k(k\geq 2)$ 次幂。
练 1:设 $k\in\N^*,k\geq 2$,证明:连续三个正整数之积不能是整数的 $k$ 次幂。
提示:$x(x^2-1)=y^k\implies a^kb^k=(ab)^k,1=a^{2k}-b^k=(a^2)^k-b^k$,导出矛盾。
---
例 2:证明方程 $y^2+y=x+x^2+x^3$ 没有 $x\neq 0$ 的整数解。
转化为 $(y-x)(y+x+1)=x^3$,可以证明 $\gcd(y-x,y+x+1)=1$,设 $y-x=a^3,y+x+1=b^3,x=ab$,可得 $b^3-a^3=(b-a)(b^2+ab+a^2)=2ab+1③$,证明该方程无解即可。$ab>0$ 时,$b-a\geq 1$,③的左边 $\geq 3ab>$ 右边;$ab<0$ 时,③的左边的绝对值 $\geq 2(a^2+b^2-|ab|)>2|ab|>$ ③的右边的绝对值。因此原命题成立。
练 2:求方程 $(x^2-y^2)^2=1+16y$ 的所有整数解。
提示:$y\geq 0,|x|\geq$ 或 $\leq y+1$,均可得出 $(x^2-y^2)^2\geq(2y-1)^2$,得 $(2y-1)^2\leq 1+16y$,答案 $(x,y)=(\pm 1,0),(\pm 4,3)(\pm4,5)$.
---
例 3:设 $x,y,z\in\N^*,2x^x=y^y+z^z$,证明 $x=y=z$.
$$(x+1)^{x+1}>x^{x+1}+(x+1)x^x>2x^x\implies y,z\leq x$$
反之,设 $y\geq x+1$,则 $y^y+z^z>(x+1)^{x+1}>2x^x$,矛盾。而 $y^y+z^z\leq x^x+x^x=2x^x$,所以 $x=y=z$.
## 欧拉函数
$1$ ~ $N$ 中与 $N$ 互质的数的个数被称为欧拉函数,记为 $\varphi(N)$. 用数学符号表示即为 $\varphi(N)=\displaystyle\sum_{i=1}^{N}[\gcd(i,N)=1]$.
若 $N = p_1^{c_1}p_2^{c_2}\dots p_n^{c_n}$,则 $\displaystyle\varphi(N)=N\times\frac{p_1-1}{p_1}\times\frac{p_2-1}{p_2}\times\dots\times\frac{p_n-1}{p_n}=N\cdot\displaystyle\prod_{质数p|N}\left(1-\frac{1}{p}\right)$
证明:设 $p,q$ 为 $N$ 的不同质因子,$1$ ~ $N$ 中 $p$ 的倍数有 $\displaystyle \frac{N}{p}$ 个,$q$ 的倍数有 $\displaystyle \frac{N}{q}$ 个。若把 $\displaystyle \frac{N}{p}+\frac{N}{q}$ 个数去掉,则 $\displaystyle\frac{N}{pq}$ 被计算了 $2$ 次( 容斥原理 )。因此, $1$ ~ $N$ 中不与 $N$ 含有相同质因子的 $p$ 或 $q$ 数量为 $\displaystyle N-\frac{N}{p}-\frac{N}{q}+\frac{N}{pq}=N\left(1-\frac{1}{p}\right)\left(1-\frac{1}{q}\right)$,对 $N$ 的全部质因子继续容斥即可得到公式。
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ | $13$ | $14$ | $15$ |
| :----------: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\varphi(n)$ | $1$ | $1$ | $2$ | $2$ | $4$ | $2$ | $6$ | $4$ | $6$ | $4$ | $10$ | $4$ | $12$ | $6$ | $8$ |
欧拉函数的性质:
1. $\forall n>1$,$1$ ~ $n$ 中与 $n$ 互质的数的和为 $\displaystyle\frac{n\times\varphi(n)}{2}$.
2. 若 $a,b$ 互质,则 $\varphi(ab)=\varphi(a)\varphi(b)$.
3. 设 $p$ 为质数,$\varphi(p)=p-1$.
4. 设 $p$ 为质数,$k\in\N^*,\varphi(p^k)=p^{k-1}\times(p-1)=p^k-p^{k-1}$.
5. 设 $p$ 为质数,若 $p\mid n$ 且 $p^2\mid n$,则 $\displaystyle\varphi(n)=\varphi\left(\frac{n}{p}\right)\times p$.
6. 设 $p$ 为质数,若 $p\mid n$ 但 $p^2\nmid n$,则 $\displaystyle\varphi(n)=\varphi\left(\frac{n}{p}\right)\times (p-1)$.
7. 若 $n$ 为奇数,则 $\varphi(2n)=\varphi(n)$.
8. $\forall n\geq 3,\ n\in\N^*,\ 2\mid\varphi(n)$.
9. 欧拉反演:$\displaystyle\sum_{d\mid n}\varphi(d)=n$.
证明:
1. 因为 $\gcd(n,x)=\gcd(n,n-x)$,所以与 $n$ 不互质的数 $x,n-x$ 成对出现,平均值为 $\displaystyle\frac{n}{2}$. $\\$ 因此与 $n$ 互质的数的平均值也是 $\displaystyle\frac{n}{2}$,进而得到性质 1。
2. 根据欧拉函数的计算式可直接获得性质 2。
3. 根据欧拉函数的定义可直接获得性质 3。
4. 从 $1$ ~ $p^{k}$ 中的所有数,除了 $p^{k-1}$ 个 $p$ 的倍数外都与 $p^k$ 互素。
5. 若 $p\mid n$ 且 $p^2\mid n$,则 $\displaystyle n,\frac{n}{p}$ 包含相同的质因子,只是 $p$ 的指数不同。$\\$ 按照欧拉函数的计算公式,$\displaystyle \frac{\varphi(n)}{\varphi(\frac{n}{p})}=\frac{n}{\frac{n}{p}}=p$,得到性质 5。
6. 若 $p\mid n$ 且 $p^2\mid n$,则 $\displaystyle n,\frac{n}{p}$ 互质。因为 $\displaystyle\varphi(n)=\varphi\left(\frac{n}{p}\right)\varphi(p)$,而 $\varphi(p)=p-1$,得到性质 6。
7. $\forall m<2n,m\in\N^*$,若 $2\mid m$,则 $\gcd(m,2n)\neq 1$,也就是对欧拉函数的值没有贡献;$\\$若 $2\nmid m$,则 $\gcd(m,2n)=1$,欧拉函数的值也就与 $2n$ 中的偶质因子无关。
8. $n\geq 3$ 时,与 $n$ 互质的数不可能为 $\displaystyle\frac{n}{2}\implies\forall x<n,\gcd(x,n)=\gcd(n-x,n)$,也就是存在一一对应关系。
9. 设 $f(n)=\displaystyle\sum_{d\mid n}\varphi(d)$,利用 $\varphi$ 是积性函数,得到:$\\$若 $n,m$ 互质,则 $f(nm)=\displaystyle\sum_{d\mid nm}\varphi(d)=\displaystyle\sum_{d\mid n}\varphi(d)\cdot\displaystyle\sum_{d\mid m}\varphi(d)=f(n)f(m)$,即 $f(n)$ 是积性函数。$\\$ 对于单个质因子有:$\begin{aligned}f(p^m)&=\displaystyle\sum_{d\mid p^m}\varphi(d)=\displaystyle\sum_{i=0}^{m}\varphi(p^i)=\varphi(1)+\varphi(p)+\varphi(p^2)+\varphi(p^3)+\dots+\varphi(p^m)\\&= 1+(p-1)+(p-1)p+(p-1)p^2+\dots+(p-1)p^{m-1}\\&=1+(p-1)+(p^2-p)+(p^3-p^2)+\dots+(p^m-p^{m-1})=p^m\end{aligned} \\$ 所以 $f(n)=\displaystyle\prod_{i=1}^{m}f(p_i^{c_i})=\displaystyle\prod_{i=1}^{m}p_i^{c_i}=n$
### 积性函数与完全积性函数
若函数 $f(x)$ 满足 $f(1)=1$ 且 $\forall x,y\in\N^{*},\gcd(x,y)=1$ 都有 $f(xy)=f(x)f(y)$,则 $f(x)$ 是积性函数。
若函数 $f(x)$ 满足 $f(1)=1$ 且 $\forall x,y\in\N^{*}$ 都有 $f(xy)=f(x)f(y)$,则 $f(x)$ 是完全积性函数。
性质:
1. 若 $f(x)$ 和 $g(x)$ 均为积性函数,则以下函数也为积性函数:
$$\begin{aligned}h(x)&=f(x^p) \\ h(x)&=f^p(x) \\ h(x)&=f(x)g(x) \\ h(x)&=\displaystyle\sum_{d\mid x}f(d)g\left(\frac{x}{d}\right)\end{aligned}$$
2. 设 $x=\displaystyle\prod p_i^{c_i}$,
若 $f(x)$ 为积性函数,则 $f(x)=\displaystyle\prod f(p_i^{c_i})$。
若 $f(x)$ 为完全积性函数,则 $f(x)=\displaystyle\prod f^{c_i}(p_i)$。
例子:
积性函数:$\varphi(n),\sigma _k(n)=\displaystyle\sum_{d\mid n}d^k,\sigma _0(n)$ 通常简记为 $d(n)$ 或 $\tau(n)$,$\sigma _1(n)$ 通常简记为 $\sigma(n)$。
完全积性函数:$\varepsilon(n)=[n=1],\text{id}_k(n)=n^k,\text{id}_1(n)$ 通常简记为 $\text{id}(n),f(n)=1$.
## 同余
- 平方数 $\mathrm{mod}\ 4\equiv 0$ 或 $1,\mathrm{mod}\ 8\equiv0$ 或 $1$ 或 $4,\mathrm{mod}\ 3\equiv 0$ 或 $1,\mathrm{mod}\ 5\equiv0$ 或 $\pm 1$.
- 立方数 $\mathrm{mod}\ 9\equiv 0$ 或 $\pm 1$.
- 四次幂 $\mathrm{mod}\ 16\equiv 0$ 或 $1$.
例如可证明 $a,b,c,d\in\N^*,a^{4b+d}-a^{4c+d}$ 能被 $240=2^4\times 3\times 5$ 整除。
例 1:设 $a,b,c\in\Z,a+b+c=0,d=a^{1999}+b^{1999}+c^{1999}$,证明 $d$ 可被 $6$ 整除。
$$u^{1999}\equiv u(\mathrm{mod}\ 2)\implies d\equiv a+b+c\equiv 0(\mathrm{mod}\ 2)\implies2|d$$
$$u^3\equiv u(\mathrm{mod}\ 3)\implies u^{1999}\equiv u\cdot u^{1998}\equiv u\cdot u^{666}\equiv u\cdot u^{222}\equiv u^{75}\equiv u^{25}\equiv u^9\equiv u(\mathrm{mod}\ 3)$$
<!-- 注意 $u^3\equiv u(\mathrm{mod}\ 3)$ 是费马小定理的特殊情形。 -->
练 1:设 $x,y,z\in\Z,(x-y)(y-z)(z-x)=x+y+z$,证明 $27|(x+y+z)$.
只要证明 $x,y,z$ 两两模 $3$ 同余即可。
练 2:证明 $11,111,1111,\dots$ 不是完全平方数。只要知道 $11\ \mathrm{mod}\ 4\neq 0$ 即可。
---
例 2:数列 $\set{x_n}$ 为 $1,3,5,11,\dots$,满足 $x_{n+1}=x_n+2x_{n-1}$.
数列 $\set{y_n}$ 为 $7,17,55,161,\dots$,满足 $y_{n+1}=2y_n+3y_{n-1}$. 证明:两个数列无相同项。
考虑以 $8$ 为模,因为 $x_2\equiv 3,x_3\equiv 5$. 若 $x_{n-1}\equiv 3,x_n\equiv 5$,则 $x_{n+1}\equiv 3,x_{n+2}\equiv 5$.
显然 $\set{x_n}$ 是模 $8$ 后的周期数列,同理 $\set{y_n}$ 也是( $7,1,7,1,\dots$ ),于是命题得证。
### 费马小定理与欧拉定理
若整数 $a$ 和整数 $b$ 除以正整数 $m$ 的余数相等,则称 $a,b$ 模 $m$ 同余,记为 $a\equiv b\ (\mathrm{mod}\ m)$.
并且注意到 $\displaystyle k\ \mathrm{mod}\ i=k-\left\lfloor\frac{k}{i}\right\rfloor\cdot i$,且同余满足同加性、同乘性、同幂性,但不满足同除性。
对于 $\forall a \in [0, m - 1]$,集合 $\set{a+km\ (k\in\Z)}$ 的所有数模 $m$ 同余,余数都是 $a$. 该集合称为一个模 $m$ 的同余类,简记为 $\overline{a}$.
模 $m$ 的同余类一共有 $m$ 个,分别为 $\overline{0},\overline{1},\overline{2},\dots,\overline{m-1}$. 它们构成 $m$ 的完全剩余系。
$1$ ~ $m$ 中与 $m$ 互质的数代表的同余类共有 $\varphi(m)$ 个,它们构成 $m$ 的简化剩余系。$\\$例如,模 $10$ 的简化剩余系为 $\set{\overline{1},\overline{3},\overline{7},\overline{9}}$。
若从某个非空数集中任选两个元素( 同一元素可重复选出 ),选出的这两个元素通过某种( 或几种 )运算后的得数仍是该数集中的元素,那么,就说该集合对于这种( 或几种 )运算是封闭的。$\\$例如若一个集合中的元素,如果能够做到做加法运算的结果还在这个集合中,就说这个集合对加法运算封闭。$\\$ 例如 $\N$ 对加法、乘法运算是封闭的;$\Z$ 对加、减、乘法运算是封闭的;$\mathbb{Q}, \mathbb{C}$ 对四则运算是封闭的。
简化剩余系关于模 $m$ 乘法封闭。这是因为若 $a,b\ (1\leq a,b\leq m)$ 与 $m$ 互质,则 $ab$ 也与 $m$ 互质。$\\$由余数的定义得 $ab\ \mathrm{mod}\ m$ 也与 $m$ 互质,即 $ab\ \mathrm{mod}\ m$ 也属于 $m$ 的简化剩余系。
- 费马小定理:若 $p$ 是质数,则对于任意整数 $a$,有 $a^p\equiv a\ (\mathrm{mod}\ p)$.
- 欧拉定理:若正整数 $a,n$ 互质,则 $a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)$.
证明:设 $n$ 的简化剩余系为 $\set{\overline{a_1},\overline{a_2},\dots,\overline{a_{\varphi(n)}}}$. $\forall a_i,a_j$,若 $a\cdot a_i\equiv a\cdot a_j\ (\mathrm{mod}\ n)$,则 $a\cdot(a_i-a_j)\equiv 0.$ 因为 $a,n$ 互质,所以 $a_i\equiv a_j$. 故当 $a_i\neq a_j$ 时,$aa_i,aa_j$ 也代表不同的同余类。
又因为简化剩余系关于模 $m$ 乘法封闭,故 $\overline{aa_1}$ 也在简化剩余系集合中。因此,集合 $\set{\overline{a_1},\overline{a_2},\dots,\overline{a_{\varphi(n)}}}$ 与集合 $\set{\overline{aa_1},\overline{aa_2},\dots,\overline{aa_{\varphi(n)}}}$ 都能表示 $n$ 的简化剩余系。综上所述:
$$a^{\varphi(n)}a_1a_2\dots a_{\varphi(n)}\equiv(aa_1)(aa_2)\dots(aa_{\varphi(n)})\equiv a_1a_2\dots a_{\varphi(n)}\ (\mathrm{mod}\ n)$$
因此 $a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)$。当 $p$ 为质数时,满足 $\varphi(p)=p-1$,两边同乘 $a$ 即可得到费马小定理。
另外,当 $a$ 是 $p$ 的倍数,费马小定理显然成立。
---
- 欧拉定理的推论:若正整数 $a,n$ 互质,则对于任意正整数 $b$,有 $a^b\equiv a^{b\ \mathrm{mod}\ \varphi(n)}\ (\mathrm{mod}\ n)$
证明:设 $b=q\cdot \varphi(n)+r$,其中 $0\leq r<\varphi(n)$,即 $r=b\ \mathrm{mod}\ \varphi(n)$. 于是有:
$$a^b\equiv a^{q\cdot\varphi(n)+r}\equiv (a^{\varphi(n)})^q\cdot a^r\equiv 1^q\cdot a^r\equiv a^r\equiv a^{b\ \mathrm{mod}\ \varphi(n)}\ (\mathrm{mod}\ n)$$
证毕。面对 $a+b,a-b,a\cdot b$ 这样的算式,可以在计算前先把 $a,b$ 对 $p$ 取模。面对 $a^b$ 这样的乘方算式,可以先把底数对 $p$ 取模、指数对 $\varphi(p)$ 取模,再计算乘方。
即 $a^b\equiv (a\ \mathrm{mod}\ p)^{b\ \mathrm{mod}\ \varphi(p)}\ (\mathrm{mod}\ p)$
---
- 扩展欧拉定理
$$a^b\equiv\begin{cases}a^{b\ \mathrm{mod}\ \varphi(m)}&\text{if }\gcd(a,m)=1\\ a^b&\text{if }\gcd(a,m)\neq 1,b<\varphi(m)\\ a^{b\ \mathrm{mod}\ \varphi(m)+\varphi(m)}&\text{if }\gcd(a,m)\neq 1,b\geq\varphi(m)\end{cases}\ (\mathrm{mod}\ m)$$
证明十分显然,略。
---
- 若正整数 $a,n$ 互质,则满足 $a^x\equiv 1\ (\mathrm{mod}\ n)$ 的最小正整数 $x_0$ 是 $\varphi(n)$ 的约数。
反证法,假设满足 $a^x\equiv 1\ (\mathrm{mod}\ n)$ 的最小正整数 $x_0$ 不能整除 $\varphi(n)$.
设 $\varphi(n)=qx_0+r\ (0<r<x_0)$,因为 $a^{x_0}\equiv 1\ (\mathrm{mod}\ n)$,所以 $a^{qx_0}\equiv 1\ (\mathrm{mod}\ n)$. 根据欧拉定理 $a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)$,所以 $a^r\equiv 1\ (\mathrm{mod}\ n)$. 这与 $x_0$ 最小矛盾。故假设不成立,原命题成立。
### 中国剩余定理
设 $m_1,m_2,\dots,m_n$ 是两两互质的整数,$m=\displaystyle\prod_{i=1}^n m_i,M_i=\frac{m}{m_i},t_i$ 是线性同余方程 $M_it_i\equiv 1\ (\mathrm{mod}\ m_i)$ 的一个解。对于任意的 $n$ 个整数,方程组
$$\begin{cases}x\equiv a_1\ (\mathrm{mod}\ m_1) \\ x\equiv a_2\ (\mathrm{mod}\ m_2)\\ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ x\equiv a_n\ (\mathrm{mod}\ m_n)\end{cases}$$
有整数解,解为 $x=\displaystyle\sum_{i=1}^{n}a_iM_it_i$,通解可以表示为 $x+km(k\in\Z)$,最小非负整数解为 $x\ \mathrm{mod}\ m$.
证明:因为 $\displaystyle M_i=\frac{m}{m_i}$ 是除了 $m_i$ 之外所有模数的倍数,所以 $\forall k\neq i,a_iM_it_i\equiv 0\ (\mathrm{mod}\ m_i)$,$\\ \ \ \ \ \ \ \ \ \ \ \text{}$所以代入 $x=\displaystyle\sum_{i=1}^{n}a_iM_it_i$,原方程组成立。
### 威尔逊定理
- $p$ 为素数 $\xLeftrightarrow{}(p-1)!\equiv -1\ (\mathrm{mod}\ p)$
证明:
1. 充分性
对于 $p$ 不是素数的情况,有 $\begin{cases}
p=1 & (1-1)!\equiv 0\ (\mathrm{mod}\ 1) \\
p=4 & (4-1)!\equiv 2\ (\mathrm{mod}\ 4) \\
p>4 & 分类讨论得出\ (p-1)!\equiv 0\ (\mathrm{mod}\ p)
\end{cases}$
(a) 当 $p$ 为完全平方数。
则 $p=k^2$ 且 $k>2$,用相减法比较 $2k$ 与 $p$ 的大小得 $2k<p$,于是有
$$\begin{aligned}(p-1)!&=1\times 2\times\dots\times k\times\dots\times 2k\times\dots\times (p-1)\\ &=2nk^2\\&=2np\end{aligned}$$
所以 $(p-1)!\equiv 0\ (\mathrm{mod}\ p)$ 且 $p$ 为完全平方数。
(b) 当 $p$ 不为完全平方数。
则 $p$ 可以表示为两个不相等的数 $a$ 和 $b$ 的乘积,设 $a<b$,则有 $p=ab,1<a<b<p$
$$\begin{aligned}(p-1)!&=1\times 2\times\dots\times a\times\dots\times b\times\dots\times (p-1)\\&=a\times b\times n\\ &=np\end{aligned}$$
所以 $(p-1)!\equiv 0\ (\mathrm{mod}\ p)$ 且 $p$ 不为完全平方数。
2. 必要性
当 $p$ 为素数时,考虑二次剩余式 $x^2\equiv 1\ (\mathrm{mod}\ p)$,化简得 $(x-1)(x+1)\equiv 0\ (\mathrm{mod}\ p)$
于是 $x\equiv 1\ (\mathrm{mod}\ p)$ 或 $x\equiv p-1\ (\mathrm{mod}\ p)$。现在先抛开 $1$ 和 $p-1$ 不管,
$\forall a\in [2,p-2]$,必然存在一个和它不相等的逆元 $a^{-1}\in[2,p-2]$,满足 $aa^{-1}\equiv 1\ (\mathrm{mod}\ p)$
所以必然有 $\displaystyle\frac{p-3}{2}$ 对数相乘的乘积为 $1$,即 $(p-2)!\equiv 1\ (\mathrm{mod}\ p)$
等式两边同时乘 $p-1$ 就得到威尔逊定理。
例题:$n\in\N^*$ 且 $n\leq 10^6$,求 $S_n$.
$$S_n=\displaystyle\sum_{k=1}^{n}\left\lfloor\frac{(3k+6)!+1}{3k+7}-\left\lfloor\frac{(3k+6)!}{3k+7}\right\rfloor\right\rfloor$$
令 $d=3k+7$,原式化简为
$$S_n=\displaystyle\sum_{k=1}^{n}\left\lfloor\frac{(d-1)!+1}{d}-\left\lfloor\frac{(d-1)!}{d}\right\rfloor\right\rfloor$$
由威尔逊定理,当 $d$ 为素数时,$\displaystyle\frac{(d-1)!+1}{d}$ 必然是整数,而 $\displaystyle\left\lfloor\frac{(d-1)!}{d}\right\rfloor$ 必然比 $\displaystyle\frac{(d-1)!+1}{d}$ 小 $1$,于是有:
$$\begin{cases}p\ 为素数 & \displaystyle\left\lfloor\frac{(d-1)!+1}{d}-\left\lfloor\frac{(d-1)!}{d}\right\rfloor\right\rfloor=1 \\ p\ 为合数 & \displaystyle\left\lfloor\frac{(d-1)!+1}{d}-\left\lfloor\frac{(d-1)!}{d}\right\rfloor\right\rfloor=0\end{cases}$$
所以只需统计 $[1,3\times 10^6+7]$ 中的素数即可得出答案。
## 拉格朗日定理
若 $p$ 是质数,则对于模 $p$ 意义下的 $n$ 次整系数多项式 $f(x)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_0(p\nmid a_n)$ 同余方程 $f(x)\equiv 0(\mathrm{mod}\ p)$ 至多有 $n$ 个不同的解。
## 牛顿迭代
对于在 $[a,b]$ 上连续且单调的函数 $f(x)$,牛顿迭代法可用于求解方程 $f(x)=0$ 的近似解。
初始时先从给定的 $f(x)$ 和近似解 $x_0$ 开始,$x_0$ 可以是随机数。然后我们可以得到 $f(x_0)$.
接着,画出与 $f(x)$ 切于点 $(x_0,f(x_0))$ 的直线 $l_0$,将 $l_0$ 与 $x$ 轴的交点横坐标记为 $x_1$,$x_1$ 就是更优的近似解。
重复这个迭代过程,可以得到:
$$f'(x_i)=\frac{f(x_i)}{x_i-x_{i+1}} \implies x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}$$
优点:收敛率是平方级别的,这意味着每次迭代后近似解的精确数位会翻倍。
缺点:不能处理重复的根;解可能在拐点附近发散;解可能在局部极小值或最大值附近振荡;当斜率接近于零时,解可能发散或到达不同的根。
## 拉格朗日插值法
由 $n$ 个点可以唯一确定一个多项式 $y=f(x)$, 当已知这 $n$ 个点的坐标要求 $f(k)$ 有:
$$f(k)=\displaystyle\sum_{i=1}^{n}\left(y_i\displaystyle\prod_{i\neq j}^{1\leq j\leq n}\frac{k-x_j}{x_i-x_j}\right)$$
如果已知 $f(1),f(2),\dots,f(n),f(n+1)$,要求 $f(x)$ 有:
$$f(x)=\displaystyle\sum_{i=1}^{n+1}(-1)^{n+1-i}\cdot y_i\cdot\frac{\displaystyle\prod_{j=1}^{n+1}(x-j)}{(i-1)!(n+1-i)!(x-i)}$$
# 组合计数
- 加法原理( 分类 ),乘法原理( 分步 )。
- 排列:从 $n$ 个不同元素中取 $m$ 个排成一列,**考虑顺序**,产生不同排列的数量为 $\\ A_n^m$ ( 也可记作 $P_n^m$ ) $=\displaystyle \frac{n!}{(n-m)!}=n\times(n-1)\times(n-2)\times\dots\times(n-m+1)$
- 组合:从 $n$ 个不同元素中取 $m$ 个排成一列,**不考虑顺序**,产生不同组合的数量为 $\\ \displaystyle\begin{pmatrix}n \\ m\end{pmatrix}=C_n^m=\frac{n!}{m!(n-m)!}=\frac{n\times(n-1)\times\dots\times(n-m+1)}{m\times(m-1)\times\dots\times 2\times 1}$
性质:
1. $C_n^m=C_n^{n-m}$
2. $C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$
3. $\displaystyle\frac{k}{n}C_n^k=C_{n-1}^{k-1}$
4. $\displaystyle\frac{n}{n-m}C_{n-1}^m=C_n^m$
5. $\displaystyle\sum_{i=0}^{n}C_n^i=C_n^0+C_n^1+C_n^2+\dots+C_n^n=2^n$
6. $C_n^0+C_n^2+C_n^4+\dots=C_n^1+C_n^3+C_n^5+\dots$
- 组合数的应用
1. 有 $n$ 个**完全相同**的元素,要求将其分为 $k$ 组,保证每组至少有一个元素,一共有多少种分法?
考虑拿 $k-1$ 块板子插入到 $n$ 个元素两两形成的 $n-1$ 个空里面,答案为 $\red{C_{n-1}^{k-1}}$,本质是求 $x_1+x_2+\dots+x_k=n$ 的正整数解的组数。
2. 若问题变换一下,每组允许为空?
考虑创造条件转化成有限制的问题一,先借 $k$ 个元素过来,在这 $n+k$ 个元素形成的 $n+k-1$ 个空里面插板,答案为 $\red{C_{n+k-1}^n}$,本质是求 $x_1+x_2+\dots+x_k=n$ 的非负整数解的组数。
3. 再扩展一步,要求对于第 $i$ 组,至少要分到 $a_i$ 个元素呢?( $\sum a_i\leq n$ )
本质是求 $x_1+x_2+\dots+x_k=n$ 的整数解的数目。
类比无限制的情况,我们借 $\sum a_i$ 个元素过来,保证第 $i$ 组能至少分到 $a_i$ 个,也就是令 $x_i'=x_i-a_i$ 且 $x_i'\geq 0$
得到新方程
$$(x_1'+a_1)+(x_2'+a_2)+\dots+(x_k'+a_k)=n\implies\sum_{i=1}^{k}x_i'=n-\sum a_i$$
答案为 $\red{C_{n-\sum a_i+k-1}^{k-1}}$
4. 从 $n$ 个连续整数选 $k$ 个,这 $k$ 个数中两两都不相邻的组合有 $\red{C_{n-k+1}^k}$ 种。
5. 若将 $N$ 个**不同的**的元素分成 $a$ 组,第 $i$ 组的数量为 $n_i$,其中相同的组共有 $b$ 类,第 $k$ 类的相同组的个数为 $s_k$,则共有 $\displaystyle\red{\boxed{\frac{N!}{\displaystyle\prod_{i=1}^a(n_i!)\times\prod_{k=1}^b(s_k!)}}}$ 种方法。
原理:$\displaystyle C_{N}^{n_1}C_{N-n_1}^{n_2}\dots C_{n_a}^{n_a}=\frac{N!}{n_1!\times n_2!\times\dots\times n_a!}=\frac{N}{\displaystyle\prod_{i=1}^a(n_i!)}$ 用于消除组内排序。$\displaystyle\prod_{k=1}^b(s_k!)$ 用于消除组间排序。
例 $1$:将 $6$ 本不同的书分给甲乙丙 $3$ 人,每人 $2$ 本,有多少种分法?
这是不同的 $3$ 组,即没有相同的组,故不用消除组间排序。答案是 $\displaystyle\frac{6!}{2!2!2!}=90$.
如果是分成三组每组 $2$ 本,那就要消除组间排序。答案是 $\displaystyle\frac{6!}{(2!2!2!)\times 3!}=15$.
例 $2$:将 $14$ 个人分成人数分别为 $2,2,2,4,4$ 的无区别的五组,有多少种分法?
$$\frac{14!}{(2!2!2!4!4!)(3!2!)}=1576575$$
### 定理
- 二项式定理:
$$(a+b)^n=\displaystyle\sum_{k=0}^{n}C_n^ka^kb^{n-k}\ \ \ \ \ \ \ (ax+by)^n=\displaystyle\sum_{k=0}^{n}C_n^ka^kb^{n-k}x^ky^{n-k}$$
例如:$(2x+3y)^3=8x^3+36x^2y+54xy^2+27y^3\\ \ \ \ \ \ \ \ \ \ \ \displaystyle\left(3x+\frac{5}{x^2}\right)^4=81x^4+540x+\frac{1350}{x^2}+\frac{1500}{x^5}+\frac{625}{x^8}$
- 三项式定理:
$$(a+b+c)^n=\sum_{i+j+k=n}\frac{n!}{i!j!k!}a^ib^jc^k$$
例如:$\displaystyle \begin{aligned}(a+b+c)^3&=\frac{3!}{3!0!0!}a^3+\frac{3!}{0!3!0!}b^3+\frac{3!}{0!0!3!}c^3+\frac{3!}{2!1!0!}a^2b+\frac{3!}{2!0!1!}a^2c\\&+\frac{3!}{1!2!0!}ab^2+\frac{3!}{0!2!1!}b^2c+\frac{3!}{1!0!2!}ac^2+\frac{3!}{0!1!2!}bc^2+\frac{3!}{1!1!1!}abc\\&=a^3+b^3+c^3+3a^2b+3a^2c+3b^2a+3b^2c+3c^2a+3c^2b+6abc\end{aligned}$
例 1:求 $(x+2y-3z)^6$ 中 $xy^2z^3$ 项。答案为 $\displaystyle\frac{6!}{1!2!3!}x(2y)^2(-3z)^3=-6480xy^2z^3$
例 2:求 $\displaystyle \left(x+\frac{2}{x}-1\right)^4$ 的常数项。
$$\frac{4!}{0!0!4!}(-1)^4+\frac{4!}{1!1!2!}x\cdot\frac{2}{x}\cdot(-1)^2+\frac{4!}{2!2!0!}x^2\cdot\left(\frac{2}{x}\right)^2=1+24+24=49$$
若扩展成多项式的形式,有:
$$(x_1+x_2+\dots+x_t)^n=\displaystyle\sum_{满足\ n_1+n_2+\dots+n_t=n\ 的非负整数解}\begin{pmatrix}n \\ n_1,n_2,\dots,n_t\end{pmatrix}x_1^{n_1}x_2^{n_2}\dots x_t^{n_t}$$
其中 $\begin{pmatrix}n \\ n_1,n_2,\dots,n_t\end{pmatrix}$ 是多项式系数,满足 $\displaystyle\sum \begin{pmatrix}n \\ n_1,n_2,\dots,n_t\end{pmatrix}=t^n$.
或者用三项式展开的形式也行。
- 范德蒙德卷积( 范德蒙德恒等式 )
$$\displaystyle\sum_{i=0}^k C_n^iC_m^{k-i}=C_n^0C_m^k+C_n^1C_m^{k-1}+\dots+C_n^kC_m^0=C_{n+m}^k$$
证明:比对 $(1+x)^n(1+x)^m=(1+x)^{n+m}$ 两边 $x^k$ 系数即可。
如果我们令 $n=m=k$,可以得到 $\displaystyle C_{2n}^n=\sum_{i=0}^k (C_n^i)^2$
- $\text{Lucas}$ 卢卡斯定理:( $p$ 是质数,$1\leq m\leq n$ )
$$C_n^m\equiv C_{n\ \text{mod}\ p}^{m\ \text{mod}\ p}\times C_{n/p}^{m/p}\ (\text{mod}\ p)$$
### 容斥原理
设 $S_1,S_2,\dots,S_n$ 为有限集合,$|S|$ 表示集合 $S$ 的大小,则:
$$|\displaystyle\bigcup_{i=1}^{n}S_i|=\displaystyle\sum_{i=1}^{n}|S_i|-\displaystyle\sum_{1\leq i<j\leq n}|S_i\bigcap S_j|+\displaystyle\sum_{1\leq i<j<k\leq n}|S_i\bigcap S_j\bigcap S_k|+\dots+(-1)^{n+1}|S_1\bigcap\dots\bigcap S_n|$$
1. 将 $2$ 个蓝球,$4$ 个黄球,$4$ 个绿球按任意次序从左到右排列,使得 $2$ 个蓝球不相邻且存在 $2$ 个相邻的绿球,则不同的排列有几种 ?( 认为相同颜色的球都一样 )
$A=\set{蓝球相邻},B=\set{任意两个绿球不相邻},S$ 为全集,则
$$|S|=\frac{10!}{4!4!2!}=3150\ \ \ \ |A|=\frac{9!}{4!4!1!}=630\ \ \ \ |B|=C_7^4C_6^2=525\ \ \ \ |A\cap B|=C_6^4C_5^1$$
$$ans=4(|S|-|A\cup B|)=4(|S|-|A|-|B|+|A\cap B|)=8280$$
2. $7$ 把钥匙 $7$ 把锁,随机开锁,则 $D_1,D_2,D_3$ 三把钥匙不能打开对应锁的概率是 ?
设 $D_i$ 打开对应锁的事件为 $X_i$,则 $$|X_i|=6!,|X_i\cap X_j|=5!,|X_i\cap X_j\cap X_k|=4!\ \ \ \ (i<j<k)$$
因此所求为 $\displaystyle\frac{7!-3\times 6!+3\times 5!-4!}{7!}=\frac{67}{105}$.
3. $6$ 对夫妻围着有 $12$ 个座位的圆桌入座,每人坐在不同座位上,$6$ 位女士已经优先入座且每相邻两位女士间恰有一个空座位,将她们顺时针记为 $A\sim F$。已知 $A,B,C,D$ 这 $4$ 位女士各自的丈夫都不坐在与自己妻子相邻的空座位上,则入座方式有多少种 ?
设 $U$ 为全集( 任意坐 ),其中 $A$ 的丈夫坐在 $A$ 身边的、$6$ 位男士的坐法组成的集合为 $X_1$,类似定义 $X_2,X_3,X_4$,问题相当于求
$$\begin{aligned}|\overline{X_1}\cap\overline{X_2}\cap\overline{X_3}\cap\overline{X_4}|&=|U|-\sum_{i=1}^4 |X_i|+\sum_{1\leq i<j\leq 4}|X_i\cap X_j|\\&-\sum_{1\leq i<j<k\leq 4}|X_i\cap X_j\cap X_k|+|X_1\cap X_2\cap X_3\cap X_4|\\&=6!-C_8^1\times 5!+C_7^2\times 4!-C_6^3\times 3!+C_5^4\times 2!=154\end{aligned}$$
- 第 1 类 $\mathrm{Stirling}$ 数:$1$ ~ $n$ 的排列有 $m$ 个环:
$$S_1(n,m)=S_1(n-1,m-1)+S_1(n-1,m)\times(n-1)$$
- 第 2 类 $\mathrm{Stirling}$ 数:$n$ 个不同的球放入 $m$ 个相同盒子且盒子非空:
$$S_2(n,m)=S_2(n-1,m-1)+S_2(n-1,m)\times m=\sum_{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}$$
表示将新球单独放在一个盒子或者放入一个现有盒子。后面递推式的证明需要二项式反演。
- $\mathrm{Eulerian\ Number}$ 欧拉数( 注意与 $\gamma$ 和 $e$ 等与欧拉相关的数学常数无关 ):从 $1$ 到 $n$ 中正好满足 $m$ 个元素大于前一个元素条件的排列个数。
$$A(n,m)=\begin{cases}0&m>n\ \mathrm{or}\ n=0\\1&m=0\\(n-m)\cdot A(n-1,m-1)+(m+1)\cdot A(n-1,m)& \mathrm{otherwise}\end{cases}=\sum_{k=0}^m(-1)^{m-k}C_{n+1}^k(m-k)^n$$
- $\text{Catalan}$ 卡特兰数列:给定 $n$ 个 $0$ 和 $n$ 个 $1$,它们按照某种顺序排成长度为 $2n$ 的序列,满足任意前缀中 $0$ 的个数都不少于 $1$ 的个数的序列的数量为:
$$C_n=\frac{C_{2n}^n}{n+1}=\sum_{k=1}^n C_{k-1}\cdot C_{n-k}=\frac{4n-2}{n+1}C_{n-1}=C_{2n}^n-C_{2n}^{n-1}$$
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| :----------------: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :----: | :----: | :-----: |
| $C_n$ | $1$ | $2$ | $5$ | $14$ | $42$ | $132$ | $429$ | $1430$ | $4862$ | $16796$ |
以下问题都与 $\text{Catalan}$ 数有关:
1. $n$ 个左括号和 $n$ 个右括号组成的合法括号序列的数量为 $C_n$
2. $1,2,\dots,n$ 经过一个栈,形成的合法出栈序列的数量为 $C_n$
3. $n$ 个节点构成的不同二叉树的数量为 $C_n$,$n$ 个节点的 $m$ 叉树有 $\displaystyle\frac{1}{n}C_{nm}^{n-1}$
4. 在平面直角坐标系上,每一步只能向上或向右走,从 $(0,0)$ 走到 $(n,n)$ 并且两个端点外不接触直线 $y=x$ 的路线数量为 $2C_{n-1}$
5. 对于一个凸多边形的顶点数为 $n$,$C_{n-2}$ 代表所有可能的三角剖分的数量。( 对角线不相交下分成若干个三角形 )
6. 在圆上选择 $2n$ 个点,将这些点成对连接起来使得所得到的 $n$ 条线段不相交的方法数为 $C_n$
7. 由 $n$ 个 $+1$ 和 $n$ 个 $-1$ 组成的 $2n$ 个数 $a_1,a_2,\dots,a_{2n}$,其部分和满足 $\displaystyle\sum_{i=1}^k a_i\geq 0$,有 $C_n$ 个满足条件的数列。
- 错位排列:$1$ ~ $n$ 的排列,第 $i$ 个位置上均不为 $i$:
用容斥原理推导:正整数 $1,2,\dots,n$ 的全排列有 $n!$ 种,其中第 $k$ 位是 $k$ 的排列有 $(n-1)!$ 种,由于所求的是错排的种数,所以应当减去这些排列;但是此时把同时有两个点放对位置的排列多排除了一次,应补上;在补上时,把同时有三个数不错排的排列多补上了一次,应排除;……;继续这一过程,得到错排的排列种数为
$$D(n)=n!-\frac{n!}{1!}+\frac{n!}{2!}-\frac{n!}{3!}+\dots=\red{n!\sum_{k=2}^n\frac{(-1)^k}{k!}=\left\lfloor\frac{n!}{e}+\frac{1}{2}\right\rfloor}$$
后面是简化公式,参考百度。随着元素数量的增加,形成错位排列的概率 $P=\displaystyle\lim_{n\to\infty}\frac{D(n)}{n!}=\frac{1}{e}$
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| $D(n)$ | $0$ | $1$ | $2$ | $9$ | $44$ | $265$ | $1854$ | $14833$ | $133496$ | $1334961$ |
<!-- 第一步,把第 $n$ 个元素放在一个位置,比如位置 $k$,一共有 $n-1$ 种方法;
第二步,放编号为 $k$ 的元素,这时有两种情况:①把它放到位置 $n$,那么,对于剩下的 $n-1$ 个元素,由于第 $k$ 个元素放到了位置 $n$,剩下 $n-2$ 个元素就有 $D(n-2)$ 种方法;②第 $k$ 个元素不把它放到位置 $n$,这时,对于这 $n-1$ 个元素,有 $D(n-1)$ 种方法。
$$D(n)=(n-1)[D(n-1)+D(n-2)]$$
特别的,$D(1)=0,D(2)=1$,接下来推导 $D(n)$ 的通项,设 $D(k)=k!N(k),N(1)=0,N(2)=\frac{1}{2}$。
$$n!N(n)=(n-1)(n-1)!N(n-1)+(n-1)!N(n-2)\implies nN(n)=(n-1)N(n-1)+N(n-2)$$
$$N(n)-N(n-1)=\frac{-1}{n}[N(n-1)-N(n-2)]=\dots=\frac{(-1)^{n-2}}{\frac{n!}{2!}}[N(2)-N(1)]=\frac{(-1)^n}{n!}$$
$$N(n)=\sum_{k=2}^n\frac{(-1)^k}{k!}\implies D(n)=n!\sum_{k=2}^n\frac{(-1)^k}{k!}$$ -->
- 圆排列( 循环排列 ):$m$ 个数中选 $n$ 个不同的排列成一个环形。
计算公式推导:先推 $n=m$ 时的公式。一个环打开成直线,有 $n!$ 种。合起来转一圈,有 $n$ 个是相同的,于是 $n$ 个元素的循环全排列种数为 $(n-1)!$。于是通项便为 $\displaystyle C_m^n(n-1)!=\red{\frac{1}{n}A_m^n}$
- 其他:从 $(0,0)$ 走到 $(m,n)$ 的非降路径数为 $C_{n+m}^m$
# 常用三角函数值
| $\alpha$ | $\sin\alpha$ | $\cos\alpha$ | $\tan\alpha$ | $\cot\alpha$ |
| :-------------: | :---------------------------: | :---------------------------: | :------------------: | :------------------: |
| $0\degree $ | $0$ | $1$ | $0$ | $/$ |
| $15\degree $ | $\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}$ | $\displaystyle\frac{\sqrt{6}+\sqrt{2}}{4}$ | $2-\sqrt{3}$ | $2+\sqrt{3}$ |
| $18\degree $ | $\displaystyle\frac{\sqrt{5}-1}{4}$ | $\displaystyle\frac{\sqrt{10+2\sqrt{5}}}{4}$ | $\displaystyle\frac{\sqrt{6-2\sqrt{5}}}{2}$ | $\displaystyle\frac{2}{\sqrt{6-2\sqrt{5}}}$ |
| $22.5\degree $ | $\displaystyle\frac{\sqrt{2-\sqrt{2}}}{2}$ | $\displaystyle\frac{\sqrt{2+\sqrt{2}}}{2}$ | $\sqrt{2}-1$ | $\sqrt{2}+1$ |
| $30\degree $ | $\displaystyle\frac{1}{2}$ | $\displaystyle\frac{\sqrt{3}}{2}$ | $\displaystyle\frac{\sqrt{3}}{3}$ | $\sqrt{3}$ |
| $36\degree $ | $\displaystyle\sqrt{\frac{5-\sqrt{5}}{8}}$ | $\displaystyle\frac{\sqrt{5}+1}{4}$ | $\displaystyle\sqrt{5-2\sqrt{5}}$ | $\displaystyle\frac{1}{\sqrt{5-2\sqrt{5}}}$ |
| $36.87\degree $ | $\displaystyle\frac{3}{5}$ | $\displaystyle\frac{4}{5}$ | $\displaystyle\frac{3}{4}$ | $\displaystyle\frac{4}{3}$ |
| $45\degree $ | $\displaystyle\frac{\sqrt{2}}{2}$ | $\displaystyle\frac{\sqrt{2}}{2}$ | $1$ | $1$ |
| $53.13\degree $ | $\displaystyle\frac{4}{5}$ | $\displaystyle\frac{3}{5}$ | $\displaystyle\frac{4}{3}$ | $\displaystyle\frac{3}{4}$ |
| $60\degree $ | $\displaystyle\frac{\sqrt{3}}{2}$ | $\displaystyle\frac{1}{2}$ | $\sqrt{3}$ | $\displaystyle\frac{\sqrt{3}}{3}$ |
| $63.43\degree $ | $\displaystyle\frac{2\sqrt{5}}{5}$ | $\displaystyle\frac{\sqrt{5}}{5}$ | $2$ | $\displaystyle\frac{1}{2}$ |
| $71.57\degree $ | $\displaystyle\frac{3\sqrt{10}}{10}$ | $\displaystyle\frac{\sqrt{10}}{10}$ | $3$ | $\displaystyle\frac{1}{3}$ |
| $75\degree $ | $\displaystyle\frac{\sqrt{6}+\sqrt{2}}{4}$ | $\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}$ | $2+\sqrt{3}$ | $2-\sqrt{3}$ |
| $75.96\degree $ | $\displaystyle\frac{4\sqrt{17}}{17}$ | $\displaystyle\frac{\sqrt{17}}{17}$ | $4$ | $\displaystyle\frac{1}{4}$ |
| $90\degree $ | $1$ | $0$ | $/$ | $0$ |
# 常用数表
| $x$ | $\ln{x}$ | $\lg{x}$ | $\sqrt{x}$ | $2^x$ | $3^x$ | $x^2$ | $x^3$ | $x!$ |
| :-----------: | :-------: | :-------: | :--------: | :------: | :------: | :------: | :------: | :-------: |
| $\displaystyle\frac{1}{3}$ | $-1.0986$ | $-0.4771$ | $0.5773$ | $1.2599$ | $1.4422$ | $0.1111$ | $0.0370$ | $/$ |
| $\displaystyle\frac{1}{2}$ | $-0.6931$ | $-0.3010$ | $0.7071$ | $1.4142$ | $1.7321$ | $0.25$ | $0.125$ | $/$ |
| $1$ | $0$ | $0$ | $1$ | $2$ | $3$ | $1$ | $1$ | $1$ |
| $2$ | $0.6931$ | $0.3010$ | $1.4142$ | $4$ | $9$ | $4$ | $8$ | $2$ |
| $3$ | $1.0986$ | $0.4771$ | $1.7321$ | $8$ | $27$ | $9$ | $27$ | $6$ |
| $4$ | $1.3862$ | $0.6021$ | $2$ | $16$ | $81$ | $16$ | $64$ | $24$ |
| $5$ | $1.6094$ | $0.6989$ | $2.2361$ | $32$ | $243$ | $25$ | $125$ | $120$ |
| $6$ | $1.7917$ | $0.7781$ | $2.4495$ | $64$ | $729$ | $36$ | $216$ | $720$ |
| $7$ | $1.9459$ | $0.8451$ | $2.6458$ | $128$ | $2187$ | $49$ | $343$ | $5040$ |
| $8$ | $2.0794$ | $0.9031$ | $2.8284$ | $256$ | $6561$ | $64$ | $512$ | $40320$ |
| $9$ | $2.1972$ | $0.9542$ | $3$ | $512$ | $19683$ | $81$ | $729$ | $362880$ |
| $10$ | $2.3025$ | $1$ | $3.1623$ | $1024$ | $59049$ | $100$ | $1000$ | $3628800$ |
### 常用常数值
- $\pi=\arccos(-1)=\sqrt{6\displaystyle\sum^{\infty}_{i=1}\frac{1}{i^2}}\approx 3.1415926535 \ 8979323846 \ 2643383279 \ 5028841971 \ 6939937510$
- $e=\displaystyle\lim_{x\to +\infty}\left(1+\frac{1}{x}\right)^x=\displaystyle\sum^{\infty}_{i=0}\frac{1}{i!}\approx 2.7182818284 \ 5904523536 \ 0287471352 \ 6624977572 \ 4709369995 $
- 黄金数 $\displaystyle\varphi=\frac{\sqrt{5}-1}{2}\approx 0.6180339887 \ 4989484820 \ 4586834365 \ 63811$
- 真空光速 $c\approx 299792458 \ \text{m}/\text{s}$
- 重力加速度 $g\approx 9.8\ \text{m}/\text{s}^2$ ( 纬度越高 $g$ 值越大 )
- 阿伏伽德罗常数 $N_A \approx 6.02214076 \times 10^{23}\text{mol}^{-1}$
- 引力常量 $G\approx 6.67\times 10^{-11}\text{m}^3 \text{kg}^{-1} \text{s}^{-2}$
- 标准状况 STP($0\degree \text{C},101.325\text{kPa}$)下 $1\text{mol}$ 气体所占的体积约为 $22.414\text{L}$
- $25\degree \text{C},101.325\text{kPa}$下 $1\text{mol}$ 气体所占的体积约为 $24.466\text{L}$
- 静电力常量 $k\approx 8.987551\times 10^9 \text{N}\cdot\text{m}^2 \text{/C}^2$
- 元电荷 $e=1.60217646283\times 10^{-19}\text{C}$
- 电子质量 $m_e=9.11\times 10^{-31}\text{kg}$
- 电子比荷 $\displaystyle\frac{e}{m_e}=1.76\times 10^{-11}\text{C / kg}$
- $100$ 以内的质数( 一三行表序号,二四行才是质数 )
| $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ | $13$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $2$ | $3$ | $5$ | $7$ | $11$ | $13$ | $17$ | $19$ | $23$ | $29$ | $31$ | $37$ | $41$ |
| $14$ | $15$ | $16$ | $17$ | $18$ | $19$ | $20$ | $21$ | $22$ | $23$ | $24$ | $25$ |
| $43$ | $47$ | $53$ | $59$ | $61$ | $67$ | $71$ | $73$ | $79$ | $83$ | $89$ | $97$ |
# 高等数学
## 中值定理
- 罗尔中值定理:如果函数 $f(x)$ 在 $[a,b]$ 上连续,在 $(a,b)$ 可导,且 $f(a)=f(b)$,那么在 $(a,b)$ 内存在至少一点 $\xi$ 使得 $f'(\xi)=0$.
- 拉格朗日中值定理:如果函数 $f(x)$ 在 $[a,b]$ 上连续,在 $(a,b)$ 可导,那么在 $(a,b)$ 内存在至少一点 $\xi$ 使得 $f(b)-f(a)=f'(\xi)(b-a)$.
- 柯西中值定理:如果函数 $f(x),g(x)$ 在 $[a,b]$ 上连续,在 $(a,b)$ 可导,且 $g'(x)$ 在 $(a,b)$ 内的每一点均不为 $0$,那么在 $(a,b)$ 内存在至少一点 $\xi$ 使得 $\displaystyle\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi)}{g'(\xi)}$.
例如:证明:当 $0<b<a$ 时,$\displaystyle\frac{a-b}{a}<\ln\frac{a}{b}<\frac{a-b}{b}$.
即证 $\displaystyle\frac{1}{a}<\frac{\ln a-\ln b}{a-b}<\frac{1}{b}$. 于是我们构造 $f(x)=\ln x,x\in[b,a]$,因为 $f(x)$ 在 $[a,b]$ 上连续,在 $(b,a)$ 上可导,故由拉格朗日中值定理得 $\exist\xi\in(b,a)$ 使得 $\displaystyle f(a)-f(b)=f'(\xi)(a-b)\implies \ln a-\ln b=\frac{1}{\xi}(a-b)\implies \frac{\ln a-\ln b}{a-b}=\frac{1}{\xi}$
因 $0<b<\xi<a$,故 $\displaystyle\frac{1}{a}<\frac{1}{\xi}<\frac{1}{b}$,证毕。
## 洛必达法则
- 洛必达法则:当 $x\to a$ 时,$f(x)$ 和 $g(x)$ 同时趋近于 $0$ 或 $\infty$,则:
$$\boxed{\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}}$$
例如:
$$\begin{aligned}\lim_{x \to 2}\frac{x^2-3x+2}{x-2}&=\lim_{x \to 2}\frac{(x-1)(x-2)}{x-2}=\lim_{x \to 2}(x-1)=1\\&\xlongequal{洛必达法则}\lim_{x \to 2}\frac{2x-3}{1}=1\end{aligned}$$
如果不是 $\displaystyle\frac{0}{0}$ 型或 $\displaystyle\frac{\infty}{\infty}$ 型,则需要先变形为 $\frac{0}{0}$ 型或 $\frac{\infty}{\infty}$ 型才能洛。例如:
$$\lim_{x\to 0}x\ln x=\frac{\ln x}{\frac{1}{x} }\xlongequal{洛必达法则}\frac{\frac{1}{x} }{-\frac{1}{x^2} }=-x=0$$
**注意最好不要在解答题中使用洛必达法则。**
例题:$f(x)=x(e^x-1)-ax^2$,当 $x\geq 0$ 时,$f(x)\geq 0$,求实数 $a$ 的取值范围。
题意即证明 $x(e^x-1)\geq ax^2$. 当 $x=0$ 时显然正确。
当 $x>0$ 时,转化为 $\displaystyle a\leq\frac{e^x-1}{x}$,令 $\displaystyle g(x)=\frac{e^x-1}{x}$,则 $\displaystyle g'(x)=\frac{e^x(x-1)+1}{x^2}$,令 $h(x)=e^x(x-1)+1,h'(x)=xe^x>0$,所以 $g(x)$ 在 $(0,+\infty)$ 上 $\uparrow$.
所以 $\displaystyle a\leq\lim_{x\to 0}\frac{e^x-1}{x}\xlongequal{洛必达法则}\lim_{x\to 0}\frac{e^x}{1}=1$,即 $a\leq 1$.
综上所述,$a\in(-\infty,1]$.
## 泰勒展开 Taylor Expansion
[参考](https://zhuanlan.zhihu.com/p/530933700)
我们已经知道以下这几个不等式:
$$e^x\geq x+1\ \ \ \ \ \ \ \ \ln x\leq x-1\ \ \ \ \ \ \ \ e^x\geq ex$$
显然,它们都是对 $x=0$ 或 $x=1$ 处函数的切线拟合,拟合了函数在切点处的导数值。
但是,这么做的精确度往往不足以应对各种难题。那么,我们可不可以多导几次呢 ?让拟合函数在某点处的任意阶导数与原函数的同阶导数相等,精度也许会更高。
而这正是泰勒展开的思想:构造一个多项式( 因为多项式好求导 ),调一调系数,让它在某点处的任意阶导数与原函数的同阶导数相等。
不加解释的给出泰勒展开的式子:
$$p(x)=\frac{f(x_0)}{0!}+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+\dots$$
其中 $p(x)$ 表示一个 $n$ 次多项式的拟合函数,$n\to+\infty$. 注意 $0!=1!=1$.
上式满足:
$$\begin{aligned}
p(x_0)&=f(x_0) \\
p'(x_0)&=f'(x_0) \\
p''(x_0)&=f''(x_0) \\
&\dots \\
p^{(n)}(x_0)&=f^{(n)}(x_0)
\end{aligned}$$
当 $x=x_0$ 时,$p(x)$ 又称 $f(x)$ 的麦克劳林级数,以下统称泰勒级数。而求解函数在某点的泰勒级数就叫泰勒展开。
### 高中常见的泰勒级数
以下令 $x_0=0$.
首先最基础的必背的一定不能忘记的是 $f(x)=e^x$,其任意阶导数 $f^{(n)}(x)=e^x$.
$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots=\sum_{k=0}^{+\infty}\frac{x^k}{k!}$$
然后是三角函数 $\sin$ 和 $\cos$:
$$\sin x=x-\frac{x^3}{6}+\frac{x^5}{120}+\dots=\sum_{k=0}^{+\infty}\frac{(-1)^k}{(2k+1)!}x^{2k+1}$$
$$\cos x=1-\frac{x^2}{2}+\frac{x^4}{24}+\dots=\sum_{k=0}^{+\infty}\frac{(-1)^k}{(2k)!}x^{2k}$$
下面考虑对数函数 $f(x)=\ln(x+1)$ 的泰勒级数,我们先考虑下面的展开:( 证明:生成函数 )
$$\frac{1}{1-x}=1+x+x^2+\dots=\sum_{k=0}^{+\infty}x^k$$
因此我们有
$$f'(x)=\frac{1}{1+x}=1-x+x^2+\dots=\sum_{k=0}^{+\infty}(-1)^kx^k$$
两边同时积分并待定常数,取 $x=0$ 得
$$\ln(x+1)=x-\frac{x^2}{2}+\frac{x^3}{3}+\dots=\sum_{k=0}^{+\infty}\frac{(-1)^{k-1} }{k}x^k$$
对于 $\tan x$,其泰勒展开十分复杂,直接给出:
$$\tan x=x+\frac{x^3}{3}+\frac{2}{15}x^5+\frac{17}{315}x^7+\dots=\sum_{k=1}^{+\infty}\frac{(2^{2k}-1)2^{2k}B_k}{(2k)!}x^{2k-1}$$
这里 $B_k$ 是第 $k$ 个伯努利数的偶数项的绝对值。
### 泰勒展开的应用 - 泰勒放缩
直接去掉后面的高次项即可。
【2022 甲卷】已知 $\displaystyle a=\frac{31}{32},b=\cos\frac{1}{4},c=4\sin\frac{1}{4}$,比较 $a,b,c$ 的大小。
由 $\displaystyle\cos x\geq 1-\frac{x^2}{2}$ 得 $\displaystyle b>1-\frac{\left(\frac{1}{4}\right)^2}{2}=\frac{31}{32}=a$
由 $\displaystyle\sin x\geq x-\frac{x^3}{6}\ \ \ (x\geq 0)$ 得 $\displaystyle c>\frac{95}{96}>a$
构造函数:取 $\displaystyle x=\frac{1}{4}$,则 $\displaystyle b=\cos x,c=\frac{\sin x}{x}$,设 $\displaystyle x=\frac{1}{4}$ 时 $\displaystyle \cos x<\frac{\sin x}{x}$,构造 $f(x)=\sin x-x\cos x\ \ (x>0)$
$\displaystyle f'(x)=x\sin x>0\ \ \left(x\in\left(0,\frac{1}{4}\right]\right)$ 故 $c>b$ 成立,答案为 $c>b>a$.
## $\mathrm{Pade}$ 帕德逼近
好难看不懂捏。直接搬结论了。
| $f(x)=e^x$ | $0$ | $1$ | $2$ |
|:-:|:-:|:-:|:-:|
| $0$ | $1\\$ 先大后小 | $x+1\\$ 恒小于 | $\displaystyle\frac{x^2+2x+2}{2}\\$ 先大后小 |
| $1$ | $\displaystyle\frac{1}{1-x}\\$ 恒大于 | $\displaystyle\frac{2+x}{2-x}\\$ 先小后大 | $\displaystyle\frac{6+4x+x^2}{6-2x}\\$ 恒大于 |
| $2$ | $\displaystyle\frac{2}{x^2-2x+2}\\$ 先小后大 | $\displaystyle\frac{2x+6}{x^2-2x+6}\\$ 恒小于 | $\displaystyle\frac{x^2+6x+12}{x^2-6x+12}\\$ 先大后小 |
| $f(x)=\ln x$ | $0$ | $1$ | $2$ |
|:-:|:-:|:-:|:-:|
| $0$ | $-$ | $x-1\\$ 恒大于 | $\displaystyle\frac{-x^2+4x-3}{2}\\$ 先大后小 |
| $1$ | $-$ | $\displaystyle\frac{2x-2}{x+1}\\$ 先小后大 | $\displaystyle\frac{x^2+4x-5}{4x+2}\\$ 恒大于 |
| $2$ | $-$ | $\displaystyle\frac{12x-12}{5+8x-x^2}\\$ 恒大于 | $\displaystyle\frac{3x^2-3}{6x^2-11x+11}\\$ 先大后小 |
## $\mathrm{Lambert}$ 朗博 W 函数
我们将朗博 W 函数定义为 $f(x)=xe^x$ 的反函数。也就是说,有关方程 $\displaystyle xe^x=a\left(a\geq-\frac{1}{e}\right)$ 可以给出通解 $x=W(a)$( 或 $W_{-1}(a)$,当 $\displaystyle a\in\left(-\frac{1}{e},0\right)$ 时 ),但是 $W(x)$ 没有初等意义的解析式,只有积分式。可以给出泰勒展开式:
$$W(x)=\sum_{n=1}^{\infty}\frac{(-n)^{n-1}}{n!}x^n=x-x^2+\frac{3}{2}x^3-\frac{8}{3}x^4+\frac{125}{24}x^5-\dots$$
如果我们把 $W(x)$ 的定义域限制在 $\displaystyle\left[-\frac{1}{e},+\infty\right)$ 上,取其在 $[-1,+\infty)$ 上的函数值,那么就定义了一个单调递增的函数 $W(x)$;同时将定义域限制在 $\displaystyle\left(-\frac{1}{e},0\right)$ 上,取其在 $(-\infty,-1)$ 上的函数值,那么就定义了一个单调递减的函数 $W_{-1}(x)$.
性质:当 $a\geq 0$ 时,$\boxed{W(x)\cdot e^{W(x)}=x}$,此外可以推出
| $x\ln x=a\implies x=e^{W(a)}$ | $x+\ln x=a\implies x=W(e^a)$ | $\frac{\ln x}{x}=-a\implies x=e^{-W(a)}$ |
|:-:|:-:|:-:|
以及朗博不等式,可以同构证明:$\boxed{xe^x\geq x+\ln x+1}$
例 1:【2023 GD 一模】证明:当 $x>0,xe^{x+1}\geq (a+1)x+\ln x+2$,求 $a$ 范围。答案:$a\leq 0$.
例 2:$\forall x>0,xe^{2x}-kx-\ln x-1\geq 0$,求 $k$ 范围。
分离变量得 $\displaystyle k\leq \frac{xe^{2x}-\ln x-1}{x}=f(x),f'(x)=2e^{2x}+\frac{\ln x}{x^2}=\frac{1}{x}\left(2xe^{2x}+\frac{\ln x}{x}\right)$,令 $f'(x)=0$ 并设 $a=2xe^{2x},\displaystyle \frac{\ln x}{x}=-a$ 解得 $\displaystyle x=\frac{1}{2}W(a)=\frac{W(a)}{a}$,得到 $a=2$,极小值点为 $\displaystyle x=\frac{W(2)}{2}$,代入得
$$f\left(\frac{W(2)}{2}\right)=e^{W(2)}-\frac{\ln\frac{W(2)}{2}}{\frac{W(2)}{2}}-\frac{2}{W(2)}=-\frac{\ln\frac{W(2)}{2}}{\frac{W(2)}{2}}=-\frac{\ln e^{-W(2)}}{\frac{W(2)}{2}}=2$$
因此 $k\in(-\infty,2]$. 其实直接 $xe^{2x}=e^{\ln x+2x}$ 就可以了。
## $\mathrm{Lagrange}$ 拉格朗日乘数法
### 偏导数 - 多元函数的导数
当一个函数有多个自变量时,他们共同影响因变量,我们称之为多元函数。比如 $z=f(x,y)=\sin^2x+\cos^2y$.
根据导数的定义 $\displaystyle\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$ 可以类推出偏导数的定义,即
$$\displaystyle\lim_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\ \ \ \ \ (1) \\ \displaystyle\lim_{\Delta y\to 0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\ \ \ \ \ (2)$$
其中 $(1)$ 式表示函数 $z=f(x,y)$ 在点 $(x,y)$ 处对 $x$ 的偏导数,$(2)$ 式表示函数 $z=f(x,y)$ 在点 $(x,y)$ 处对 $y$ 的偏导数。
我们想求 $f$ 对 $x$ 的偏导数。如果 $f$ 是一个一元函数,这个导数可以记作 $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}$.
类似地,当 $f$ 是多元函数时,这个偏导数就记作 $\displaystyle\frac{\partial f}{\partial x}$.
**求偏导时,把一个变量当作 $x$,其他的变量当作常数,再求导数**。
$\displaystyle E.g.1\ \ \ \ f(x,y)=x+y\ \ \ \ \frac{\partial f}{\partial x}=1+0=1\ \ \ \ \frac{\partial f}{\partial y}=0+1=1$
$\displaystyle E.g.2\ \ \ \ f(x,y)=\sin^2x+\cos^2y\ \ \ \ \frac{\partial f}{\partial x}=(\sin^2x)'+0=2\cos x\sin x=\sin 2x$
### 拉格朗日乘数法
对于一个函数 $f(x,y)$ 在附加条件 $\varphi(x,y)=0$ 下的极值,可以构造三元函数
$$L(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)$$
求解下面这个方程组,代回原方程就是他的极值点
$$\displaystyle\frac{\partial L}{\partial x}=0 \ \ \ \ \ \ \displaystyle\frac{\partial L}{\partial y}=0 \ \ \ \ \ \ \displaystyle\varphi(x,y)=0$$
例题 1. 已知 $x+y=1$,求 $x^2+y^2$ 的最值。
常规方法:$\displaystyle x^2+y^2=x^2+(1-x)^2=2x^2-2x+1\geq\frac{1}{2}$
拉格朗日乘数法:构造 $\varphi(x,y)=x+y-1\ \ \ \ \ f(x,y)=x^2+y^2$
$$L(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)=x^2+y^2+\lambda(x+y-1)$$
解方程
$$\displaystyle\frac{\partial L}{\partial x}=2x+\lambda=0 \ \ \ \ \ \ \displaystyle\frac{\partial L}{\partial y}=2y+\lambda=0 \ \ \ \ \ \ \displaystyle\varphi(x,y)=x+y-1=0$$
得到
$$x=\frac{1}{2}\ \ \ \ \ y=\frac{1}{2}\ \ \ \ \ \lambda=-1$$
最小值即 $\displaystyle f\left(\frac{1}{2},\frac{1}{2}\right)=\frac{1}{2}$.
例题 2. 已知 $a,b,c$ 均为正实数,$a^2+b^2+4c^2=1$,则 $ab+2ac+3\sqrt{2}bc$ 的最大值为 ?
$$\varphi(a,b,c)=a^2+b^2+4c^2-1\ \ \ \ \ f(a,b,c)=ab+2ac+3\sqrt{2}bc$$
$$L(a,b,c,\lambda)=ab+2ac+3\sqrt{2}bc+\lambda(a^2+b^2+4c^2-1)$$
$$\frac{\partial L}{\partial a}=b+2c+2a\lambda=0$$
$$\frac{\partial L}{\partial b}=a+3\sqrt{2}c+2b\lambda=0$$
$$\frac{\partial L}{\partial c}=2a+3\sqrt{2}b+8c\lambda=0$$
$$\varphi(a,b,c)=a^2+b^2+4c^2-1=0$$
解得
$$a=\frac{\sqrt{2}}{\sqrt{10}}\ \ \ \ b=\frac{2}{\sqrt{10}}\ \ \ \ c=\frac{1}{\sqrt{10}}\ \ \ \lambda=-\sqrt{2}$$
代回得到
$$f_{\max}=\sqrt{2}$$
练习 1. 将 $12$ 分为三个正整数 $x,y,z$ 之和,使得 $x^3y^2z$ 最大。( 答案:$x=6,y=4,z=2$ 时取最大值 $6912$ )
练习 2. 已知过定点 $(8,1)$ 的直线 $l$ 分别交 $x$ 轴正半轴于点 $A$,$y$ 轴负半轴于点 $B$,求 $|AB|$ 的最小值。
提示:设 $A(a,0),B(0,b)$ 代入得到 $\displaystyle\frac{8}{a}+\frac{1}{b}=1,|AB|^2=a^2+b^2$
答案:$a=10,b=5,|AB|_{\min}=5\sqrt{5}$
练习 3. 已知 $x^2+y^2+xy=1$,求 $x+y+xy$ 的最小值。
注意此处取等条件并非 $x=y$,答案是 $\displaystyle -\frac{5}{4}$,取等条件为 $\begin{cases} \displaystyle x+y=-\frac{1}{2} \\ \displaystyle xy=-\frac{3}{4} \end{cases}$
## 积分
为了保证高中生能看懂,这里的定积分知识非常有限。( 而且有点混乱 )
注意:如果你是 MOer,可忽略这部分内容,竞赛不考微积分。
### 几何意义
如果在 $[a,b](a\neq b)$ 上函数 $f(x)$ 连续且恒有 $f(x)\geq 0$,那么定积分 $\displaystyle\int_{a}^{b}f(x)dx$ 表示由曲线 $y=f(x)$ 以及直线 $x=a,x=b,y=0$ 围成的曲边梯形的面积。
若 $f(x)\leq 0$,那么定积分 $\displaystyle\int_{a}^{b}f(x)dx$ 表示由曲线 $y=f(x)$ 以及直线 $x=a,x=b,y=0$ 围成的曲边梯形的面积的**负值**。
如果我们把 $x$ 轴上方的面积赋予正号,下方的面积赋予负号,那么在一般情形下,定积分 $\displaystyle\int_{a}^{b}f(x)dx$ 表示由曲线 $y=f(x)$ 以及直线 $x=a,x=b,y=0$ 围成的各部分图形面积的代数和。
### 微积分基本定理 / $\mathrm{Newton-Leibniz}$ 牛顿 - 莱布尼兹公式
以下设 $C$ 是一个常数。
如果 $f(x)$ 是 $[a,b]$ 上的连续函数且 $F'(x)=f(x)$,那么
$$\boxed{\int_{a}^{b}f(x)\ dx=F(x)|_{a}^{b}=F(b)-F(a) }$$
我们称 $F(x)$ 是 $f(x)$ 的原函数。因为 $[F(x)+C]'=f(x)$,所以 $F(x)+C$ 也是 $f(x)$ 的原函数。
常用定积分公式:
$$\int_{a}^{b}C\ dx=Cx|_{a}^{b}=Cb-Ca=C(b-a)$$
$$\int_{a}^{b}x^n\ dx=\frac{1}{n+1}x^{n+1}|_{a}^{b}=\frac{1}{n+1}b^{n+1}-\frac{1}{n+1}a^{n+1}=\frac{b^{n+1}-a^{n+1} }{n+1}$$
$$\int_a^b\sin x\ dx=(-\cos x)|_a^b=-\cos b+\cos a$$
$$\int_a^b\cos x\ dx=\sin x|_a^b=\sin b-\sin a$$
$$\int_a^b\frac{1}{x}\ dx=\ln x|_a^b=\ln b-\ln a=\ln\frac{b}{a}$$
$$\int_a^b e^x\ dx=e^x|_a^b=e^b-e^a$$
$$\int_a^b n^x\ dx=\frac{n^x}{\ln n}|_a^b=\frac{n^b}{\ln b}-\frac{n^a}{\ln a}$$
$$\int_L^R \frac{cx+d}{ax+b}\ dx=\frac{cx}{a}+(\frac{d}{a}-\frac{bc}{a^2})\times\ln|ax+b|\ |_L^R$$
#### 定积分的基本性质
1. $$\int_a^b Cf(x)\ dx=C\int_a^b f(x)\ dx$$
2. $$\int_a^b[f(x)\pm g(x)]\ dx=\int_a^b f(x)\ dx\pm\int_a^b g(x)\ dx$$
3. $$\int_a^b f(x)\ dx=\int_a^c f(x)\ dx+\int_c^b f(x)\ dx$$
4. 在区间 $[a,b]$ 上满足 $f(x)\geq 0$,则 $$\int_a^b f(x)\ dx\geq 0$$
5. 在区间 $[a,b]$ 上满足 $f(x)\leq g(x)$,则 $$\int_a^b f(x)\ dx\leq\int_a^b g(x)\ dx$$
6. $$\left|\int_a^bf(x)\ dx\right |\leq\int_a^b|f(x)|\ dx$$
7. 若 $f(x)$ 是偶函数,且在 $[-a,a]$ 上连续,则 $$\int_{-a}^af(x)\ dx=2\int_0^af(x)\ dx$$
8. 若 $f(x)$ 是奇函数,且在 $[-a,a]$ 上连续,则 $$\int_{-a}^af(x)\ dx=0$$
#### 不定积分
我们现在需要一种简单的表示反导数的方式。根据微积分基本定理,我们可以用 $\displaystyle\int f(x)\ dx$ 表示 “ 函数 $f$ 的反导数的集合 ”,注意任何可积函数都有无数个反导数,唯一不同的是常数部分。例如,
$$\int x^2\ dx=\frac{x^3}{3}+C$$
对于任意常数 $C$ 都成立。也就是说,若 $F'(x)=f(x)$,则
$$\int f(x)\ dx=F(x)+C$$
不定积分的性质同定积分的性质。
#### 换元法
- 第一换元积分法:令 $y=g(x)$ 有:
$$\red{\boxed{\int_a^bf(g(x))g'(x)\ dx=\int_{g(a)}^{g(b)}f(y)\ dy}}$$
1. $$\int 2\sin 2x\ dx\xlongequal{u=2x}\int\sin u\ du=-\cos u+C=-\cos 2x+C\ \ \ \ (du=2dx)$$
2. $$\int (2x+1)^5\ dx\xlongequal{u=2x+1}\int u^5\ du=\frac{1}{12}u^6+C=\frac{1}{12}(2x+1)^6+C\ \ \ \ (du=2dx)$$
3. $$\begin{aligned}\int\frac{2x}{(x^2+1)^3}\ dx&=\int(x^2+1)^{-3}\cdot 2x\ dx\xlongequal{u=x^2+1}\int u^{-3}\ du\\&=-\frac{1}{2}u^{-2}+C=-\frac{1}{2(x^2+1)}+C\ \ \ \ (du=2xdx)\end{aligned}$$
4. $$\begin{aligned}\int x\sqrt{1-x^2}\ dx&=-\frac{1}{2}\int\sqrt{1-x^2}(-2x\ dx)\xlongequal{u=1-x^2}-\frac{1}{2}\int u^{\frac{1}{2}}\ du\\&=-\frac{1}{3}u^{\frac{3}{2}}+C=-\frac{1}{3}(1-x^2)^{\frac{3}{2}}+C\ \ \ \ (du=-2dx)\end{aligned}$$
5. $$\int\frac{1}{x^2+a^2}\ dx=\frac{1}{a^2}\int\frac{1}{\frac{x^2}{a^2}+1}\ dx=\frac{1}{a}\int\frac{1}{1+(\frac{x}{a})^2}\ d(\frac{x}{a})=\frac{1}{a}\arctan\frac{x}{a}+C$$
6. $$\int_0^1e^{2x}\ dx=\int_0^2\frac{1}{2}e^y\ dy=\frac{1}{2}(e^2-e^0)=\frac{1}{2}(e^2-1)$$
- 第二换元积分法:令 $x=g(t),dx=g'(t)dt$ 有:
$$\red{\boxed{\int f(x)\ dx=\int f[g(t)]g'(t)\ dt}}$$
1. $$\begin{aligned}\int\frac{1}{1+\sqrt x}\ dx&\xlongequal{x=t^2}\int\frac{1}{1+t}\cdot 2t\ dt=2\int(1-\frac{1}{1+t})\ dt=2t-2\ln|1+t|+C\\&=2\sqrt{x}-2\ln|1+\sqrt{x}|+C\end{aligned}$$
2. $$\begin{aligned}\int\sqrt{a^2-x^2}\ dx&\xlongequal{x=a\sin t}\int a\cos t\cdot a\cos t\ dt=a^2\int \cos^2 t\ dt\\&=a^2\int\frac{1+\cos 2t}{2}dt=a^2(\frac{1}{2}t+\frac{1}{4}\sin 2t)+C\\&=a^2(\frac{1}{2}\arcsin\frac{x}{a}+\frac{1}{4}\frac{2}{a^2}x\sqrt{a^2-x^2})+C\\&=\frac{a^2}{2}\arcsin\frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+C\end{aligned}$$
#### 分部积分法
$$(uv)'=u'v+uv'\implies uv'=(uv)'-vu'\implies \int uv'\ dx=uv-\int vu'\ dx$$
$$\red{\boxed{\int u\ dv=uv-\int v\ du}}$$
1. 计算 $\displaystyle\int x\cos x\ dx$,设 $u=x,dv=\cos x\ dx$,则 $du=dx,v=\sin x$
$$\int x\cos x\ dx=x\sin x-\int \sin x\ dx=x\sin x+\cos x+C$$
2. 计算 $\displaystyle\int\arctan x\ dx$,设 $u=\arctan x,dv=dx$,则 $\displaystyle du=\frac{1}{1+x^2}\ dx,v=x$
$$\begin{aligned}\int \arctan x&=x\arctan x-\int\frac{1}{1+x^2}\ dx=x\arctan x-\frac{1}{2}\int\frac{1}{1+x^2}d(1+x^2)\\&=x\arctan x-\frac{1}{2}\ln(1+x^2)+C\end{aligned}$$
3. 计算 $\displaystyle\int x\ln x\ dx$,设 $u=\ln x,dv=x\ dx$,则 $\displaystyle du=\frac{1}{x}\ dx,v=\frac{1}{2}x^2$
$$\int x\ln x\ dx=\frac{1}{2}x^2\ln x-\int\frac{1}{x}\cdot\frac{1}{2}x^2\ dx=\frac{1}{2}x^2\ln x-\frac{1}{4}x^2+C$$
#### Gamma 函数( 第二类欧拉积分 )
欧拉发现当 $n$ 为整数时,$\displaystyle\int_0^{+\infty}t^ne^{-t}\ dt=n!$,于是我们把 $n$ 替换成实数,就可变为
$$\Gamma(s)=\int_0^{+\infty}t^{s-1}e^{-t}\ dt$$
1. $s$ 为非正整数的复数 $s$ 时,$\Gamma(s+1)=s\Gamma(s)$
2. $n$ 为整数时,$\Gamma(n+1)=n!$
3. 余元公式( 欧拉反射原理 ):$s\in(0,1)$ 时,$\displaystyle\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin\pi s}$,得 $\displaystyle\Gamma\left(\frac{1}{2}\right)=\sqrt\pi$
#### 应用
1. 计算 $y=e^x$ 在 $x=0$ 与 $x=1$ 之间与 $x$ 轴围成的曲边梯形的面积。
只需计算 $\displaystyle\int_0^1e^x\ dx=e^1-e^0=e-1$
2. 计算 $x=y^2$ 与 $x=1$ 之间围成的图形的面积。
只需计算 $\displaystyle\int_0^1(\sqrt{x}-(-\sqrt{x}))\ dx=\int_0^1(2\sqrt{x})\ dx=\frac{4}{3}\sqrt{x^3}|_0^1=\frac{4}{3}-0=\frac{4}{3}$
3. 【2025 GD 一模 T19】如果函数 $F(x)$ 的导数为 $F'(x)=f(x)$,可记为 $\displaystyle\int f(x)\ dx=F(x)$,若 $f(x)\geq 0$,则 $\displaystyle\int_a^bf(x)\ dx=F(b)-F(a)$ 表示曲线 $y=f(x)$,直线 $x=a,x=b$ 以及 $x$ 轴围成的“曲边梯形”的面积。如:$\displaystyle\int 2x\ dx=x^2+C$,其中 $C$ 为常数;$\displaystyle\int_0^2 2x\ dx=(2^2+C)-(0+C)=4$,则表示 $x=0,x=1,y=2x+C$ 以及 $x$ 轴围成的面积为 $4$.
$(1)$ 若 $f(x)=\displaystyle\int(e^x+1)\ dx,f(0)=2$,求 $f(x)$ 的表达式。
$(2)$ 求曲线 $y=x^2$ 与直线 $y=-x+6$ 所围成图形的面积。
$(3)$ 若 $f(x)=e^x-1-2mx,x\in[0,+\infty)$,其中 $m\in\R,\forall a,b\in[0,+\infty)$,若 $a>b$,都满足 $\displaystyle\int_0^a f(x)\ dx>\int_0^b f(x)\ dx$,求 $m$ 取值范围。
解:$(1)\ f(x)=e^x+x+1$.
$(2)$ 先解方程 $x^2=-x+6$ 得到 $x=-3$ 或 $2$.
答案即为 $\displaystyle\int_{-3}^2 (-x+6-x^2)\ dx=(-\frac{1}{2}x^2+6x-\frac{1}{3}x^3)|_{-3}^2=\frac{22}{3}-(-\frac{27}{2})=\frac{125}{6}$.
$(3)$ 由题意可知,$\forall a,b\in[0,+\infty),a>b$ 满足 $F(a)-F(0)>F(b)-F(0)$,即 $F(a)\uparrow$,进而 $f(x)\geq 0$ 在 $[0,+\infty)$ 恒成立。
接下来就是常规导数了。分离参数 $m\leq\frac{e^x-1}{2x}=g(x),g'(x)=\frac{(x-1)e^x+1}{2x^2}$,令 $h(x)=(x-1)e^x,h'(x)=xe^x\geq 0$,即 $h(x)\uparrow,g'(x)\uparrow,g(x)\uparrow$,由洛必达法则,$\displaystyle m\leq\lim_{x\to 0}\frac{e^x-1}{2x}=\lim_{x\to 0}\frac{e^x}{2}=\frac{1}{2}$.
## 微积分在数列中的应用
秒杀神秘放缩的终极方法。但是需要一些高等知识,比如说解简单的常微分方程。但是一般的方程一眼看出来就可以了,这里给出通法:
对于一阶齐次线性微分方程:
$$y'+P(x)y=0$$
解为
$$y=Ce^{-\int P(x)dx}$$
对于一阶非齐次线性微分方程:
$$y'+P(x)y=Q(x)$$
先解 $y'+P(x)y=0$ 得到 $y=Ce^{-\int P(x)dx}$,再令 $C=u(x)$ 得
$$y=u(x)e^{-\int P(x) dx}$$
代入原方程得
$$u'(x)=\frac{Q(x)}{e^{-\int P(x)dx}}$$
对 $u'(x)$ 积分带入得到通解:
$$y=Ce^{-\int P(x)dx}+e^{-\int P(x)dx}\int Q(x)e^{\int P(x)dx}dx$$
以上的 $C$ 都为常数,由初始条件决定。
---
$\displaystyle a_1=1,a_{n+1}=a_n+\frac{1}{a_n}$,求 $a_{2024}$ 的整数部分 ?
设 $a_n$ 近似为一个连续函数 $f(x)$,考虑 $a_{n+1}-a_n$ 和 $\frac{1}{a_n}$ 的关系。对于 $n\to +\infty$,有
$$f'(x)=\frac{1}{f(x)}\implies\frac{\mathrm{d}f(x)}{\mathrm{d}x}=\frac{1}{f(x)} \implies f(x)\mathrm{d}f(x)=\mathrm{d}x\\\implies\int f(x)\mathrm{d}f(x)=\int\mathrm{d}x\implies \frac{f^2(x)}{2}=x+C$$
由 $f(1)=1$ 得到 $\displaystyle C=-\frac{1}{2}$,微分方程解得 $f(x)=\sqrt{2x-1}$,得到 $f(2024)=\sqrt{4047}\approx 63$
---
已知 $\displaystyle a_1=1,a_{n+1}=a_n-\frac{1}{3}a_n^2$,则 $100a_{100}$ 的范围是哪个:$\displaystyle\left(2,\frac{5}{2}\right),\left(\frac{5}{2},3\right), \left(3,\frac{7}{2}\right)$ ?
$$\frac{1}{a_{n+1}}=\frac{3}{a_n(3-a_n)}=\frac{1}{a_n}+\frac{1}{3-a_n}>\frac{1}{a_n}+\frac{1}{3}$$
$$\frac{1}{a_n}>a_1+\frac{n-1}{3}=\frac{n+2}{3}\implies a_n<\frac{3}{n+2}\implies 100a_{100}<3$$
$$\frac{1}{a_{n+1}}<\frac{1}{a_n}+\frac{1}{3-\frac{3}{n+2}}=\frac{1}{a_n}+\frac{n+2}{3(n+1)}=\frac{1}{a_n}+\frac{1}{3}+\frac{1}{3(n+1)}$$
$$\frac{1}{a_{100}}<\frac{1}{a_1}+\frac{99}{3}+\frac{1}{3}\left(\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{100}\right)=34+\frac{1}{3}\left(\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{100}\right)$$
**注意到**
$$\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{100}<\frac{1}{2}\times 4+\frac{1}{6}\times 96=18$$
$$\frac{1}{a_{100}}<\frac{1}{40}\implies 100a_{100}>\frac{5}{2}$$
这道题是我们班的补充题,当时无人证出 $\displaystyle >\frac{5}{2}$,我们老师上课思考了不到 $15$ 分钟讲了这种方法( 他从不备课 ),注意力简直惊为天人。
积分法:$\displaystyle f(x)=a_n,f'(x)=\frac{df(x)}{dx}=-\frac{1}{3}f^2(x)\implies \int f^{-2}(x)df(x)=\int-\frac{1}{3}dx\\-f^{-1}(x)=-\frac{1}{3}x+C,f(x)=\frac{3}{x+C}\implies\frac{3}{x+2}$,显然 $\displaystyle 100a_{100}\in\left(\frac{5}{2},3\right)$. 可以代入 $a_2,a_3$ 获得更高的精度。
<!-- 已知 $\displaystyle a_1=1,a_{n+1}=\frac{a_n}{1+\sqrt{a_n}}$,求 $S_{100}$ 的整数部分。
$$\frac{1}{a_{n+1}}=\frac{1}{a_n}+\frac{1}{\sqrt{a_n}}\xlongequal{b_n=\frac{1}{a_n}}b_{n+1}=b_n+\sqrt{b_n}\xlongequal{f(x)=b_n}f'(x)=f^{\frac{1}{2}}(x)\\ \int f^{-\frac{1}{2}}(x)df(x)=\int dx\implies 2f^{\frac{1}{2}}(x)=x+C\implies f(x)=\left(\frac{x+C}{2}\right)^2\\b_n=\left(\frac{n+1}{2}\right)^2,a_n=\frac{4}{(n+1)^2},\sum_{n=2}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}-1\implies S_{\infty}=4\left(\frac{\pi^2}{6}-1\right)\approx 2.58$$ -->
---
已知 $\displaystyle a_1=1,a_{n+1}=\frac{a_n}{1+\sqrt[3]{a_n}}$,求 $S_{100}$ 的整数部分。
答案:准确值是 $2.38$.
$$\frac{1}{a_{n+1}}=\frac{1}{a_n}+\frac{1}{a_n^{\frac{2}{3}}}\xlongequal{b_n=\frac{1}{a_n}}b_{n+1}=b_n+b_n^{\frac{2}{3}}\xlongequal{f(x)=b_n}f'(x)=f^{\frac{2}{3}}(x)$$
$$\int f^{-\frac{2}{3}}(x) df(x)=\int dx\implies 3f^{\frac{1}{3}}(x)=x+C\implies f(x)=\left(\frac{x+2}{3}\right)^3=\left(\frac{x-2+3\sqrt[3]{2}}{3}\right)^3$$
$$a_n=\frac{27}{(x+2)^3},\zeta(3)=\sum_{n=1}^{\infty}\frac{1}{n^3}\approx 1.202,S_{\infty}=27\cdot 0.077=2.079$$
另外,欧拉常数 $\displaystyle\gamma=\lim_{n\to\infty}\left[\left(\sum_{k=1}^n\frac{1}{k}\right)-\ln n\right]=\int_1^{\infty}\left(\frac{1}{\lfloor x\rfloor}-\frac{1}{x}\right)\approx 0.57721 56649 01532 86060$,于是可以估计 $\displaystyle\sum_{k=1}^n\frac{1}{k}\approx\ln n+\gamma$.
---
也可以用一个结论( Basel 问题,[here](https://zhuanlan.zhihu.com/p/144278965) ):$\red{\boxed{\sum_{n=1}^{+\infty}\frac{1}{n^2}=\frac{\pi^2}{6}\approx 1.645}}$
相关证明:设黎曼 Zeta 函数 $\zeta(s)=\displaystyle\sum_{n=1}^{+\infty}\frac{1}{n^s}\ (s>1)$,显然 $\displaystyle\lim_{s\to 1^+}\zeta(s)=+\infty,\lim_{s\to+\infty}\zeta(s)=1$.
由泰勒展开得 $\displaystyle\sin x=x-\frac{x^3}{6}+\frac{x^5}{120}+\dots=\sum_{k=0}^{+\infty}\frac{(-1)^k}{(2k+1)!}x^{2k+1}$
因此 $\displaystyle\frac{\sin x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}+\dots=\sum_{n=0}^{+\infty}\frac{(-1)^nx^{2n}}{(2n+1)!}①$( $\displaystyle\frac{\sin x}{x}$ 的无穷级数展开 )
熟知 $\displaystyle\frac{\sin x}{x}$ 的无穷乘积展开 $\displaystyle\frac{\sin x}{x}=\prod_{n=1}^{+\infty}\left(1-\frac{x^2}{n^2\pi^2}\right)=\left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\cdots②$
Basel 问题即 $\displaystyle\zeta(2)=\sum_{n=1}^{+\infty}\frac{1}{n^2}$,比较 $①②$ 式中二次项系数得 $\displaystyle -\frac{1}{3!}=-\frac{1}{\pi^2}-\frac{1}{2^2\pi^2}-\dots$
由此可得 $\displaystyle\zeta(2)=\frac{\pi^2}{6}$,进一步地我们有 $\displaystyle\zeta(4)=\frac{\pi^4}{90},\zeta(6)=\frac{\pi^6}{945}$.
$$\zeta(2n)=\left[\sum_{k=1}^{n-1}\frac{(-1)^{k+1}\pi^{2k}\zeta(2n-2k)}{(2k+1)!}\right]+\frac{(-1)^{n+1}n\pi^{2n}}{(2n+1)!}\ \ \ \ \ \ n\in\N^*$$
上述思路可总结出一个结论:若 $\displaystyle\sum_{k=0}^{+\infty}a_kx^k=\prod_{k=1}^{+\infty}(1+b_kx)$,设 $S_n=\displaystyle\sum_{k=1}^{+\infty}b_k^n$,则 $$S_1=a_1,\ \ \ S_n=\displaystyle\sum_{k=1}^{n-1}(-1)^{k+1}a_kS_{n-k}+(-1)^{n+1}na_n$$
#### 积分放缩在数列中的应用
我们熟知的积分放缩一般是这样的( 证明:几何意义 )
$$\int_1^{n+1}f(x)\ dx <\sum_{k=1}^nf(k)<\int_0^nf(x)\ dx\ \ \ \ \ \ \ \ f(x)\downarrow$$
$$\int_0 ^{n}f(x)\ dx<\sum_{k=1}^nf(k)<\int_1^{n+1}f(x)\ dx\ \ \ \ \ \ \ \ f(x)\uparrow$$
例如:
$$\begin{aligned}\sum_{k=1}^n\frac{1}{\sqrt{k} }&>\int_1^{n+1}\frac{1}{\sqrt{x} }\ dx=2\sqrt{x}|_1^{n+1}=2\left(\sqrt{n+1}-1\right)\\&<\int_0^n\frac{1}{\sqrt{x} }\ dx=2\sqrt{x}|_0^n=2\sqrt{n}\end{aligned}$$
练习 1:证明 $\displaystyle\sum_{k=2}^n\frac{1}{k\sqrt{k}}<\sqrt{2}\ \ \ \ \text{}$ 和 $\ \ \ \ \displaystyle\frac{2}{3}n^\frac{3}{2}\leq\sum_{k=1}^n\sqrt{k}\leq\frac{2}{3}[(n+1)^\frac{3}{2}-n]$
练习 2:证明 $\displaystyle\sum_{k=2}^{n+1}\frac{1}{k}<\ln(n+1)<\sum_{k=1}^n\frac{1}{k}\ \ \ \ \text{}$ 和 $\ \ \ \ \displaystyle\frac{4}{7}<\sum_{k=n+1}^{2n}\frac{1}{k}<\ln 2<\frac{25}{36}<\frac{\sqrt{2}}{2}$
练习 3:证明 $\displaystyle\begin{cases}\displaystyle\sum_{k=1}^n\frac{1}{k^p}<\frac{p}{p-1}&p>1\\\displaystyle\sum_{k=1}^n\frac{1}{k^p}\geq\displaystyle\sum_{k=1}^n\frac{1}{k}>\ln n&p\leq 1\end{cases}$
我们还可以根据 $f(x)$ 的凹凸性进一步放缩。
当 $f(x)\downarrow$ 且下凸时,
$$\int_1^{n+1}f(x)\ dx+\frac{f(1)-f(n+1)}{2}<\sum_{k=1}^nf(k)<\int_0^nf(x)\ dx$$
当 $f(x)\downarrow$ 且上凸时,
$$\int_1^{n+1}f(x)\ dx<\sum_{k=1}^nf(k)<\int_0^nf(x)\ dx-\frac{f(0)-f(n)}{2}$$
当 $f(x)\uparrow$ 且下凸时,
$$\int_0^nf(x)\ dx+\frac{f(n)-f(0)}{2}<\sum_{k=1}^nf(k)<\int_1^{n+1}f(x)\ dx$$
当 $f(x)\uparrow$ 且上凸时,
$$\int_0^nf(x)\ dx<\sum_{k=1}^nf(k)<\int_1^{n+1}f(x)\ dx-\frac{f(n+1)-f(1)}{2}$$
## 生成函数 / 母函数
序列 $a$ ( 有穷无穷均可 )的普通生成函数定义为形式幂级数:$\displaystyle F(x)=\sum_na_nx^n$。例如:
1. $a=\lang1,2,3\rang$ 的普通生成函数是 $1+2x+3x^2$
2. $a=\lang1,1,1,\dots\rang$ 的普通生成函数是 $\displaystyle\sum_{n\geq 0}x^n$
3. $a=\lang1,2,4,8,16,\dots\rang$ 的生成函数是 $\displaystyle\sum_{n\geq 0}2^nx^n$
4. $a=\lang1,3,5,7,9\rang$ 的生成函数是 $\displaystyle\sum_{n\geq 0}(2n+1)x^n$
换句话说,如果序列 $a$ 有通项公式,那么它的普通生成函数的系数就是通项公式。
#### 基本运算
两个序列 $a,b$ 的生成函数 $F(x),G(x)$,则 $F(x)\pm G(x)$ 是序列 $\lang a_n\pm b_n\rang$ 的生成函数。
$$F(x)\pm G(x)=\sum_{n}(a_n\pm b_n)x^n$$
乘法运算即卷积,推出 $F(x)G(x)$ 是序列 $\left\lang\displaystyle\sum_{i=0}^na_ib_{n-i}\right\rang$ 的生成函数。
$$F(x)G(x)=\sum_nx^n\sum_{i=0}^na_ib_{n-i}$$
#### 形式幂级数形式 $\to$ 封闭形式
例如 $a=\lang1,1,1,\dots\rang$ 的普通生成函数是 $\displaystyle F(x)=\sum_{n\geq 0}x^n$,可以发现 $F(x)x+1=F(x)$,于是解方程得到 $\displaystyle F(x)=\frac{1}{1-x}$,这就是 $\displaystyle\sum_{n\geq 0}x^n$ 的封闭形式。
又例如等比数列 $\lang1,p,p^2,\dots\rang$ 的生成函数 $F(x)=\displaystyle\sum_{n\geq 0}p^nx^n$,有 $F(x)px+1=F(x)$ 得 $F(x)=\displaystyle\frac{1}{1-px}$.
$a=\lang 1,0,1,0,1,\dots\rang$ 的 $F(x)=\displaystyle\sum_{n\geq 0}x^{2n}=\frac{1}{1-x^2}$
$a=\lang 1,2,3,4,\dots\rang$ 的 $F(x)=\displaystyle\sum_{n\geq 0}(n+1)x^n=\sum_{n\geq 0}(x^n)'=\left(\frac{1}{1-x}\right)'=\frac{1}{(1-x)^2}$
$a_n=\begin{pmatrix}m\\n\end{pmatrix}$ 的 $F(x)=\displaystyle\sum_{n\geq 0}\begin{pmatrix}m\\n\end{pmatrix}x^n=(1+x)^m$
$Fib$ 数列定义为 $a_0=0,a_1=1,a_n=a_{n-1}+a_{n-2}$,于是有
$$F(x)=xF(x)+x^2F(x)-a_0x+a_1x+a_0\implies F(x)=\frac{x}{1-x-x^2}$$
#### 应用
1. 在许多不同种类的食物中选出 $n$ 个,计算方案数。每种食物的限制如下:
| 汉堡:偶数个 | 可乐:不超高一个 | 鸡腿:不超过两个 | 蜜桃多:奇数个 |
|:-:|:-:|:-:|:-:|
| 鸡块:$4$ 的倍数个 | 包子:不超过三个 | 土豆片炒肉:不超过一个 | 面包:$3$ 的倍数个 |
构造生成函数:
| $\displaystyle\sum_{n\geq 0}x^{2n}=\frac{1}{1-x^2}$ | $1+x$ | $\displaystyle 1+x+x^2=\frac{1-x^3}{1-x}$ | $\displaystyle\frac{x}{1-x^2}$ |
|:-:|:-:|:-:|:-:|
| $\displaystyle\sum_{n\geq 0}x^{4n}=\frac{1}{1-x^4}$ | $\displaystyle 1+x+x^2+x^3=\frac{1-x^4}{1-x}$ | $1+x$ | $\displaystyle\frac{1}{1-x^3}$ |
全部乘起来得到答案的生成函数:
$$F(x)=\frac{(1+x)(1-x^3)x(1-x^4)(1+x)}{(1-x^2)(1-x)(1-x^2)(1-x^4)(1-x)(1-x^3)}=\frac{x}{(1-x)^4}=\sum_{n\geq 1}\begin{pmatrix}n+2\\n-1\end{pmatrix}x^n$$
于是答案 $=\begin{pmatrix}n+2\\n-1\end{pmatrix}=\begin{pmatrix}n+2\\3\end{pmatrix}$
2. $a_{n+1}+a_n=2^n,a_0=0$,求通项。
$f(x)=\displaystyle\sum_{n=0}^{+\infty}a_nx^n$,原式变为 $x^{-1}(a_{n+1}x^{n+1})+a_nx^n=(2x)^n$,再求和有
$$\displaystyle\sum_{n=0}^{+\infty}x^{-1}(a_{n+1}x^{n+1})+\sum_{n=0}^{+\infty}(a_nx^n)=\sum_{n=0}^{+\infty}(2x)^n=\frac{1}{1-2x}\implies (\frac{1}{x}+1)f(x)=\frac{1}{1-2x}$$
$$f(x)=\frac{x}{(1-2x)(1+x)}=\frac{1}{3}(\frac{1}{1-2x}-\frac{1}{1+x})=\frac{1}{3}\sum_{n=0}^{+\infty}[2^n-(-1)^n]x^n$$
于是 $\displaystyle a_n=\frac{1}{3}[2^n-(-1)^n]$.
3. 卡特兰数:一个 $n\times n$ 的方阵从 $(0,0)$ 走到 $(n,n)$,不经过对角线的方案数,记作 $C_n$。
有如下关系:$C_n=\displaystyle\sum_{k=0}^nC_{n-k}C_k$,构造 $f(x)=\displaystyle\sum_{n=0}^{+\infty}C_nx^n$,有
$$f^2(x)=C_0^2+(C_0C_1+C_1C_0)x+\dots\implies xf^2(x)+C_0=f(x)\implies f(x)=\frac{1-\sqrt{1-4x} }{2x}$$
$$\implies f(x)=\frac{1-\left\{1+\displaystyle\sum_{k=1}^{+\infty}\left[-2\begin{pmatrix}2k-2\\ k-1\end{pmatrix}\right]x^k\right\}}{2x}=\sum_{k=0}^{+\infty}\frac{\begin{pmatrix}2k\\k\end{pmatrix}x^k}{k+1}\implies\red{\boxed{C_n=\frac{\begin{pmatrix}2n\\n\end{pmatrix}}{n+1}}}$$
## $\mathrm{Stolz}$ 定理( 数列中的洛必达法则 )
设数列 $\set{b_n}$ 单调递**增**且 $\displaystyle\lim_{n\to+\infty}b_n=+\infty$,或者$\set{b_n}$ 单调递**减**且 $\displaystyle\lim_{n\to+\infty}b_n=0$。如果 $\displaystyle\lim_{n\to+\infty}\frac{a_n-a_{n-1}}{b_n-b_{n-1}}$ 存在或为 $\pm\infty$,则
$$\lim_{n\to+\infty}\frac{a_n}{b_n}=\lim_{n\to+\infty}\frac{a_n-a_{n-1}}{b_n-b_{n-1}}$$
1. $\displaystyle\lim_{n\to+\infty}\sqrt[n]{n}=e^{\lim_{n\to\infty}\frac{\ln n}{n}}=e^{\lim_{n\to\infty}\frac{\ln\frac{n}{n-1}}{1}}=1$
2. $\displaystyle\lim_{n\to+\infty}\frac{\sum_{x=1}^n\sqrt{x}}{n\sqrt{n}}=\lim_{n\to+\infty}\frac{\sqrt n}{n^{\frac{3}{2}}-(n-1)^{\frac{3}{2}}}=\lim_{n\to+\infty}\frac{n^2+(n-1)\sqrt{n^2-n}}{3n^2-3n+1}=\frac{2}{3}$
3. 证明:当 $n\geq 2$ 时,$\displaystyle\ln\left(\frac{n+1}{2}\right)<1+\frac{1}{2}+\dots+\frac{1}{n-1}$
只需证 $\displaystyle\frac{1+\frac{1}{2}+\dots+\frac{1}{n-1}}{\ln(\frac{n+1}{2})}>1$,因为 $LHS$ 增长速度 $>RHS$,所以只需证
$$\lim_{n\to+\infty}\frac{1+\frac{1}{2}+\dots+\frac{1}{n-1}}{\ln(\frac{n+1}{2})}\leq 1$$
而因为当 $n\to+\infty$ 时,$\ln(\frac{n+1}{n})$ 与 $\frac{1}{n}$ 等价无穷小,所以
$$\lim_{n\to+\infty}\frac{1+\frac{1}{2}+\dots+\frac{1}{n-1}}{\ln(\frac{n+1}{2})}=\lim_{n\to+\infty}\frac{\frac{1}{n-1}}{\ln(\frac{n+1}{n})}=\lim_{n\to+\infty}\frac{\frac{1}{n-1}}{\frac{1}{n}}<1$$
写的时候这样写:因为 $\displaystyle\ln\left(1+\frac{1}{n}\right)<\frac{1}{n}$,对左右两边求和即可。( 倒推 )
练习:证明 $\displaystyle n>1,\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n}<\ln n$.
# 应试要求
- 强制开根号:$\displaystyle\red{\boxed{\sqrt{a\pm\sqrt{b}}=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}\pm\sqrt{\frac{a-\sqrt{a^2-b}}{2}}}}$
例如:$\displaystyle\sqrt{3-2\sqrt{2}}=\sqrt{3-\sqrt{8}}=\sqrt{\frac{3+1}{2}}-\sqrt{\frac{3-1}{2}}=\sqrt{2}-1$
- 方程两边同除一个数要写明这个数 $\neq 0$,求 $f(x)\neq 0$ 的解集用 **"且"** 连接,如求 $x^2-2x-3\neq 0$ 的解集 $\implies x\neq 3$ 且 $x\neq -1$.
- 保留 $n$ 位有效数字:从左到右读到第一个不为 $0$ 的数位后向后继续读 $(n-1)$ 位并四舍五入。
如对 $0.0168$ 保留 $2$ 位有效数字:$0.017$
- 分类讨论:最后要写“综上所述”。
- 集合:考虑**空集**,条件注意是否有写 “**不充分**” “**不必要**” 等字眼
- 不等式:**写明取等条件**,例如 $(x=\dots,y=\dots)$.
- 函数:通过奇偶性求函数解析式需 **检验**;写出单调区间时用 **$,$** 不用 **$\bigcup$**.
比如 "$y=\sin x$ 在第二象限为减函数 " 是错误的,因为第二象限相当于很多个区间取并,即 $(\ \ )\bigcup(\ \ )\bigcup...\bigcup(\ \ )$,而表示单调性不能用 $\bigcup$.
求出函数表达式需写**定义域**,并且必须化至最简。
- 第 一/二/三/四 象限均**不包括** 坐标轴。
- 使用 $\displaystyle A\sin\alpha+B\cos\alpha=\sqrt{A^2+B^2}\sin\left(\alpha+\arctan{\frac{B}{A}}\right)$ 需写详细过程,不可跳步。
**$\displaystyle\frac{B}{A}<0$ 时,最好检验 $\varphi$ 位于第二象限还是第四象限**。
- 作图题:**列表**描点,曲线自然,直尺。
- 应用题:求出函数表达式需写**定义域**,分类讨论取最大值或最小值时需写明 $\because A>B \ \therefore 选A$.
如 $f(\sqrt{x}+1)=x-2$,求 $f(x)=x^2-2x-1\ 且\ x\in [1,+\infty)$
- 向量:$|\mathbf{t}|=\sqrt{\mathbf{t}^2}$;注意向量共线( 正向 or 反向 )的情况;回答时写明 **大小+方向**;几何法不行 $\to$ **建系**;注意与三角函数结合( 三角换元,出现动点注意坐标用三角函数表示... );利用初中技巧( 倍长中线 )。
若已知 $\mathbf{a}=(1,2)$,则任意平移 $\mathbf{a}$ 得到 $\mathbf{b}$,因为模长不变,所以 $\mathbf{b}=(1,2)$.
- 解三角形:写明 **"在...三角形中""由正 / 余弦定理得"**;已知 $\Delta ABC$ 先写 $A\in(0,\pi)$,再写 $A=...\degree$
注意:已知 $\sin x=\sin y$,则有两种情况:$x=y$ 或 $x=\pi -y$.
- 立体几何:在棱柱( 包括长方体,正方体等 )中证明时,只能使用直棱柱的侧棱互相平行且相等这一性质,其余均需证明。
在空间中,不能用两组对边分别相等证明平行四边形。
- 统计:记得写 $H_0$ 零假设,并且注意极小概率值 $\alpha$ 的表达。
- 概率:要写明 $A,B,\dots$ 是互斥事件 / 对立事件等。枚举时要写明有序 / 无序,有序用 $(A,B)$,无序用 $AB$。记 $\dots$ 为 $x_1,x_2$,则样本点为 $(x_1,x_2)$。
- 解析几何:讨论**斜率存在/不存在**,联立之后算 $\Delta>0$. 不确定焦点是在 $x$ 轴上还是在 $y$ 轴上要分类讨论。有时候利用第二第三定义可以简化很多计算。
- 数列:注意 $n=1$ 是否满足你推出来的式子。善用数学归纳法,没证出来是没分的。等差数列的公差可以为 $0$,等比数列的公比可以为 $\pm 1$,不可以为 $0$.
- 导数:最好列表判断单调性;令导数值等于 $0$ 要写在分类之后( 定义域问题 );不能直接 $f''(x),f'''(x)\dots$,要另外设一个新函数再求二阶导、三阶导……
- 能否使用洛必达法则:我们老师说可以,但是不能显式地写出。直接写 $\displaystyle\lim_{x\to a}f(x)=\dots$ 即可,别写“根据洛必达法则”。这个可能不同地区不同要求,最好询问老师。
相关推荐
评论
共 234 条评论,欢迎与作者交流。
正在加载评论...