专栏文章

主定理学习笔记

xxiaoniu142857
算法·理论参与者 8已保存评论 10

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
10 条
当前快照
1 份
快照标识符
@mlia5xn3
此快照首次捕获于
2026/02/12 01:05
上周
此快照最后确认于
2026/02/19 01:14
14 小时前
查看原文
主定理（Master Theorem）是用于分析分治算法复杂度的重要定理。

前置知识

渐进符号的概念

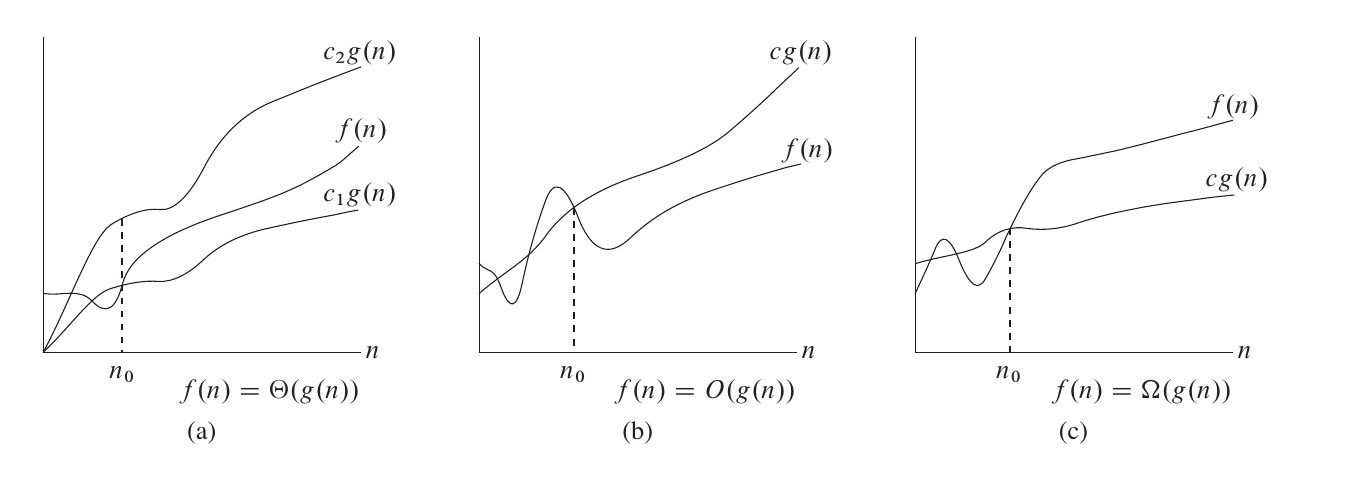
1. Θ\mathcal{\Theta}（紧确渐进界）

若存在正常数 c1,c2,n0c_1,c_2,n_0 使得 ∀n≥n0\forall n\ge n_0 都有：
0≤c1⋅g(n)≤f(n)≤c2⋅g(n)0\le c_1\cdot g(n)\le f(n)\le c_2\cdot g(n)
则记 f(n)=Θ(g(n))f(n)=\mathcal{\Theta}(g(n))。Θ\mathcal{\Theta} 是等价关系，表示 f,gf,g 增长速度同阶，类似 ==。

2. O\mathcal{O}（渐进上界）

若存在正常数 c,n0c,n_0 使得 ∀n≥n0\forall n\ge n_0 都有：
0≤f(n)≤c⋅g(n)0\le f(n)\le c\cdot g(n)
则记 f(n)=O(g(n))f(n)=\mathcal{O}(g(n))。O\mathcal{O} 是拟序关系，类似 ≤\le（小于等于）。

3. Ω\mathcal{\Omega}（渐进下界）

若存在正常数 c,n0c,n_0 使得 ∀n≥n0\forall n\ge n_0 都有：
0≤c⋅g(n)≤f(n)0\le c\cdot g(n)\le f(n)
则记 f(n)=Ω(g(n))f(n)=\mathcal{\Omega}(g(n))。Ω\mathcal{\Omega} 也是拟序关系，类似 ≥\ge（大于等于）。
三者如下图所示。

常用性质

  1. f(n)=Θ(g(n))⇔f(n)=O(g(n))∧f(n)=Ω(g(n))f(n)=\mathcal{\Theta}(g(n))\Leftrightarrow f(n)=\mathcal{O}(g(n)) \land f(n)=\mathcal{\Omega}(g(n))
  2. f(n)=Θ(f(n))f(n)=\mathcal{\Theta}(f(n))
  3. c⋅Θ(f(n))=Θ(f(n))c\cdot \mathcal{\Theta}(f(n))=\mathcal{\Theta}(f(n))（c>0c>0 且 cc 与 nn 无关）
  4. Θ(f(n))+Θ(g(n))=Θ(f(n)+g(n))=Θ(max⁡(f(n),g(n)))\mathcal{\Theta}(f(n))+\mathcal{\Theta}(g(n))=\mathcal{\Theta}(f(n)+g(n))=\mathcal{\Theta}(\max(f(n),g(n)))
  5. Θ(f(n))Θ(g(n))=Θ(f(n)g(n))\mathcal{\Theta}(f(n))\mathcal{\Theta}(g(n))=\mathcal{\Theta}(f(n)g(n))
  6. Θ(log⁡bn)=Θ(log⁡2n)\mathcal{\Theta}(\log_b n)=\mathcal{\Theta}(\log_2 n)（b>1b>1）
性质 2~6 同样适用于 O\mathcal{O} 和 Ω\mathcal{\Omega}。
这些性质会在后面的证明中用到。

主定理简化版

设 T(n)T\left(n\right) 为分治算法处理规模为 nn 的问题的复杂度，且满足：
T(n)={aT(nb)+Θ(nd)if  n≥bΘ(1)if  n<bT\left(n\right)= \begin{cases} aT\left(\frac{n}{b}\right)+\mathcal{\Theta}\left(n^d\right) & \text{if}\;n\ge b\\ \mathcal{\Theta}\left(1\right) & \text{if}\;n<b \end{cases}
其中：
  • aa：子问题个数（a∈Z,a≥1a\in \mathbb{Z},a\ge 1）。
  • nb\frac{n}{b}：每个子问题大小（b∈R,b>1b\in \mathbb{R},b>1）。
  • Θ(nd)\mathcal{\Theta}\left(n^d\right)：合并子问题的解得到原问题解的额外复杂度（d≥0d\ge 0）。
则有：
T(n)={Θ(nlog⁡ba)if  d<log⁡baΘ(ndlog⁡n)if  d=log⁡baΘ(nd)if  d>log⁡baT\left(n\right)=\begin{cases} \mathcal{\Theta}\left(n^{\log_b a}\right) & \text{if} \; d<\log_b a \\ \mathcal{\Theta}\left(n^d \log n\right) & \text{if} \; d=\log_b a \\ \mathcal{\Theta}\left(n^d\right) & \text{if} \; d>\log_b a \end{cases}
Θ\mathcal{\Theta} 也可以替换成 O,Ω \mathcal{O,\Omega}。
这对于 OI 来说已经够用了。

例子

  • 对于归并排序，a=2,b=2,d=1a=2,b=2,d=1，有 d=log⁡bad=\log_ba，因此时间复杂度为 Θ(nlog⁡n)\Theta(n\log n)。
  • 对于 a=2,b=2,d=2a=2,b=2,d=2 的完全二叉树上背包问题，有 d>log⁡bad>\log_ba，因此时间复杂度为 Θ(n2)\Theta(n^2)。

证明

不失一般性地，假设 nn 是 bb 的整数次幂。
考虑递归树。若根节点算一层，则树高为 log⁡bn+1\log_b n+1。单独计算叶子节点，展开得：
T(n)=Θ(alog⁡bn)+∑k=0log⁡bn−1ak⋅Θ((nbk)d)=Θ(alog⁡bn)+∑k=0log⁡bn−1Θ(ak)⋅Θ((nbk)d)=Θ(nlog⁡ba)+∑k=0log⁡bn−1Θ(ak⋅nd(bd)k)=Θ(nlog⁡ba)+∑k=0log⁡bn−1Θ((abd)k⋅nd)=Θ(nlog⁡ba)+Θ(∑k=0log⁡bn−1(abd)k⋅nd)=Θ(nlog⁡ba)+Θ(nd⋅∑k=0log⁡bn−1(abd)k)\begin{aligned} T\left(n\right)&=\mathcal{\Theta}\left(a^{\log_bn}\right)+\sum_{k=0}^{\log_b n-1}a^k\cdot \mathcal{\Theta}\left(\left(\frac{n}{b^k}\right)^d\right)\\ &=\mathcal{\Theta}\left(a^{\log_bn}\right)+\sum_{k=0}^{\log_b n-1}\mathcal{\Theta}\left(a^k\right)\cdot \mathcal{\Theta}\left(\left(\frac{n}{b^k}\right)^d\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\sum_{k=0}^{\log_b n-1}\mathcal{\Theta}\left(a^k\cdot \frac{n^d}{\left(b^d\right)^k}\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\sum_{k=0}^{\log_b n-1}\mathcal{\Theta}\left(\left(\frac{a}{b^d}\right)^k\cdot n^d\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(\sum_{k=0}^{\log_b n-1}\left(\frac{a}{b^d}\right)^k\cdot n^d\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot\sum_{k=0}^{\log_b n-1}\left(\frac{a}{b^d}\right)^k\right)\\ \end{aligned}
设 p=abdp=\frac{a}{b^d}，则：
{p>1if  d<log⁡bap=1if  d=log⁡ba0<p<1if  d>log⁡ba\begin{cases} p>1 & \text{if} \; d<\log_ba \\ p=1 & \text{if} \; d=\log_ba \\ 0<p<1 & \text{if} \; d>\log_ba \\ \end{cases}
且
T(n)=Θ(nlog⁡ba)+Θ(nd⋅∑k=0log⁡bn−1pk)T\left(n\right)=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot\sum_{k=0}^{\log_b n-1}p^k\right)

情况 1（d<log⁡bad<\log_ba）

此时 p>1p>1。
由等比数列求和公式，得：
T(n)=Θ(nlog⁡ba)+Θ(nd⋅plog⁡bn−1p−1)=Θ(nlog⁡ba)+Θ(nd⋅(plog⁡bn−1))=Θ(nlog⁡ba)+Θ(nd⋅((abd)log⁡bn−1))=Θ(nlog⁡ba)+Θ(nd⋅(alog⁡bnbdlog⁡bn−1))=Θ(nlog⁡ba)+Θ(nd⋅(nlog⁡band−1))=Θ(nlog⁡ba)+Θ(nlog⁡ba−nd)=Θ(nlog⁡ba)\begin{aligned} T\left(n\right)&=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \frac{p^{\log_bn}-1}{p-1}\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \left(p^{\log_bn}-1\right)\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \left(\left(\frac{a}{b^d}\right)^{\log_bn}-1\right)\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \left(\frac{a^{\log_bn}}{b^{d\log_bn}}-1\right)\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot\left(\frac{n^{\log_b a}}{n^d}-1\right)\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^{\log_b a}-n^d\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right) \end{aligned}

情况 2（d=log⁡bad=\log_ba）

此时 p=1p=1。
T(n)=Θ(nlog⁡ba)+Θ(nd⋅log⁡bn)=Θ(nlog⁡ba)+Θ(ndlog⁡n)=Θ(ndlog⁡n)\begin{aligned} T\left(n\right)&=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \log_bn\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\log n\right)\\ &=\mathcal{\Theta}\left(n^d\log n\right) \end{aligned}

情况 3（d>log⁡bad>\log_ba）

此时 0<p<10<p<1。
由等比数列求和公式，得：
T(n)=Θ(nlog⁡ba)+Θ(nd⋅plog⁡bn−1p−1)=Θ(nlog⁡ba)+Θ(nd⋅1−plog⁡bn1−p)=Θ(nlog⁡ba)+Θ(nd)⋅Θ(1)=Θ(nd)\begin{aligned} T\left(n\right)&=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \frac{p^{\log_bn}-1}{p-1}\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\cdot \frac{1-p^{\log_bn}}{1-p}\right)\\ &=\mathcal{\Theta}\left(n^{\log_ba}\right)+\mathcal{\Theta}\left(n^d\right)\cdot \mathcal{\Theta}\left(1\right)\\ &=\mathcal{\Theta}\left(n^d\right) \end{aligned}
注意 p−1<0p-1<0，故应将分母化为 1−p1-p。
对于 O,Ω\mathcal{O,\Omega}，证明同理。
证毕。

主定理完整版

Θ(nd)\mathcal{\Theta}(n^d) 被换成了更一般的 f(n)f(n)。
T(n)=aT(nb)+f(n)(n≥b)T(n)=aT\left(\frac{n}{b}\right)+f(n)\quad\left(n\ge b\right)
则有：
T(n)={Θ(nlog⁡ba)if  f(n)=O(nlog⁡ba−ϵ)Θ(f(n))if  f(n)=Ω(nlog⁡ba+ϵ)Θ(nlog⁡balog⁡k+1n)if  f(n)=Θ(nlog⁡balog⁡kn)T(n)=\begin{cases} \Theta(n^{\log_b a}) & \text{if}\;f(n)=O(n^{\log_b a-\epsilon})\\ \Theta(f(n)) & \text{if}\;f(n)=\Omega(n^{\log_b a+\epsilon})\\ \Theta(n^{\log_b a}\log^{k+1}n) & \text{if}\;f(n)=\Theta(n^{\log_b a}\log^k n) \end{cases}
其中 ϵ>0,k≥0\epsilon>0,k\ge 0。
注意其中第二条还必须满足正则条件（Regularity Condition），即存在正常数 c<1,n0c<1,n_0 使得 ∀n≥n0\forall n\ge n_0 都有 af(nb)≤cf(n)a f\left(\frac{n}{b}\right) \le c f(n)。
证明比较繁琐，这里不作展开。思路大致就是代入关于 f(n)f(n) 的渐进符号然后化简。
Update 2026.2.1：优化几处格式。

评论

共 10 条评论，欢迎与作者交流。

正在加载评论...