直线和圆的方程 倾斜角:
x x x 轴正向与直线
l l l 向上的方向之间所成的角
α \alpha α 。
斜率:
k = tan α = y 2 − y 1 x 2 − x 1 k=\tan\alpha=\frac{y_2-y_1}{x_2-x_1} k = tan α = x 2 − x 1 y 2 − y 1 。
l 1 ⊥ l 2 ⟹ k 1 ⋅ k 2 = − 1 , ∣ α 1 − α 2 ∣ = 90 ° l_1\perp l_2\implies k_1\cdot k_2=-1,|\alpha_1-\alpha_2|=90\degree l 1 ⊥ l 2 ⟹ k 1 ⋅ k 2 = − 1 , ∣ α 1 − α 2 ∣ = 90° 直线的一般式方程:
A x + B y + C = 0 ⟹ Ax+By+C=0\implies A x + B y + C = 0 ⟹ 斜截式方程
y = − A B x − C B ⟹ y=-\frac{A}{B}x-\frac{C}{B}\implies y = − B A x − B C ⟹ 该直线的方向向量
u → = ( B , − A ) \overrightarrow{u}=(B,-A) u = ( B , − A ) ,法向量
n → = ( A , B ) \overrightarrow{n}=(A,B) n = ( A , B ) 。
点到直线距离公式:
d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 \displaystyle \boxed{d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}} d = A 2 + B 2 ∣ A x 0 + B y 0 + C ∣ 两条平行直线之间距离:
d = ∣ C 1 − C 2 ∣ A 2 + B 2 \displaystyle \boxed{d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}} d = A 2 + B 2 ∣ C 1 − C 2 ∣ 两条平行直线之间的铅锤高差:
h = ∣ C 1 − C 2 ∣ ∣ B ∣ \displaystyle\boxed{h=\frac{|C_1-C_2|}{|B|}} h = ∣ B ∣ ∣ C 1 − C 2 ∣ 若
y = k x + b y=kx+b y = k x + b ,则直线上两点间距离
∣ A B ∣ = 1 + k 2 ∣ x 1 − x 2 ∣ = 1 + 1 k 2 ∣ y 1 − y 2 ∣ |AB|=\sqrt{1+k^2}|x_1-x_2|=\sqrt{1+\frac{1}{k^2}}|y_1-y_2| ∣ A B ∣ = 1 + k 2 ∣ x 1 − x 2 ∣ = 1 + k 2 1 ∣ y 1 − y 2 ∣ 对称问题
点 ( x , y ) (x,y) ( x , y ) ( a , b ) (a,b) ( a , b ) ( 2 a − x , 2 b − y ) (2a-x,2b-y) ( 2 a − x , 2 b − y )
直线 l : A x + B y + C = 0 l:Ax+By+C=0 l : A x + B y + C = 0 ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) A ( 2 x 0 − x ) + B ( 2 y 0 − y ) + C = 0 A(2x_0-x)+B(2y_0-y)+C=0 A ( 2 x 0 − x ) + B ( 2 y 0 − y ) + C = 0
点关于直线的对称点通过设中点来列方程求。
圆 圆的标准方程:
( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 ( x − a ) 2 + ( y − b ) 2 = r 2 圆的一般方程:
x 2 + y 2 + D x + E y + F = 0 x^2+y^2+Dx+Ey+F=0 x 2 + y 2 + D x + E y + F = 0 ,其中
D 2 + E 2 − 4 F > 0 D^2+E^2-4F>0 D 2 + E 2 − 4 F > 0 ,化为标准形式为
( x + D 2 ) 2 + ( y + E 2 ) 2 = D 2 + E 2 − 4 F 4 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\boxed{\left(x+\frac{D}{2}\right)^2+\left(y+\frac{E}{2}\right)^2=\frac{D^2+E^2-4F}{4}} ( x + 2 D ) 2 + ( y + 2 E ) 2 = 4 D 2 + E 2 − 4 F 两圆关系 内含 内切 相交 外切 相离 公切线数 0 0 0 1 1 1 2 2 2 3 3 3 4 4 4
以
( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) ( x 1 , y 1 ) , ( x 2 , y 2 ) 为直径的两端点的圆的方程:
( x − x 1 ) ( x − x 2 ) + ( y − y 1 ) ( y − y 2 ) = 0 (x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0 ( x − x 1 ) ( x − x 2 ) + ( y − y 1 ) ( y − y 2 ) = 0 过圆
( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 ( x − a ) 2 + ( y − b ) 2 = r 2 上一点
( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) 的切线方程为
( x − a ) ( x 0 − a ) + ( y − b ) ( y 0 − b ) = r 2 (x-a)(x_0-a)+(y-b)(y_0-b)=r^2 ( x − a ) ( x 0 − a ) + ( y − b ) ( y 0 − b ) = r 2 过圆
x 2 + y 2 + D x + E y + F = 0 ( D 2 + E 2 − 4 F > 0 ) x^2+y^2+Dx+Ey+F=0\ (D^2+E^2-4F>0) x 2 + y 2 + D x + E y + F = 0 ( D 2 + E 2 − 4 F > 0 ) 上一点
( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) 的切线方程为
x 0 x + y 0 y + D ( x + x 0 ) 2 + E ( y + y 0 ) 2 + F = 0 x_0x+y_0y+\frac{D(x+x_0)}{2}+\frac{E(y+y_0)}{2}+F=0 x 0 x + y 0 y + 2 D ( x + x 0 ) + 2 E ( y + y 0 ) + F = 0 设点
M ( x 0 , y 0 ) M(x_0,y_0) M ( x 0 , y 0 ) 是圆
( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 ( x − a ) 2 + ( y − b ) 2 = r 2 外一点,过点
M M M 作圆的两条切线,切点分别为
A , B A,B A , B ,则直线
A B AB A B 的方程为
( x − a ) ( x 0 − a ) + ( y − b ) ( y 0 − b ) = r 2 (x-a)(x_0-a)+(y-b)(y_0-b)=r^2 ( x − a ) ( x 0 − a ) + ( y − b ) ( y 0 − b ) = r 2 经过圆外一点
P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) 引圆的两条切线,则
圆的方程 切线长公式 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 ( x − a ) 2 + ( y − b ) 2 = r 2 ( x 0 − a ) 2 + ( y 0 − b ) 2 − r 2 \sqrt{(x_0-a)^2+(y_0-b)^2-r^2} ( x 0 − a ) 2 + ( y 0 − b ) 2 − r 2 x 2 + y 2 + D x + E y + F = 0 ( D 2 + E 2 − 4 F > 0 ) x^2+y^2+Dx+Ey+F=0 \\ (D^2+E^2-4F>0) x 2 + y 2 + D x + E y + F = 0 ( D 2 + E 2 − 4 F > 0 ) x 0 2 + y 0 2 + D x 0 + E y 0 + F \sqrt{x_0^2+y_0^2+Dx_0+Ey_0+F} x 0 2 + y 0 2 + D x 0 + E y 0 + F
两圆相交时,两圆方程做差得到公共弦所在直线的方程,即
D 1 x + E 1 y + F 1 − ( D 2 x + E 2 y + F 2 ) = 0 D_1x+E_1y+F_1-(D_2x+E_2y+F_2)=0 D 1 x + E 1 y + F 1 − ( D 2 x + E 2 y + F 2 ) = 0 参数方程:
P ( x , y ) P(x,y) P ( x , y ) 满足
{ x = a + r cos θ y = b + r sin θ ( r > 0 ) \begin{cases}x=a+r\cos\theta \\ y=b+r\sin\theta\end{cases}(r>0) { x = a + r cos θ y = b + r sin θ ( r > 0 ) 的轨迹为
( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 ( x − a ) 2 + ( y − b ) 2 = r 2 。
圆锥曲线的方程 椭圆
概念:平面内到两个焦点 F 1 , F 2 F_1,F_2 F 1 , F 2 ∣ F 1 F 2 ∣ |F_1F_2| ∣ F 1 F 2 ∣
集合
P = { M ∣ ∣ M F 1 ∣ + ∣ M F 2 ∣ = 2 a } , ∣ F 1 F 2 ∣ = 2 c P=\set{M||MF_1|+|MF_2|=2a},|F_1F_2|=2c P = { M ∣ ∣ M F 1 ∣ + ∣ M F 2 ∣ = 2 a } , ∣ F 1 F 2 ∣ = 2 c 标准方程 x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\\ a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) x x x x 2 b 2 + y 2 a 2 = 1 ( a > b > 0 ) \frac{x^2}{b^2}+\frac{y^2}{a^2}=1(a>b>0)\\ b 2 x 2 + a 2 y 2 = 1 ( a > b > 0 ) y y y 顶点坐标 ( ± a , 0 ) , ( 0 , ± b ) (\pm a,0),(0,\pm b) ( ± a , 0 ) , ( 0 , ± b ) ( ± b , 0 ) , ( 0 , ± a ) (\pm b,0),(0,\pm a) ( ± b , 0 ) , ( 0 , ± a ) 对称轴 x x x y y y x x x y y y 焦点坐标 ( ± c , 0 ) (\pm c,0) ( ± c , 0 ) ( 0 , ± c ) (0,\pm c) ( 0 , ± c ) 准线 x = ± a 2 c x=\pm\frac{a^2}{c} x = ± c a 2
c 2 = a 2 − b 2 \boxed{c^2=a^2-b^2} c 2 = a 2 − b 2 e = c a ( 0 < e < 1 ) \boxed{e=\frac{c}{a}}\ (0<e<1) e = a c ( 0 < e < 1 )
椭圆的面积:
S = π a b S=\pi ab S = πab (
a , b a,b a , b 分别为长半轴、短半轴的长 )。
准线:椭圆上一点
M ( x , y ) M(x,y) M ( x , y ) 与顶点
F ( ± c , 0 ) F(\pm c,0) F ( ± c , 0 ) 的距离和它到定直线
l : x = ± a 2 c l:x=\pm\frac{a^2}{c} l : x = ± c a 2 的距离比是常数
e e e ( 椭圆的第二定义 )。
椭圆的第三定义:设
A ( − a , 0 ) , B ( a , 0 ) , P ( x , y ) ∈ C A(-a,0),B(a,0),P(x,y)\in C A ( − a , 0 ) , B ( a , 0 ) , P ( x , y ) ∈ C ,则
k A P ⋅ k B P = − b 2 a 2 = e 2 − 1 \boxed{k_{AP}\cdot k_{BP}=-\frac{b^2}{a^2}=e^2-1} k A P ⋅ k BP = − a 2 b 2 = e 2 − 1 。
椭圆焦点三角形的性质 椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 上异于左、右顶点的点
P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) 与两焦点
F 1 , F 2 F_1,F_2 F 1 , F 2 构成的
Δ P F 1 F 2 \Delta PF_1F_2 Δ P F 1 F 2 叫做焦点三角形。
以下记
∠ F 1 P F 2 = θ \angle F_1PF_2=\theta ∠ F 1 P F 2 = θ 。
周长
C = 2 ( a + c ) C=2(a+c) C = 2 ( a + c ) 。
面积
S = b 2 tan θ 2 = c ∣ y 0 ∣ = 1 2 ∣ P F 1 ∣ ∣ P F 2 ∣ sin θ = r ( a + c ) \boxed{S=b^2\tan\frac{\theta}{2}=c|y_0|=\frac{1}{2}|PF_1||PF_2|\sin\theta=r(a+c)} S = b 2 tan 2 θ = c ∣ y 0 ∣ = 2 1 ∣ P F 1 ∣∣ P F 2 ∣ sin θ = r ( a + c ) ,
r r r 为焦点三角形的内接圆半径,当
y 0 = b y_0=b y 0 = b 即点
P P P 的位置为短轴端点时取最大值,且
cos θ ≥ 1 − 2 e 2 \cos\theta\geq 1-2e^2 cos θ ≥ 1 − 2 e 2 。
证明:由余弦定理,
∣ F 1 F 2 ∣ 2 = ∣ P F 1 ∣ 2 + ∣ P F 2 ∣ 2 − 2 ∣ P F 1 ∣ ∣ P F 2 ∣ cos θ = ( ∣ P F 1 ∣ + ∣ P F 2 ∣ ) 2 − 2 ( 1 + cos θ ) ⋅ ∣ P F 1 ∣ ∣ P F 2 ∣ |F_1F_2|^2=|PF_1|^2+|PF_2|^2-2|PF_1||PF_2|\cos\theta=(|PF_1|+|PF_2|)^2-2(1+\cos\theta)\cdot|PF_1||PF_2| ∣ F 1 F 2 ∣ 2 = ∣ P F 1 ∣ 2 + ∣ P F 2 ∣ 2 − 2∣ P F 1 ∣∣ P F 2 ∣ cos θ = ( ∣ P F 1 ∣ + ∣ P F 2 ∣ ) 2 − 2 ( 1 + cos θ ) ⋅ ∣ P F 1 ∣∣ P F 2 ∣ 因为
∣ P F 1 ∣ + ∣ P F 2 ∣ = 2 a , ∣ F 1 F 2 ∣ = 2 c |PF_1|+|PF_2|=2a,|F_1F_2|=2c ∣ P F 1 ∣ + ∣ P F 2 ∣ = 2 a , ∣ F 1 F 2 ∣ = 2 c ,所以
∣ P F 1 ∣ ∣ P F 2 ∣ = 2 a 2 − 2 c 2 1 + cos θ = 2 b 2 1 + cos θ |PF_1||PF_2|=\frac{2a^2-2c^2}{1+\cos\theta}=\frac{2b^2}{1+\cos\theta} ∣ P F 1 ∣∣ P F 2 ∣ = 1 + c o s θ 2 a 2 − 2 c 2 = 1 + c o s θ 2 b 2 又因为
sin θ 1 + cos θ = 2 sin θ 2 cos θ 2 1 + ( 2 cos 2 θ 2 − 1 ) = sin θ 2 cos θ 2 = tan θ 2 \frac{\sin\theta}{1+\cos\theta}=\frac{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}{1+(2\cos^2\frac{\theta}{2}-1)}=\frac{\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}}=\tan\frac{\theta}{2} 1 + c o s θ s i n θ = 1 + ( 2 c o s 2 2 θ − 1 ) 2 s i n 2 θ c o s 2 θ = c o s 2 θ s i n 2 θ = tan 2 θ 因此
S = 1 2 ∣ P F 1 ∣ ∣ P F 2 ∣ sin θ = b 2 sin θ 1 + cos θ = b 2 tan θ 2 S=\frac{1}{2}|PF_1||PF_2|\sin\theta=\frac{b^2\sin\theta}{1+\cos\theta}=b^2\tan\frac{\theta}{2} S = 2 1 ∣ P F 1 ∣∣ P F 2 ∣ sin θ = 1 + c o s θ b 2 s i n θ = b 2 tan 2 θ
∣ P F 1 ∣ ⋅ ∣ P F 2 ∣ ∈ ( b 2 , a 2 ] |PF_1|\cdot|PF_2|\in (b^2,a^2] ∣ P F 1 ∣ ⋅ ∣ P F 2 ∣ ∈ ( b 2 , a 2 ]
设
∠ P F 1 F 2 = α , P F 2 F 1 = β \angle PF_1F_2=\alpha,PF_2F_1=\beta ∠ P F 1 F 2 = α , P F 2 F 1 = β ,则
e = sin ( α + β ) sin α + sin β = cos α + β 2 cos α − β 2 \displaystyle\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\alpha+\sin\beta}}=\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}} e = sin α + sin β sin ( α + β ) = cos 2 α − β cos 2 α + β ( 证明:正弦定理 )。
若焦点三角形内切圆的圆心为
I I I ,延长
P I PI P I 交
F 1 F 2 F_1F_2 F 1 F 2 于点
Q Q Q ,则
∣ P I ∣ ∣ I Q ∣ = ∣ P F 1 ∣ ∣ F 1 Q ∣ = ∣ P F 2 ∣ ∣ F 2 Q ∣ = ∣ P F 1 ∣ + ∣ P F 2 ∣ ∣ F 1 Q ∣ + ∣ F 2 Q ∣ = 2 a 2 c = 1 e \frac{|PI|}{|IQ|}=\frac{|PF_1|}{|F_1Q|}=\frac{|PF_2|}{|F_2Q|}=\frac{|PF_1|+|PF_2|}{|F_1Q|+|F_2Q|}=\frac{2a}{2c}=\frac{1}{e} ∣ I Q ∣ ∣ P I ∣ = ∣ F 1 Q ∣ ∣ P F 1 ∣ = ∣ F 2 Q ∣ ∣ P F 2 ∣ = ∣ F 1 Q ∣ + ∣ F 2 Q ∣ ∣ P F 1 ∣ + ∣ P F 2 ∣ = 2 c 2 a = e 1
若椭圆上存在点
P P P 使得
∠ F 1 P F 2 = θ \angle F_1PF_2=\theta ∠ F 1 P F 2 = θ ,则
e ∈ [ sin θ 2 , 1 ) e\in[\sin\frac{\theta}{2},1) e ∈ [ sin 2 θ , 1 ) 。
椭圆的其它几何性质
通径:过椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 的焦点作垂直于长轴的直线,该直线被椭圆截得的弦叫做通径,其长度为
2 b 2 a \frac{2b^2}{a} a 2 b 2 。
若不垂直,则其长度为
∣ P P 0 ∣ = 2 b 2 a 1 − e 2 cos 2 θ ≥ 2 b 2 a |PP_0|=\frac{\frac{2b^2}{a}}{1-e^2\cos^2\theta}\geq \frac{2b^2}{a} ∣ P P 0 ∣ = 1 − e 2 c o s 2 θ a 2 b 2 ≥ a 2 b 2
焦半径:设
P ( x , y ) ∈ C , F 1 ( − c , 0 ) , F 2 ( c , 0 ) P(x,y)\in C,F_1(-c,0),F_2(c,0) P ( x , y ) ∈ C , F 1 ( − c , 0 ) , F 2 ( c , 0 ) ,则
∣ P F 1 ∣ = ( x + c ) 2 + b 2 a 2 − x 2 a 2 = c 2 a 2 x 2 + 2 c x + a 2 = ∣ a + e x ∣ |PF_1|=\sqrt{(x+c)^2+b^2\frac{a^2-x^2}{a^2}}=\sqrt{\frac{c^2}{a^2}x^2+2cx+a^2}=|a+ex| ∣ P F 1 ∣ = ( x + c ) 2 + b 2 a 2 a 2 − x 2 = a 2 c 2 x 2 + 2 c x + a 2 = ∣ a + e x ∣ ,同理
∣ P F 2 ∣ = a − e x |PF_2|=a-ex ∣ P F 2 ∣ = a − e x ,因此
∣ P F ∣ = ∣ a ± e x ∣ \boxed{|PF|=|a\pm ex|} ∣ PF ∣ = ∣ a ± e x ∣ 。
焦点弦( 过焦点的弦 ):设
A B AB A B 是过椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ (a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 的右焦点
F F F 的一条弦,
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , A B A(x_1,y_1),B(x_2,y_2),AB A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , A B 的倾斜角为
θ \theta θ ,准线
l : x = a 2 c l:x=\frac{a^2}{c} l : x = c a 2 ,则
∣ A F ∣ ∣ B F ∣ = 1 − e cos θ 1 + e cos θ , ∣ A B ∣ = 2 a ( 1 − e 2 ) 1 − e 2 cos 2 θ \boxed{\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta},|AB|=\frac{2a(1-e^2)}{1-e^2\cos^2\theta}} ∣ BF ∣ ∣ A F ∣ = 1 + e cos θ 1 − e cos θ , ∣ A B ∣ = 1 − e 2 cos 2 θ 2 a ( 1 − e 2 ) 。
证明:过
A A A 作
A A 1 ⊥ A B AA_1\perp AB A A 1 ⊥ A B 于点
A 1 A_1 A 1 ,则
∣ A F ∣ = e ∣ A A 1 ∣ = e ( a 2 c − c − ∣ A F ∣ cos θ ) ⟹ ∣ A F ∣ = b 2 a + c cos θ |AF|=e|AA_1|=e(\frac{a^2}{c}-c-|AF|\cos\theta)\implies|AF|=\frac{b^2}{a+c\cos\theta} ∣ A F ∣ = e ∣ A A 1 ∣ = e ( c a 2 − c − ∣ A F ∣ cos θ ) ⟹ ∣ A F ∣ = a + c c o s θ b 2 同理
∣ B F ∣ = b 2 a − c cos θ |BF|=\frac{b^2}{a-c\cos\theta} ∣ BF ∣ = a − c c o s θ b 2 ,代入得证。
注:一条过焦点的直线会有两个一长一短的焦半径,在公式中,
长的对应取减号,短的对应取加号;当焦点在 y y y cos θ \cos\theta cos θ sin θ \sin\theta sin θ 。
过一个焦点
F F F 作弦
A B , A F = d 1 , B F = d 2 AB,AF=d_1,BF=d_2 A B , A F = d 1 , BF = d 2 ,则
1 d 1 + 1 d 2 = 2 a b 2 \displaystyle\frac{1}{d_1}+\frac{1}{d_2}=\frac{2a}{b^2} d 1 1 + d 2 1 = b 2 2 a
弦长公式:设直线
y = k x + m y=kx+m y = k x + m 与椭圆有两个公共点
M ( x 1 , y 1 ) , N ( x 2 y 2 ) M(x_1,y_1),N(x_2y_2) M ( x 1 , y 1 ) , N ( x 2 y 2 ) ,则弦长公式:
∣ M N ∣ = ( 1 + k 2 ) [ ( x 1 + x 2 ) 2 − 4 x 1 x 2 ] = ( 1 + 1 k 2 ) [ ( y 1 + y 2 ) 2 − 4 y 1 y 2 ] |MN|=\sqrt{(1+k^2)[(x_1+x_2)^2-4x_1x_2]}=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]} ∣ MN ∣ = ( 1 + k 2 ) [( x 1 + x 2 ) 2 − 4 x 1 x 2 ] = ( 1 + k 2 1 ) [( y 1 + y 2 ) 2 − 4 y 1 y 2 ]
中点弦问题:求直线
A B AB A B 与圆锥曲线相交弦的中点
M M M 和原点的连线
O M OM OM 的斜率问题,
\\ 有
k A B ⋅ k O M = − b 2 a 2 = e 2 − 1 \boxed{k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}=e^2-1} k A B ⋅ k OM = − a 2 b 2 = e 2 − 1 ( 若焦点在
y y y 轴,则
k A B ⋅ k O M = − a 2 b 2 k_{AB}\cdot k_{OM}=-\frac{a^2}{b^2} k A B ⋅ k OM = − b 2 a 2 )
证明:联立
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ (a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 与
y = k A B x + m y=k_{AB}x+m y = k A B x + m 得
( b 2 + a 2 k A B 2 ) x 2 + 2 m k A B a 2 x + a 2 m 2 − a 2 b 2 = 0 (b^2+a^2k_{AB}^2)x^2+2mk_{AB}a^2x+a^2m^2-a^2b^2=0 ( b 2 + a 2 k A B 2 ) x 2 + 2 m k A B a 2 x + a 2 m 2 − a 2 b 2 = 0 所以
x 1 + x 2 = − 2 m k A B a 2 b 2 + a 2 k A B 2 , M x = x 1 + x 2 2 = − m k A B a 2 b 2 + a 2 k A B 2 , m = b 2 + a 2 k A B 2 − k A B a 2 M x x_1+x_2=\frac{-2mk_{AB}a^2}{b^2+a^2k_{AB}^2},M_x=\frac{x_1+x_2}{2}=\frac{-mk_{AB}a^2}{b^2+a^2k_{AB}^2},m=\frac{b^2+a^2k_{AB}^2}{-k_{AB}a^2}M_x x 1 + x 2 = b 2 + a 2 k A B 2 − 2 m k A B a 2 , M x = 2 x 1 + x 2 = b 2 + a 2 k A B 2 − m k A B a 2 , m = − k A B a 2 b 2 + a 2 k A B 2 M x 代入
y = k A B x + m y=k_{AB}x+m y = k A B x + m 得
y = − b 2 k A B a 2 x ⟹ k A B ⋅ k O M = − b 2 a 2 y=-\frac{b^2}{k_{AB}a^2}x\implies k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2} y = − k A B a 2 b 2 x ⟹ k A B ⋅ k OM = − a 2 b 2 例题:过椭圆
x 2 16 + y 2 4 = 1 \frac{x^2}{16}+\frac{y^2}{4}=1 16 x 2 + 4 y 2 = 1 内一点
P ( 3 , 1 ) P(3,1) P ( 3 , 1 ) ,且被这点平分的弦所在的直线方程是 ?
方法一:设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ⟹ x 1 2 16 + y 1 2 4 = 1 , x 2 2 16 + y 2 2 4 = 1 A(x_1,y_1),B(x_2,y_2)\implies \frac{x_1^2}{16}+\frac{y_1^2}{4}=1,\frac{x_2^2}{16}+\frac{y_2^2}{4}=1 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ⟹ 16 x 1 2 + 4 y 1 2 = 1 , 16 x 2 2 + 4 y 2 2 = 1 ,两式相减得
( x 1 + x 2 ) ( x 1 − x 2 ) 16 + ( y 1 + y 2 ) ( y 1 − y 2 ) 4 = 0 \frac{(x_1+x_2)(x_1-x_2)}{16}+\frac{(y_1+y_2)(y_1-y_2)}{4}=0 16 ( x 1 + x 2 ) ( x 1 − x 2 ) + 4 ( y 1 + y 2 ) ( y 1 − y 2 ) = 0 P P P 为
A B AB A B 中点
⟹ x 1 + x 2 = 6 , y 1 + y 2 = 2 ⟹ k A B = y 1 − y 2 x 1 − x 2 = − 3 4 \implies x_1+x_2=6,y_1+y_2=2 \implies k_{AB}=\frac{y_1-y_2}{x_1-x_2}=-\frac{3}{4} ⟹ x 1 + x 2 = 6 , y 1 + y 2 = 2 ⟹ k A B = x 1 − x 2 y 1 − y 2 = − 4 3 所以直线
A B AB A B 的方程是
3 x + 4 y − 13 = 0 3x+4y-13=0 3 x + 4 y − 13 = 0 。
方法二:设弦为
A B , k O P = 1 3 , k A B = − b 2 a 2 ÷ 1 3 = − 3 4 AB,k_{OP}=\frac{1}{3},k_{AB}=-\frac{b^2}{a^2}\div\frac{1}{3}=-\frac{3}{4} A B , k OP = 3 1 , k A B = − a 2 b 2 ÷ 3 1 = − 4 3 ,后同方法一。
中点弦问题的推广:椭圆上的点
P P P 与过椭圆中心的弦
A B AB A B 的端点的连线
M A , M B MA,MB M A , MB 斜率之积为
− b 2 a 2 = e 2 − 1 \boxed{-\frac{b^2}{a^2}=e^2-1} − a 2 b 2 = e 2 − 1 证明:作中位线
O T OT OT ,易证
k M A ⋅ k M B = k M A ⋅ k O T = − b 2 a 2 = e 2 − 1 k_{MA}\cdot k_{MB}=k_{MA}\cdot k_{OT}=-\frac{b^2}{a^2}=e^2-1 k M A ⋅ k MB = k M A ⋅ k OT = − a 2 b 2 = e 2 − 1
蒙日圆:椭圆上两条互相垂直的切线的交点必在一个
与椭圆同心的圆 上,且圆的方程为
x 2 + y 2 = a 2 + b 2 x^2+y^2=a^2+b^2 x 2 + y 2 = a 2 + b 2 。
过蒙日圆上一点
M M M 做关于椭圆的切线,与椭圆交于
A , B A,B A , B ,
D D D 为椭圆上任意一点,则
k D A k D B = e 2 − 1 \boxed{k_{DA}k_{DB}=e^2-1} k D A k D B = e 2 − 1 。
椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 在
( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) 处的切线方程为
x 0 x a 2 + y 0 y b 2 = 1 \frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1 a 2 x 0 x + b 2 y 0 y = 1 ,直接设直线
y = k x + m y=kx+m y = k x + m ,算
Δ \Delta Δ 得证。
过椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 上任意一点
P P P ( 不是椭圆的顶点 )作椭圆的切线,设切线的斜率为
k 1 k_1 k 1 ,直线
O P OP OP 的斜率为
k 2 k_2 k 2 ,则
k 1 k 2 = e 2 − 1 \boxed{k_1k_2=e^2-1} k 1 k 2 = e 2 − 1 ,
双曲线同样成立 。
过原点
O O O 的直线
l l l 与椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 相交于
A , B A,B A , B 两点,
P P P 为椭圆上任意一点,则
k P A k P B = e 2 − 1 k_{PA}k_{PB}=e^2-1 k P A k PB = e 2 − 1 。
过椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 上的任意一点
P P P ( 非顶点 )作倾斜角互补的两条直线交椭圆于
A , B A,B A , B 两点,有
k A B k O P = 1 − e 2 k_{AB}k_{OP}=1-e^2 k A B k OP = 1 − e 2 。
如果是焦点在 y y y e 2 − 1 → 1 e 2 − 1 \boxed{e^2-1\to\frac{1}{e^2-1}} e 2 − 1 → e 2 − 1 1 。
A , B A,B A , B 是椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 上任意两点,
S Δ A O B max = 1 2 a b S_{\Delta AOB\max}=\frac{1}{2}ab S Δ A OB m a x = 2 1 ab 。
A , B A,B A , B 是椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 上任意两点,并且
O A ⊥ O B ⟹ 1 ∣ O A ∣ 2 + 1 ∣ O B ∣ 2 = 1 a 2 + 1 b 2 OA\perp OB\implies \frac{1}{|OA|^2}+\frac{1}{|OB|^2}=\frac{1}{a^2}+\frac{1}{b^2} O A ⊥ OB ⟹ ∣ O A ∣ 2 1 + ∣ OB ∣ 2 1 = a 2 1 + b 2 1 。
椭圆两焦点到椭圆上任意一条切线的距离之积为定值
b 2 b^2 b 2 。
证明:设切点为
( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) ,切线方程为
b 2 x 0 x + a 2 y 0 y = a 2 b 2 b^2x_0x+a^2y_0y=a^2b^2 b 2 x 0 x + a 2 y 0 y = a 2 b 2 ,距离
d 1 = ∣ − b 2 x 0 c − a 2 b 2 ∣ b 4 x 0 2 + a 4 y 0 2 , d 2 = ∣ b 2 x 0 c − a 2 b 2 ∣ b 4 x 0 2 + a 4 y 0 2 d_1=\frac{|-b^2x_0c-a^2b^2|}{\sqrt{b^4x_0^2+a^4y_0^2}},d_2=\frac{|b^2x_0c-a^2b^2|}{\sqrt{b^4x_0^2+a^4y_0^2}} d 1 = b 4 x 0 2 + a 4 y 0 2 ∣ − b 2 x 0 c − a 2 b 2 ∣ , d 2 = b 4 x 0 2 + a 4 y 0 2 ∣ b 2 x 0 c − a 2 b 2 ∣ ,则
d 1 d 2 = ∣ a 4 b 4 − b 4 x 0 2 c 2 ∣ b 4 x 0 2 + a 4 y 0 2 = b 2 x 0 2 + a 2 y 0 2 = a 2 b 2 b 2 a 4 b 2 − a 2 b 2 x 0 2 + b 4 x 0 2 b 4 x 0 2 + a 4 b 2 − a 2 b 2 x 0 2 = b 2 d_1d_2=\frac{|a^4b^4-b^4x_0^2c^2|}{b^4x_0^2+a^4y_0^2}\xlongequal{b^2x_0^2+a^2y_0^2=a^2b^2}b^2\frac{a^4b^2-a^2b^2x_0^2+b^4x_0^2}{b^4x_0^2+a^4b^2-a^2b^2x_0^2}=b^2 d 1 d 2 = b 4 x 0 2 + a 4 y 0 2 ∣ a 4 b 4 − b 4 x 0 2 c 2 ∣ b 2 x 0 2 + a 2 y 0 2 = a 2 b 2 b 2 b 4 x 0 2 + a 4 b 2 − a 2 b 2 x 0 2 a 4 b 2 − a 2 b 2 x 0 2 + b 4 x 0 2 = b 2
好题
设直线 l : y = x + 1 l:y=x+1 l : y = x + 1 C : x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) C : a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) A , B A,B A , B x x x F F F A F → = 3 F B → \overrightarrow{AF}=3\overrightarrow{FB} A F = 3 FB e = e= e =
答案:
2 2 \frac{\sqrt{2}}{2} 2 2 解析:方法一:由题得
F ( − 1 , 0 ) , c = 1 F(-1,0),c=1 F ( − 1 , 0 ) , c = 1 ,设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ,联立
y = x + 1 y=x+1 y = x + 1 与椭圆方程
b 2 x 2 + a 2 y 2 = a 2 b 2 b^2x^2+a^2y^2=a^2b^2 b 2 x 2 + a 2 y 2 = a 2 b 2 得
( a 2 + b 2 ) y 2 − 2 b 2 y + b 2 − a 2 b 2 = 0 (a^2+b^2)y^2-2b^2y+b^2-a^2b^2=0 ( a 2 + b 2 ) y 2 − 2 b 2 y + b 2 − a 2 b 2 = 0 ,显然
Δ > 0 , y 1 + y 2 = 2 b 2 a 2 + b 2 , y 1 y 2 = b 2 − a 2 b 2 a 2 + b 2 ⊛ \Delta>0,y_1+y_2=\frac{2b^2}{a^2+b^2},y_1y_2=\frac{b^2-a^2b^2}{a^2+b^2}\ \circledast Δ > 0 , y 1 + y 2 = a 2 + b 2 2 b 2 , y 1 y 2 = a 2 + b 2 b 2 − a 2 b 2 ⊛ 由
A F → = 3 F B → \overrightarrow{AF}=3\overrightarrow{FB} A F = 3 FB 得
0 − y 1 = 3 ( y 2 − 0 ) 0-y_1=3(y_2-0) 0 − y 1 = 3 ( y 2 − 0 ) 即
y 1 = − 3 y 2 ⊚ y_1=-3y_2\ \circledcirc y 1 = − 3 y 2 ⊚ 由
⊛ ⊚ \circledast \circledcirc ⊛⊚ 消去
y 1 , y 2 y_1,y_2 y 1 , y 2 得
− 3 b 2 = ( a 2 + b 2 ) ( 1 − a 2 ) ⇒ a 2 − b 2 = c 2 = 1 a 4 − 3 a 2 + 1 = 0 ⟹ a = ± 2 or ± 1 -3b^2=(a^2+b^2)(1-a^2)\xRightarrow{a^2-b^2=c^2=1}a^4-3a^2+1=0\implies a=\pm\sqrt{2}\ \text{or}\ \pm 1 − 3 b 2 = ( a 2 + b 2 ) ( 1 − a 2 ) a 2 − b 2 = c 2 = 1 a 4 − 3 a 2 + 1 = 0 ⟹ a = ± 2 or ± 1 取
a = 2 a=\sqrt{2} a = 2 ,所以
e = c a = 2 2 e=\frac{c}{a}=\frac{\sqrt{2}}{2} e = a c = 2 2 。
方法二:注意上述关于焦点弦的结论,
∣ A F ∣ ∣ B F ∣ = 1 − e cos θ 1 + e cos θ = 3 \frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta}=3 ∣ BF ∣ ∣ A F ∣ = 1 + e c o s θ 1 − e c o s θ = 3 ,代入
cos θ = 2 2 \cos\theta=\frac{\sqrt{2}}{2} cos θ = 2 2 可得
e = 2 2 e=\frac{\sqrt{2}}{2} e = 2 2
已知椭圆 x 2 4 + y 2 = 1 \frac{x^2}{4}+y^2=1 4 x 2 + y 2 = 1 l : y = k x + m l:y=kx+m l : y = k x + m m ≠ − 2 k m\neq -2k m = − 2 k A , B A,B A , B A B AB A B Q ( 2 , 0 ) Q(2,0) Q ( 2 , 0 ) l l l
解:设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ,联立
{ y = k x + m x 2 4 + y 2 = 1 \begin{cases}
y=kx+m \\
\frac{x^2}{4}+y^2=1
\end{cases} { y = k x + m 4 x 2 + y 2 = 1 得
( 1 + 4 k 2 ) x 2 + 8 k m x + 4 m 2 − 4 = 0 , Δ = 16 ( 4 k 2 − m + 1 ) > 0 (1+4k^2)x^2+8kmx+4m^2-4=0,\Delta=16(4k^2-m+1)>0 ( 1 + 4 k 2 ) x 2 + 8 km x + 4 m 2 − 4 = 0 , Δ = 16 ( 4 k 2 − m + 1 ) > 0 则
x 1 + x 2 = − 8 k m 1 + 4 k 2 , x 1 x 2 = 4 m 2 − 4 1 + 4 k 2 , y 1 y 2 = ( k x 1 + m ) ( k x 2 + m ) = k 2 x 1 x 2 + k m ( x 1 + x 2 ) + m 2 = m 2 − 4 k 2 1 + 4 k 2 x_1+x_2=\frac{-8km}{1+4k^2},x_1x_2=\frac{4m^2-4}{1+4k^2},y_1y_2=(kx_1+m)(kx_2+m)=k^2x_1x_2+km(x_1+x_2)+m^2=\frac{m^2-4k^2}{1+4k^2} x 1 + x 2 = 1 + 4 k 2 − 8 km , x 1 x 2 = 1 + 4 k 2 4 m 2 − 4 , y 1 y 2 = ( k x 1 + m ) ( k x 2 + m ) = k 2 x 1 x 2 + km ( x 1 + x 2 ) + m 2 = 1 + 4 k 2 m 2 − 4 k 2 因为以线段
A B AB A B 为直径的圆过点
Q Q Q ,所以
Q B → ⋅ Q A → = 0 \overrightarrow{QB}\cdot\overrightarrow{QA}=0 QB ⋅ Q A = 0 ,又
Q B → = ( x 2 − 2 , y 2 ) , Q A → = ( x 1 − 2 , y 1 ) \overrightarrow{QB}=(x_2-2,y_2),\overrightarrow{QA}=(x_1-2,y_1) QB = ( x 2 − 2 , y 2 ) , Q A = ( x 1 − 2 , y 1 ) 所以
Q B → ⋅ Q A → = x 1 x 2 − 2 ( x 1 + x 2 ) + 4 + y 1 y 2 = ( 6 k + 5 m ) ( 2 k + m ) 1 + 4 k 2 = 0 \overrightarrow{QB}\cdot\overrightarrow{QA}=x_1x_2-2(x_1+x_2)+4+y_1y_2=\frac{(6k+5m)(2k+m)}{1+4k^2}=0 QB ⋅ Q A = x 1 x 2 − 2 ( x 1 + x 2 ) + 4 + y 1 y 2 = 1 + 4 k 2 ( 6 k + 5 m ) ( 2 k + m ) = 0 显然
m = − 6 5 k ⟹ l : y = k x − 6 5 k = k ( x − 6 5 ) m=-\frac{6}{5}k\implies l:y=kx-\frac{6}{5}k=k(x-\frac{6}{5}) m = − 5 6 k ⟹ l : y = k x − 5 6 k = k ( x − 5 6 ) ,恒过定点
( 6 5 , 0 ) (\frac{6}{5},0) ( 5 6 , 0 ) 。
(
齐次化 )3. 已知
x 2 4 + y 2 3 = 1 \frac{x^2}{4}+\frac{y^2}{3}=1 4 x 2 + 3 y 2 = 1 ,是否存在定圆与
M N ( O M ⊥ O N ) MN(OM\perp ON) MN ( OM ⊥ ON ) ( 动直线 )总相切 ?
设
M N : m x + n y = 1 MN:mx+ny=1 MN : m x + n y = 1 ,代入得
3 x 2 + 4 y 2 − 12 ( m x + n y ) 2 = 0 ⟹ ( 3 − 12 m 2 ) x 2 + ( 4 − 12 n 2 ) y 2 − 24 m n x y = 0 3x^2+4y^2-12(mx+ny)^2=0\implies (3-12m^2)x^2+(4-12n^2)y^2-24mnxy=0 3 x 2 + 4 y 2 − 12 ( m x + n y ) 2 = 0 ⟹ ( 3 − 12 m 2 ) x 2 + ( 4 − 12 n 2 ) y 2 − 24 mn x y = 0 化成
( 4 − 12 n 2 ) k 2 − 24 m n k + 3 − 12 m 2 = 0 (4-12n^2)k^2-24mnk+3-12m^2=0 ( 4 − 12 n 2 ) k 2 − 24 mnk + 3 − 12 m 2 = 0 ,因为
k 1 k 2 = 3 − 12 m 2 4 − 12 n 2 = − 1 k_1k_2=\frac{3-12m^2}{4-12n^2}=-1 k 1 k 2 = 4 − 12 n 2 3 − 12 m 2 = − 1 ,因此
m 2 + n 2 = 7 12 m^2+n^2=\frac{7}{12} m 2 + n 2 = 12 7 ,定圆为
x 2 + y 2 = 12 7 x^2+y^2=\frac{12}{7} x 2 + y 2 = 7 12 。
(
定比点差法 )4. 已知
x 2 4 + y 2 = 1 , A ( − 2 , 0 ) \frac{x^2}{4}+y^2=1,A(-2,0) 4 x 2 + y 2 = 1 , A ( − 2 , 0 ) ,经过
B ( 1 , 0 ) B(1,0) B ( 1 , 0 ) 且斜率存在的直线
l l l 交椭圆于
P , Q P,Q P , Q 两点,点
C C C 与点
P P P 关于坐标原点对称,连接
A C , A Q AC,AQ A C , A Q ,求
k A C k A Q \frac{k_{AC}}{k_{AQ}} k A Q k A C 的值。
设
P ( x 1 , y 1 ) , Q ( x 2 , y 2 ) , P B → = λ B Q → P(x_1,y_1),Q(x_2,y_2),\overrightarrow{PB}=\lambda\overrightarrow{BQ} P ( x 1 , y 1 ) , Q ( x 2 , y 2 ) , PB = λ BQ ,则
x 1 + λ x 2 = 1 + λ , y 1 + λ y 2 = 0 x_1+\lambda x_2=1+\lambda,y_1+\lambda y_2=0 x 1 + λ x 2 = 1 + λ , y 1 + λ y 2 = 0 { x 1 2 4 + y 1 2 = 1 x 2 2 4 + y 2 2 = 1 ⟹ { x 1 2 4 + y 1 2 = 1 λ x 2 2 4 + λ y 2 2 = λ \begin{cases} \frac{x_1^2}{4}+y_1^2=1 \\ \frac{x_2^2}{4}+y_2^2=1 \end{cases}\implies \begin{cases} \frac{x_1^2}{4}+y_1^2=1 \\ \frac{\lambda x_2^2}{4}+\lambda y_2^2=\lambda \end{cases} { 4 x 1 2 + y 1 2 = 1 4 x 2 2 + y 2 2 = 1 ⟹ { 4 x 1 2 + y 1 2 = 1 4 λ x 2 2 + λ y 2 2 = λ 两式作差得
( x 1 + λ x 2 ) ( x 1 − λ x 2 ) 4 + ( y 1 + λ y 2 ) ( y 1 − λ y 2 ) = 1 − λ 2 \frac{(x_1+\lambda x_2)(x_1-\lambda x_2)}{4}+(y_1+\lambda y_2)(y_1-\lambda y_2)=1-\lambda ^2 4 ( x 1 + λ x 2 ) ( x 1 − λ x 2 ) + ( y 1 + λ y 2 ) ( y 1 − λ y 2 ) = 1 − λ 2 代入解得
x 1 = 5 − 3 λ 2 , x 2 = 5 λ − 3 2 λ , k A C k A Q = y 1 ( x 2 + 2 ) y 2 ( x 1 − 2 ) = − λ ( x 2 + 2 ) x 1 − 2 = 3 − 9 λ 1 − 3 λ = 3 x_1=\frac{5-3\lambda}{2},x_2=\frac{5\lambda -3}{2\lambda},\frac{k_{AC}}{k_{AQ}}=\frac{y_1(x_2+2)}{y_2(x_1-2)}=\frac{-\lambda(x_2+2)}{x_1-2}=\frac{3-9\lambda}{1-3\lambda}=3 x 1 = 2 5 − 3 λ , x 2 = 2 λ 5 λ − 3 , k A Q k A C = y 2 ( x 1 − 2 ) y 1 ( x 2 + 2 ) = x 1 − 2 − λ ( x 2 + 2 ) = 1 − 3 λ 3 − 9 λ = 3
练习题:设 F 1 , F 2 F_1,F_2 F 1 , F 2 x 2 3 + y 2 = 1 \frac{x^2}{3}+y^2=1 3 x 2 + y 2 = 1 A , B A,B A , B F 1 A → = 5 F 2 B → \overrightarrow{F_1A}=5\overrightarrow{F_2B} F 1 A = 5 F 2 B A A A ( 0 , ± 1 ) (0,\pm 1) ( 0 , ± 1 )
(
正难则反 )5. 设椭圆
x 2 a 2 + y 2 = 1 ( a > 1 ) \frac{x^2}{a^2}+y^2=1(a>1) a 2 x 2 + y 2 = 1 ( a > 1 ) ,若以点
A ( 0 , 1 ) A(0,1) A ( 0 , 1 ) 为圆心的圆与椭圆至多有
3 3 3 个公共点,求
e e e 范围?
从反面考虑,若有
4 4 4 个公共点,可知在
y y y 轴两侧各有
2 2 2 个交点,可知椭圆的一侧存在一个等腰
Δ A P Q , A P = A Q \Delta APQ,AP=AQ Δ A PQ , A P = A Q 。
设
P Q PQ PQ 中点为
M ( x 0 , y 0 ) M(x_0,y_0) M ( x 0 , y 0 ) ,则
k O M k P Q = e 2 − 1 = − 1 a 2 k_{OM}k_{PQ}=e^2-1=-\frac{1}{a^2} k OM k PQ = e 2 − 1 = − a 2 1 。因为
k A M k P Q = y 0 − 1 x 0 k P Q = − 1 k_{AM}k_{PQ}=\frac{y_0-1}{x_0}k_{PQ}=-1 k A M k PQ = x 0 y 0 − 1 k PQ = − 1 ,
两式相除得
y 0 − 1 y 0 = a 2 > 2 \frac{y_0-1}{y_0}=a^2>2 y 0 y 0 − 1 = a 2 > 2 ,得出
e ∈ ( 0 , 2 2 ] e\in(0,\frac{\sqrt{2}}{2}] e ∈ ( 0 , 2 2 ] 。
(
齐次化 )6. ( 2022 I 卷,T22 )已知
C : x 2 6 + y 2 3 = 1 , A ( 2 , 1 ) C:\frac{x^2}{6}+\frac{y^2}{3}=1,A(2,1) C : 6 x 2 + 3 y 2 = 1 , A ( 2 , 1 ) ,点
M , N M,N M , N 在
C C C 上,
A M ⊥ A N , A D ⊥ M N AM\perp AN,AD\perp MN A M ⊥ A N , A D ⊥ MN ,
D D D 为垂足,证明:存在定点
Q Q Q ,使得
∣ D Q ∣ |DQ| ∣ D Q ∣ 是定值。
方法一:设
M N : y = k x + m MN:y=kx+m MN : y = k x + m ,暴力联立
+ + + 向量得
( 2 k + 3 m + 1 ) ( 2 k + m − 1 ) = 0 (2k+3m+1)(2k+m-1)=0 ( 2 k + 3 m + 1 ) ( 2 k + m − 1 ) = 0 ,得出
M N MN MN 过定点
P ( 2 3 , − 1 3 ) P(\frac{2}{3},-\frac{1}{3}) P ( 3 2 , − 3 1 ) 。令
Q ( 4 3 , 1 3 ) Q(\frac{4}{3},\frac{1}{3}) Q ( 3 4 , 3 1 ) 为
A P AP A P 中点,得出
∣ D Q ∣ = 1 2 ∣ A P ∣ = 2 2 3 |DQ|=\frac{1}{2}|AP|=\frac{2\sqrt{2}}{3} ∣ D Q ∣ = 2 1 ∣ A P ∣ = 3 2 2 是定值。
方法二:先将
C C C 平移一下,变为
( x + 2 ) 2 6 + ( y + 1 ) 2 3 = 1 \frac{(x+2)^2}{6}+\frac{(y+1)^2}{3}=1 6 ( x + 2 ) 2 + 3 ( y + 1 ) 2 = 1 ,使得
A A A 点在新坐标的原点上。设
M N : m x + n y = 1 MN:mx+ny=1 MN : m x + n y = 1 ,联立得
( 2 + 4 n ) ( y x ) 2 + 4 ( m + n ) y x + 4 m + 1 = 0 (2+4n)(\frac{y}{x})^2+4(m+n)\frac{y}{x}+4m+1=0 ( 2 + 4 n ) ( x y ) 2 + 4 ( m + n ) x y + 4 m + 1 = 0 ,显然
y 1 y 2 x 1 x 2 = 4 m + 1 2 + 4 n = − 1 \frac{y_1y_2}{x_1x_2}=\frac{4m+1}{2+4n}=-1 x 1 x 2 y 1 y 2 = 2 + 4 n 4 m + 1 = − 1 ,得到
( − 4 3 ) m + ( − 4 3 ) n = 1 (-\frac{4}{3})m+(-\frac{4}{3})n=1 ( − 3 4 ) m + ( − 3 4 ) n = 1 ,即定点
( 2 3 , − 1 3 ) (\frac{2}{3},-\frac{1}{3}) ( 3 2 , − 3 1 ) 。
(
点差法 + 二次代换消元 )7. ( 华附 2024 5 月测试 )已知
E : x 2 4 + y 2 = 1 E:\frac{x^2}{4}+y^2=1 E : 4 x 2 + y 2 = 1 ,
E E E 上有
3 3 3 点
G , S , T G,S,T G , S , T ,直线
S T ST ST 过点
C ( 2 , 2 ) C(2,2) C ( 2 , 2 ) ,点
M M M 为
G S GS GS 中点且在直线
y = x y=x y = x 上,证明:直线
G T GT GT 与直线
y = x y=x y = x 的交点为定点。
设
S ( x 1 , y 1 ) , T ( x 2 , y 2 ) , G ( x 3 , y 3 ) S(x_1,y_1),T(x_2,y_2),G(x_3,y_3) S ( x 1 , y 1 ) , T ( x 2 , y 2 ) , G ( x 3 , y 3 ) ,进行一次点差法:
x 1 2 4 + y 1 2 = 1 , x 3 2 4 + y 3 2 = 1 \frac{x_1^2}{4}+y_1^2=1,\frac{x_3^2}{4}+y_3^2=1 4 x 1 2 + y 1 2 = 1 , 4 x 3 2 + y 3 2 = 1 ,相减得
y 1 − y 3 x 1 − x 3 = − y 1 + y 3 4 ( x 1 + x 3 ) \frac{y_1-y_3}{x_1-x_3}=-\frac{y_1+y_3}{4(x_1+x_3)} x 1 − x 3 y 1 − y 3 = − 4 ( x 1 + x 3 ) y 1 + y 3 因为
G T GT GT 中点在
y = x y=x y = x 上所以
y 1 + y 3 = x 1 + x 3 y_1+y_3=x_1+x_3 y 1 + y 3 = x 1 + x 3 得
y 1 − y 3 = − 1 4 ( x 1 − x 3 ) y_1-y_3=-\frac{1}{4}(x_1-x_3) y 1 − y 3 = − 4 1 ( x 1 − x 3 ) 。
两式相加得
2 y 1 = 3 4 x 1 + 5 4 x 3 ⟹ x 3 = 8 y 1 − 3 x 1 5 , y 3 = 3 y 1 + 2 x 1 5 2y_1=\frac{3}{4}x_1+\frac{5}{4}x_3\implies x_3=\frac{8y_1-3x_1}{5},y_3=\frac{3y_1+2x_1}{5} 2 y 1 = 4 3 x 1 + 4 5 x 3 ⟹ x 3 = 5 8 y 1 − 3 x 1 , y 3 = 5 3 y 1 + 2 x 1 代入
G T : y − y 3 x − x 3 = y − y 2 x − x 2 GT:\frac{y-y_3}{x-x_3}=\frac{y-y_2}{x-x_2} GT : x − x 3 y − y 3 = x − x 2 y − y 2 得
( 5 y 2 − 3 y 1 − 2 x 1 ) x + ( 8 y 1 − 3 x 1 − 5 x 2 ) y = − 3 ( x 1 y 2 + x 2 y 1 ) + 8 y 1 y 2 − 2 x 1 x 2 (5y_2-3y_1-2x_1)x+(8y_1-3x_1-5x_2)y=-3(x_1y_2+x_2y_1)+8y_1y_2-2x_1x_2 ( 5 y 2 − 3 y 1 − 2 x 1 ) x + ( 8 y 1 − 3 x 1 − 5 x 2 ) y = − 3 ( x 1 y 2 + x 2 y 1 ) + 8 y 1 y 2 − 2 x 1 x 2 设交点为
( m , m ) (m,m) ( m , m ) ,代入得
5 m ( y 1 + y 2 ) − 5 m ( x 1 + x 2 ) = 8 y 1 y 2 − 2 x 1 x 2 − 3 ( x 1 y 2 + x 2 y 1 ) 5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1) 5 m ( y 1 + y 2 ) − 5 m ( x 1 + x 2 ) = 8 y 1 y 2 − 2 x 1 x 2 − 3 ( x 1 y 2 + x 2 y 1 ) 由直线
S T ST ST 过点
C ( 2 , 2 ) , y 2 − 2 x 2 − 2 = y 1 − 2 x 1 − 2 ⟹ x 1 ( y 2 − 2 ) − x 2 ( y 1 − 2 ) = 2 ( y 2 − y 1 ) C(2,2),\frac{y_2-2}{x_2-2}=\frac{y_1-2}{x_1-2}\implies x_1(y_2-2)-x_2(y_1-2)=2(y_2-y_1) C ( 2 , 2 ) , x 2 − 2 y 2 − 2 = x 1 − 2 y 1 − 2 ⟹ x 1 ( y 2 − 2 ) − x 2 ( y 1 − 2 ) = 2 ( y 2 − y 1 ) ,进行二次代换凑出和积:
x 1 ( y 2 − 2 ) + x 2 ( y 1 − 2 ) = x 1 2 ( y 2 − 2 ) 2 − x 2 2 ( y 1 − 2 ) 2 x 1 ( y 2 − 2 ) − x 2 ( y 1 − 2 ) = ( 4 − 4 y 1 2 ) ( y 2 − 2 ) 2 − ( 4 − 4 y 2 2 ) ( y 1 − 2 ) 2 2 ( y 2 − y 1 ) = 10 ( y 1 + y 2 ) − 8 − 8 y 1 y 2 x_1(y_2-2)+x_2(y_1-2)=\frac{x_1^2(y_2-2)^2-x_2^2(y_1-2)^2}{x_1(y_2-2)-x_2(y_1-2)}=\frac{(4-4y_1^2)(y_2-2)^2-(4-4y_2^2)(y_1-2)^2}{2(y_2-y_1)}=10(y_1+y_2)-8-8y_1y_2 x 1 ( y 2 − 2 ) + x 2 ( y 1 − 2 ) = x 1 ( y 2 − 2 ) − x 2 ( y 1 − 2 ) x 1 2 ( y 2 − 2 ) 2 − x 2 2 ( y 1 − 2 ) 2 = 2 ( y 2 − y 1 ) ( 4 − 4 y 1 2 ) ( y 2 − 2 ) 2 − ( 4 − 4 y 2 2 ) ( y 1 − 2 ) 2 = 10 ( y 1 + y 2 ) − 8 − 8 y 1 y 2 即
x 1 y 2 + x 2 y 1 = 2 ( x 1 + x 2 ) + 10 ( y 1 + y 2 ) − 8 − 8 y 1 y 2 x_1y_2+x_2y_1=2(x_1+x_2)+10(y_1+y_2)-8-8y_1y_2 x 1 y 2 + x 2 y 1 = 2 ( x 1 + x 2 ) + 10 ( y 1 + y 2 ) − 8 − 8 y 1 y 2 ①
同理有
( x 1 − 2 ) y 2 − ( x 2 − 2 ) y 1 = − 2 ( x 2 − x 1 ) (x_1-2)y_2-(x_2-2)y_1=-2(x_2-x_1) ( x 1 − 2 ) y 2 − ( x 2 − 2 ) y 1 = − 2 ( x 2 − x 1 ) ( x 1 − 2 ) y 2 − ( x 2 − 2 ) y 1 = ( x 1 − 2 ) 2 y 2 2 − ( x 2 − 2 ) 2 y 1 2 ( x 1 − 2 ) y 2 − ( x 2 − 2 ) y 1 = ( x 1 − 2 ) 2 ( 1 − x 2 2 4 ) − ( x 2 − 2 ) 2 ( 1 − x 1 2 4 ) − 2 ( x 2 − x 1 ) (x_1-2)y_2-(x_2-2)y_1=\frac{(x_1-2)^2y_2^2-(x_2-2)^2y_1^2}{(x_1-2)y_2-(x_2-2)y_1}=\frac{(x_1-2)^2(1-\frac{x_2^2}{4})-(x_2-2)^2(1-\frac{x_1^2}{4})}{-2(x_2-x_1)} ( x 1 − 2 ) y 2 − ( x 2 − 2 ) y 1 = ( x 1 − 2 ) y 2 − ( x 2 − 2 ) y 1 ( x 1 − 2 ) 2 y 2 2 − ( x 2 − 2 ) 2 y 1 2 = − 2 ( x 2 − x 1 ) ( x 1 − 2 ) 2 ( 1 − 4 x 2 2 ) − ( x 2 − 2 ) 2 ( 1 − 4 x 1 2 ) 即
x 1 y 2 + x 2 y 1 = ( x 1 + x 2 ) + 2 ( y 1 + y 2 ) − 2 − 1 2 x 1 x 2 x_1y_2+x_2y_1=(x_1+x_2)+2(y_1+y_2)-2-\frac{1}{2}x_1x_2 x 1 y 2 + x 2 y 1 = ( x 1 + x 2 ) + 2 ( y 1 + y 2 ) − 2 − 2 1 x 1 x 2 ②
两式比对系数凑配出
8 y 1 y 2 − 2 x 1 x 2 8y_1y_2-2x_1x_2 8 y 1 y 2 − 2 x 1 x 2 和目标式比对:
4 × 4\times 4 × ②
− - − ① 得
2 ( y 1 + y 2 ) − 2 ( x 1 + x 2 ) = 8 y 1 y 2 − 2 x 1 x 2 − 3 ( x 1 y 2 + x 2 y 1 ) 2(y_1+y_2)-2(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1) 2 ( y 1 + y 2 ) − 2 ( x 1 + x 2 ) = 8 y 1 y 2 − 2 x 1 x 2 − 3 ( x 1 y 2 + x 2 y 1 ) 对比
5 m ( y 1 + y 2 ) − 5 m ( x 1 + x 2 ) = 8 y 1 y 2 − 2 x 1 x 2 − 3 ( x 1 y 2 + x 2 y 1 ) 5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1) 5 m ( y 1 + y 2 ) − 5 m ( x 1 + x 2 ) = 8 y 1 y 2 − 2 x 1 x 2 − 3 ( x 1 y 2 + x 2 y 1 ) 得
m = 2 5 m=\frac{2}{5} m = 5 2 时恒成立。
故定点为
( 2 5 , 2 5 ) (\frac{2}{5},\frac{2}{5}) ( 5 2 , 5 2 ) 。
双曲线
概念:平面内到两个焦点 F 1 , F 2 F_1,F_2 F 1 , F 2 ∣ F 1 F 2 ∣ |F_1F_2| ∣ F 1 F 2 ∣
双曲线就是下列点的集合
P = { M ∣ ∣ ∣ M F 1 ∣ − ∣ M F 2 ∣ ∣ = 2 a } P=\set{M|||MF_1|-|MF_2||=2a} P = { M ∣ ∣∣ M F 1 ∣ − ∣ M F 2 ∣∣ = 2 a } ,
∣ F 1 F 2 ∣ = 2 c > 2 a |F_1F_2|=2c>2a ∣ F 1 F 2 ∣ = 2 c > 2 a 。
标准方程 x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\\ a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) x x x y 2 a 2 − x 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0) a 2 y 2 − b 2 x 2 = 1 ( a > 0 , b > 0 ) y y y 顶点坐标 ( ± a , 0 ) (\pm a,0) ( ± a , 0 ) ( 0 , ± a ) (0,\pm a) ( 0 , ± a ) 焦点坐标 ( ± c , 0 ) (\pm c,0) ( ± c , 0 ) ( 0 , ± c ) (0,\pm c) ( 0 , ± c ) 渐近线方程 y = ± b a x y=\pm\frac{b}{a}x y = ± a b x y = ± a b x y=\pm\frac{a}{b}x y = ± b a x
c 2 = a 2 + b 2 \boxed{c^2=a^2+b^2} c 2 = a 2 + b 2 e = c a ( e > 1 ) \boxed{e=\frac{c}{a}}\ (e>1) e = a c ( e > 1 )
实轴长
= 2 a =2a = 2 a 虚轴长
= 2 b =2b = 2 b 。
一般方程:
A x 2 + B y 2 = 1 ( A B < 0 ) Ax^2+By^2=1(AB<0) A x 2 + B y 2 = 1 ( A B < 0 ) 。
双曲线与它的渐近线无限接近但永不相交,求渐近线方程时,只要令
x 2 a 2 − y 2 b 2 = 0 \frac{x^2}{a^2}-\frac{y^2}{b^2}=0 a 2 x 2 − b 2 y 2 = 0 即可。
第二定义:平面内动点
M M M 到定点
F F F 的距离和它到准线
l : x = ± a 2 c l:x=\pm\frac{a^2}{c} l : x = ± c a 2 的距离之比等于
e e e 。
与两定点 A 1 ( − a , 0 ) , A 2 ( a , 0 ) ( a ≠ 0 ) A_1(-a,0),A_2(a,0)(a\neq 0) A 1 ( − a , 0 ) , A 2 ( a , 0 ) ( a = 0 ) b 2 a 2 = e 2 − 1 \frac{b^2}{a^2}=e^2-1 a 2 b 2 = e 2 − 1
双曲线焦点三角形的性质 双曲线
x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0) a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) 上异于顶点的点
P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) 与两焦点构成的
Δ P F 1 F 2 \Delta PF_1F_2 Δ P F 1 F 2 叫做焦点三角形。
以下记
∠ F 1 P F 2 = θ \angle F_1PF_2=\theta ∠ F 1 P F 2 = θ 。
面积
S = b 2 tan θ 2 = c ∣ y 0 ∣ \boxed{S=\frac{b^2}{\tan\frac{\theta}{2}}=c|y_0|} S = tan 2 θ b 2 = c ∣ y 0 ∣ 。
设
∠ P F 1 F 2 = α , ∠ P F 2 F 1 = β , P \angle PF_1F_2=\alpha,\angle PF_2F_1=\beta,P ∠ P F 1 F 2 = α , ∠ P F 2 F 1 = β , P 为双曲线右支上一点,则
∣ P F 1 ∣ sin β = ∣ P F 2 ∣ sin α = ∣ P F 1 ∣ − ∣ P F 2 ∣ sin β − sin α = 2 a sin β − sin α = ∣ F 1 F 2 ∣ sin ( α + β ) = 2 c sin θ \frac{|PF_1|}{\sin\beta}=\frac{|PF_2|}{\sin\alpha}=\frac{|PF_1|-|PF_2|}{\sin\beta-\sin\alpha}=\frac{2a}{\sin\beta-\sin\alpha}=\frac{|F_1F_2|}{\sin(\alpha+\beta)}=\frac{2c}{\sin\theta} s i n β ∣ P F 1 ∣ = s i n α ∣ P F 2 ∣ = s i n β − s i n α ∣ P F 1 ∣ − ∣ P F 2 ∣ = s i n β − s i n α 2 a = s i n ( α + β ) ∣ F 1 F 2 ∣ = s i n θ 2 c ,所以
e = sin ( α + β ) sin β − sin α \boxed{e=\frac{\sin(\alpha+\beta)}{\sin\beta-\sin\alpha}} e = sin β − sin α sin ( α + β ) 。
若焦点三角形内切圆的圆心为
I ( x 1 , y 1 ) I(x_1,y_1) I ( x 1 , y 1 ) ,与三边的切点分别为
M , N , R M,N,R M , N , R ,则
∣ F 1 R ∣ − ∣ F 2 R ∣ = ∣ F 1 M ∣ − ∣ F 2 N ∣ = ∣ P F 1 ∣ − ∣ P F 2 ∣ = 2 a |F_1R|-|F_2R|=|F_1M|-|F_2N|=|PF_1|-|PF_2|=2a ∣ F 1 R ∣ − ∣ F 2 R ∣ = ∣ F 1 M ∣ − ∣ F 2 N ∣ = ∣ P F 1 ∣ − ∣ P F 2 ∣ = 2 a ,即
c + x 1 − ( c − x 1 ) = 2 a c+x_1-(c-x_1)=2a c + x 1 − ( c − x 1 ) = 2 a ,解得
x 1 = a x_1=a x 1 = a 。
过双曲线焦点
( c , 0 ) (c,0) ( c , 0 ) 作渐近线
y = b a x y=\frac{b}{a}x y = a b x 的垂线,垂足长度为
b b b ,形成的三角形满足
a 2 + b 2 = c 2 a^2+b^2=c^2 a 2 + b 2 = c 2 。
双曲线的其它几何性质
通径:过双曲线
x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0) a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) 的焦点作垂直于实轴所在的直线,该直线被双曲线截得的弦叫做通径,长度为
2 b 2 a \frac{2b^2}{a} a 2 b 2 。
弦长公式:设直线
y = k x + m y=kx+m y = k x + m 与双曲线有两个公共点
M ( x 1 , y 1 ) , N ( x 2 , y 2 ) M(x_1,y_1),N(x_2,y_2) M ( x 1 , y 1 ) , N ( x 2 , y 2 ) ,则
∣ M N ∣ = ( 1 + k 2 ) [ ( x 1 + x 2 ) 2 − 4 x 1 x 2 ] = ( 1 + 1 k 2 ) [ ( y 1 + y 2 ) 2 − 4 y 1 y 2 ] |MN|=\sqrt{(1+k^2)[(x_1+x_2)^2-4x_1x_2]}=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]} ∣ MN ∣ = ( 1 + k 2 ) [( x 1 + x 2 ) 2 − 4 x 1 x 2 ] = ( 1 + k 2 1 ) [( y 1 + y 2 ) 2 − 4 y 1 y 2 ]
焦半径:双曲线一点
P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) 与左( 下 )焦点
F 1 F_1 F 1 或右( 上 )焦点
F 2 F_2 F 2 之间的线段叫做双曲线的焦半径,分别记作
r 1 = ∣ P F 1 ∣ , r 2 = ∣ P F 2 ∣ r_1=|PF_1|,r_2=|PF_2| r 1 = ∣ P F 1 ∣ , r 2 = ∣ P F 2 ∣ 。
x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0) a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) P P P r 1 = e x 0 + a , r 2 = e x 0 − a r_1=ex_0+a,r_2=ex_0-a r 1 = e x 0 + a , r 2 = e x 0 − a P P P r 1 = − e x 0 − a , r 2 = − e x 0 + a r_1=-ex_0-a,r_2=-ex_0+a r 1 = − e x 0 − a , r 2 = − e x 0 + a y 2 a 2 − x 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{y^2}{a^2}-\frac{x^2}{b^2}=1\ (a>0,b>0) a 2 y 2 − b 2 x 2 = 1 ( a > 0 , b > 0 ) P P P r 1 = e y 0 + a , r 2 = e y 0 − a r_1=ey_0+a,r_2=ey_0-a r 1 = e y 0 + a , r 2 = e y 0 − a P P P r 1 = − e y 0 − a , r 2 = − e y 0 + a r_1=-ey_0-a,r_2=-ey_0+a r 1 = − e y 0 − a , r 2 = − e y 0 + a
设
A B AB A B 是
x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0) a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) 的一条弦,
A B AB A B 中点为
M ( x 0 , y 0 ) M(x_0,y_0) M ( x 0 , y 0 ) ,则
k A B = b 2 x 0 a 2 y 0 k_{AB}=\frac{b^2x_0}{a^2y_0} k A B = a 2 y 0 b 2 x 0 ,
k A B k O M = e 2 − 1 \boxed{k_{AB}k_{OM}=e^2-1} k A B k OM = e 2 − 1 。
已知双曲线
x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0) a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) ,过双曲线的左焦点
F ( − c , 0 ) F(-c,0) F ( − c , 0 ) 的直线交双曲线于
A , B A,B A , B 两点,交
y y y 轴于点
P P P ,设
P F → = λ 1 F A → = λ 2 F B → \overrightarrow{PF}=\lambda_1\overrightarrow{FA}=\lambda_2\overrightarrow{FB} PF = λ 1 F A = λ 2 FB ,则
λ 1 + λ 2 = 2 e 2 1 − e 2 \lambda_1+\lambda_2=\frac{2e^2}{1-e^2} λ 1 + λ 2 = 1 − e 2 2 e 2
扩展:若
F F F 改为
x x x 轴上一点
M ( m , 0 ) M(m,0) M ( m , 0 ) ,则
λ 1 + λ 2 = 2 m 2 a 2 − m 2 \lambda_1+\lambda_2=\frac{2m^2}{a^2-m^2} λ 1 + λ 2 = a 2 − m 2 2 m 2 。
对于双曲线上一点
P P P 做切线交两条渐近线于
A , B A,B A , B ,则
S Δ P A B = a b S_{\Delta PAB}=ab S Δ P A B = ab
证明:
O A : x a 2 − y b 2 = 0 , O B : x a 2 + y b 2 = 0 , A B : x 0 x a 2 − y 0 y b 2 = 1 OA:\frac{x}{a^2}-\frac{y}{b^2}=0,OB:\frac{x}{a^2}+\frac{y}{b^2}=0,AB:\frac{x_0x}{a^2}-\frac{y_0y}{b^2}=1 O A : a 2 x − b 2 y = 0 , OB : a 2 x + b 2 y = 0 , A B : a 2 x 0 x − b 2 y 0 y = 1 设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , P ( x 0 , y 0 ) A(x_1,y_1),B(x_2,y_2),P(x_0,y_0) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) , P ( x 0 , y 0 ) ,分别代入得
x 0 x 1 a 2 − y 0 y 1 b 2 = 1 , x 0 x 2 a 2 − y 0 y 2 b 2 = 1 \frac{x_0x_1}{a^2}-\frac{y_0y_1}{b^2}=1,\frac{x_0x_2}{a^2}-\frac{y_0y_2}{b^2}=1 a 2 x 0 x 1 − b 2 y 0 y 1 = 1 , a 2 x 0 x 2 − b 2 y 0 y 2 = 1 代入
y 1 = b a x 1 , y 2 = − b a x 2 y_1=\frac{b}{a}x_1,y_2=-\frac{b}{a}x_2 y 1 = a b x 1 , y 2 = − a b x 2 得到
{ x 1 a ( x 0 a − y 0 b ) = 1 x 2 a ( x 0 a + y 0 b ) \begin{cases}\frac{x_1}{a}(\frac{x_0}{a}-\frac{y_0}{b})=1 \\ \frac{x_2}{a}(\frac{x_0}{a}+\frac{y_0}{b})\end{cases} { a x 1 ( a x 0 − b y 0 ) = 1 a x 2 ( a x 0 + b y 0 ) 相乘:
x 1 2 x 2 2 a 2 ( x 0 2 a 2 − y 0 2 b 2 ) = 1 ⟹ x 1 x 2 = a 2 , O A ⋅ O B = a 2 + b 2 a 2 x 1 x 2 = a 2 + b 2 = c 2 \frac{x_1^2x_2^2}{a^2}(\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2})=1\implies x_1x_2=a^2,OA\cdot OB=\frac{a^2+b^2}{a^2}x_1x_2=a^2+b^2=c^2 a 2 x 1 2 x 2 2 ( a 2 x 0 2 − b 2 y 0 2 ) = 1 ⟹ x 1 x 2 = a 2 , O A ⋅ OB = a 2 a 2 + b 2 x 1 x 2 = a 2 + b 2 = c 2 sin ∠ A O B = sin 2 ∠ A O x = 2 sin ∠ A O x cos ∠ A O x = 2 a b c 2 S = 1 2 O A ⋅ O B sin ∠ A O B = a b \sin\angle AOB=\sin 2\angle AOx=2\sin\angle AOx\cos\angle AOx=2\frac{ab}{c^2} \\ S=\frac{1}{2}OA\cdot OB\sin\angle AOB=ab sin ∠ A OB = sin 2∠ A O x = 2 sin ∠ A O x cos ∠ A O x = 2 c 2 ab S = 2 1 O A ⋅ OB sin ∠ A OB = ab
好题
若双曲线的一条渐近线过点 ( 8 , − 6 ) (8,-6) ( 8 , − 6 )
分
2 2 2 种情况讨论,焦点在
x x x 轴上(
b a = 3 4 e = 5 4 \frac{b}{a}=\frac{3}{4}\ \ \ e=\frac{5}{4} a b = 4 3 e = 4 5 ),在
y y y 轴上(
a b = 3 4 e = 5 3 \frac{a}{b}=\frac{3}{4}\ \ \ e=\frac{5}{3} b a = 4 3 e = 3 5 )
动圆 M M M C 1 : ( x + 4 ) 2 + y 2 = 1 C_1:(x+4)^2+y^2=1 C 1 : ( x + 4 ) 2 + y 2 = 1 C 2 : ( x − 4 ) 2 + y 2 = 9 C_2:(x-4)^2+y^2=9 C 2 : ( x − 4 ) 2 + y 2 = 9 M M M
解:圆
C 1 ( − 4 , 0 ) , r 1 = 1 , C 2 ( 4 , 0 ) , r 2 = 3 C_1(-4,0),r_1=1,C_2(4,0),r_2=3 C 1 ( − 4 , 0 ) , r 1 = 1 , C 2 ( 4 , 0 ) , r 2 = 3 ,设
M ( x , y ) M(x,y) M ( x , y ) ,半径为
r r r ,则
{ ∣ M C 1 ∣ = r + 1 ∣ M C 2 ∣ = r + 3 \begin{cases}
|MC_1|=r+1 \\
|MC_2|=r+3
\end{cases} { ∣ M C 1 ∣ = r + 1 ∣ M C 2 ∣ = r + 3 即
∣ M C 2 ∣ − ∣ M C 1 ∣ = 2 < ∣ C 1 C 2 ∣ |MC_2|-|MC_1|=2<|C_1C_2| ∣ M C 2 ∣ − ∣ M C 1 ∣ = 2 < ∣ C 1 C 2 ∣ ,所以
M M M 的轨迹为以
C 1 , C 2 C_1,C_2 C 1 , C 2 为焦点,
2 a = 2 2a=2 2 a = 2 的双曲线的
左支 ,
b = 15 b=\sqrt{15} b = 15 。
所以
M M M 的轨迹方程为
x 2 − y 2 15 = 1 ( x ≤ − 1 ) x^2-\frac{y^2}{15}=1\ (x\leq -1) x 2 − 15 y 2 = 1 ( x ≤ − 1 ) 。
是否存在过点 P ( 1 , − 1 2 ) P(1,-\frac{1}{2}) P ( 1 , − 2 1 ) l l l x 2 2 − y 2 = 1 \frac{x^2}{2}-y^2=1 2 x 2 − y 2 = 1 A , B A,B A , B P P P A B AB A B l l l
(
点差法 )解:设
l : y = k ( x − 1 ) − 1 2 , A ( x 1 , y 1 ) , B ( x 2 , y 2 ) l:y=k(x-1)-\frac{1}{2},A(x_1,y_1),B(x_2,y_2) l : y = k ( x − 1 ) − 2 1 , A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ,则
{ x 1 2 2 − y 1 2 = 1 x 2 2 2 − y 2 2 = 1 \begin{cases}
\frac{x_1^2}{2}-y_1^2=1 \\
\frac{x_2^2}{2}-y_2^2=1
\end{cases} { 2 x 1 2 − y 1 2 = 1 2 x 2 2 − y 2 2 = 1 ,
两式相减得
( x 1 − x 2 ) ( x 1 + x 2 ) = 2 ( y 1 − y 2 ) ( y 1 + y 2 ) (x_1-x_2)(x_1+x_2)=2(y_1-y_2)(y_1+y_2) ( x 1 − x 2 ) ( x 1 + x 2 ) = 2 ( y 1 − y 2 ) ( y 1 + y 2 ) ,因为
P ( 1 , − 1 2 ) P(1,-\frac{1}{2}) P ( 1 , − 2 1 ) 为线段
A B AB A B 的中点,则
x 1 + x 2 = 2 , y 1 + y 2 = − 1 , k = y 1 − y 2 x 1 − x 2 = x 1 + x 2 2 ( y 1 + y 2 ) = − 1 ⟹ l : y = − x + 1 2 x_1+x_2=2,y_1+y_2=-1,k=\frac{y_1-y_2}{x_1-x_2}=\frac{x_1+x_2}{2(y_1+y_2)}=-1\implies l:y=-x+\frac{1}{2} x 1 + x 2 = 2 , y 1 + y 2 = − 1 , k = x 1 − x 2 y 1 − y 2 = 2 ( y 1 + y 2 ) x 1 + x 2 = − 1 ⟹ l : y = − x + 2 1 联立
{ y = − x + 1 2 x 2 2 − y 2 = 1 \begin{cases}
y=-x+\frac{1}{2} \\
\frac{x^2}{2}-y^2=1
\end{cases} { y = − x + 2 1 2 x 2 − y 2 = 1 消去
y y y 可得
2 x 2 − 4 x + 5 = 0 , Δ < 0 2x^2-4x+5=0,\Delta<0 2 x 2 − 4 x + 5 = 0 , Δ < 0 ,方程无实根,故
l l l 不存在。
[ 安徽十校联盟 2023 期中 ] 已知双曲线
C : x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0) C : a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) 的左、右焦点分别为
F 1 , F 2 F_1,F_2 F 1 , F 2 ,焦距为
4 4 4 ,点
M M M 在圆
E : x 2 + y 2 + 4 x − 8 y + 16 = 0 E:x^2+y^2+4x-8y+16=0 E : x 2 + y 2 + 4 x − 8 y + 16 = 0 上,且
C C C 的一条渐近线上存在点
N N N ,使得四边形
O M N F 2 OMNF_2 OMN F 2 为平行四边形,
O O O 为坐标原点,则
C C C 的离心率的取值范围为( )
A. [ 2 , + ∞ ) B. [ 3 , + ∞ ) C. [ 4 , + ∞ ) D. ( 1 , 3 ) \text{A.} [2,+\infty)\ \ \ \ \ \ \text{B.} [\sqrt{3},+\infty)\ \ \ \ \ \ \text{C.} [4,+\infty)\ \ \ \ \ \ \text{D.} (1,\sqrt{3}) A. [ 2 , + ∞ ) B. [ 3 , + ∞ ) C. [ 4 , + ∞ ) D. ( 1 , 3 )
已知直线
y = a x + 1 y=ax+1 y = a x + 1 与双曲线
3 x 2 − y 2 = 1 3x^2-y^2=1 3 x 2 − y 2 = 1 交于
A , B A,B A , B 两点。
( 1 ) (1) ( 1 ) 若以
A B AB A B 为直径的圆过坐标原点
O O O ,求实数
a a a 的值。
( 2 ) (2) ( 2 ) 是否存在这样的实数
a a a ,使
A , B A,B A , B 两点关于直线
y = 1 2 x y=\frac{1}{2}x y = 2 1 x 对称?若存在,请求出
a a a 的值;若不存在,请说明理由。
解:
( 1 ) (1) ( 1 ) 联立
{ y = a x + 1 3 x 2 − y 2 = 1 \begin{cases}
y=ax+1\\
3x^2-y^2=1
\end{cases} { y = a x + 1 3 x 2 − y 2 = 1 消去
y y y 得
( 3 − a 2 ) x 2 − 2 a x − 2 = 0 (3-a^2)x^2-2ax-2=0 ( 3 − a 2 ) x 2 − 2 a x − 2 = 0 ,依题意
{ 3 − a 2 ≠ 0 Δ > 0 \begin{cases}
3-a^2\neq 0\\
\Delta >0
\end{cases}\\ { 3 − a 2 = 0 Δ > 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \text{} 解得
− 6 < a < 6 -\sqrt{6}<a<\sqrt{6} − 6 < a < 6 且
a ≠ ± 3 a\neq\pm\sqrt{3} a = ± 3 ,设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ,则
{ x 1 + x 2 = 2 a 3 − a 2 x 1 x 2 = − 2 3 − a 2 \begin{cases}
x_1+x_2=\frac{2a}{3-a^2} \\
x_1x_2=\frac{-2}{3-a^2}
\end{cases} { x 1 + x 2 = 3 − a 2 2 a x 1 x 2 = 3 − a 2 − 2 ∵ \ \ \ \ \ \ \ \ \ \ \ \ \ \because ∵ 以
A B AB A B 为直径的圆过坐标原点
O ∴ O A ⊥ O B , O A → ⋅ O B → = x 1 x 2 + y 1 y 2 = 0 ∵ y 1 y 2 = a 2 x 1 x 2 + a ( x 1 + x 2 ) + 1 O\ \ \ \therefore OA\perp OB,\ \overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=0\ \ \ \ \ \ \because y_1y_2=a^2x_1x_2+a(x_1+x_2)+1 O ∴ O A ⊥ OB , O A ⋅ OB = x 1 x 2 + y 1 y 2 = 0 ∵ y 1 y 2 = a 2 x 1 x 2 + a ( x 1 + x 2 ) + 1 ∴ x 1 x 2 + y 1 y 2 = ( a 2 + 1 ) x 1 x 2 + a ( x 1 + x 2 ) + 1 = ( a 2 + 1 ) ⋅ − 2 3 − a 2 + 2 a 2 3 − a 2 + 1 = 0 ⟹ a = ± 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore x_1x_2+y_1y_2=(a^2+1)x_1x_2+a(x_1+x_2)+1=(a^2+1)\cdot\frac{-2}{3-a^2}+\frac{2a^2}{3-a^2}+1=0\implies a=\pm 1 ∴ x 1 x 2 + y 1 y 2 = ( a 2 + 1 ) x 1 x 2 + a ( x 1 + x 2 ) + 1 = ( a 2 + 1 ) ⋅ 3 − a 2 − 2 + 3 − a 2 2 a 2 + 1 = 0 ⟹ a = ± 1 ( 2 ) \ \ \ \ \ \ \ (2) ( 2 ) 假设存在实数
a a a ,使
A , B A,B A , B 两点关于直线
y = 1 2 x y=\frac{1}{2}x y = 2 1 x 对称,则
a = − 2 a=-2 a = − 2 检验后可排除,故
a a a 不存在。
(
齐次化 )6. 已知
C : x 2 + y 2 = 4 C:x^2+y^2=4 C : x 2 + y 2 = 4 ,
A ( − 2 , 0 ) , B ( 2 , 0 ) A(-2,0),B(2,0) A ( − 2 , 0 ) , B ( 2 , 0 ) ,
P P P 在
x = 4 x=4 x = 4 上,
P A , P B PA,PB P A , PB 与
C C C 交于
M ( x 1 , y 1 ) , N ( x 2 , y 2 ) M(x_1,y_1),N(x_2,y_2) M ( x 1 , y 1 ) , N ( x 2 , y 2 ) ,求直线
M N MN MN 的定点?
解:设
P ( 4 , t ) ⟹ 3 k P A = k P B , M N : m y = x + t P(4,t)\implies 3k_{PA}=k_{PB},MN:my=x+t P ( 4 , t ) ⟹ 3 k P A = k PB , MN : m y = x + t ,因此
y 2 x 2 − 2 = 3 y 1 x 1 + 2 ⟹ y 2 m y 2 − ( t + 2 ) = 3 y 1 m y 1 + ( 2 − t ) ⟹ 2 m y 1 y 2 = ( 3 t + 6 ) ( y 1 + y 2 ) − ( 4 t + 4 ) y 2 ⟹ − 4 m ( t + 1 ) ( t + 2 ) m 2 + 1 = − 4 ( t + 1 ) y 2 \frac{y_2}{x_2-2}=\frac{3y_1}{x_1+2}\implies\frac{y_2}{my_2-(t+2)}=\frac{3y_1}{my_1+(2-t)}\implies 2my_1y_2=(3t+6)(y_1+y_2)-(4t+4)y_2\implies \frac{-4m(t+1)(t+2)}{m^2+1}=-4(t+1)y_2 x 2 − 2 y 2 = x 1 + 2 3 y 1 ⟹ m y 2 − ( t + 2 ) y 2 = m y 1 + ( 2 − t ) 3 y 1 ⟹ 2 m y 1 y 2 = ( 3 t + 6 ) ( y 1 + y 2 ) − ( 4 t + 4 ) y 2 ⟹ m 2 + 1 − 4 m ( t + 1 ) ( t + 2 ) = − 4 ( t + 1 ) y 2 所以
k P B k B M = − 3 k_{PB}k_{BM}=-3 k PB k BM = − 3 ,再设
y = k x + 3 … y=kx+3\dots y = k x + 3 …
设 F 1 , F 2 F_1,F_2 F 1 , F 2 C : x 2 a 2 − y 2 b 2 = 1 ( a > 0 , b > 0 ) C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0) C : a 2 x 2 − b 2 y 2 = 1 ( a > 0 , b > 0 ) A A A Δ A F 1 F 2 \Delta AF_1F_2 Δ A F 1 F 2 M M M a a a ∃ λ ∈ R , A M → + 2 O M → = λ O F 2 → \exist \lambda\in\R,\overrightarrow{AM}+2\overrightarrow{OM}=\lambda\overrightarrow{OF_2} ∃ λ ∈ R , A M + 2 OM = λ O F 2 C C C
得到
M ( a , a ) ⟹ A ( 3 a − λ c , 3 a ) , A F 2 = 2 c − a = e x A − a M(a,a)\implies A(3a-\lambda c,3a),AF_2=2c-a=ex_A-a M ( a , a ) ⟹ A ( 3 a − λ c , 3 a ) , A F 2 = 2 c − a = e x A − a ,因此
x A = 2 a , e = 2 x_A=2a,e=2 x A = 2 a , e = 2 抛物线
概念:平面内与一个定点 F F F l l l F F F
标准方程 y 2 = 2 p x ( p > 0 ) y^2=2px\ (p>0) y 2 = 2 p x ( p > 0 ) y 2 = − 2 p x ( p > 0 ) y^2=-2px\ (p>0) y 2 = − 2 p x ( p > 0 ) x 2 = 2 p y ( p > 0 ) x^2=2py\ (p>0) x 2 = 2 p y ( p > 0 ) x 2 = − 2 p y ( p > 0 ) x^2=-2py\ (p>0) x 2 = − 2 p y ( p > 0 ) 开口方向 向右 向左 向上 向下 焦点坐标 ( p 2 , 0 ) (\frac{p}{2},0) ( 2 p , 0 ) ( − p 2 , 0 ) (-\frac{p}{2},0) ( − 2 p , 0 ) ( 0 , p 2 ) (0,\frac{p}{2}) ( 0 , 2 p ) ( 0 , − p 2 ) (0,-\frac{p}{2}) ( 0 , − 2 p ) 准线 x = − p 2 x=-\frac{p}{2} x = − 2 p x = p 2 x=\frac{p}{2} x = 2 p y = − p 2 y=-\frac{p}{2} y = − 2 p y = p 2 y=\frac{p}{2} y = 2 p
通径:过抛物线的焦点作垂直于对称轴的直线,交抛物线于
A B AB A B ,线段
A B AB A B 就是抛物线的通径,长为
2 p 2p 2 p ,是所有过焦点的弦中最短的。
抛物线焦点弦的性质 A B AB A B 为过抛物线
y 2 = 2 p x ( p > 0 ) y^2=2px\ (p>0) y 2 = 2 p x ( p > 0 ) 的焦点
F ( p 2 , 0 ) F(\frac{p}{2},0) F ( 2 p , 0 ) 的弦,点
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) 在准线上的射影分别为点
A 1 ( − p 2 , y 1 ) , B 1 ( − p 2 , y 2 ) A_1(-\frac{p}{2},y_1),B_1(-\frac{p}{2},y_2) A 1 ( − 2 p , y 1 ) , B 1 ( − 2 p , y 2 ) 。
∣ A F ∣ = ∣ A A 1 ∣ = x 1 + p 2 , ∣ B F ∣ = ∣ B B 1 ∣ = x 2 + p 2 , ∣ A B ∣ = x 1 + x 2 + p |AF|=|AA_1|=x_1+\frac{p}{2},|BF|=|BB_1|=x_2+\frac{p}{2},|AB|=x_1+x_2+p ∣ A F ∣ = ∣ A A 1 ∣ = x 1 + 2 p , ∣ BF ∣ = ∣ B B 1 ∣ = x 2 + 2 p , ∣ A B ∣ = x 1 + x 2 + p 。
x 1 x 2 = p 2 4 , y 1 y 2 = − p 2 x_1x_2=\frac{p^2}{4},y_1y_2=-p^2 x 1 x 2 = 4 p 2 , y 1 y 2 = − p 2 。
证明:当直线
A B AB A B 的斜率存在时,设
A B : y = k ( x − p 2 ) , k ≠ 0 AB:y=k(x-\frac{p}{2}),k\neq 0 A B : y = k ( x − 2 p ) , k = 0 ,联立抛物线方程和直线方程得
y 2 − 2 p k y − p 2 = 0 y^2-\frac{2p}{k}y-p^2=0 y 2 − k 2 p y − p 2 = 0 。
易知
Δ > 0 \Delta>0 Δ > 0 ,所以
y 1 y 2 = − p 2 , x 1 x 2 = y 1 2 2 p y 2 2 2 p = p 2 4 y_1y_2=-p^2,x_1x_2=\frac{y_1^2}{2p}\frac{y_2^2}{2p}=\frac{p^2}{4} y 1 y 2 = − p 2 , x 1 x 2 = 2 p y 1 2 2 p y 2 2 = 4 p 2 ,同理可证直线
A B AB A B 的斜率不存在时,命题也成立。
以 ∣ A B ∣ |AB| ∣ A B ∣
证明:设
A B AB A B 中点为
D D D ,
D D D 到准线的距离为
d d d ,则
d = ∣ A A 1 ∣ + ∣ B B 1 ∣ 2 = ∣ A B ∣ 2 d=\frac{|AA_1|+|BB_1|}{2}=\frac{|AB|}{2} d = 2 ∣ A A 1 ∣ + ∣ B B 1 ∣ = 2 ∣ A B ∣ ,原命题得证。
以
∣ A F ∣ |AF| ∣ A F ∣ 为直径的圆与
y y y 轴相切。
1 ∣ A F ∣ + 1 ∣ B F ∣ = 2 p \frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p} ∣ A F ∣ 1 + ∣ BF ∣ 1 = p 2
证明:当直线
A B AB A B 的斜率存在时,
1 ∣ A F ∣ + 1 ∣ B F ∣ = 1 ∣ A A 1 ∣ + 1 ∣ B B 1 ∣ = 1 x + p 2 + 1 x 2 + p 2 = x 1 + x 2 + p x 1 x 2 + p 2 ( x 1 + x 2 ) + p 2 4 = x 1 + x 2 + p p 2 4 + p 2 ( x 1 + x 2 ) + p 2 4 = 2 p \frac{1}{|AF|}+\frac{1}{|BF|}=\frac{1}{|AA_1|}+\frac{1}{|BB_1|}=\frac{1}{x+\frac{p}{2}}+\frac{1}{x_2+\frac{p}{2}}=\frac{x_1+x_2+p}{x_1x_2+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{x_1+x_2+p}{\frac{p^2}{4}+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{2}{p} ∣ A F ∣ 1 + ∣ BF ∣ 1 = ∣ A A 1 ∣ 1 + ∣ B B 1 ∣ 1 = x + 2 p 1 + x 2 + 2 p 1 = x 1 x 2 + 2 p ( x 1 + x 2 ) + 4 p 2 x 1 + x 2 + p = 4 p 2 + 2 p ( x 1 + x 2 ) + 4 p 2 x 1 + x 2 + p = p 2 同理可证直线
A B AB A B 的斜率不存在时,命题也成立。
若直线 A B AB A B α \alpha α ∣ A B ∣ = 2 p sin 2 α |AB|=\frac{2p}{\sin^2\alpha} ∣ A B ∣ = s i n 2 α 2 p
证明:当直线
A B AB A B 的斜率存在时,设
A B : y = k ( x − p 2 ) , k ≠ 0 AB:y=k(x-\frac{p}{2}),k\neq 0 A B : y = k ( x − 2 p ) , k = 0 ,由
{ y = k ( x − p 2 ) y 2 = 2 p x \begin{cases} y=k(x-\frac{p}{2}) \\ y^2=2px\end{cases} { y = k ( x − 2 p ) y 2 = 2 p x 得
k y 2 − 2 p y − k p 2 = 0 ky^2-2py-kp^2=0 k y 2 − 2 p y − k p 2 = 0 。
易知
Δ > 0 , y 1 + y 2 = 2 p k , y 1 y 2 = − p 2 , ∣ A B ∣ = ( 1 + 1 k 2 ) [ ( y 1 + y 2 ) 2 − 4 y 1 y 2 ] = 1 + 1 k 2 ⋅ 2 p 1 + k 2 ∣ k ∣ = 2 p ( 1 + k 2 ) k 2 = 2 p ( 1 + tan 2 α ) tan 2 α = 2 p sin 2 α \Delta>0,y_1+y_2=\frac{2p}{k},y_1y_2=-p^2,|AB|=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}=\sqrt{1+\frac{1}{k^2}}\cdot\frac{2p\sqrt{1+k^2}}{|k|}=\frac{2p(1+k^2)}{k^2}=\frac{2p(1+\tan^2\alpha)}{\tan^2\alpha}=\frac{2p}{\sin^2\alpha} Δ > 0 , y 1 + y 2 = k 2 p , y 1 y 2 = − p 2 , ∣ A B ∣ = ( 1 + k 2 1 ) [( y 1 + y 2 ) 2 − 4 y 1 y 2 ] = 1 + k 2 1 ⋅ ∣ k ∣ 2 p 1 + k 2 = k 2 2 p ( 1 + k 2 ) = t a n 2 α 2 p ( 1 + t a n 2 α ) = s i n 2 α 2 p 当直线
A B AB A B 的斜率不存在时,
∣ A B ∣ = 2 p = 2 p sin 2 90 ° |AB|=2p=\frac{2p}{\sin^2 90\degree} ∣ A B ∣ = 2 p = s i n 2 90° 2 p ,命题也成立。
推广:
∣ A F ∣ = p 1 − cos α , ∣ B F ∣ = p 1 + cos α |AF|=\frac{p}{1-\cos\alpha},|BF|=\frac{p}{1+\cos\alpha} ∣ A F ∣ = 1 − c o s α p , ∣ BF ∣ = 1 + c o s α p ,
O O O 到
A B AB A B 的距离
= p sin α 2 , S Δ A O B = p 2 2 sin θ =\frac{p\sin\alpha}{2},S_{\Delta AOB}=\frac{p^2}{2\sin\theta} = 2 p s i n α , S Δ A OB = 2 s i n θ p 2 注:若抛物线为
x 2 = ± 2 p y x^2=\pm 2py x 2 = ± 2 p y ,将上述
cos \cos cos 换为
sin \sin sin ,
sin \sin sin 换为
cos \cos cos 。
A , O , B 1 A,O,B_1 A , O , B 1 A 1 , O , B A_1,O,B A 1 , O , B
设
A B : x = m y + p 2 AB:x=my+\frac{p}{2} A B : x = m y + 2 p 即可通过斜率相等证明。
A 1 F ⊥ B 1 F A_1F\perp B_1F A 1 F ⊥ B 1 F
对于
y 2 = 2 p x ( p > 0 ) y^2=2px(p>0) y 2 = 2 p x ( p > 0 ) ,当直线过点
( a , 0 ) (a,0) ( a , 0 ) 与抛物线交于
P , Q P,Q P , Q ,则
k O P k O Q = − 2 p a k_{OP}k_{OQ}=-\frac{2p}{a} k OP k OQ = − a 2 p 。
对于
y 2 = 2 p x y^2=2px y 2 = 2 p x ,
A B AB A B 为其一条弦,则
k A B = 2 p y 1 + y 2 k_{AB}=\frac{2p}{y_1+y_2} k A B = y 1 + y 2 2 p ;对于
x 2 = 2 p y x^2=2py x 2 = 2 p y ,则
k A B = x 1 + x 2 2 p k_{AB}=\frac{x_1+x_2}{2p} k A B = 2 p x 1 + x 2 。
对于
x 2 = 2 p y x^2=2py x 2 = 2 p y ,过其上一点
P ( x 1 , y 1 ) P(x_1,y_1) P ( x 1 , y 1 ) 做切线
y = k x + ( y 1 − k x 1 ) y=kx+(y_1-kx_1) y = k x + ( y 1 − k x 1 ) ,联立得
Δ = p k 2 − 2 x 1 k + 2 y 1 = 0 ⟹ k = x 1 p \Delta=pk^2-2x_1k+2y_1=0\implies k=\frac{x_1}{p} Δ = p k 2 − 2 x 1 k + 2 y 1 = 0 ⟹ k = p x 1 ,即切线为
y = x 1 p − x 1 2 2 p y=\frac{x_1}{p}-\frac{x_1^2}{2p} y = p x 1 − 2 p x 1 2 。
好题
过点 Q ( 4 , 1 ) Q(4,1) Q ( 4 , 1 ) y 2 = 8 x y^2=8x y 2 = 8 x A B AB A B Q Q Q A B AB A B
(
点差法 )解:设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ,则
{ y 1 2 = 8 x 1 ( 1 ) y 2 2 = 8 x 2 ( 2 ) \begin{cases} y_1^2=8x_1 (1) \\ y_2^2=8x_2 (2)\end{cases} { y 1 2 = 8 x 1 ( 1 ) y 2 2 = 8 x 2 ( 2 ) ,因为
Q ( 4 , 1 ) Q(4,1) Q ( 4 , 1 ) 是
A B AB A B 中点,所以
{ x 1 + x 2 = 8 y 1 + y 2 = 2 ( 3 ) \begin{cases} x_1+x_2=8 \\ y_1+y_2=2 \end{cases}(3) { x 1 + x 2 = 8 y 1 + y 2 = 2 ( 3 ) ( 1 ) − ( 2 ) (1)-(2) ( 1 ) − ( 2 ) 得
( y 1 + y 2 ) ( y 1 − y 2 ) = 8 ( x 1 − x 2 ) (y_1+y_2)(y_1-y_2)=8(x_1-x_2)\ \ \ \text{} ( y 1 + y 2 ) ( y 1 − y 2 ) = 8 ( x 1 − x 2 ) 把
( 3 ) (3) ( 3 ) 代入得
y 1 − y 2 x 1 − x 2 = 4 \frac{y_1-y_2}{x_1-x_2}=4 x 1 − x 2 y 1 − y 2 = 4 ,所以
A B : y = 4 x − 15 AB:y=4x-15 A B : y = 4 x − 15 。
已知抛物线 C : y 2 = 4 x C:y^2=4x C : y 2 = 4 x F F F l l l F F F C C C A , B A,B A , B A B AB A B y y y D , E D,E D , E ∣ D E ∣ = 4 5 ∣ A B ∣ |DE|=\frac{4}{5}|AB| ∣ D E ∣ = 5 4 ∣ A B ∣ l l l
解:设
∣ A B ∣ = 2 r ( 2 r ≥ 4 ) |AB|=2r(2r\geq 4) ∣ A B ∣ = 2 r ( 2 r ≥ 4 ) ,
A B AB A B 的中点为
M M M ,作
M N ⊥ y MN\perp y MN ⊥ y 轴于点
N N N ,过
A , B A,B A , B 分别作准线
l : x = − 1 l:x=-1 l : x = − 1 的垂线,垂足为
A 1 , B 1 A_1,B_1 A 1 , B 1 显然
2 ( ∣ M N ∣ + 1 ) = ∣ A A 1 ∣ + ∣ B B 1 ∣ = ∣ A F ∣ + ∣ B F ∣ = ∣ A B ∣ = 2 r 2(|MN|+1)=|AA_1|+|BB_1|=|AF|+|BF|=|AB|=2r 2 ( ∣ MN ∣ + 1 ) = ∣ A A 1 ∣ + ∣ B B 1 ∣ = ∣ A F ∣ + ∣ BF ∣ = ∣ A B ∣ = 2 r ,所以
∣ M N ∣ = r − 1 , ∣ D E ∣ = 2 r 2 − ( r − 1 ) 2 = 8 5 r |MN|=r-1,|DE|=2\sqrt{r^2-(r-1)^2}=\frac{8}{5}r ∣ MN ∣ = r − 1 , ∣ D E ∣ = 2 r 2 − ( r − 1 ) 2 = 5 8 r 解得
r = 5 2 or 5 8 r=\frac{5}{2}\ \text{or}\ \frac{5}{8} r = 2 5 or 8 5 ( 舍 ),所以
M x = 3 2 M_x=\frac{3}{2}\ \ \ \text{} M x = 2 3 设直线
l : y = k ( x − 1 ) , A ( x 1 , y 1 ) , B ( x 2 , y 2 ) l:y=k(x-1),A(x_1,y_1),B(x_2,y_2) l : y = k ( x − 1 ) , A ( x 1 , y 1 ) , B ( x 2 , y 2 ) 。
联立
{ y = k ( x − 1 ) y 2 = 4 x \begin{cases} y=k(x-1) \\ y^2=4x\end{cases} { y = k ( x − 1 ) y 2 = 4 x 得
k 2 x 2 − ( 2 k 2 + 4 ) x + k 2 = 0 ⟹ x 1 + x 2 = 2 k 2 + 4 k 2 = 3 k^2x^2-(2k^2+4)x+k^2=0\implies x_1+x_2=\frac{2k^2+4}{k^2}=3 k 2 x 2 − ( 2 k 2 + 4 ) x + k 2 = 0 ⟹ x 1 + x 2 = k 2 2 k 2 + 4 = 3 ,解得
k = ± 2 k=\pm 2 k = ± 2 。
故直线
l l l 的方程为
2 x ± y − 2 = 0 2x\pm y-2=0 2 x ± y − 2 = 0 。
( 多选 )已知点
F F F 是抛物线
y 2 = 2 p x ( p > 0 ) y^2=2px\ (p>0) y 2 = 2 p x ( p > 0 ) 的焦点,
A B , C D AB,CD A B , C D 是经过点
F F F 的弦,且
A B ⊥ C D AB\perp CD A B ⊥ C D ,直线
A B AB A B 的斜率为
k k k 且
k > 0 k>0 k > 0 ,
A , C A,C A , C 两点在
x x x 轴上方,以下一定成立的有( )
A. 1 ∣ A B ∣ + 1 ∣ C D ∣ = 1 2 p B. \text{A.}\ \frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{B.} A. ∣ A B ∣ 1 + ∣ C D ∣ 1 = 2 p 1 B. 若
∣ A F ∣ ⋅ ∣ B F ∣ = 4 3 p 2 |AF|\cdot|BF|=\frac{4}{3}p^2 ∣ A F ∣ ⋅ ∣ BF ∣ = 3 4 p 2 ,则
k = 3 3 k=\frac{\sqrt{3}}{3} k = 3 3 C. O A → ⋅ O B → = O C → ⋅ O D → D. \text{C.}\ \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OD}\ \ \ \ \ \ \ \ \text{D.} C. O A ⋅ OB = OC ⋅ O D D. 四边形
A C B D ACBD A CB D 面积的最小值为
16 p 2 16p^2 16 p 2
解析:
A. \text{A.} A. 由题得
k C D = − 1 k k_{CD}=-\frac{1}{k} k C D = − k 1 ,设
A B : y = k ( x − p 2 ) AB:y=k(x-\frac{p}{2}) A B : y = k ( x − 2 p ) ,联立
{ y = k ( x − p 2 ) y 2 = 2 p x \begin{cases} y=k(x-\frac{p}{2}) \\ y^2=2px\end{cases} { y = k ( x − 2 p ) y 2 = 2 p x 得
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{} k 2 x 2 − p ( k 2 + 2 ) x + 1 4 k 2 p 2 = 0 ⟹ x 1 + x 2 = p ( k 2 + 2 ) k 2 , x 1 x 2 = 1 4 p 2 ⟹ ∣ A B ∣ = x 1 + x 2 + p = 2 p ( k 2 + 1 ) k 2 k^2x^2-p(k^2+2)x+\frac{1}{4}k^2p^2=0\implies x_1+x_2=\frac{p(k^2+2)}{k^2},x_1x_2=\frac{1}{4}p^2\implies |AB|=x_1+x_2+p=\frac{2p(k^2+1)}{k^2} k 2 x 2 − p ( k 2 + 2 ) x + 4 1 k 2 p 2 = 0 ⟹ x 1 + x 2 = k 2 p ( k 2 + 2 ) , x 1 x 2 = 4 1 p 2 ⟹ ∣ A B ∣ = x 1 + x 2 + p = k 2 2 p ( k 2 + 1 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{} 同理
∣ C D ∣ = 2 p ( 1 + k 2 ) |CD|=2p(1+k^2) ∣ C D ∣ = 2 p ( 1 + k 2 ) ,则有
1 ∣ A B ∣ + 1 ∣ C D ∣ = 1 2 p \frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p} ∣ A B ∣ 1 + ∣ C D ∣ 1 = 2 p 1 \ \ \ \ \ \ \ \ \ \text{} B. \text{B.} B. ∣ A F ∣ ⋅ ∣ B F ∣ = ( x 1 + p 2 ) ( x 2 + p 2 ) = p 2 + p 2 k 2 = 4 3 p 2 ⟹ k = 3 |AF|\cdot|BF|=(x_1+\frac{p}{2})(x_2+\frac{p}{2})=p^2+\frac{p^2}{k^2}=\frac{4}{3}p^2\implies k=\sqrt{3} ∣ A F ∣ ⋅ ∣ BF ∣ = ( x 1 + 2 p ) ( x 2 + 2 p ) = p 2 + k 2 p 2 = 3 4 p 2 ⟹ k = 3 \ \ \ \ \ \ \ \ \ \text{} C. \text{C.} C. O A → ⋅ O B → = x 1 x 2 + y 1 y 2 = 1 4 p 2 + k 2 ( x 1 − p 2 ) ( x 2 − p 2 ) = − 3 4 p 2 \overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=\frac{1}{4}p^2+k^2(x_1-\frac{p}{2})(x_2-\frac{p}{2})=-\frac{3}{4}p^2 O A ⋅ OB = x 1 x 2 + y 1 y 2 = 4 1 p 2 + k 2 ( x 1 − 2 p ) ( x 2 − 2 p ) = − 4 3 p 2 ,与
k k k 无关,同理
O C → ⋅ O D → = − 3 4 p 2 \overrightarrow{OC}\cdot\overrightarrow{OD}=-\frac{3}{4}p^2 OC ⋅ O D = − 4 3 p 2 \ \ \ \ \ \ \ \ \ \text{} D. \text{D.} D. 因为
A B ⊥ C D AB\perp CD A B ⊥ C D 所以
S = 1 2 ∣ A B ∣ ⋅ ∣ C D ∣ = 1 2 2 p ( k 2 + 1 ) k 2 ⋅ 2 p ( 1 + k 2 ) = 2 p 2 ( k 2 + 1 k 2 + 2 ) ≥ 8 p 2 S=\frac{1}{2}|AB|\cdot|CD|=\frac{1}{2}\frac{2p(k^2+1)}{k^2}\cdot 2p(1+k^2)=2p^2(k^2+\frac{1}{k^2}+2)\geq 8p^2 S = 2 1 ∣ A B ∣ ⋅ ∣ C D ∣ = 2 1 k 2 2 p ( k 2 + 1 ) ⋅ 2 p ( 1 + k 2 ) = 2 p 2 ( k 2 + k 2 1 + 2 ) ≥ 8 p 2 当且仅当
k = 1 k=1 k = 1 取等。
(
同构 )4. (
2011 2011 2011 浙江卷 )已知抛物线
C 1 : x 2 = y C_1:x^2=y C 1 : x 2 = y ,圆
C 2 : x 2 + ( y − 4 ) 2 = 1 C_2:x^2+(y-4)^2=1 C 2 : x 2 + ( y − 4 ) 2 = 1 的圆心为点
M M M 。已知
P P P 是抛物线
C 1 C_1 C 1 上的点( 异于原点 ),过点
P P P 作圆
C 2 C_2 C 2 的两条切线,分别交
C 1 C_1 C 1 于点
A , B A,B A , B ,若过点
M , P M,P M , P 两点的直线
l l l 垂直于
A B AB A B ,求直线
l l l 的方程。
设
P ( x 0 , x 0 2 ) , A ( x 1 , x 1 2 ) , B ( x 2 , x 2 2 ) P(x_0,x_0^2),A(x_1,x_1^2),B(x_2,x_2^2) P ( x 0 , x 0 2 ) , A ( x 1 , x 1 2 ) , B ( x 2 , x 2 2 ) ,则
k A B = x 1 + x 2 k_{AB}=x_1+x_2 k A B = x 1 + x 2 ,
P A : y − x 0 2 = ( x 1 + x 0 ) ( x − x 0 ) PA:y-x_0^2=(x_1+x_0)(x-x_0) P A : y − x 0 2 = ( x 1 + x 0 ) ( x − x 0 ) ,即
( x 1 + x 0 ) x − y − x 1 x 0 = 0 (x_1+x_0)x-y-x_1x_0=0 ( x 1 + x 0 ) x − y − x 1 x 0 = 0 。
从而
1 = ∣ 4 + x 1 x 0 ∣ ( x 1 + x 0 ) 2 + 1 1=\frac{|4+x_1x_0|}{\sqrt{(x_1+x_0)^2+1}} 1 = ( x 1 + x 0 ) 2 + 1 ∣4 + x 1 x 0 ∣ ,整理得
( 1 − x 0 2 ) x 1 2 − 6 x 1 x 0 + x 0 2 − 15 = 0 (1-x_0^2)x_1^2-6x_1x_0+x_0^2-15=0 ( 1 − x 0 2 ) x 1 2 − 6 x 1 x 0 + x 0 2 − 15 = 0 ,同理
( 1 − x 0 2 ) x 2 2 − 6 x 2 x 0 + x 0 2 − 15 = 0 (1-x_0^2)x_2^2-6x_2x_0+x_0^2-15=0 ( 1 − x 0 2 ) x 2 2 − 6 x 2 x 0 + x 0 2 − 15 = 0 。
显然
x 1 , x 2 x_1,x_2 x 1 , x 2 是方程
( 1 − x 0 2 ) x 2 − 6 x x 0 + x 0 2 − 15 = 0 (1-x_0^2)x^2-6xx_0+x_0^2-15=0 ( 1 − x 0 2 ) x 2 − 6 x x 0 + x 0 2 − 15 = 0 的两根,
x 1 + x 2 = 6 x 0 1 − x 0 2 = k A B x_1+x_2=\frac{6x_0}{1-x_0^2}=k_{AB} x 1 + x 2 = 1 − x 0 2 6 x 0 = k A B ,因为
k l = x 0 2 − 4 x 0 k_l=\frac{x_0^2-4}{x_0} k l = x 0 x 0 2 − 4 。
所以可以解得
x 0 2 = 23 5 , l : y = ± 3 115 115 x + 4 x_0^2=\frac{23}{5},l:y=\pm\frac{3\sqrt{115}}{115}x+4 x 0 2 = 5 23 , l : y = ± 115 3 115 x + 4 。
(
向量 )5. 已知抛物线
y = x 2 , A ( − 1 2 , 1 4 ) , B ( 3 2 , 9 4 ) y=x^2,A(-\frac{1}{2},\frac{1}{4}),B(\frac{3}{2},\frac{9}{4}) y = x 2 , A ( − 2 1 , 4 1 ) , B ( 2 3 , 4 9 ) ,抛物线上的
P ( x , y ) ( − 1 2 < x < 3 2 ) P(x,y)(-\frac{1}{2}<x<\frac{3}{2}) P ( x , y ) ( − 2 1 < x < 2 3 ) ,过点
B B B 作直线
A P AP A P 的垂线,垂足为
Q Q Q ,求
∣ P A ∣ ⋅ ∣ P Q ∣ |PA|\cdot|PQ| ∣ P A ∣ ⋅ ∣ PQ ∣ 的最大值。
设
A B AB A B 中点为
M ( 1 2 , 5 4 ) M(\frac{1}{2},\frac{5}{4}) M ( 2 1 , 4 5 ) ,从而
∣ P A ∣ ⋅ ∣ P Q ∣ = − P A → ⋅ P Q → = − P A → ⋅ ( P B → + B Q → ) = − P A → ⋅ P B → = ( P A → − P B → 2 ) 2 − ( P A → + P B → 2 ) 2 = 2 − ∣ P M ∣ 2 = ( x + 1 2 ) 3 ( 3 2 − x ) = 1 3 ( x + 1 2 ) ( x + 1 2 ) ( x + 1 2 ) ( 9 2 − 3 x ) ≤ 1 3 [ ( x + 1 2 ) + ( x + 1 2 ) + ( x + 1 2 ) + ( 9 2 − 3 x ) ) 4 ] 4 ≤ 27 16 |PA|\cdot|PQ|=-\overrightarrow{PA}\cdot\overrightarrow{PQ}=-\overrightarrow{PA}\cdot(\overrightarrow{PB}+\overrightarrow{BQ})=-\overrightarrow{PA}\cdot\overrightarrow{PB}=(\frac{\overrightarrow{PA}-\overrightarrow{PB}}{2})^2-(\frac{\overrightarrow{PA}+\overrightarrow{PB}}{2})^2=2-|PM|^2=(x+\frac{1}{2})^3(\frac{3}{2}-x)=\frac{1}{3}(x+\frac{1}{2})(x+\frac{1}{2})(x+\frac{1}{2})(\frac{9}{2}-3x)\leq \frac{1}{3}[\frac{(x+\frac{1}{2})+(x+\frac{1}{2})+(x+\frac{1}{2})+(\frac{9}{2}-3x))}{4}]^4\leq\frac{27}{16} ∣ P A ∣ ⋅ ∣ PQ ∣ = − P A ⋅ PQ = − P A ⋅ ( PB + BQ ) = − P A ⋅ PB = ( 2 P A − PB ) 2 − ( 2 P A + PB ) 2 = 2 − ∣ PM ∣ 2 = ( x + 2 1 ) 3 ( 2 3 − x ) = 3 1 ( x + 2 1 ) ( x + 2 1 ) ( x + 2 1 ) ( 2 9 − 3 x ) ≤ 3 1 [ 4 ( x + 2 1 ) + ( x + 2 1 ) + ( x + 2 1 ) + ( 2 9 − 3 x )) ] 4 ≤ 16 27 。
(
齐次化 )6. 抛物线
C : y 2 = 2 p x C:y^2=2px C : y 2 = 2 p x ,设
A , B A,B A , B 为抛物线上的点,
O A ⊥ O B OA\perp OB O A ⊥ OB ,证明
A B AB A B 过定点。
设
A B : m x + n y = 1 AB:mx+ny=1 A B : m x + n y = 1 ,联立
y 2 = 2 p x ( m x + n y ) ⟹ y 2 − 2 p n x y − 2 p m x 2 = 0 y^2=2px(mx+ny)\implies y^2-2pnxy-2pmx^2=0 y 2 = 2 p x ( m x + n y ) ⟹ y 2 − 2 p n x y − 2 p m x 2 = 0 ,同时除以
x 2 x^2 x 2 得:
( y x ) 2 − 2 p n y x − 2 p m = 0 ⟹ y 1 x 1 y 2 x 2 = − 2 p m = − 1 (\frac{y}{x})^2-2pn\frac{y}{x}-2pm=0\implies\frac{y_1}{x_1}\frac{y_2}{x_2}=-2pm=-1 ( x y ) 2 − 2 p n x y − 2 p m = 0 ⟹ x 1 y 1 x 2 y 2 = − 2 p m = − 1 ,得
2 p m = 1 2pm=1 2 p m = 1 ,因此定点为
( 2 p , 0 ) (2p,0) ( 2 p , 0 ) 。
其他问题 共焦点问题 已知
F 1 , F 2 F_1,F_2 F 1 , F 2 为椭圆( 离心率
e 1 e_1 e 1 )和双曲线( 离心率
e 2 e_2 e 2 )的公共焦点,
P P P 是一个公共点,
∠ F 1 P F 2 = θ \angle F_1PF_2=\theta ∠ F 1 P F 2 = θ ,则
sin 2 θ 2 e 1 2 + cos 2 θ 2 e 2 2 = 1 \boxed{\frac{\sin^2\frac{\theta}{2}}{e_1^2}+\frac{\cos^2\frac{\theta}{2}}{e_2^2}=1} e 1 2 sin 2 2 θ + e 2 2 cos 2 2 θ = 1 ,因此可以推出
e 1 e 2 ≥ 2 sin θ 2 cos θ 2 = sin θ e_1e_2\geq 2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=\sin\theta e 1 e 2 ≥ 2 sin 2 θ cos 2 θ = sin θ 。
极点极线问题 设圆锥曲线
C : A x 2 + B y 2 + C x y + D x + E y + F = 0 C:Ax^2+By^2+Cxy+Dx+Ey+F=0 C : A x 2 + B y 2 + C x y + D x + E y + F = 0 ,平面上任意一点
P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) ,则极点
P P P 关于
C C C 的极线方程是
A x 0 x + B y 0 y + C x 0 y + y 0 x 2 + D x 0 + x 2 + E y 0 + y 2 + F = 0 Ax_0x+By_0y+C\frac{x_0y+y_0x}{2}+D\frac{x_0+x}{2}+E\frac{y_0+y}{2}+F=0 A x 0 x + B y 0 y + C 2 x 0 y + y 0 x + D 2 x 0 + x + E 2 y 0 + y + F = 0 。也就是说:
x 2 , y 2 x^2,y^2 x 2 , y 2 x 0 x , y 0 y x_0x,y_0y x 0 x , y 0 y x y xy x y x 0 y + y 0 x 2 \frac{x_0y+y_0x}{2} 2 x 0 y + y 0 x x , y x,y x , y x 0 + x 2 , y 0 + y 2 \frac{x_0+x}{2},\frac{y_0+y}{2} 2 x 0 + x , 2 y 0 + y 常数项不变。
对于椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) ,
P P P 的极线方程为
x 0 x a 2 + y 0 y b 2 = 1 \boxed{\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1} a 2 x 0 x + b 2 y 0 y = 1 ;当
P P P 是焦点时,极线
= = = 准线,即
x = a 2 c x=\frac{a^2}{c} x = c a 2 极点
P P P 和极线
l l l 的【位置关系】满足:
P P P l l l P P P P P P P P P l l l P P P P P P l l l P P P C D : x = t y + m , C ( x 1 , y 1 ) , D ( x 2 , y 2 ) , N ( m , 0 ) CD:x=ty+m,C(x_1,y_1),D(x_2,y_2),N(m,0) C D : x = t y + m , C ( x 1 , y 1 ) , D ( x 2 , y 2 ) , N ( m , 0 ) y 1 + y 2 = − 2 b 2 m t a 2 + b 2 t 2 , y 1 y 2 = b 2 m 2 − a 2 b 2 a 2 + b 2 t 2 y_1+y_2=\frac{-2b^2mt}{a^2+b^2t^2},y_1y_2=\frac{b^2m^2-a^2b^2}{a^2+b^2t^2} y 1 + y 2 = a 2 + b 2 t 2 − 2 b 2 m t , y 1 y 2 = a 2 + b 2 t 2 b 2 m 2 − a 2 b 2
注意到
m ( y 1 + y 2 ) + 2 t y 1 y 2 = − 2 a 2 b 2 t a 2 + b 2 t 2 = a 2 m ( y 1 + y 2 ) \displaystyle m(y_1+y_2)+2ty_1y_2=\frac{-2a^2b^2t}{a^2+b^2t^2}=\frac{a^2}{m}(y_1+y_2) m ( y 1 + y 2 ) + 2 t y 1 y 2 = a 2 + b 2 t 2 − 2 a 2 b 2 t = m a 2 ( y 1 + y 2 ) 有
A C : x = x 1 + a y 1 y − a , B D : x = x 2 − a y 2 y + a AC:x=\frac{x_1+a}{y_1}y-a,BD:x=\frac{x_2-a}{y_2}y+a A C : x = y 1 x 1 + a y − a , B D : x = y 2 x 2 − a y + a ,联立得
t y 1 + m + a y 1 y − a = t y 2 + m − a y 2 y + a ⟹ m + a y 1 y − m − a y 2 y = 2 a \frac{ty_1+m+a}{y_1}y-a=\frac{ty_2+m-a}{y_2}y+a\implies\frac{m+a}{y_1}y-\frac{m-a}{y_2}y=2a y 1 t y 1 + m + a y − a = y 2 t y 2 + m − a y + a ⟹ y 1 m + a y − y 2 m − a y = 2 a y M = 2 a y 1 y 2 m ( y 2 − y 1 ) + a ( y 1 + y 2 ) x M = a 2 ( y 2 − y 1 ) + 2 a t y 1 y 2 + a m ( y 1 + y 2 ) m ( y 2 − y 1 ) + a ( y 1 + y 2 ) = a 2 ( y 2 − y 1 ) + a ⋅ a 2 m ( y 1 + y 2 ) m ( y 2 − y 1 ) + a ( y 1 + y 2 ) = a 2 m \begin{aligned}y_M&=\frac{2ay_1y_2}{m(y_2-y_1)+a(y_1+y_2)}\\x_M&=\frac{a^2(y_2-y_1)+2aty_1y_2+am(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}\\&=\frac{a^2(y_2-y_1)+a\cdot\frac{a^2}{m}(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}=\frac{a^2}{m}\end{aligned} y M x M = m ( y 2 − y 1 ) + a ( y 1 + y 2 ) 2 a y 1 y 2 = m ( y 2 − y 1 ) + a ( y 1 + y 2 ) a 2 ( y 2 − y 1 ) + 2 a t y 1 y 2 + am ( y 1 + y 2 ) = m ( y 2 − y 1 ) + a ( y 1 + y 2 ) a 2 ( y 2 − y 1 ) + a ⋅ m a 2 ( y 1 + y 2 ) = m a 2 【性质】
过
P P P 作直线
P Q PQ PQ ,交极线
M N MN MN 于
Q Q Q ,交椭圆于
A , B A,B A , B 两点
⟺ ∣ P A ∣ ∣ P B ∣ = ∣ Q A ∣ ∣ Q B ∣ \iff\frac{|PA|}{|PB|}=\frac{|QA|}{|QB|} ⟺ ∣ PB ∣ ∣ P A ∣ = ∣ QB ∣ ∣ Q A ∣ ( 调和点列 )。
【例题】
设
C : x 2 4 + y 2 3 = 1 C:\frac{x^2}{4}+\frac{y^2}{3}=1 C : 4 x 2 + 3 y 2 = 1 ,过
C C C 的右焦点,且斜率不为
0 0 0 的直线交
C C C 于
M , N M,N M , N 两点,直线
A M , B N AM,BN A M , BN 交于点
Q Q Q ,证明:点
Q Q Q 在直线
x = 4 x=4 x = 4 上。
解:显然右焦点
( 1 , 0 ) (1,0) ( 1 , 0 ) 是极点,那么极线就是
x 4 = 1 \frac{x}{4}=1 4 x = 1 ,即
x = 4 x=4 x = 4 。
与定值 2 e \frac{2}{e} e 2
若 A B AB A B x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) F F F A B AB A B x x x M M M ∣ A B ∣ ∣ F M ∣ \frac{|AB|}{|FM|} ∣ FM ∣ ∣ A B ∣ 2 e \frac{2}{e} e 2
证明:设
F F F 为左焦点,以
F F F 为极点,
x x x 轴为极轴建立极坐标系,得极坐标方程
ρ = e p 1 − e cos θ \rho = \frac{ep}{1-e\cos\theta} ρ = 1 − e c o s θ e p ,
所以
∣ A B ∣ = ρ 1 + ρ 2 = 2 e p 1 − e 2 cos 2 θ |AB|=\rho_1+\rho_2=\frac{2ep}{1-e^2\cos^2\theta} ∣ A B ∣ = ρ 1 + ρ 2 = 1 − e 2 c o s 2 θ 2 e p ,
∣ F M ∣ = 1 ∣ cos θ ∣ ∣ ρ 1 − ρ 2 2 ∣ = e 2 p 1 − e 2 cos 2 θ ⟹ ∣ A B ∣ ∣ F M ∣ = 2 e |FM|=\frac{1}{|\cos\theta|}|\frac{\rho_1-\rho_2}{2}|=\frac{e^2p}{1-e^2\cos^2\theta}\implies\frac{|AB|}{|FM|}=\frac{2}{e} ∣ FM ∣ = ∣ c o s θ ∣ 1 ∣ 2 ρ 1 − ρ 2 ∣ = 1 − e 2 c o s 2 θ e 2 p ⟹ ∣ FM ∣ ∣ A B ∣ = e 2
椭圆 x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) F F F x x x F F F A A A F A FA F A R R R x x x N , M N,M N , M ∣ F M ∣ + ∣ F N ∣ R = 2 e \frac{|FM|+|FN|}{R}=\frac{2}{e} R ∣ FM ∣ + ∣ FN ∣ = e 2
证明:设圆为
[ x − ( R − c ) ] 2 + y 2 = R 2 [x-(R-c)]^2+y^2=R^2 [ x − ( R − c ) ] 2 + y 2 = R 2 ,联立得
x 1 + x 2 = 2 a 2 ( R − c ) c 2 , ∣ F M ∣ + ∣ F N ∣ = a + e x 1 + a + e x 2 = 2 R e x_1+x_2=\frac{2a^2(R-c)}{c^2},|FM|+|FN|=a+ex_1+a+ex_2=\frac{2R}{e} x 1 + x 2 = c 2 2 a 2 ( R − c ) , ∣ FM ∣ + ∣ FN ∣ = a + e x 1 + a + e x 2 = e 2 R
若 A B AB A B x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) F F F F M FM FM F F F ∣ A B ∣ ∣ F M ∣ ∣ F A ∣ ∣ F B ∣ = 2 e \frac{|AB||FM|}{|FA||FB|}=\frac{2}{e} ∣ F A ∣∣ FB ∣ ∣ A B ∣∣ FM ∣ = e 2
证明:同 1 建极坐标系,
∣ F M ∣ = p , ∣ F A ∣ = e p 1 − e cos θ , ∣ F B ∣ = e p 1 + e cos θ , ∣ A B ∣ = ∣ F A ∣ + ∣ F B ∣ = 2 e p 1 − e 2 cos 2 θ , ∣ F A ∣ ∣ F B ∣ = e 2 p 2 1 − e 2 cos 2 θ |FM|=p,|FA|=\frac{ep}{1-e\cos\theta},|FB|=\frac{ep}{1+e\cos\theta},|AB|=|FA|+|FB|=\frac{2ep}{1-e^2\cos^2\theta},|FA||FB|=\frac{e^2p^2}{1-e^2\cos^2\theta} ∣ FM ∣ = p , ∣ F A ∣ = 1 − e c o s θ e p , ∣ FB ∣ = 1 + e c o s θ e p , ∣ A B ∣ = ∣ F A ∣ + ∣ FB ∣ = 1 − e 2 c o s 2 θ 2 e p , ∣ F A ∣∣ FB ∣ = 1 − e 2 c o s 2 θ e 2 p 2 。
已知椭圆 x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) F 1 , F 2 , A ( − a , 0 ) , B ( a , 0 ) F_1,F_2,A(-a,0),B(a,0) F 1 , F 2 , A ( − a , 0 ) , B ( a , 0 ) P P P A , B A,B A , B ∠ A P B = 2 α , ∠ F 1 P F 2 = 2 β , ∣ tan β tan 2 α ∣ \angle APB=2\alpha,\angle F_1PF_2=2\beta,|\tan\beta\tan 2\alpha| ∠ A PB = 2 α , ∠ F 1 P F 2 = 2 β , ∣ tan β tan 2 α ∣ 2 e \frac{2}{e} e 2
光学性质 【椭圆】:设
F 1 , F 2 F_1,F_2 F 1 , F 2 是椭圆的两个焦点,从
F 1 F_1 F 1 出发的光线经过反射必经过
F 2 F_2 F 2 。
【双曲线】:设
F 1 , F 2 F_1,F_2 F 1 , F 2 是双曲线的两个焦点,从
F 1 F_1 F 1 出发的光线经过反射后的反向延长线必经过
F 2 F_2 F 2 。
【抛物线】:设
F F F 为焦点,从
F F F 出发的光线经过反射后,平行于对称轴。
【椭圆+抛物线】设
P P P 为反射点,
A B AB A B 为
P P P 处的切线,
P T PT PT 平分
∠ F 1 P F 2 \angle F_1PF_2 ∠ F 1 P F 2 ,则
P T ⊥ A B PT\perp AB PT ⊥ A B 仿射变换 设
a > 0 , b > 0 a>0,b>0 a > 0 , b > 0 ,将原来曲线上的每个点的横坐标乘以
a a a ,纵坐标乘以
b b b ,形成了新的曲线。
【性质】:
对原来的两条曲线作仿射变换,交点数不变。
对曲线 f ( x , y ) = 0 f(x,y)=0 f ( x , y ) = 0 f ( x a , y b ) = 0 f(\frac{x}{a},\frac{y}{b})=0 f ( a x , b y ) = 0
对面积为 S S S a b S abS ab S
对直线 A x + B y + C = 0 Ax+By+C=0 A x + B y + C = 0 A a x + B b y + C = 0 \frac{A}{a}x+\frac{B}{b}y+C=0 a A x + b B y + C = 0
【推论】
椭圆 x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) A x + B y + C = 0 Ax+By+C=0 A x + B y + C = 0 A 2 a 2 + B 2 b 2 = C 2 A^2a^2+B^2b^2=C^2 A 2 a 2 + B 2 b 2 = C 2
椭圆面积为 π a b \pi ab πab
阿基米德三角形 圆锥曲线的弦和过弦端点的两条切线所围成的三角形称为阿基米德三角形,该弦称为底边。
【2006高考卷】已知抛物线
x 2 = 4 y x^2=4y x 2 = 4 y 的焦点为
F F F ,点
A , B A,B A , B 是抛物线上两个动点,且
A F → = λ F B → ( λ > 0 ) \overrightarrow{AF}=\lambda\overrightarrow{FB}(\lambda>0) A F = λ FB ( λ > 0 ) ,过
A , B A,B A , B 两点分别作抛物线的切线,设其交点为
M M M ,证明:
F M → ⋅ A B → \overrightarrow{FM}\cdot\overrightarrow{AB} FM ⋅ A B 是定值。
解:设
A ( x 1 , x 1 2 4 ) , B ( x 2 , x 2 2 4 ) A(x_1,\frac{x_1^2}{4}),B(x_2,\frac{x_2^2}{4}) A ( x 1 , 4 x 1 2 ) , B ( x 2 , 4 x 2 2 ) ,由
A F → = λ F B → \overrightarrow{AF}=\lambda\overrightarrow{FB} A F = λ FB 得
x 1 x 2 = − 4 x_1x_2=-4 x 1 x 2 = − 4 。
已知抛物线方程为
y = 1 4 x 2 y=\frac{1}{4}x^2 y = 4 1 x 2 ,求导得
y ‘ = 1 2 x y`=\frac{1}{2}x y ‘ = 2 1 x ,所以过
A , B A,B A , B 两点的切线方程是
y = 1 2 x 1 x − 1 4 x 1 2 , y = 1 2 x 2 x − 1 4 x 2 2 y=\frac{1}{2}x_1x-\frac{1}{4}x_1^2,y=\frac{1}{2}x_2x-\frac{1}{4}x_2^2 y = 2 1 x 1 x − 4 1 x 1 2 , y = 2 1 x 2 x − 4 1 x 2 2 交点
M ( x 1 + x 2 2 , − 1 ) M(\frac{x_1+x_2}{2},-1) M ( 2 x 1 + x 2 , − 1 ) ,所以
F M → = ( x 1 + x 2 2 , − 2 ) , A B → = ( x 2 − x 1 , x 2 2 − x 1 2 4 ) \overrightarrow{FM}=(\frac{x_1+x_2}{2},-2),\overrightarrow{AB}=(x_2-x_1,\frac{x_2^2-x_1^2}{4}) FM = ( 2 x 1 + x 2 , − 2 ) , A B = ( x 2 − x 1 , 4 x 2 2 − x 1 2 ) ,从而
F M → ⋅ A B → = 0 \overrightarrow{FM}\cdot\overrightarrow{AB}=0 FM ⋅ A B = 0 扩展开来,对于抛物线
y 2 = 2 p x ( p > 0 ) y^2=2px(p>0) y 2 = 2 p x ( p > 0 ) 的焦点
F F F 的直线交抛物线于
A , B A,B A , B 两点,过
A , B A,B A , B 两点的切线交于
M M M ,则
F M → ⋅ A B → = 0 \boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0} FM ⋅ A B = 0 ,并且
M M M ,并且
∣ M F ∣ 2 = ∣ F A ∣ ⋅ ∣ F B ∣ \boxed{|MF|^2=|FA|\cdot|FB|} ∣ MF ∣ 2 = ∣ F A ∣ ⋅ ∣ FB ∣ 。( 证明
M A ⊥ M B MA\perp MB M A ⊥ MB 即可,射影定理 )
对于椭圆
x 2 a 2 + y 2 b 2 = 1 ( a > b > 0 ) \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) a 2 x 2 + b 2 y 2 = 1 ( a > b > 0 ) 的左焦点
F F F 任意做一条直线
A B AB A B ,交椭圆于
A , B A,B A , B 两点,分别过
A , B A,B A , B 作椭圆的切线交于点
M M M ,则
M M M ,且
F M → ⋅ A B → = 0 \boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0} FM ⋅ A B = 0 。( 通过设
A ( a cos θ 1 , b sin θ 1 ) A(a\cos\theta_1,b\sin\theta_1) A ( a cos θ 1 , b sin θ 1 ) 等证明 )
柯西不等式 引理 设
a → = ( x 1 , y 1 ) , b → = ( x 2 , y 2 ) \overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2) a = ( x 1 , y 1 ) , b = ( x 2 , y 2 ) ,由
∣ a → ∣ ⋅ ∣ b → ∣ ≥ a → ⋅ b → |\overrightarrow{a}|\cdot|\overrightarrow{b}|\geq\overrightarrow{a}\cdot\overrightarrow{b} ∣ a ∣ ⋅ ∣ b ∣ ≥ a ⋅ b 得
( x 1 2 + y 1 2 ) ⋅ ( x 2 2 + y 2 2 ) ≥ ( x 1 x 2 + y 1 y 2 ) 2 (x_1^2+y_1^2)\cdot(x_2^2+y_2^2)\geq(x_1x_2+y_1y_2)^2 ( x 1 2 + y 1 2 ) ⋅ ( x 2 2 + y 2 2 ) ≥ ( x 1 x 2 + y 1 y 2 ) 2 ,当且仅当
x 1 x 2 = y 1 y 2 \frac{x_1}{x_2}=\frac{y_1}{y_2} x 2 x 1 = y 2 y 1 时等号成立。
例题
设椭圆 C : x 2 16 + y 2 12 = 1 , M ( 2 , 2 ) C:\frac{x^2}{16}+\frac{y^2}{12}=1,M(2,\sqrt{2}) C : 16 x 2 + 12 y 2 = 1 , M ( 2 , 2 ) P ( − 8 , 0 ) P(-8,0) P ( − 8 , 0 ) C C C A , B A,B A , B Δ A B F \Delta ABF Δ A BF
设
A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ,由
P , A , B P,A,B P , A , B 三点共线得
k P A = k P B ⟹ y 1 x 1 + 8 = y 2 x 2 + 8 ⟹ x 2 y 1 − x 1 y 2 = 8 ( y 2 − y 1 ) k_{PA}=k_{PB}\implies\frac{y_1}{x_1+8}=\frac{y_2}{x_2+8}\implies x_2y_1-x_1y_2=8(y_2-y_1) k P A = k PB ⟹ x 1 + 8 y 1 = x 2 + 8 y 2 ⟹ x 2 y 1 − x 1 y 2 = 8 ( y 2 − y 1 ) S_{\Delta ABF}&=S_{\Delta PBF}-S_{\Delta PAF}=\frac{1}{2}|PF||y_1-y_2| \\
&=\frac{1}{2}\times 6\times |y_1-y_2|=\frac{3}{8}|x_1y_2-x_2y_1| \\
&\leq\frac{3}{8}\sqrt{12\times 16\times (\frac{x_1^2}{16}+\frac{y_1^2}{12})[\frac{y_2^2}{12}+\frac{(-x_2)^2}{16}]} \\
&=3\sqrt{3}
\end{aligned}$$
当且仅当 $\frac{x_1x_2}{4}=-\frac{y_1y_2}{3}$ 时成立。
2. 【天津静海四校 2021 阶段性检测】已知 $E:\frac{x^2}{4}+y^2=1,A(-2,0),B(0,1),F_1(-\sqrt{3},0),F_2(\sqrt{3},0),P$ 为椭圆上一动点。$C,D$ 是 $E$ 上两个不同的点,$CD//AB$,直线 $CD$ 与 $x,y$ 轴分别交于 $M,N$ 两点,且 $\overrightarrow{MC}=\lambda\overrightarrow{CN},\overrightarrow{MD}=\mu\overrightarrow{DN}$,求 $\lambda+\mu$ 的取值范围。
显然 $k_{AB}=\frac{1}{2}$,可设 $CD$ 的方程为 $y=\frac{1}{2}x+m(m\neq\pm 1)$,得 $M(-2m,0),N(0,m)$,设 $C(x_1,y_1),D(x_2,y_2)$
由 $\overrightarrow{MC}=\lambda\overrightarrow{CN}$,得 $(x_1+2m,y_1)=\lambda(-x_1,m-y_1)\implies\begin{cases}x_1=\frac{-2m}{1+\lambda} \\ y_1=\frac{\lambda m}{1+\lambda}\end{cases}$
代入椭圆方程并化简得 $(m^2-1)\lambda^2-2\lambda+m^2-1=0$,把 $\lambda$ 换成 $\mu$ 得到同构方程,因此 $\lambda,\mu$ 可看成 $(m^2-1)x^2-2x+m^2-1=0$ 的两根。
得到 $\lambda+\mu=\frac{2}{m^2-1}$,因为 $C,D$ 都在 $E$ 上,由柯西不等式
$$2=(\frac{x^2}{4}+y^2)[(-1)^2+1]\geq(-\frac{1}{2}x+y)^2=m^2$$
当且仅当 $C,D$ 重合时等号成立,与题意不符,故 $0\leq m^2<2$ 且 $m^2\neq 1$,所以 $\lambda+\mu=\frac{2}{m^2-1}\in(-\infty,-2]\cup(2,\infty)$
#### 拉格朗日恒等式
##### 椭圆形式的拉格朗日恒等式
设 $A(x_1,y_1),B(x_2,y_2)$ 是椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上非顶点的两点,则:
$$1=(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2})(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2})=(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})^2+\frac{(x_1y_2-x_2y_1)^2}{a^2b^2}$$
##### 引理 - 三角形面积公式
$\overrightarrow{OA}=(x_1,y_1),\overrightarrow{OB}=(x_2,y_2)$,则 $S_{\Delta OAB}=\frac{1}{2}|x_1y_2-x_2y_1|$
因此,拉格朗日恒等式可用于处理三角形面积定值问题。当 $(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})^2=0$ 时,$S_{\max}=\frac{ab}{2}$
##### 引理 - 和积关系 & 合比关系
已知 $A(x_1,y_1),B(x_2,y_2)$ 在椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上,直线 $AB$ 经过 $M(m,0)$ 满足:
$$2x_1x_2=(\frac{a^2}{m}+m)(x_1+x_2)-2a^2$$
直线 $AB$ 经过 $N(0,n)$ 满足:
$$2y_1y_2=(\frac{b^2}{n}+n)(y_1+y_2)-2b^2$$
可用点差法证明。
##### 例题
1. 椭圆 $E:\frac{x^2}{16}+\frac{y^2}{4}=1,P(0,1),Q(0,2)$,过点 $P$ 的直线 $l:y=kx+1$ 交椭圆 $E$ 于 $A,B$ 两点,求 $S_{\Delta ABQ}$ 最大值。
由 $A,B,P$ 三点共线得 $\frac{y_1-1}{x_1}=\frac{y_2-1}{x_2}$,得
$$(1)\ \ \ \ \ x_1y_2-x_2y_1=x_1-x_2$$
$$(2)\ \ \ \ \ 2y_1y_2=5(y_1+y_2)-8$$
$$(3)\ \ \ \ \ x_1x_2=-6(y_1+y_2)$$
由 $(y_1+y_2)^2-(y_1-y_2)^2=4y_1y_2$ 和 $(2)$ 得 $(y_1+y_2)^2-(y_1-y_2)^2=10(y_1+y_2)-16$
配方得 $(y_1+y_2-5)^2=9+(y_1-y_2)^2\geq 9$
所以 $y_1+y_2\leq 2$ 当且仅当 $y_1=y_2=1$ 时成立( $y_1+y_2\geq 8$ 舍去 )
由拉格朗日恒等式得
$$\begin{aligned}
1&=(\frac{x_1x_2}{16}+\frac{y_1y_2}{4})^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\
&=(\frac{y_1+y_2}{4}-1)^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\
&\geq \frac{1}{4}+\frac{(x_1y_2-x_2y_1)^2}{64}
\end{aligned}$$
得 $|x_1y_2-x_2y_1|\leq 4\sqrt{3}$,所以 $S=\frac{1}{2}|PQ||x_1-x_2|=\frac{1}{2}|x_1y_2-x_2y_1|\leq 2\sqrt{3}$
2. 已知椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$A,B$ 是其上两动点,$k_{OA}\cdot k_{OB}=-\frac{b^2}{a^2}$,点 $M$ 满足 $\overrightarrow{OM}=\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}$ 且 $\lambda^2+\mu^2=1$,证明 $M$ 在椭圆上。
设 $A(x_1,y_1),B(x_2,y_2)$,易得 $\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}=0$,点 $\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1,\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1$
因此 $M(\lambda x_1+\mu x_2,\lambda y_1+\mu y_2)$,代入椭圆方程联立得
$$\lambda^2(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2})+\mu^2(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2})+2\lambda\mu(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})=1$$
得到 $\lambda^2+\mu^2=1$,结论成立。( 每一步都是等价关系 )
#### 参数方程
| 曲线方程 | 参数方程 | 三角消元 |
|:-:|:-:|:-:|
| 直线 $y-y_0=\tan\alpha(x-x_0)(\alpha$ 为倾斜角 $)$ | $\begin{cases}x=x_0+t\cos\alpha \\ y=y_0+t\sin\alpha\end{cases}(t$ 为参数 $)$ | $P(x_0+t\cos\alpha,y_0+t\sin\alpha)$ |
| 圆 $(x-a)^2+(y-b)^2=r^2(r>0)$ | $\begin{cases}x=r\cos\alpha+a \\ y=r\sin\alpha+b\end{cases}(\alpha$ 为参数 $)$ | $P(r\cos\alpha+a,r\sin\alpha+b)$ |
| 椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ | $\begin{cases}x=a\cos\alpha \\ y=b\sin\alpha\end{cases}(\alpha$ 为参数 $)$ | $P(a\cos\alpha,b\sin\alpha)$ |
| 双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ | $\begin{cases}x=\frac{a}{\cos\alpha} \\ y=b\tan\alpha\end{cases}(\alpha$ 为参数 $)$ | $P(\frac{a}{\cos\alpha},b\tan\alpha)$ |
本质就是利用 $\sin^2\alpha+\cos^2\alpha=1$。
##### 例题
1. 过椭圆 $C:\frac{x^2}{4}+\frac{y^2}{9}=1$ 上一点 $P$ 作与直线 $l:2x+y-6=0$ 夹角为 $30\degree$ 的直线,交于 $A$,求 $|PA|$ 的最值。
设 $P(2\cos\theta,3\sin\theta)$,距离 $d(P,l)=\frac{\sqrt{5}}{5}|4\cos\theta+3\sin\theta-6|$,
则 $|PA|=\frac{d}{\sin 30\degree}=\frac{2\sqrt{5}}{5}|5\sin(\theta+\alpha)-6|$,其中 $\alpha$ 为锐角。所以最值为 $\frac{2\sqrt{5}}{5}$ 和 $\frac{22\sqrt{5}}{5}$。
2. 椭圆 $C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$A,B,C$ 为其上三点,满足 $\Delta ABC$ 的重心坐标为 $O$,求 $S_{\Delta ABC}$。
设 $A(a\cos\alpha,b\sin\alpha),B(a\cos\beta,b\sin\beta)\implies C(-a(\cos\alpha+\cos\beta),-b(\sin\alpha+\sin\beta))$,代入得
$(\cos\alpha+\cos\beta)^2+(\sin\alpha+\sin\beta)^2=2+2\cos\alpha\cos\beta+2\sin\alpha\sin\beta=2+2\cos(\alpha-\beta)=1\implies\cos(\alpha-\beta)=-\frac{1}{2}\implies\alpha-\beta=120\degree$
$|AB|=\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}$
$AB:y=\frac{b(\sin\alpha-\sin\beta)}{a(\cos\alpha-\cos\beta)}(x-a\cos\alpha)+b\sin\alpha\implies b(\sin\beta-\sin\alpha)x+a(\cos\alpha-\cos\beta)y+ab\sin(\alpha-\beta)=0$
$d(O,AB)=\frac{\frac{\sqrt{3}}{2}ab}{\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}}$
由重心性质,$S_{\Delta ABC}=3S_{\Delta AOB}=\frac{3}{2}|AB|d=\frac{3\sqrt{3}}{4}ab$。
- 扩展开来,对于平行四边形 $OABC$,其中 $A,B,C$ 三点都在椭圆上,则 $S=2S_{\Delta AOB}=\frac{\sqrt{3}}{2}ab$。 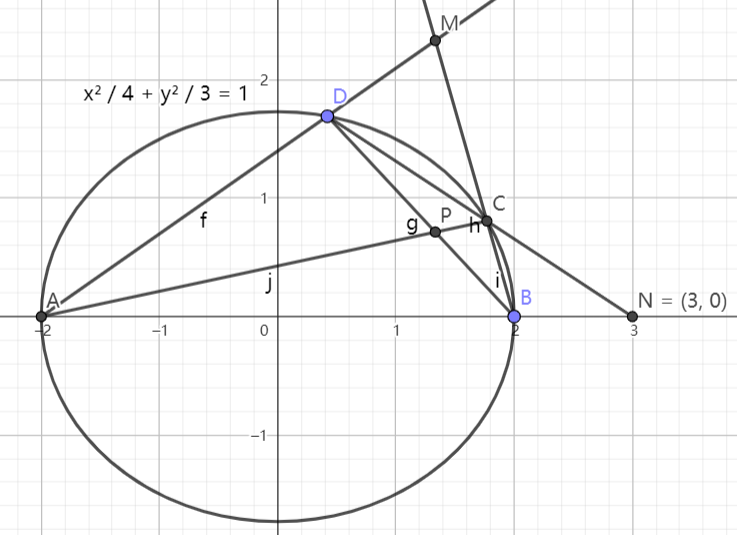 【部分证明】
设 ,则
【部分证明】
设 ,则