关于巴塞尔问题的一种证明

众所周知，$\sum\limits_{i=1}^\infty\dfrac{1}{i}=\infty$，也就是说 $\sum\limits_{i=1}^\infty\dfrac{1}{i}$ 这个级数是发散的，今天我们称其为调和级数。

而我们将在这篇文章中，讨论另一个级数 $\sum\limits_{i=1}^\infty\dfrac{1}{i^2}=\dfrac{\pi^2}{6}$ 的证明，即巴塞尔问题。

在物理学中，许多量与距离的关系呈现出“平方反比”的关系，如万有引力中 $F=\dfrac{Gm_1m_2}{r^2}$，库仑力中 $F=\dfrac{kq_1q_2}{r^2}$。

光照强度与距离同样也呈现出“平方反比”的关系。

感性理解一下，假设一个中心光源放出的光在一米处全部投射在一平方米的面积上，把距离拉至 $n$ 倍后，根据两平面位似的关系，我们容易知道此时投射面积为 $n^2$，但光的总量是不变的，故单位面积的光照强度缩小为原来的 $\dfrac{1}{n^2}$。

众所周知，在一个直角三角形中，假设两条直角边的长度分别为 $a$，$b$，斜边的长度为 $c$，则有 $a^2+b^2=c^2$，这就是大名鼎鼎的勾股定理。

我们坐这个直角三角形斜边上的高，记其长度为 $h$，容易知道 $S=\dfrac{ab}{2}=\dfrac{ch}{2}$，即 $ab=ch$，两边平方得 $a^2b^2=c^2h^2$，套用勾股定理有 $a^2b^2=(a^2+b^2)h^2$，取倒数得 $\dfrac{1}{a^2b^2}=\dfrac{1}{(a^2+b^2)h^2}$，两边同乘 $a^2+b^2$ 有 $\dfrac{a^2+b^2}{a^2b^2}=\dfrac{1}{h^2}$，即 $\dfrac{1}{a^2}+\dfrac{1}{b^2}=\dfrac{1}{h^2}$，即“倒数勾股定理”。

现在说了这么多，我们可以开始正式证明巴塞尔问题了。

假设你站在一个周长为 $2$ 的圆形湖泊的边缘某一点上，你的正对面有一座灯塔，用数学语言表达，也就是说过你和湖泊的圆心两点作一条直线，与湖泊交于另一点，灯塔就在这个点上。

现在考虑你的位置接收到的光照强度。因为湖泊周长为 $2$，所以湖泊的直径为 $\dfrac{2}{\pi}$，故光照强度为 $\dfrac{1}{(\dfrac{2}{\pi})^2}=\dfrac{\pi^2}{4}$。

接下来我们作一个大圆，周长为 $4$，也就是说这个圆是原先湖泊的两倍。

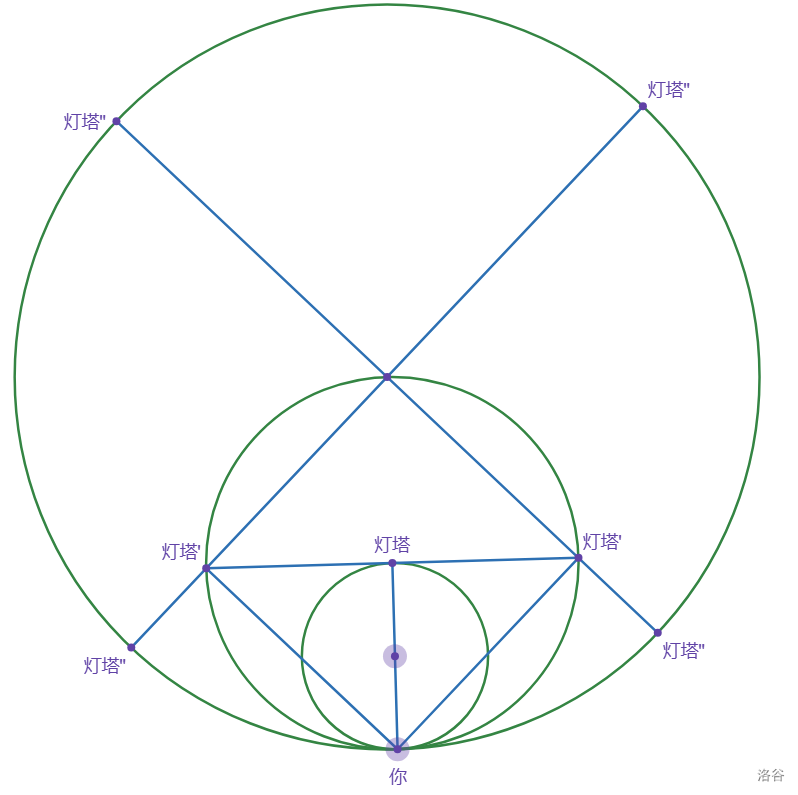
过灯塔做小圆的切线，与大圆交于两点，在这两点上分别放置灯塔'。

我们知道，两座灯塔'的连线过大圆的圆心（即灯塔），故我们知道两座灯塔'与你形成了一个等腰直角三角形，又因为两座灯塔'的连线与小圆相切，所以灯塔与你的连线与两座灯塔'的连线垂直。

这时候我们就可以用上倒数勾股定理，我们就可以知道这两座灯塔'的效果与原先的灯塔是等效的。

我们再作一个大大圆，直径是大圆的两倍。

再次将两座灯塔'与大圆圆心作连线，与大大圆有 $4$ 个交点，记为灯塔''。

同样的道理，我们可以知道四座灯塔''的效果仍与原灯塔等效！

不断重复将灯塔与圆心连线并与更大的圆相交于两点的操作，容易知道，这些灯塔的效果与原灯塔仍然等效，他们的光照强度总和仍为 $\dfrac{\pi^2}{4}$！

此外，我们可以容易知道，圆周上每座间的距离都为 $2$，且与你距离最近的灯塔与你的距离为 $1$。

在极限情况下，这个圆无限大，其下部可视为一条水平线，水平线上距离你为 $1$，$3$，$5$，……，$2k+1(k\in Z)$……的地方都有灯塔，并且他们的光照强度总和为 $\dfrac{\pi^2}{4}$！

由此我们知道 $2\sum\limits_{i=1}^\infty\dfrac{1}{(2i-1)^2}=\dfrac{\pi^2}{4}$，即 $\sum\limits_{i=1}^\infty\dfrac{1}{(2i-1)^2}=\dfrac{\pi^2}{8}$。

我们设 $\sum\limits_{i=1}^\infty\dfrac{1}{(2i)^2}=s$，则 $\sum\limits_{i=1}^\infty\dfrac{1}{(i)^2}=4s=\sum\limits_{i=1}^\infty\dfrac{1}{(2i)^2}+\sum\limits_{i=1}^\infty\dfrac{1}{(2i-1)^2}=s+\dfrac{\pi^2}{8}$。

故 $3s=\dfrac{\pi^2}{8}$，有 $s=\dfrac{\pi^2}{24}$。

故 $\sum\limits_{i=1}^\infty\dfrac{1}{(i)^2}=4s=\dfrac{\pi^2}{6}$，证毕！