题解：CF1425B Blue and Red of Our Faculty!

前置知识：缺一分治

考虑这样一个问题，01 背包，但是每次问你强制不选一个物品后的答案。考虑对这个不选的物品分治，每次处理不选物品在

[l,r]

时的答案，若

l=r

，则我们直接用上一层预处理出的背包数组去更新答案。否则我们干这样的事情：

将 $[l,mid]$ 中物品全部加入当前层的背包数组，递归 $[mid+1,r]$ 区间；
清空 $[l,mid]$ 中物品；
将 $[mid+1,r]$ 中物品全部加入当前层的背包数组，递归 $[l,mid]$ 区间；

也就是说，我们干的事情是加一侧、递归另一侧。因此当

l=r

处理答案时，此时的背包恰好涵盖了

[1,l)\cup (l,n]

的物品。

分析下复杂度，每层递归做背包的物品个数是

O(r-l+1)

的，因此不难证明是

O(nV\log n)

的。

考虑下这个图张什么样，大概是中间有个

1

号点，然后和若干个环拼起来。刻画一下每个环最终可能会被染成什么样，发现我们有五种染色方式：

该环全被染成红色或蓝色了。
该环根本没被染。
该环被划分成了两段，其中一部分被红色染了，另一部分被蓝色染了。
该环被划分成了三段，其中一部分被红色染了，一部分被蓝色染了，两部分中间存在一条灰边。
该环被划分成了两段，其中一部分被红色或蓝色染了，另一部分是灰边。

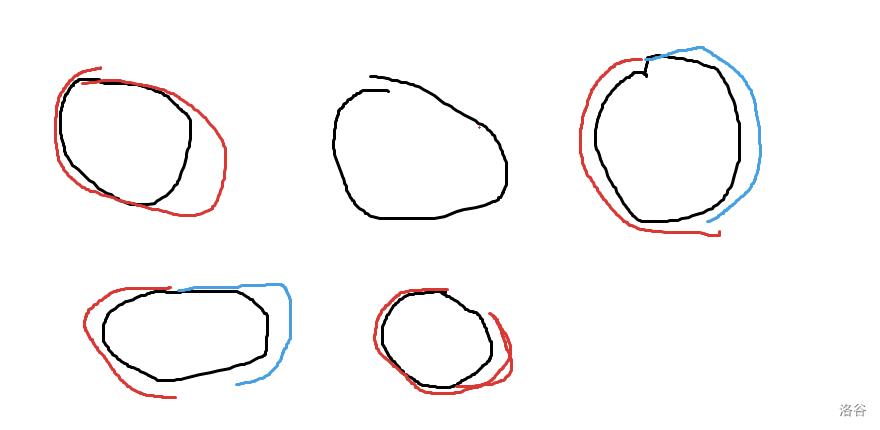
上图对应了这五种染色方式。

不妨考虑一下这五种染色方式是否真的都会存在。一个关键的性质是：用第三、四、五种染色方式的，至多有一个环。原因显然，因为当走到这些环内之后，移动必然会结束。

令

f_i

代表将每个环按照第一、二种方法染色，即全染或不染，目前蓝色边数与红色边数之差恰为

i

的方案数。转移显然，对于一个环长为

x

的环，可以选择不染、染成蓝的、染成红的，那么转移式为：

f'_i\leftarrow f_i+f_{i-x}+f_{i+x}

则我们要考虑的是去掉一个环之后剩下所有的环的

f_i

。这是一个经典的缺一分治模型，直接做就好了。

当然这个题细节非常多，比如当

l=r

时具体应该怎么处理答案，以及如何区分第三、四、五种染色方案。对于

l=r

时，我们枚举这个环中有

i

条蓝边，此时环中可以有

0

条红边（第五种）、

len-i

条红边（第三种）、

len-i-1

条红边（第四种），我们需要分别加上其对应的状态。

特别注意，对于

0

条红边的情况，有些方案是不合法的，因为红方还可以继续往别的未染色（第二种）的环里走，因此我们可以再令

g_i

代表强制不用第二种染色方案的方案，特殊处理一下即可。

下面给出参考代码。

CPP

#include<bits/stdc++.h>
using namespace std;
const int N=4005;
const int M=15;
const int mod=1e9+7;
#define int long long
int n,m,cnt,tot,ans;
int a[N],vis[N],f[N][M],f2[N][M],tmp[N],tmp2[N];
//f[i]: cntblue-cntred=i
vector<int> g[N];
void dfs(int u){
	vis[u]=1,cnt++;
	for(auto v:g[u]){
		if(!vis[v]){
			dfs(v);
		}
	}
}
void solve(int l,int r,int dep){
	if(l==r){
		for(int i=1;i<a[l];i++){
			if(i==a[l]-1){
				ans=(ans+2*f[a[l]-i-i+n][dep])%mod;
			}else{
				ans=(ans+2*(f[a[l]-i-i+n][dep]+f[a[l]-i-i+n-1][dep]))%mod;
			}
		}
		return;
	}
	int mid=(l+r)/2;
	for(int i=0;i<=n*2;i++){
		f[i][dep+1]=f[i][dep];
	}
	for(int i=l;i<=mid;i++){
		for(int j=0;j<=n*2;j++){
			tmp[j]=f[j][dep+1];
			if(j+a[i]<=n*2){
				tmp[j]=(tmp[j]+f[j+a[i]][dep+1])%mod;
			}
			if(j-a[i]>=0){
				tmp[j]=(tmp[j]+f[j-a[i]][dep+1])%mod;
			}
		}
		for(int j=0;j<=n*2;j++){
			f[j][dep+1]=tmp[j];
		}
	}
	solve(mid+1,r,dep+1);
	for(int i=0;i<=n*2;i++){
		f[i][dep+1]=f[i][dep];
	}
	for(int i=mid+1;i<=r;i++){
		for(int j=0;j<=n*2;j++){
			tmp[j]=f[j][dep+1];
			if(j+a[i]<=n*2){
				tmp[j]=(tmp[j]+f[j+a[i]][dep+1])%mod;
			}
			if(j-a[i]>=0){
				tmp[j]=(tmp[j]+f[j-a[i]][dep+1])%mod;
			}
		}
		for(int j=0;j<=n*2;j++){
			f[j][dep+1]=tmp[j];
		}
	}	
	solve(l,mid,dep+1);
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		g[u].push_back(v),g[v].push_back(u);
	}
	vis[1]=1;
	for(auto i:g[1]){
		if(!vis[i]){
			cnt=1,dfs(i),a[++tot]=cnt;
		}
	}
	f[n][0]=1;
	solve(1,tot,0);
	memset(f,0,sizeof(f));
	f[n][0]=1;
	for(int i=1;i<=tot;i++){
		for(int j=0;j<=n*2;j++){
			tmp[j]=tmp2[j]=0;
			if(j+a[i]<=n*2){
				tmp[j]=(tmp[j]+f[j+a[i]][0])%mod;
				tmp2[j]=(tmp2[j]+f2[j+a[i]][0])%mod;
			}
			if(j-a[i]>=0){
				tmp[j]=(tmp[j]+f[j-a[i]][0])%mod;
				tmp2[j]=(tmp2[j]+f2[j-a[i]][0])%mod;
			}
			if(j-(a[i]-1)>=0){
				tmp2[j]=(tmp2[j]+f[j-(a[i]-1)][0])%mod;
			}
			if(j+(a[i]-1)<=n*2){
				tmp2[j]=(tmp2[j]+f[j+(a[i]-1)][0])%mod;
			}
		}
		for(int j=0;j<=n*2;j++){
			f[j][0]=tmp[j];
			f2[j][0]=tmp2[j];
		}
	}
	cout<<(ans+f2[n][0]*2+f[n][0])%mod;
	return 0;
}

题解：CF1425B Blue and Red of Our Faculty!

文章操作

相关推荐

评论

题解：CF1425B Blue and Red of Our Faculty!