立体几何
弧度制与面积计算
-
360°=2π rad, 180°=π rad
-
1°=180π rad≈0.01745 rad,1 rad=(π180)°≈57.29578°
-
x°=180xπ rad,x rad=(π180x)°
-
圆心角大小( 弧度 )
∣α∣=rl 圆心角大小( 角度 )
n=rπ180⋅l
-
弧长
l=αr,周长
C=2r+l,面积
S=21αr2=21lr
基本立体图形
-
共性:都具有顶点、底面、侧面、侧棱( 相邻侧面的公共边 )。
-
棱柱:有
两个面相互平行,其余各面都是四边形,并且相邻两个四边形的公共边都相互平行。底面是
n 边形就叫
n 棱柱。斜高:侧面的高。
侧棱垂直于底面的柱叫做直棱柱,侧棱不垂直于底面的棱柱叫做斜柱。底面是正多边形的直棱柱叫做正棱柱,底面是平行四边形的四棱柱也叫做平行六面体。
{正方体}∈{正四棱柱}∈{长方体}∈{直四棱柱}
-
棱锥:三棱锥又叫四面体( 即由四个面组成的封闭图形只能是三棱锥 ),底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。
正三棱锥 / 正四面体的三条对棱两两垂直。
-
棱台:棱锥上部通过平行于底面的面截取上部且上下底面平行。
-
圆柱 / 圆锥 / 圆台:旋转轴称为它的轴,平行于轴的边叫做它侧面的母线。
-
欧拉公式:
V−E+F=2,即 顶点数
− 棱数
+ 面数
=2。
对于正
n 面体(
n 个等边三角形 ),面数为
n,棱数为
23n( 每个面
3 条棱,每条棱分属
2 个面 )。
立体图形的直观图
-
斜二测画法
∠xOy=90°x 轴不变∠x′Oy′=45° 或
135°,∠x′Oz′=∠xOz=90°,
原来平行于
x 轴 或 z 轴 的线段,在直观图中保持原长度不变,原来平行于
y 轴的线段,在直观图中长度变为原来的一半。
-
S直=42S原,S原=22S直
简单几何体的表面积和体积
下表中
r 为底面半径,
l 为母线长,
h 为高,
C 为底面周长;特别地,台体
S 与
S′ 分别代表上下底面面积,
r 与
r′ 同理。
棱锥侧面积计算公式中,
a 代表底面边长,
h′ 为斜高。棱台侧面积计算公式中,
C′′,C′ 分别代表上下底面周长,
h′′ 代表斜高。
| 几何体 | 表面积 | 体积 | 侧面积 |
|---|
| 棱柱 | 围成它们的各个面面积之和 | V=Sh | S直棱柱侧=Ch |
| 棱锥 | 围成它们的各个面面积之和 | V=31Sh | S正 n 棱锥侧=21nah′ |
| 棱台 | 围成它们的各个面面积之和 | V=31h(S′+S′S+S) | S正棱台侧=21(C′′+C′)h′′ |
| 圆柱 | S=2πr(r+l) | V=Sh=πr2h | S圆柱侧=2πrl |
| 圆锥 | S=πr(r+l) | V=31Sh=31πr2h | S圆锥侧=πrl |
| 圆台 | S=π(r′2+r2+r′l+rl) | V=31h(S′+S′S+S)=31πh(r′2+r′r+r2) | S圆台侧=π(r+r′)l |
| 球 | S=4πr2 | V=34πr3 | / |
| O 为外心 | O 为内心 | O 为垂心 |
|---|
| 1.PA=PB=PC2.PA,PB,PC 与平面 ABC 所成角相等 | 1.P 到 ΔABC 各边距离相等 2. 三侧面与底面所成二面角相等 | 1.PA⊥PB,PB⊥PC,PA⊥PC2.PA⊥BC,PB⊥AC,PC⊥AB( 三组对棱互相垂直 ) |
球与几何体的外接、内切问题
| 几何体 | 外接球半径 R | 外接球球心 | 内切球半径 r |
|---|
| 长方体 | 2R=a2+b2+c2 | 体对角线的中点 | |
| 正方体 | R=23a | 体对角线的中点 | r=2a 与正方体各棱相切的球 叫做棱切球,半径 22a |
| 直棱柱 / 圆柱 | R2=(2h)2+r2r 为底面外接圆半径 可利用正弦定理求 | 上下底面中心连线的中点 | |
| 侧棱与底面 垂直的锥体 | R2=(2h)2+r2r 为底面外接圆半径 可利用正弦定理求 | 过底面外接圆圆心 且垂直于底面的直线 与垂直于底面的侧棱 的中垂面的交点 | |
| 正棱锥 / 圆锥 | R2=(R−h)2+r2⟹R=2hh2+r2r 为底面外接圆半径 可利用正弦定理求 | 正棱锥 / 圆锥顶点与 底面外心连线 / 延长线上 | |
| 正四面体 高 36a 体积 122a3 | R=46aa 为其棱长 也可用长方体的公式 | | r=126aa 为其棱长 |
空间点、直线、平面之间的关系
- 平面的表示:用横向 / 竖向的平行四边形表示,书写方法:平面 α,β,γ… 或 平面 ABCD,平面 AC,BD。
四个基本事实与三个推论
空间点、直线、平面之间的位置关系
直线与直线⎩⎨⎧共面直线{相交直线:在同一平面内,有且只有一个公共点平行直线:在同一平面内,没有公共点异面直线:不同在任何一个平面内,没有公共点
直线与平面⎩⎨⎧直线在平面内 有无数个公共点直线与平面相交直线与平面平行有且只有一个公共点没有公共点}直线在平面外
直线 a 与平面 α 相交于点 A,记作a⋂α=A 直线 a 与平面 α 平行,记作 a//α
平面与平面{两个平面平行两个平面相交没有公共点有一条公共直线
平面 α 与平面 β 平行,记作 α//β
证明共面、共线、共点
- 证明点、线共面:证明直线平行 / 相交;确定一个辅助平面;反证法。
- 证明三点共线:先找 2 个平面,证明这 3 点都是 2 个平面公共点 / 其中 2 点确定 1 条直线,证另一点也在直线上。
- 证明三线共点:先证明两条直线交于一点,再证明第三条直线经过这个点或交点在第三条直线上。
注意梯形两腰必交于一点;在空间中,不能用两组对边分别相等证明平行四边形。
例题:已知正方体
ABCD−A1B1C1D1,
M,N 为棱
A1B1,B1C1 中点,求证:
(1) 直线
AM,CN 共面;
(2) 直线
D1B 和
CC1 是异面直线。
pf:(1)AA1∥CC1,AA1=CC1⟹ 四边形
ACC1A1 是平行四边形。
AC∥A1C1∥MN⟹ 直线
AM,CN 共面。
(2) 反证法,假设四点共面于
α,则
B,C,C1 可以确定一个平面
BC1,这两个平面重合,又因为
D1B⊂ 平面
BC1,所以
D1∈ 平面
BC1,与
D1∈/ 平面
BC1 矛盾,故原假设错误。
空间直线、平面的平行
-
等角定理:如果空间中两个角的两条边分别对应平行,那么两个角相等或互补。
-
直线与平面平行的判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
用符号表示:
a⊂α,b⊂α,a//b⟹a//α
-
直线与平面平行的性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行。
用符号表示:
a//α,α⋂β=b,a⊂β⟹a//b
-
平面与平面平行的判定定理:如果一个平面内的 两条相交直线 与另一个平面平行,那么这两个平面平行。
用符号表示:
a⊂β,b⊂β,a⋂b=P,a//α,b//α⟹α//β
-
平面与平面平行的性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行。
用符号表示:
α//β,α⋂γ=a,β⋂γ=b⟹a//b
可简记为:线线平行
线面平行
⟹ 面面平行
⟹ 线线平行,恰好形成一个循环。
空间直线、平面的垂直
-
直线与平面垂直的判定定理:如果一条直线与一个平面内的 两条相交直线 垂直,那么该直线与此平面垂直。
用符号表示:
m⊂α,n⊂α,m⋂n=P,l⊥m,l⊥n⟹l⊥α
-
直线与平面垂直的性质定理:垂直于同一个平面的两直线平行。
-
平面与平面垂直的判定定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直。
用符号表示:
a⊂α,a⊥β⟹α⊥β
-
平面与平面垂直的性质定理:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直。
空间直线、平面的平行
-
三棱锥
P−ABC 中,
D,E 分别是
PB,BC 中点,点
F 在线段
AC 上,且满足
AD// 平面
PEF,则
FCAF= ?解析:连接
CD,交
PE 于点
G,连接
FG,如图所示。
AD// 平面
PEF, 平面
PEF ∩ 平面
ADC=FG⟹AD//FG
D,E 分别是
PB,BC 中点
⟹G 是
ΔPBC 重心,
FCAF=GCDG=21。
-
长方体
ABCD−A1B1C1D1,AB=BC,E 是
AB 上靠近
B 的三等分点,
F 是
A1D1 中点,
O 为直线
DB1 与平面
EFC 交点,
OB1DO= ?解析:连接
BD,B1D1,BD∩CE=M,
设平面
CEF 与平面
A1B1C1D1 的交线交
C1D1,B1D1,A1B1 分别于点
P,N,Q,如图所示。
CE//PQ⟹∠PFD1=∠BCE⟹RtΔPFD1∽RtΔECB,FD1PD1=BCEB=31
QA1=PD1=31FD1=61A1B1⟹ND1B1N=PD1B1Q=7
MBDM=EBDC=3⟹DM=43BD⟹OB1DO=NB1DM=76
-
四棱锥
P−ABCD 的底面是边长为
1 的正方形,
E 是
PD 上一点满足
PE=3ED,
若
PF=λPC 且
BF// 平面
AEC,则
λ= ?
解析:连接
BD 交
AC 于点
O,连接
OE,在
PD 上取一点
G 使得
GE=ED。
在
ΔBGD 中
EO 为其中位线
⟹BG// 平面
AEC⟹ 平面
BFG // 平面
AEC。
FCPF=GEPG=2,λ=32
-
在长方体
ABCD−A1B1C1D1 中,
AD=DD1=1,AB=3,E,F,G 分别是
AB,BC,C1D1 的中点,点
P 在平面
ABCD 内,若直线
D1P // 平面
EFG,则点
D1 与满足题意的点
P 构成的平面截长方体所得的截面的面积为 ?
解析:
只需证明点
D1 与满足题意的点
P 构成的平面
D1AC 平行于平面
EFG 即可,答案即为
SΔD1AC=27。
-
如图,三棱柱
ABC−A1B1C1 中,
D 是
B1C1 中点,
E 是
A1C1 上一点满足
A1B// 平面
B1DE,
EC1A1E= ?解析:连接
BC1 交
B1D 于
F,易证
ΔA1BC1∽ΔEFC1,EC1A1E=FC1BF=B1CBD=21。
空间直线、平面的垂直
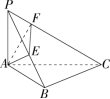
-
如图,
P 是
ΔABC 所在平面外一点,
PA⊥ 平面
ABC,∠ABC=90°,AE⊥PB 于
E,AF⊥PC 于
F. 求证:
(1) BC⊥ 平面
PAB (2) AE⊥ 平面
PBC (3) PC⊥ 平面
AEF解析:
(1) ∠ABC=90°⟹BC⊥AB PA⊥ 平面
ABC⟹BC⊥PA (2) BC⊥ 平面
PAB⟹AE⊥BC (3) AE⊥ 平面
PBC⟹PC⊥AE
定理 & 二级结论
-
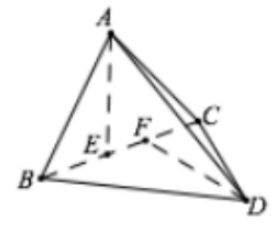
空间第二余弦定理:空间中两直线
AB,CD 的夹角
θ 满足
cosθ=2AB⋅CD∣AD2+BC2−AC2−BD2∣证明:
AC⋅BD=AC⋅(AD−AB)=∣AC∣∣AD∣cos∠CAD−∣AC∣∣AB∣cos∠CAB=AC⋅AD⋅2AC⋅ADAC2+AD2−CD2−AC⋅AB⋅2AC⋅ABAC2+AB2−BC2=2AD2+CB2−AB2−CD2
-
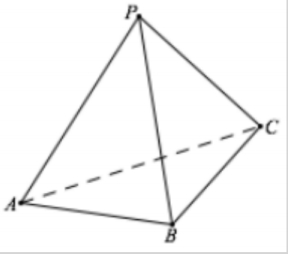
三面角公式求二面角:已知
∠APB=θ1,∠BPC=θ2,∠APC=θ3,则二面角
A−PB−C 的余弦值为
cosθ=sinθ1sinθ2cosθ3−cosθ1cosθ2=sin∠APB⋅sin∠BPCcos∠APC−cos∠APB⋅cos∠BPC
注意三个角度在公式中分布特点,
θ3 是二面角
A−PB−C 的对角,而
θ1,θ2 就是二面角
A−PB−C 的两个邻角
-
三正弦定理:二面角
M−AB−N 的度数为
α,平面
M 上有一射线
AC 与
AB 所成角为
β,与平面
N 所成角为
γ,则
sinγ=sinαsinβ。
-
三余弦定理 / 最小角定理:设
A 为平面
α 上一点,过点
A 的斜线
AO 在平面
α 上的射影为
AB,
AC 为平面
α 内的一条直线,那么有
cos∠OAC=cos∠BAC×cos∠OAB。
证明:
cos∠OAC=AOAC cos∠BAC=ABAC cos∠OAB=AOAB即斜线与射影所成的角是斜线与平面内的任何直线所成的角中最小的角。
-
异面直线段
AB=a,CD=b,它们之间的距离为
d,夹角为
θ,则
VA−BCD=61abdsinθ。
-
面积余弦定理:
ΔABC 在平面
α 内的射影为
ΔABO,记
ΔABC 所在平面与
α 所称的锐二面角为
θ,则
SΔABO=cosθSΔABC。
翻折问题
- 不在同一平面的两点路径问题的翻折只能以折点所在直线翻折。
例:长方体
ABCD−A1B1C1D1 中,
AB=1,AD=2,AA1=3,P 是线段
B1C 上一动点,求
AP+PD1 的最小值 ?
画出直观图后,应将平面
AB1C 和平面
B1CD1 翻折到同一平面上,显然
AB1D1C 是平行四边形。
根据平行四边形中对角线平分和
= 四条边平方和可得
(AP+PD1)min=AD1=17。
例:直三棱柱
ABC−A1B1C1 中,
E,F 分别为
AA1,C1B1 的中点,沿棱柱的表面从
E 到
F 两点的最短路径的长度是 ?
分三类讨论:
- 沿 BB1 展开,算得 EF=222。
- 沿 A1C1 展开,算得 EF=232。
- 沿 A1B1 展开,算得 EF=27+2。
于是
EFmin=232。
截面问题
-
求过圆锥顶点的截面面积最大值:记轴截面顶角为
θ,
sinθ=lr {θ>2π,Smax=21l2sinθ⟹21l2θ≤2π,Smax= 轴截面面积
-
正方体棱长为
1,每条棱所在直线与平面
α 所称角相等,则
α 截此正方体所得截面面积最大值 ?
注意正方体截面可以是
3,4,5,6 边形,最大面积是
433。
例题:在棱长为
2 的正方体
ABCD−A1B1C1D1 中,
E 为棱
AA1 中点,点
F 在
A1B1 上且满足
A1F=λA1B1,以下正确的有(
ACD )
A. 当
λ=0 时,
AC1⊥ 平面
BDF。
B. ∀λ∈[0,1],VF−BDE 不变。
C. ∃λ∈[0,1],直线
AC 与平面
BDF 所成角为
3π。
D. 当
λ=32 时,平面
BDF 截正方体外接球所得截面面积为
1956π。
首先把平面补全为
BDGF,其中
G 为棱
A1D1 上靠近
D1 的三等分点。
连接
A1C1 与
GF,B1D1 分别交于点
P,Q,连接
AC 与
BD 交于点
E,连接
PE。
显然正方体外接球球心
O 为线段
QE 中点,记截面所在圆的圆心为
O1,则
OO1⊥ 平面
BDF。
因为
P,E 均为对角线上的点,所以
O1 在线段
PE 上。
于是
RtΔPQE∼RtΔOO1E,可算得
PQ=32,PE=338,OO1=191。
正方体外接球半径
R=3,截面圆半径
r=R2−OO12=192266,S=πr2=1956π。
空间向量
基本运算同平面向量。
- OP=xOA+yOB+zOC 且 x+y+z=1,A,B,C 不共线,O⊂ 平面 ABC⟹A,P,B,C 四点共面。
证明:
AP=mAC+nAB=OP−OA=m(OC−OA)+n(OB−OA)=(1−m−n)OA+nOB+mOC
-
若
ΔABC 重心为
G,
O 为
ΔABC 平面外一点,则
OG=31(OA+OB+OC)。
-
法向量:垂直于平面
α 的向量,有无数多个;怎么求:设法向量为
(x,y,z),求出平面内两个向量的坐标表示,点乘列方程组求。
-
速求法向量:已知平面
α 上的两个向量
a=(x1,y1,z1),b=(x2,y2,z2),则平面的一个法向量为
(y1y2z1z2,z1z2x1x2,x1x2y1y2)=(y1z2−y2z1,z1x2−z2x1,x1y2−x2y1)。
相当于求向量叉乘。
-
对称问题
(a,b,c) 关于什么对称,什么就不变。
| 原点 O | x 轴 | y 轴 | z 轴 | Oxy 平面 | Oyz 平面 | Oxz 平面 |
|---|
| (−a,−b,−c) | (a,−b,−c) | (−a,b,−c) | (−a,−b,c) | (a,b,−c) | (−a,b,c) | (a,−b,c) |
平面方程
-
过
P(x0,y0,z0) 且法向量
m=(A,B,C) 的平面方程为
A(x−x0)+B(y−y0)+C(z−z0)=0。
-
过
P(x0,y0,z0) 且方向向量
n=(u,v,w) 的直线
l 的方程为
ux−x0=vy−y0=wz−z0 (uvw=0)。
用空间向量研究距离、夹角问题
-
点线距 —— 求点
A 到直线
BC 的距离。
a=BA,u=∣BC∣BC,d=a2−(a⋅u)2
-
点面距 / 线面距 / 面面距 —— 求点
A 到平面
BCD 的距离。
- 等体积法,VA−BCD=VB−ACD=VC−ABD=VD−ABC
- 求平面 BCD 的法向量 n,d=∣n∣∣BA⋅n∣
- A(x0,y0,z0),平面的解析式 Ax+By+Cz+D=0,d=A2+B2+C2∣Ax0+By0+Cz0+D∣
-
线线角 —— 求
AB,CD 夹角
θ
- 求出它们的方向向量 u,v,则 cosθ=∣AB∣∣CD∣AB⋅CD=∣u∣∣v∣∣u⋅v∣
- 空间第二余弦定理 cosθ=2AB⋅CD∣AD2+BC2−AC2−BD2∣
-
线面角 ——
sinθ=∣u∣∣n∣∣u⋅n∣ ,较难做的题目亦可用等体积法。
-
二面角 ——
cosθ=∣n1∣∣n2∣∣n1⋅n2∣
| 两直线所成角 | 异面直线所成角 | 线面角 | 平面与平面的夹角 | 二面角 | 向量夹角 | 倾斜角 |
|---|
| [0,2π] | (0,2π] | [0,2π] | [0,2π] | [0,π] | [0,π] | [0,π) |
向量叉乘
- 若 a=axi+ayj+azk,b=bxi+byj+bzk,则 c=a×b=iaxbxjaybykazbz
叉乘的结果是向量,该向量的模值与
a,b 构成的平行四边形面积相等,即
∣a×b∣=∣a∣∣b∣∣sinθ∣=x1y2−x2y1。
该向量的方向垂直于
a,b 构成的平面,用右手螺旋性质确定。
运算特性:
⎩⎨⎧a×b=−b×aa×a=0a×(b+c)=a×b+a×c(a×b)×c=(a⋅c)b−(b⋅c)a  解析:连接 ,交 于点 ,连接 ,如图所示。
解析:连接 ,交 于点 ,连接 ,如图所示。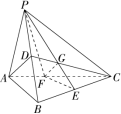 平面 , 平面 平面分别是 中点 是 重心,。
平面 , 平面 平面分别是 中点 是 重心,。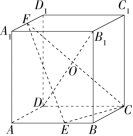 解析:连接 , 设平面 与平面 的交线交 分别于点 ,如图所示。
解析:连接 , 设平面 与平面 的交线交 分别于点 ,如图所示。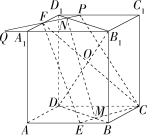
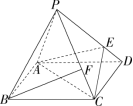 解析:连接 交 于点 ,连接 ,在 上取一点 使得 。
解析:连接 交 于点 ,连接 ,在 上取一点 使得 。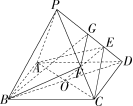 在 中 为其中位线 平面 平面 平面 。
在 中 为其中位线 平面 平面 平面 。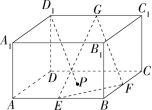 解析:
解析: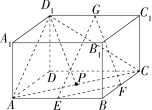 只需证明点 与满足题意的点 构成的平面 平行于平面 即可,答案即为 。
只需证明点 与满足题意的点 构成的平面 平行于平面 即可,答案即为 。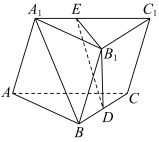 解析:连接 交 于 ,易证 。
解析:连接 交 于 ,易证 。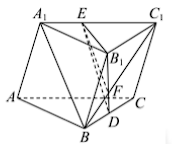
 解析: 平面 平面 平面
解析: 平面 平面 平面