平面几何
Menelaus 梅涅劳斯定理
FBAFDCBDEACE=1
第一角元形式:
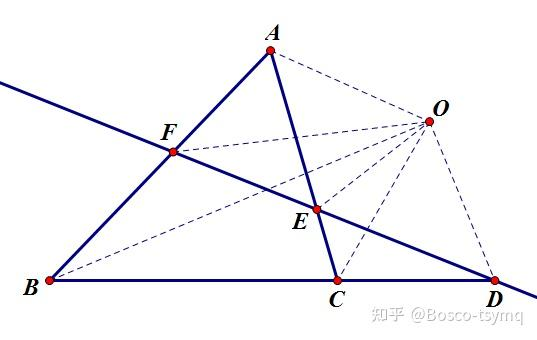
sin∠FCBsin∠ACFsin∠DACsin∠BADsin∠EBAsin∠CBE=1第二角元形式:
sin∠FOBsin∠AOFsin∠DOCsin∠BODsin∠EOAsin∠COE=1Ceva 塞瓦定理
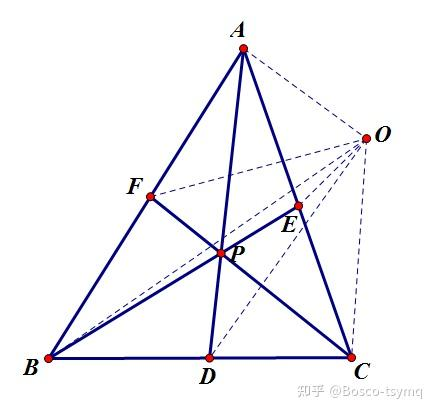
FBAFDCBDEACE=1
第一角元形式:
sin∠FCBsin∠ACFsin∠DACsin∠BADsin∠EBAsin∠CBE=1第二角元形式:
sin∠FOBsin∠AOFsin∠DOCsin∠BODsin∠EOAsin∠COE=1Stewart 定理
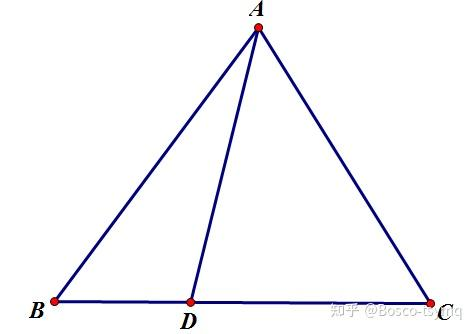
AD2=BCAC2⋅BD+AB2⋅DC−BD⋅DC
中线长公式:
ma2=21AB2+21AC2−41BC2角平分线长公式:
ta=AB⋅AC−BD⋅DC=AB+AC2AB⋅AC⋅p⋅(p−BC),p=2AB+BC+CA调和点列
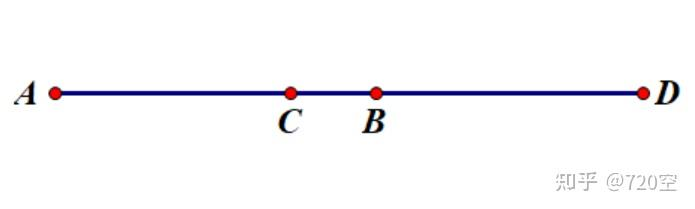
定义:若
CBAC=DBAD,则称
(A,B,C,D) 为调和点列,
C,D 调和分割线段
A,B。
- AC1+AD1=AB2,即 AB 的长度是 AC 和 AD 长度的调和平均值。
- AB⋅CD=2AD⋅BC=2AC⋅DB
- CA⋅CB=CM⋅CD,DA⋅DB=DM⋅DC
- MA2=MB2=MC⋅MD
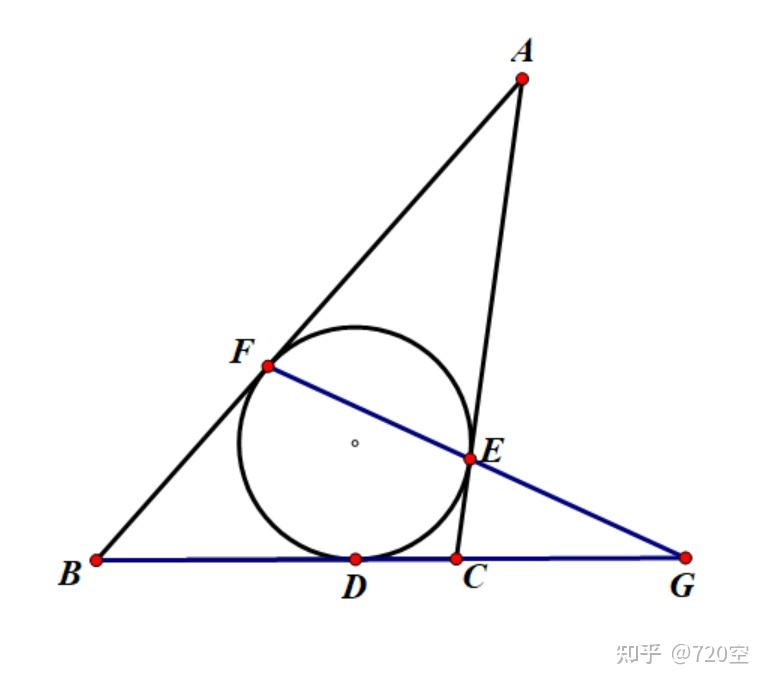
内切圆和调和点列
由梅涅劳斯定理得
FBAFGCBGEACE=1,又因为
AF=AE,BF=BD,CE=CD,
得
CDBD=CGBG⟹(B,D,C,G) 为调和点列。
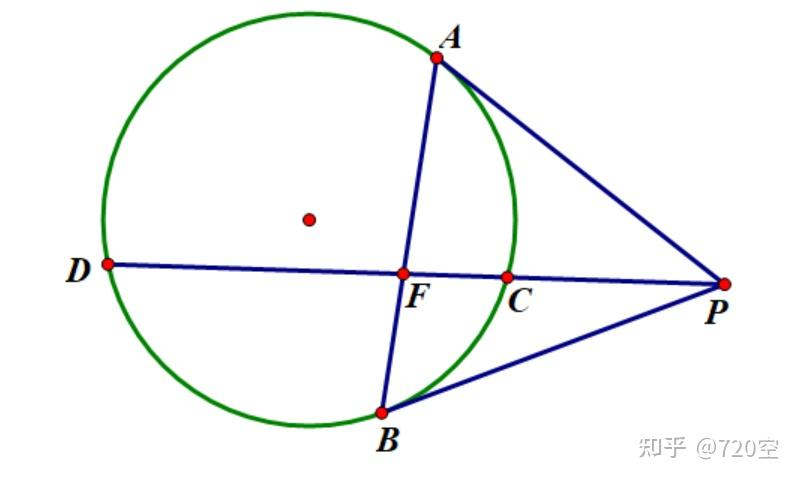
极线和调和点列
PA,PB 为两条切线,
P 是极点,
AB 是极线,则
DPCP=DFCF,(P,C,F,D) 是调和点列。
线性规划
例题 1
⎩⎨⎧5x−11y≥−222x+3y≥92x≤11
z=10x+10y,maxz= ?
基本概念
- 约束条件:变量 x,y,… 满足的一组条件,上述二元一次不等式组就是对 x,y 的约束条件。
- 线性约束条件:由变量 x,y,… 的一次不等式 / 方程组成的不等式组就称为线性约束条件,如上述二元一次不等式。
- 目标函数:欲求最大值或最小值所涉及的变量 x,y,… 的解析式,如上述 z。
- 线性目标函数:目标函数关于变量 x,y,… 的一次解析式,如上述 z。
- 线性规划问题:在线性约束条件下求线性目标函数的问题。
- 可行解:满足线性约束条件的解 (x,y)。
- 可行域:由所有可行解组成的集合。
- 最优解:使目标函数取得 max 或 min 的可行解。
解法
-
画图,数形结合。
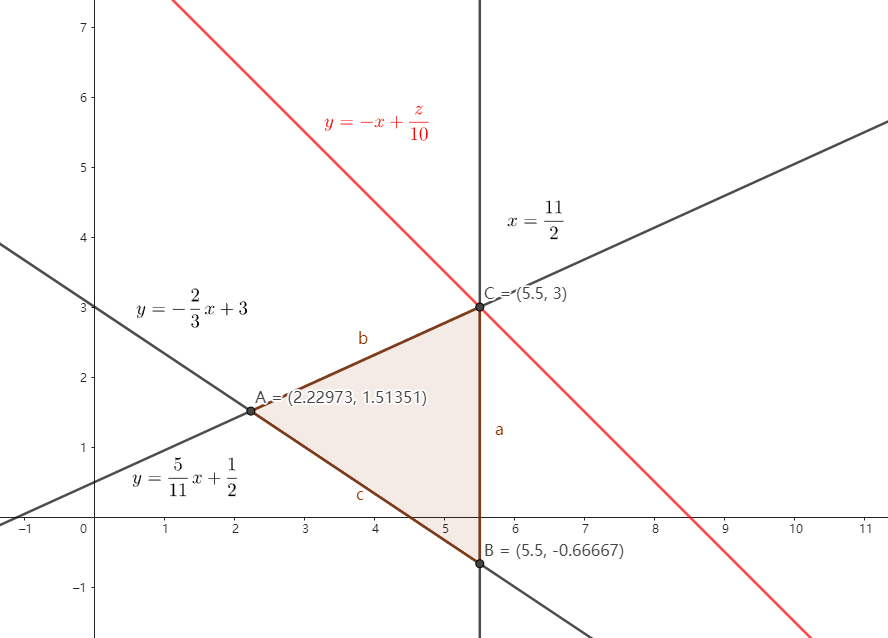
⎩⎨⎧5x−11y≥−222x+3y≥92x≤11⟹y≤115x+21⟹y≥−32x+3⟹x≤211⟹⟹⟹y=115x+21 图像的下边y=−32x+3 图像的上边x=211 图像的左边
在平面直角坐标系上画出对应的平面区域 ( 可行域 ),再把目标函数
z=ax+by 变形为
y=−bax+bz,
所以求
z 的最值可看成是求直线
y=−bax+bz 在
y 轴上截距的最值。以这题为例,
z=10x+10y⟹y=−x+10z 容易证明,当
z=85 时
y 轴上截距取最值,所以
maxz=85.
-
仔细观察,可以发现最优解非常容易出现在可行域构成的多面体的顶点处。
例题 2
⎩⎨⎧y≥xx+y≤2x≥a
(2x+y)max=4(2x+y)min, a= ?
-
求
(2x+y)min:
xmin=a⟹ymin=a⟹(2x+y)min=3a
-
求
(2x+y)max:
{x−y≤0x+y≤2Add x≤1⟹y≤1⟹(2x+y)max=3
-
3=4×3a⟹a=41
例题 3( 2024 九省联考 T14 )
{0<a<b<c<1b≥2a or a+b≤1
max{b−a,c−b,1−c} 的最小值
= ?
- 注意到 c 的约束条件是最少的,首先考虑消去它,得到
max{b−a,c−b,1−c}≥max{b−a,21−b}
当且仅当
c=21+b 取等,消去
c 后把
a 看作
x,把
b 看作
y 得:
⎩⎨⎧0<xx<yy<1y≥2x or x+y≤1
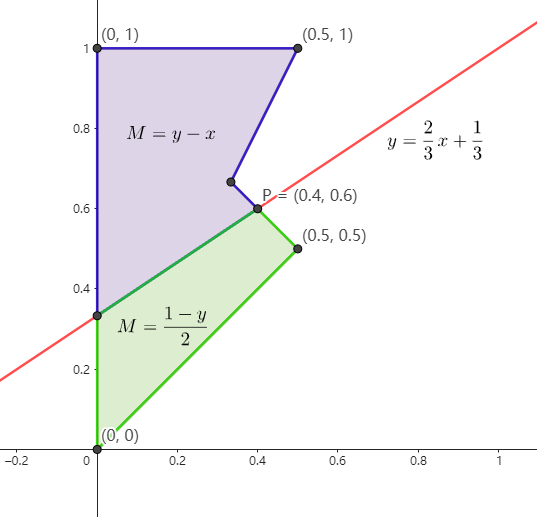
- 作出可行域:and 连接的区域之间取交,or 连接的区域之间取并。阴影部分即为可行域。
图中
y≥2x x+y≤1 两条解析式用红色标出。
- 回到题目,要求 M=max{y−x,21−y},我们需要知道何时 M=y−x,何时 M=21−y
直接列方程
y−x=21−y 可以得到
y=32x+31,在图中作出这条直线,得到:
- 因为最终要求的是 M 的最小值,所以对蓝色区域而言,y 尽量小,x 尽量大,根据例题 1 的经验,这样的极值点通常出现在多边形的顶点处,经过比较后 P 点是极值点,此时 M=0.2。对绿色区域而言,只需满足 y 尽量大,显然,P 点也是极值点。
- 综上所述,max{b−a,c−b,1−c} 的最小值 =51。
数论
因为这里是数学笔记,不是 OI 笔记,因此只有一些简要的定理。
质数
-
定义:一个正整数无法被除了
1 和它自身之外的任何自然数整除,则成为质数,否则为合数。
-
数量:对于一个足够大的整数
N,不超过
N 的质数有
π(x)≈lnNN 个,所以第
n 个质数约为
nlnn。
-
判定:试除法,若
N 为合数,则存在一个能整除
N 的数
T 且
2≤T≤N。
-
算数基本定理:
N=p1c1p2c2…pncn,
N 的正约数个数
=i=1∏n(ci+1),
N 的所有正约数的和
=i=1∏n(j=0∑ci(pi)j)。
一个正整数
N 的约数个数上界为
2N,
1 ~
N 每个数的约数个数的总和大约为
NlogN。
因数
整除
若
b 能整除
a,则记为
a∣b,如
2∣12。若
b 不能整除
a,则记为
a∤b,如
5∤12。
若
a∤b,则
b÷a 存在余数
r 且
0<r<a,记
r=a mod b。例如,
3 mod 2=1。
整除具有以下性质:
- 若 a∣b 且 a∣c,则 ∀x,y,有 a∣xb+yc。
- 若 a∣b 且 b∣c,则 a∣c。
- 若 a∣b 且 b∣a,则 a=±b。
- 设 m=0,则 a∣b,当且仅当 ma∣mb。
最大公因数与最小公倍数
设
a,b 是两个不为
0 的整数,能使
d∣a 和
d∣b 成立的最大整数
d,称为
a,b 的最大公因数,记作
gcd(a,b)。
设
a,b 是两个不为
0 的整数,能使
a∣d 和
b∣d 成立的最小整数
d,称为
a,b 的最小公倍数,记作
lcm(a,b)。
- ∀a,b∈N, gcd(a,b)⋅lcm(a,b)=ab
证明:设
d=gcd(a,b),a0=da,b0=db。根据最大公因数的定义,有
gcd(a0,b0)=1。
再根据最小公倍数的定义,有
lcm(a,b)=a0⋅b0。
于是
lcm(a,b)=lcm(a0⋅d,b0⋅d)=lcm(a0,b0)⋅d=a0⋅b0⋅d=da⋅b,原命题得证。
- 九章算术 更相减损术: gcd(a,b)=gcd(b,a−b)=gcd(a,a−b),gcd(2a,2b)=2gcd(a,b)。
证明:
d∣a,d∣b⟹d∣(a−b)。
- 欧几里得算法:∀a,b∈N,b=0,gcd(a,b)=gcd(b,a mod b)。
证明:分类讨论。
- 若 a<b,则有 gcd(b,a mod b)=gcd(b,a)=gcd(a,b)。
- 若 a≥b,不妨设 a=q⋅b+r (0≤r<b)。显然 r=a mod b。对于 a,b 的任意公因数 d, 因为 d∣a,d∣q⋅b,故 d∣(a−q⋅b),即 d∣r。因此 d 也是 b,r 的公因数,反之亦成立。 故 a,b 的公因数集合与 b,a mod b 的公因数集合相同。于是它们的最大公因数也相等。
欧拉函数
1 ~
N 中与
N 互质的数的个数被称为欧拉函数,记为
φ(N)。用数学符号表示即为
φ(N)=i=1∑N[gcd(i,N)=1]。
若
N=p1c1p2c2…pncn,则
φ(N)=N×p1p1−1×p2p2−1×⋯×pnpn−1=N⋅质数p∣N∏(1−p1)证明:设
p,q 为
N 的不同质因子,
1 ~
N 中
p 的倍数有
pN 个,
q 的倍数有
qN 个。若把
pN+qN 个数去掉,则
pqN 被计算了
2 次( 容斥原理 )。因此,
1 ~
N 中不与
N 含有相同质因子的
p 或
q 数量为
N−pN−qN+pqN=N(1−p1)(1−q1),对
N 的全部质因子继续容斥即可得到公式。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|
| φ(n) | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 | 10 | 4 | 12 | 6 | 8 |
欧拉函数的性质:
- ∀n>1,1 ~ n 中与 n 互质的数的和为 2n×φ(n)。
- 若 a,b 互质,则 φ(ab)=φ(a)φ(b)。
- 设 p 为质数,φ(p)=p−1。
- 设 p 为质数,k∈N∗,φ(pk)=pk−1×(p−1)=pk−pk−1。
- 设 p 为质数,若 p∣n 且 p2∣n,则 φ(n)=φ(pn)×p。
- 设 p 为质数,若 p∣n 但 p2∤n,则 φ(n)=φ(pn)×(p−1)。
- 若 n 为奇数,则 φ(2n)=φ(n)。
- ∀n≥3, n∈N∗, 2∣φ(n)。
- 欧拉反演:d∣n∑φ(d)=n。
证明:
- 因为 gcd(n,x)=gcd(n,n−x),所以与 n 不互质的数 x,n−x 成对出现,平均值为 2n。 因此与 n 互质的数的平均值也是 2n,进而得到性质 1。
- 根据欧拉函数的计算式可直接获得性质 2。
- 根据欧拉函数的定义可直接获得性质 3。
- 从 1 ~ pk 中的所有数,除了 pk−1 个 p 的倍数外都与 pk 互素。
- 若 p∣n 且 p2∣n,则 n,pn 包含相同的质因子,只是 p 的指数不同。 按照欧拉函数的计算公式,φ(pn)φ(n)=pnn=p,得到性质 5。
- 若 p∣n 且 p2∣n,则 n,pn 互质。因为 φ(n)=φ(pn)φ(p),而 φ(p)=p−1,得到性质 6。
- ∀m<2n,m∈N∗,若 2∣m,则 gcd(m,2n)=1,也就是对欧拉函数的值没有贡献;若 2∤m,则 gcd(m,2n)=1,欧拉函数的值也就与 2n 中的偶质因子无关。
- n≥3 时,与 n 互质的数不可能为 2n⟹∀x<n,gcd(x,n)=gcd(n−x,n),也就是存在一一对应关系。
- 设 f(n)=d∣n∑φ(d),利用 φ 是积性函数,得到:若 n,m 互质,则 f(nm)=d∣nm∑φ(d)=d∣n∑φ(d)⋅d∣m∑φ(d)=f(n)f(m),即 f(n) 是积性函数。 对于单个质因子有:f(pm)=d∣pm∑φ(d)=i=0∑mφ(pi)=φ(1)+φ(p)+φ(p2)+φ(p3)+⋯+φ(pm)=1+(p−1)+(p−1)p+(p−1)p2+⋯+(p−1)pm−1=1+(p−1)+(p2−p)+(p3−p2)+⋯+(pm−pm−1)=pm 所以 f(n)=i=1∏mf(pici)=i=1∏mpici=n
积性函数与完全积性函数
若函数
f(x) 满足
f(1)=1 且
∀x,y∈N∗,gcd(x,y)=1 都有
f(xy)=f(x)f(y),则
f(x) 是积性函数。
若函数
f(x) 满足
f(1)=1 且
∀x,y∈N∗ 都有
f(xy)=f(x)f(y),则
f(x) 是完全积性函数。
性质:
-
若
f(x) 和
g(x) 均为积性函数,则以下函数也为积性函数:
h(x)h(x)h(x)h(x)=f(xp)=fp(x)=f(x)g(x)=d∣x∑f(d)g(dx)
-
设
x=∏pici,
若
f(x) 为积性函数,则
f(x)=∏f(pici)。
若
f(x) 为完全积性函数,则
f(x)=∏fci(pi)。
例子:
积性函数:
φ(n),σk(n)=d∣n∑dk,σ0(n) 通常简记为
d(n) 或
τ(n),
σ1(n) 通常简记为
σ(n)。
完全积性函数:
ε(n)=[n=1],idk(n)=nk,id1(n) 通常简记为
id(n),f(n)=1。
同余
费马小定理与欧拉定理
若整数
a 和整数
b 除以正整数
m 的余数相等,则称
a,b 模
m 同余,记为
a≡b (mod m)。
并且注意到
k mod i=k−⌊ik⌋⋅i,且同余满足同加性、同乘性、同幂性,但不满足同除性。
对于
∀a∈[0,m−1],集合
{a+km (k∈Z)} 的所有数模
m 同余,余数都是
a。该集合称为一个模
m 的同余类,简记为
a。
模
m 的同余类一共有
m 个,分别为
0,1,2,…,m−1。它们构成
m 的完全剩余系。
1 ~
m 中与
m 互质的数代表的同余类共有
φ(m) 个,它们构成
m 的简化剩余系。
例如,模
10 的简化剩余系为
{1,3,7,9}。
若从某个非空数集中任选两个元素( 同一元素可重复选出 ),选出的这两个元素通过某种( 或几种 )运算后的得数仍是该数集中的元素,那么,就说该集合对于这种( 或几种 )运算是封闭的。
例如若一个集合中的元素,如果能够做到做加法运算的结果还在这个集合中,就说这个集合对加法运算封闭。
例如
N 对加法、乘法运算是封闭的;
Z 对加、减、乘法运算是封闭的;
Q,C 对四则运算是封闭的。
简化剩余系关于模
m 乘法封闭。这是因为若
a,b (1≤a,b≤m) 与
m 互质,则
ab 也与
m 互质。
由余数的定义得
ab mod m 也与
m 互质,即
ab mod m 也属于
m 的简化剩余系。
- 费马小定理:若 p 是质数,则对于任意整数 a,有 ap≡a (mod p)。
- 欧拉定理:若正整数 a,n 互质,则 aφ(n)≡1 (mod n)。
证明:设
n 的简化剩余系为
{a1,a2,…,aφ(n)}。
∀ai,aj,若
a⋅ai≡a⋅aj (mod n),则
a⋅(ai−aj)≡0 因为
a,n 互质,所以
ai≡aj。故当
ai=aj 时,
aai,aaj 也代表不同的同余类。
又因为简化剩余系关于模
m 乘法封闭,故
aa1 也在简化剩余系集合中。因此,集合
{a1,a2,…,aφ(n)} 与集合
{aa1,aa2,…,aaφ(n)} 都能表示
n 的简化剩余系。综上所述:
aφ(n)a1a2…aφ(n)≡(aa1)(aa2)…(aaφ(n))≡a1a2…aφ(n) (mod n)
因此
aφ(n)≡1 (mod n)。当
p 为质数时,满足
φ(p)=p−1,两边同乘
a 即可得到费马小定理。
另外,当
a 是
p 的倍数,费马小定理显然成立。
- 欧拉定理的推论:若正整数 a,n 互质,则对于任意正整数 b,有 ab≡ab mod φ(n) (mod n)
证明:设
b=q⋅φ(n)+r,其中
0≤r<φ(n),即
r=b mod φ(n)。于是有:
ab≡aq⋅φ(n)+r≡(aφ(n))q⋅ar≡1q⋅ar≡ar≡ab mod φ(n) (mod n)
证毕。面对
a+b,a−b,a⋅b 这样的算式,可以在计算前先把
a,b 对
p 取模。面对
ab 这样的乘方算式,可以先把底数对
p 取模、指数对
φ(p) 取模,再计算乘方。
即
ab≡(a mod p)b mod φ(p) (mod p)
-
扩展欧拉定理
ab≡⎩⎨⎧ab mod φ(m)abab mod φ(m)+φ(m)if gcd(a,m)=1if gcd(a,m)=1,b<φ(m)if gcd(a,m)=1,b≥φ(m) (mod m)
证明十分显然,略。
- 若正整数 a,n 互质,则满足 ax≡1 (mod n) 的最小正整数 x0 是 φ(n) 的约数。
反证法,假设满足
ax≡1 (mod n) 的最小正整数
x0 不能整除
φ(n)。
设
φ(n)=qx0+r (0<r<x0),因为
ax0≡1 (mod n),所以
aqx0≡1 (mod n)。根据欧拉定理
aφ(n)≡1 (mod n),所以
ar≡1 (mod n)。这与
x0 最小矛盾。故假设不成立,原命题成立。
中国剩余定理
设
m1,m2,…,mn 是两两互质的整数,
m=i=1∏nmi,Mi=mim,ti 是线性同余方程
Miti≡1 (mod mi) 的一个解。对于任意的
n 个整数,方程组
⎩⎨⎧x≡a1 (mod m1)x≡a2 (mod m2) ⋮x≡an (mod mn)
有整数解,解为
x=i=1∑naiMiti,通解可以表示为
x+km(k∈Z),最小非负整数解为
x mod m。
证明:因为
Mi=mim 是除了
mi 之外所有模数的倍数,所以
∀k=i,aiMiti≡0 (mod mi),
所以代入
x=i=1∑naiMiti,原方程组成立。
威尔逊定理
- p 为素数 (p−1)!≡−1 (mod p)
证明:
-
充分性
对于
p 不是素数的情况,有
⎩⎨⎧p=1p=4p>4(1−1)!≡0 (mod 1)(4−1)!≡2 (mod 4)分类讨论得出 (p−1)!≡0 (mod p)则
p=k2 且
k>2,用相减法比较
2k 与
p 的大小得
2k<p,于是有
(p−1)!=1×2×⋯×k×⋯×2k×⋯×(p−1)=2nk2=2np
所以
(p−1)!≡0 (mod p) 且
p 为完全平方数。
则
p 可以表示为两个不相等的数
a 和
b 的乘积,设
a<b,则有
p=ab,1<a<b<p(p−1)!=1×2×⋯×a×⋯×b×⋯×(p−1)=a×b×n=np
所以
(p−1)!≡0 (mod p) 且
p 不为完全平方数。
-
必要性
当
p 为素数时,考虑二次剩余式
x2≡1 (mod p),化简得
(x−1)(x+1)≡0 (mod p)于是
x≡1 (mod p) 或
x≡p−1 (mod p)。现在先抛开
1 和
p−1 不管,
∀a∈[2,p−2],必然存在一个和它不相等的逆元
a−1∈[2,p−2],满足
aa−1≡1 (mod p)
所以必然有
2p−3 对数相乘的乘积为
1,即
(p−2)!≡1 (mod p)等式两边同时乘
p−1 就得到威尔逊定理。
例题:
n∈N∗ 且
n≤106,求
Sn。
Sn=k=1∑n⌊3k+7(3k+6)!+1−⌊3k+7(3k+6)!⌋⌋
令
d=3k+7,原式化简为
Sn=k=1∑n⌊d(d−1)!+1−⌊d(d−1)!⌋⌋
由威尔逊定理,当
d 为素数时,
d(d−1)!+1 必然是整数,而
⌊d(d−1)!⌋ 必然比
d(d−1)!+1 小
1,于是有:
{p 为素数p 为合数⌊d(d−1)!+1−⌊d(d−1)!⌋⌋=1⌊d(d−1)!+1−⌊d(d−1)!⌋⌋=0
所以只需统计
[1,3×106+7] 中的素数即可得出答案。
牛顿迭代
对于在
[a,b] 上连续且单调的函数
f(x),牛顿迭代法可用于求解方程
f(x)=0 的近似解。
初始时先从给定的
f(x) 和近似解
x0 开始,
x0 可以是随机数。然后我们可以得到
f(x0)。
接着,画出与
f(x) 切于点
(x0,f(x0)) 的直线
l0,将
l0 与
x 轴的交点横坐标记为
x1,
x1 就是更优的近似解。
重复这个迭代过程,可以得到:
f′(xi)=xi−xi+1f(xi)⟹xi+1=xi−f′(xi)f(xi)
优点:收敛率是平方级别的,这意味着每次迭代后近似解的精确数位会翻倍。
缺点:不能处理重复的根;解可能在拐点附近发散;解可能在局部极小值或最大值附近振荡;当斜率接近于零时,解可能发散或到达不同的根。
拉格朗日插值法
由
n 个点可以唯一确定一个多项式
y=f(x)(不含
log,ax), 当已知这
n 个点的坐标要求
f(k) 有:
f(k)=i=1∑nyi(i=j∏1≤j≤nxi−xjk−xj)
如果已知
f(1),f(2),…,f(n),f(n+1),要求
f(x) 有:
f(x)=i=1∑n+1(−1)n+1−i⋅yi⋅(i−1)!(n+1−i)!(x−i)j=1∏n+1(x−j)