在讨论《警示后人》回复：

thx

在讨论《（二金三银四铜）2026 年米兰科尔蒂纳冬奥会专题讨论帖》回复：

神秘180转身

在讨论《求原题机网址》回复：

@[_Seren_](luogu://user/1794511) [this](https://yuantiji.ac/zh/)

在讨论《关于平面图（再问》回复：

已知若存在13阶最小度为5的平面图，其度数必为12个5度点和1个6度点。

12阶存在最小度为5的平面图（此时为最小阶数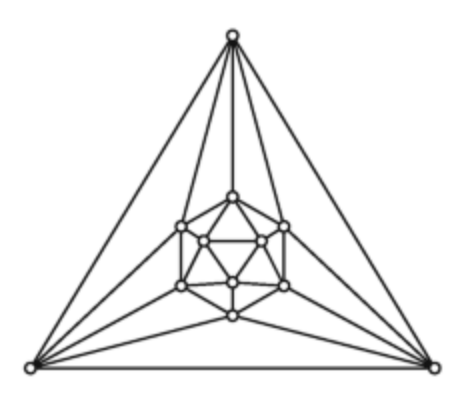）：  如何证明证明13阶不存在最小度为5的平面图？（本来找到了一篇证明过程，但并没有看懂其中第三个定理，仍然一头雾水 :<

在讨论《（二金三银四铜）2026 年米兰科尔蒂纳冬奥会专题讨论帖》回复：

冰壶now

在讨论《求问，关于平面图》回复：

[此贴结](https://math.stackexchange.com/revisions/5d7a054b-0f4b-4399-bfce-e9e031ca732f/view-source)

[前言](https://www.luogu.com.cn/discuss/1248869) 如何证明证明13阶不存在最小度为5的平面图？

在讨论《关于最小度为5的平面图》回复：

=@[zjck2](luogu://user/1347790) em我想想

众所周知，最小度数恰为5的平面图的最小阶数为12（欧拉公式易证，此时为12阶5-正则极大平面图：  但似乎13阶不存在最小度为5的平面图，查询资料也没有找到相关证明，是否有清晰的方法证明13阶不…

在讨论《警示后人（90pts MLE on #4）》回复：

thx

在讨论《de，不知道哪认错了，兄弟们，帮我找一找。》回复：

@[fansimin](luogu://user/2072953) 输出最好也用 ```%.12lf```（```%lf```适配double类型）。

在讨论《求原题》回复：

（暂无内容）

在讨论《（二金三银四铜）2026 年米兰科尔蒂纳冬奥会专题讨论帖》回复：

@[chen_zhe](luogu://user/8457) 孙龙获男子短道速滑1000米银牌

在文章《WC 2026 游记》发表评论：

加油 :>

在讨论《（二金三银四铜）2026 年米兰科尔蒂纳冬奥会专题讨论帖》回复：

蔡雪桐、武绍桐晋级。

在讨论《迷茫中》回复：

3 4

在讨论《平面图与对偶图相关》回复：

@[OIer_Automation](luogu://user/528787) [这篇文章](https://link.springer.com/chapter/10.1007/978-981-96-4745-3_5)后部分有所提及n=12~19的最小度数为5的平面图，但快速构造点数为 $n$ 的满足条件的图感觉难以实…

在讨论《平面图与对偶图相关》回复：

@[OIer_Automation](luogu://user/528787) 我记得有篇文章提到了12阶的构造方法，我找找。

在讨论《求问部分分难度》回复：

@[Eclatara](luogu://user/1123633) 大致如此

在讨论《（二金三银四铜）2026 年米兰科尔蒂纳冬奥会专题讨论帖》回复：

中国队出场了

在讨论《LCOI-R1、LGR-266、LGR-267 作弊名单》回复：

qp，不置顶喵？

在文章《欢迎来到青岛，欢迎来到青岛市城阳第一高级中学。》发表评论：

肚子的在 cyyz 的圆角超过人类水平一万年

在文章《[技巧] 当你「使用影跃」就可以解决你「两年的梦魇」？！》发表评论：

还在五

在讨论《建议评绿+添加标签》回复：

@[jzy_CSPJ_AK](luogu://user/1034698) 发工单

在讨论《社会调查》回复：

done

在文章《再谈概率期望（二）》发表评论：

@clx201022 记得更新喵。

在文章《再谈概率期望（二）》发表评论：

good

在讨论《好题分享×4》回复：

紫衫吧。

在讨论《求可持久化好文》回复：

@[zszl](luogu://user/1328402) 可持久化trie和主席树可以看[这篇](https://www.luogu.me/article/rwvzn9ds)或[这篇](https://www.cnblogs.com/flashhu/p/8297581.html) 可持久化并查集看[这篇](https…