关于计算允许相交的路径数量时直接 dp 的正确性

省流：大部分题解用 LGV 引理后的 dp 是错的。

rt，本题的普遍思路为：考虑起点集合 $\set{(1,2),(2,1)}$ 与终点集合 $\set{(n-1,m),(n,m-1)}$ 然后容斥，最后计算恰好覆盖所有关键点的路径对数量。但是我发现大部分题解的 dp 不正确、会算重。可能是因为最终答案为两个 dp 值相减，算重的部分两边都算重了。

以样例为例：

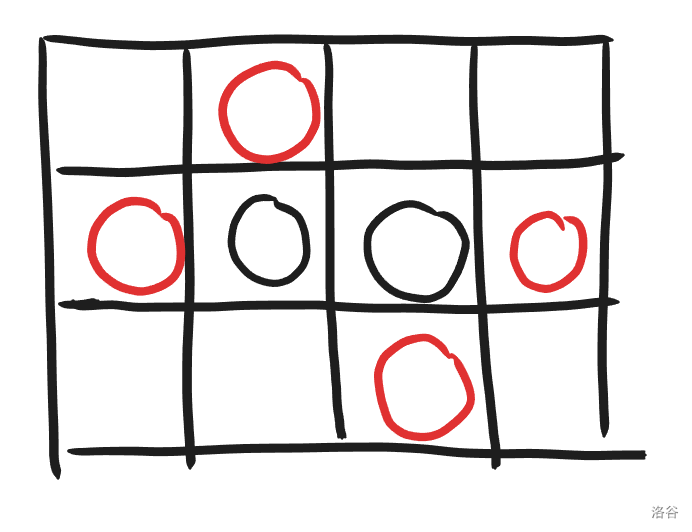
标黑的是关键点，红色的点为起点和终点。对于下面蓝色路径标出来的一种合法方案：

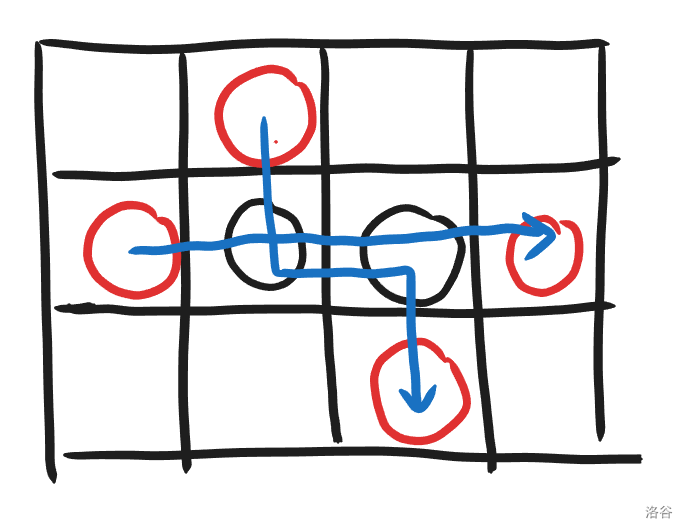
注意到，按照将所有点的 $x_i+y_i$ 排序后，用 $f(i,j)$ 表示一个到 $i$ 号关键点、另一个在 $j$ 的方案数的 dp，并且每次选择一条路径走到 $\max(i,j)+1$ 的点上，该方案会被统计两次：

结果就是，如果按照这种 dp 算方案数，单看一个 dp 状态算出的路径数量重了很多。比如一些题解在算 $2\to 6,1\to 5$ 时的答案是 $8$ 而不是理论上正确的 $3$。只有这篇用二项式定理计算的题解答案是有道理的。

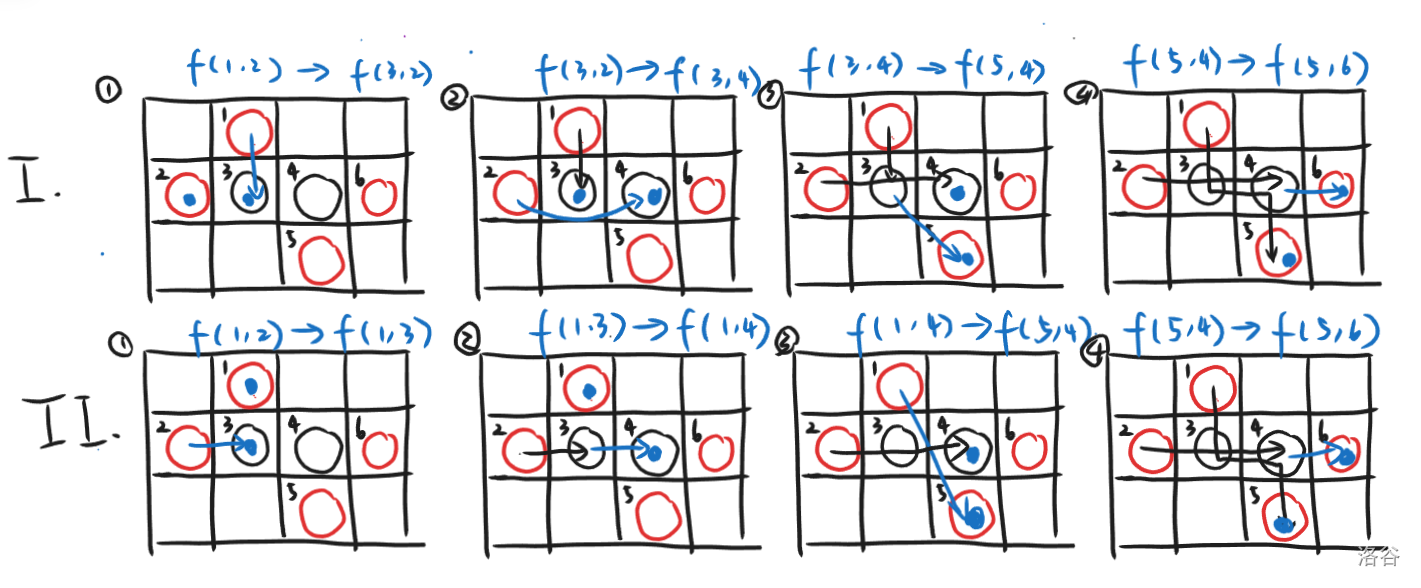
由于这题最终答案需要容斥，把重的部分又减掉了，但我觉得使用这种 dp 的题解应当要指出算重的问题。