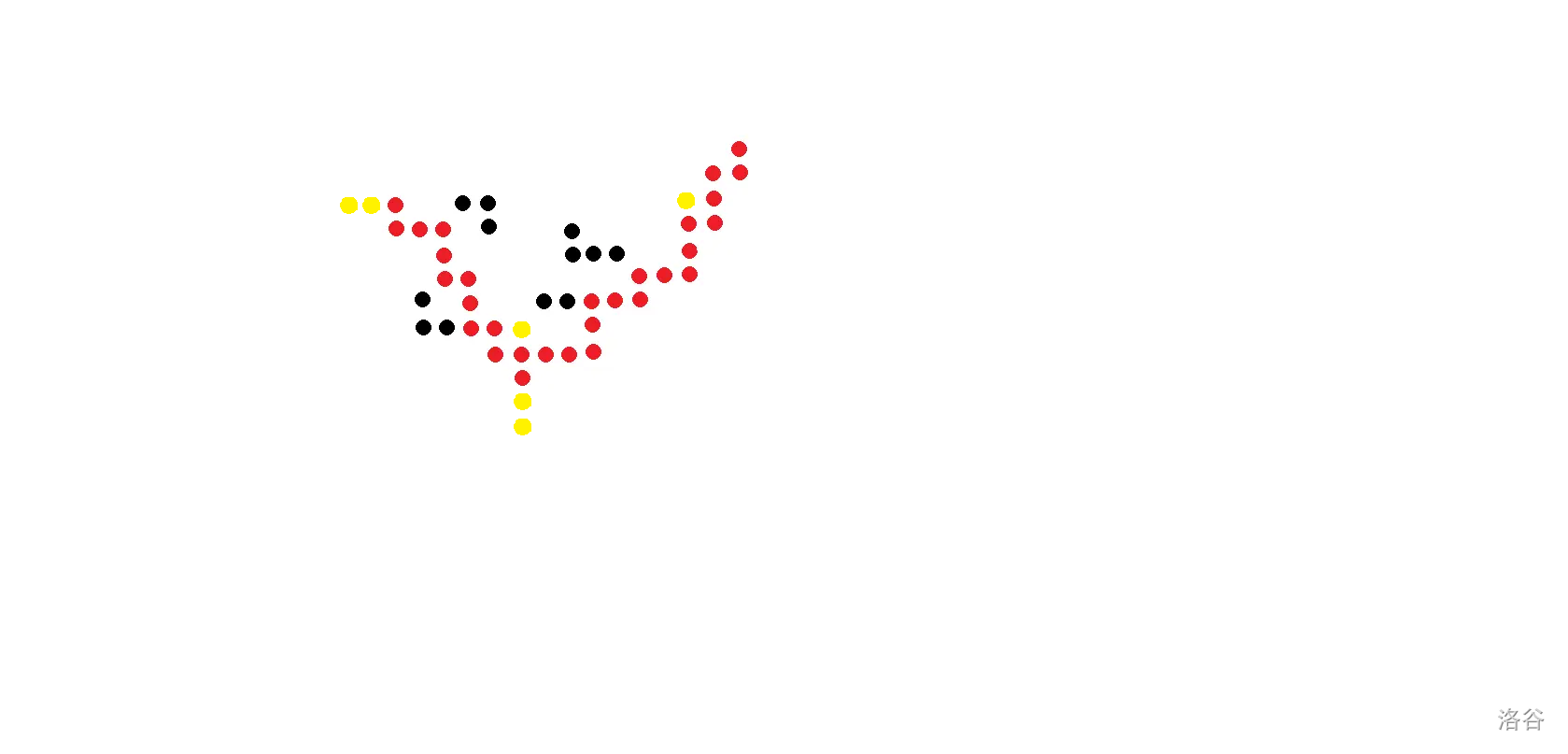求解法

$\textup{chrispang}$ 总爱在同桌互批作业时给 $\textup{lyz}$ 的作业打 √，可 $\textup{lyz}$ 偏偏不喜欢这个符号，并且给这个符号取了“根号钩”这个名字，结果每次互改作业都闹得有些不愉快。

为了让 $\textup{lyz}$ 领略 √ 的独特魅力，$\textup{chrispang}$ 在平面上标记了很多个整数点，打算从中选一些点勾勒出一个巨大的 √。这个 √ 自然是越大越有说服力，你能帮 $\textup{chrispang}$ 实现这个目标吗？

$\textup{chrispang}$ 找到了 $n$ 个整数点，请你从中选取一些点，构成一个大小为 $s$ 的点集合，其中第 $i$ 个点表示为 $x_i,y_i$，这个点集合要求存在一个整数 $k(1\le k\le s)$，使得

当然，如果仅仅是这些的话，还不足以让 $\textup{lzy}$ 心服口服。因此，$\textup{lzy}$ 让 $\textup{chrispang}$ 挑战再任意添加 $m$ 个整数点（要求添加后不可以存在重合的点）。

也就是说，$\textup{chrispang}$ 需要从 $n$ 个点中选择一些点，并且可以再添加 $m$ 个点，使得这些点满足上述要求。求问 $\textup{chrispang}$ 将会组成的 √ 最长是多少。

第一行给定两个整数，$n$ 和 $m$。

之后的 $n$ 行每行两个整数 $x_i$ 与 $y_i$，表示一个点 $(x_i,y_i)$。

输出一行一个整数，表示 $\textup{chrispang}$ 将会组成的 √ 最长是多少。

5 0
2 2
2 3
3 3
4 4
4 5

3

5 2
2 2
2 3
3 3
4 4
4 5

7

保证对于所有数据满足：$1 \leq n \leq 500$，$0 \leq k \leq 100$。对于所有给定的整点，其横纵坐标 $1 \leq x_i, y_i \leq {10}^9$，且保证所有给定的点互不重合。对于自由添加的整点，其横纵坐标不受限制。你获得的点集合可以任意排列，不需要按照题目顺序排列。

这是 √（即 $\textup{lyz}$ 命名的“根号钩”），而这是 $\sqrt{}$（即数学符号，源代码为 $\sqrt{}$）