无排序做法求卡常（可能包含部分做法）

替换基排部分为维护如下的询问序列

（令

\Delta

为整块修改的偏移量，在每一段内

Delta

不降）

考虑一个块内的所有询问操作复杂度是

O(B\sqrt n)+q

（

B

为询问段个数）。所以只要维护

B

是

\sqrt n

量级复杂度就是对的。

考虑逐块处理时从一个块向下一个块的移动造成的影响。

首先，先要把段以下一个块中散块修改的地方断开。会增加 下一个块中散修 的块数。

一次散块修改的影响如下图：

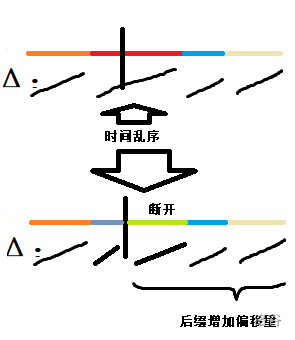
但是块数变多了，于是我们考虑设置

\sqrt n

的阈值，如果相邻的两个段的长度之和小于等于阈值，我们就归并为一个段，由于段数是

O(n)

的，所以总合并复杂度是

O(n\sqrt n)

的。

现在的程序的主要瓶颈是散块修改的线段树部分，有约 0.5s 。

可以帮忙卡下吗喵，谢谢喵。nya~

B 是序列分块
BR 是上述的阈值
B2 是线段树递归到底层改为暴力的阈值

CPP

#include<bits/stdc++.h>
#define ls(x) ((x)<<1)
#define rs(x) ((x)<<1|1)
#define N 100005
#define B 260
#define BR 600
#define B2 20
#ifdef __linux__
#define getchar() getchar_unlocked()
#define putchar(x) putchar_unlocked(x)
#endif 
#ifdef __WIN32
#define getchar() _getchar_nolock()
#define putchar(x) _putchar_nolock(x)
#endif 
using namespace std;
namespace shan{
	template<typename T>inline void read(T &x){
		x=0;char ch=' ';
		int bj=0;
		while(!isdigit(ch)){
			if(ch=='-')bj=1;
			ch=getchar();
		}
		while(isdigit(ch)){
			x=x*10+ch-'0';
			ch=getchar();
		}
		if(bj)x=-x;
	}
	typedef long long ll;
	const ll inf=4e18;
	int n,m,cnt_Q;
	int a[N];
	struct QUery{int opt,l,r,id,ex;}q[N];
	struct WAITING{
		int id,ex;
		bool operator < (const WAITING&y)const{return ex<y.ex;}
	};//维护询问
	struct dot{
		int x;ll y;
		inline ll f(const ll &v){return x*v+y;}
		dot& operator -= (const dot&o){x-=o.x;y-=o.y;return *this;}
		dot& operator += (const dot&o){x+=o.x;y+=o.y;return *this;}
	};//点
	inline dot operator + (const dot&x,const dot&y){return dot{x.x+y.x,x.y+y.y};}
	inline dot operator - (const dot&x,const dot&y){return dot{x.x-y.x,x.y-y.y};}
	inline bool operator < (const dot&x,const dot&y){return x.x*y.y<x.y*y.x;}//叉积
	inline int fix(dot *x,const int & n){//将一个点集原地置换为它的凸包，返回长度
		if(n<1)return n;
		int top=1;
		for(int i=2;i<=n;i++){
			if(x[i].y<=-1e18)continue;
			while(top>=1&&x[i]-x[top]<x[top]-x[top-1])top--;
			x[++top]=x[i];
		}
		return top;
	}
	inline int fix_dt(dot *x,const int & n){//给如给出的都是x[i+1]-x[i]的点集形式
		if(n<1)return n;
		int top=1;
		for(int i=2;i<=n;i++){
			x[++top]=x[i];
			while(top>=1&&x[top]<x[top-1]){
				x[top-1]+=x[top];
				top--;
			}
		}
		return top;
	}
	inline int getpre(const int & l,const int & r,dot *L){//前缀凸包，返回长度
		ll sum=0;for(int i=1;i<=r-l+1;i++)L[i]={i,sum+=a[l+i-1]};
		return fix(L,r-l+1);
	}
	inline int getsuf(const int & l,const int & r,dot *R){//后缀凸包，返回长度
		ll sum=0;for(int i=1;i<=r-l+1;i++)R[i]={i,sum+=a[r-i+1]};
		return fix(R,r-l+1);
	}
	inline void getcrossmid(const int & l,const int & r,dot *x,dot *L,dot *R){
		//跨越中点的部分，不保证为凸包
		const int mid=(l+r)>>1;
		for(int i=mid;i>=l;i--)L[mid-i+1]={1,a[i]};
		for(int i=1;i<=r-mid;i++)R[i]={1,a[i+mid]};
		int l1=fix_dt(L,mid-l+1),l2=fix_dt(R,r-mid);
		dot lst={0,0};
		for(int i=1,j=0,k=0;i<=l1+l2;i++){
			if(j<l1&&(k==l2||L[j+1]<R[k+1]))lst+=L[++j];
			else lst+=R[++k];
			x[lst.x].y=lst.y;
		}
		x[0]={0,0};
	}
	int st[N/B+5],ed[N/B+5],tot_B;
	dot L[B+5],R[B+5];
	dot *has[(B+5)<<2],lsl[B+5],lsr[B+5];
	int lenhas[(B+5)<<2];
	inline void push_up(const int & l,const int & r,const int & x){
		for(int i=0;i<=r-l+1;i++)has[x][i]={i,-inf};
		if(r-l+1<=B2){
			for(int i=l;i<=r;i++){
				ll sum=0;
				for(int j=i;j<=r;j++)
					has[x][j-i+1].y=max(has[x][j-i+1].y,sum+=a[j]);
			}
			//阈值以内n^2暴力
		}else{
			getcrossmid(l,r,has[x],lsl,lsr);
			for(int i=1;i<=lenhas[ls(x)];i++)
				has[x][has[ls(x)][i].x].y=max(has[x][has[ls(x)][i].x].y,has[ls(x)][i].y);
			for(int i=1;i<=lenhas[rs(x)];i++)
				has[x][has[rs(x)][i].x].y=max(has[x][has[rs(x)][i].x].y,has[rs(x)][i].y);
			//合并左右儿子答案
		}
		lenhas[x]=r-l+1;
	}
	ll lazy[(B+5)<<2];
	void build(const int & l,const int & r,const int & x){
		has[x]=new dot[r-l+2];
		lazy[x]=0;
		if(r-l+1>B2){
			int mid=(l+r)>>1;
			build(l,mid,ls(x));
			build(mid+1,r,rs(x));
		}
		push_up(l,r,x);
	}
	inline void put(const int & x,const int & ex){
		for(int i=1;i<=lenhas[x];i++)
			has[x][i].y+=(ll)ex*has[x][i].x;
		lazy[x]+=ex;
	}
	void rebuild(const int & l,const int & r,const int &ex,const int &s,const int & e,const int & x){
		if(l<=s&&e<=r){
			put(x,ex);
			return;
		}
		if(e-s+1>B2){
			if(lazy[x]){
				put(ls(x),lazy[x]);
				put(rs(x),lazy[x]);
				lazy[x]=0;
			}
			int mid=(s+e)>>1;
			if(l<=mid)
				rebuild(l,r,ex,s,mid,ls(x));
			if(mid<r)
				rebuild(l,r,ex,mid+1,e,rs(x));
		}
		push_up(s,e,x);
	}
	pair<ll,ll>ans[N];
	int lenl,lenr;
	WAITING wait[N],ls[N];
	int newid[N],at[N],att[N];
	void splitto(int now){
		//下称块内散块修改为断点
		//将每一段从断点初隔开
		memcpy(att,at,sizeof(int)*(now+1));
		for(int i=1;i<=cnt_Q;i++)
			ls[att[newid[wait[i].id]]++]=wait[i];
		memcpy(wait+1,ls+1,sizeof(WAITING)*cnt_Q);
	}
	int unable[N];
	inline void solve(int bl,int br,int ql,int qr,int dtl,int dtr){
		//计算某个断点到前一个断点之间询问的答案
		if(qr<ql)return;
		ll sum=0;
		for(int i=bl;i<=br;i++)sum+=a[i];
		lenhas[1]=fix(has[1],lenhas[1]);
		lenl=getpre(bl,br,L);lenr=getsuf(bl,br,R);
		int lst=INT_MIN;
		for(int i=ql,j=0,k=0,l=0;i<=qr;i++){
			wait[i].ex+=dtr;//上个块和我偏移量不同的
			int dt=wait[i].ex,id=wait[i].id; 
			wait[i].ex+=dtl;//下个块和我偏移量不同的
			if(unable[id])continue;
			if(dt<lst)j=k=l=0;
			while(j<lenl&&L[j+1].f(dt)>=L[j].f(dt))j++;
			while(k<lenr&&R[k+1].f(dt)>=R[k].f(dt))k++;
			while(l<lenhas[1]&&has[1][l+1].f(dt)>=has[1][l].f(dt))l++;
			ans[id].first=max(ans[id].first,max(has[1][l].f(dt),ans[id].second+L[j].f(dt)));
			ans[id].second=max(ans[id].second+sum+(ll)dt*(br-bl+1),R[k].f(dt));
			lst=dt;
		}
	}
	void fix(){
		//合并较小的块，维护复杂度
		ll lst=-inf;
		int lstl=0,lstr=0;
		int nowl=1,nowr=0;
		for(int i=1;i<=cnt_Q;i++){
			if(wait[i].ex<lst){
				if(lstr&&nowr-nowl+lstr-lstl+2<=BR)
					inplace_merge(wait+lstl,wait+nowl,wait+nowr+1);
				else
					lstl=nowl;
				lstr=nowr;
				nowl=i;
			}
			nowr=i;
			lst=wait[i].ex;
		}
	}
	int CNT;
	signed main(){
		read(n);read(m);
		for(int i=1;i<=n;i++){
			read(a[i]);
			tot_B=(i-1)/B;
			if(!st[tot_B])
				st[tot_B]=i;
			ed[tot_B]=i;
		}
		for(int i=1;i<=m;i++){
			read(q[i].opt);
			read(q[i].l);
			read(q[i].r);
			if(q[i].opt==1)
				read(q[i].ex);
			else
				q[i].id=++cnt_Q;
		}
		for(int i=1;i<=cnt_Q;i++)wait[i].id=i;
		at[0]=1;
		for(int i=0;i<=tot_B;i++){
			int mL=st[i],mR=ed[i];
			build(mL,mR,1);
			int now=0,now_q=0;
			//先得到断开方式
			for(int j=1;j<=m;j++){
				if(q[j].opt==1){
					if(q[j].r>=mL&&q[j].l<=mR&&(q[j].l>=mL||mR>=q[j].r))at[++now]=now_q+1;
				}else{
					newid[++now_q]=now;
					unable[now_q]=q[j].r<mR||q[j].l>mL;
				}
			}
			at[now+1]=now_q+1;
			splitto(now);
			int dt=0,dtl=0,dtr=0;
			for(int j=1,now=0;j<=m;j++){
				if(q[j].r<mL||q[j].l>mR)continue;
				if(q[j].opt==1){
					if(q[j].l<mL&&mR<q[j].r){
						dt+=q[j].ex;
					}else{
						//散块修改
						now++;
						//上个断点和我之间的询问
						solve(mL,mR,at[now-1],at[now]-1,dtl,dtr);
						if(!q[j].ex)continue;
						if(mR<q[j].r)dtl+=q[j].ex;//左端点
						if(q[j].l<mL)dtr-=q[j].ex;//右端点
						int ST=max(mL,q[j].l),ED=min(mR,q[j].r),ex=q[j].ex;
						CNT+=ED-ST+1;
						//改序列
						for(int k=ST;k<=ED;k++)a[k]+=ex;
						//改树上
						rebuild(ST,ED,ex,mL,mR,1);
					}
				}else{
					if(q[j].l>mL||mR>q[j].r){
						ll minn=0,sum=0;
						for(int k=max(mL,q[j].l);k<=min(mR,q[j].r);k++){
							sum+=a[k]+dt;
							minn=min(minn,sum);
							ans[q[j].id].first=max(ans[q[j].id].first,max(sum-minn,ans[q[j].id].second+sum));
						}
						if(q[j].r>mR){
							sum=0;
							for(int k=mR;k>=q[j].l;k--)
								ans[q[j].id].second=max(ans[q[j].id].second,sum+=a[k]+dt);
						}
					}
				}
			}
			solve(mL,mR,at[now],now_q,dtl,dtr);
			if(!(i%20))fix();
		}
		for(int i=1;i<=cnt_Q;i++)
			cout<<ans[i].first<<'\n';
		cerr<<CNT;
		return 0;
	}
} 
signed main(){
	ios::sync_with_stdio(false);cin.tie(0);
	shan::main();
	return 0;
}

lastrecord

无排序做法求卡常（可能包含部分做法）

讨论操作

回复

相关推荐

无排序做法求卡常（可能包含部分做法）