专栏文章

杂题乱刷备份9.19

TTLE_Automat
题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mio7ep6e
此快照首次捕获于
2025/12/02 14:35
3 个月前
此快照最后确认于
2025/12/02 14:35
3 个月前
查看原文

待筛选题目

LuoguP2178【字符串，紫】（二周目复习，强制使用 SAM 来做）
CF141D【图论，*2300】
CF960H【数据结构，*3100】
https://codeforces.com/problemset/problem/2140/D
https://codeforces.com/problemset/problem/2138/B
https://codeforces.com/problemset/problem/2131/F
https://codeforces.com/problemset/problem/2128/E2

已筛选准备思考+看题解

待写题解

LuoguP11202【动态规划，蓝】
ICPC2023 EC-Final Shanghai J【图论|交互，72/280】

已写题解，待完成代码

LuoguP11726【图论，蓝】| LuoguP9331【图论，紫】

已完成

LuoguP10544【动态规划，紫】| LuoguP11536【数据结构，紫】| CF1422D【*2300】| LuoguP6478【数学，紫】| LuoguP7406【动态规划，蓝】| LuoguP2605【动态规划，紫】| LuoguP6475【数学，蓝】| LuoguP5339【数学，紫】| CCPC2024 重庆站 D【数学，66/278】| LuoguP4022【字符串，黑】| LuoguP5377【数学，蓝】| LuoguP11203【数据结构，紫】| CF997E【数据结构，*3000】| LuoguP8386【动态规划，紫】| LuoguP4657【动态规划，紫】| ICPC2024 上海站 J【数据结构，12/352】| ICPC2023 EC-Final Shanghai C【dp，8/280】

数据结构

Luogu P11536 [NOISG 2023 Finals] Curtains 洛谷难度评级【紫】
第一反应是先按顺序把每个区间的右端点挂到 vector 里，然后按右端点从小到大做扫描线，这样每个区间的右端点肯定不超，就只需要考虑左端点超不超的问题了。
考虑维护每个区间的左端点 LL 向右跳最远能跳到的位置 tLt_L，如果扫描线扫到 eie_i 时 tsi=eit_{s_i} = e_i 则说明区间 [si,ei][s_i, e_i] 满足条件。
每次扫描线向右移动时，假设新添加了区间 [l,r][l, r]，那么对于所有满足 tj+1≥lt_j + 1 \ge l 的 tjt_j，将其更新为 rr。相当于区间对 ≥x\ge x 的数重新赋值为 y,y>xy, y > x，且 yy 单调递增。这个可以用类似 sg beats 的方法，用带两个 log⁡\log 的时间复杂度维护出来。
考虑另外一种做法，还是先按右端点扫描线，但是对于每个位置 pp 维护出包含位置 pp 的所有区间中 ll 的最大值，记为 fpf_p。
假设当前扫描线扫到 eie_i 了，当且仅到 min⁡sitifp=ei\min_{s_i}^{t_i} f_p = e_i 时，区间 [si,ti][s_i, t_i] 才能被覆盖。直接线段树维护区间取 max⁡\max，区间求 min⁡\min 即可，时间复杂度为 O(n+(m+q)log⁡n)O(n + (m + q)\log n)。
</> https://www.luogu.com.cn/record/232015123
Luogu P11203 [JOIG 2024] 感染シミュレーション / Infection Simulation 洛谷难度评级【紫】
注意到一个性质，餐厅中存在感染者的时间一定是一段连续的区间，如果某个时间餐厅中没有感染者了，传染源消失，在餐厅的人还没被感染，之后肯定也不会出现新的被感染的人。
假设感染者存在的时间为 [L,R][L, R]，那么第 ii 个人被感染的条件为 ri−x≥L\andri≤R\andri−li≥xr_i - x \ge L \and r_i \le R \and r_i - l_i \ge x，不妨令 leni=ri−lilen_i = r_i - l_i，则以上条件可以写为 L+x≤ri≤R\andleni≥xL + x\le r_i \le R \and len_{i} \ge x。这是一个二维偏序问题，我们可以按 lenilen_i 排序，建立以 rir_i 为值域的可持久化线段树，每次查询二分出 leni≥xlen_i \ge x 的部分，然后查询区间 [L+x,R][L + x, R] 上的贡献即可。
现在的问题是怎么求出 [L,R][L, R]。由于时光不能倒流，所以 LL 一定是初始被感染者的区间的左端点。
考虑维护一个当前存在感染者的右边界 curRcurR，发现这个右边界能够向右扩展的条件是，找到一个 ii 满足 ri>curRr_i > curR，且 lil_i 最小，如果 curR−li≥xcurR - l_i \ge x，那么感染就可以向右扩展到 rir_i（这是感染边界向右扩展的最宽松的条件，如果感染最终的边界为 Rmax⁡R_{\max}，那一定可以通过这种方法扩展得到）。
虽然每次询问的 xx 不同，但我们能根据上述方法，处理出能使某个区间向右扩展一次的最大的 xx，及其扩展到的区间的右边界。在此基础上就可以倍增预处理出 fp,if_{p, i} 代表从能使得从区间 pp 开始向右扩展 2i2^{i} 次的最大的 xx。这样每次询问的时候就可以根据当次询问的 xx，倍增求出最远能扩展到的 Rmax⁡R_{\max}。
总时间复杂度 O((N+Q)(log⁡N+log⁡V))O((N + Q)(\log N + \log V))。
</> https://www.luogu.com.cn/record/234226093
CF997E CF难度评级【*3000】
首先不难注意到好的区间一定满足 mx−mn=r−lmx - mn = r - l，但是只有这个性质求不出来什么东西。又注意到任意一段区间一定满足 mx−mn≥r−lmx - mn \ge r - l，即 (mx−mn)−(r−l)≥0(mx - mn) - (r - l) \ge 0，好的区间刚好取到了最小值 00，我们只需要想办法维护最小值 00 的个数。
考虑扫描线从左到右扫描右端点 rr，可以使用两个单调栈分别维护以 rr 为右端点 ii 为左端点的每个区间的 mx,mnmx, mn，然后在线段树上区间加减，rr 每次向右移动直接将 11 到 r−1r - 1 的值全部区间减 11 即可。
但是我们要查询的并不是某个固定的右端点 rr 的区间，而是一段区间中的所有子区间，所以线段树不仅要维护区间中当前 00 的个数，还要想办法维护区间历史出现 00 的总次数，同时还要支持区间加减操作。
因为题目的性质保证了一个位置最小只能被减到 00，不可能被减到更小，所以如下图一样设计线段树维护的信息和懒标记。
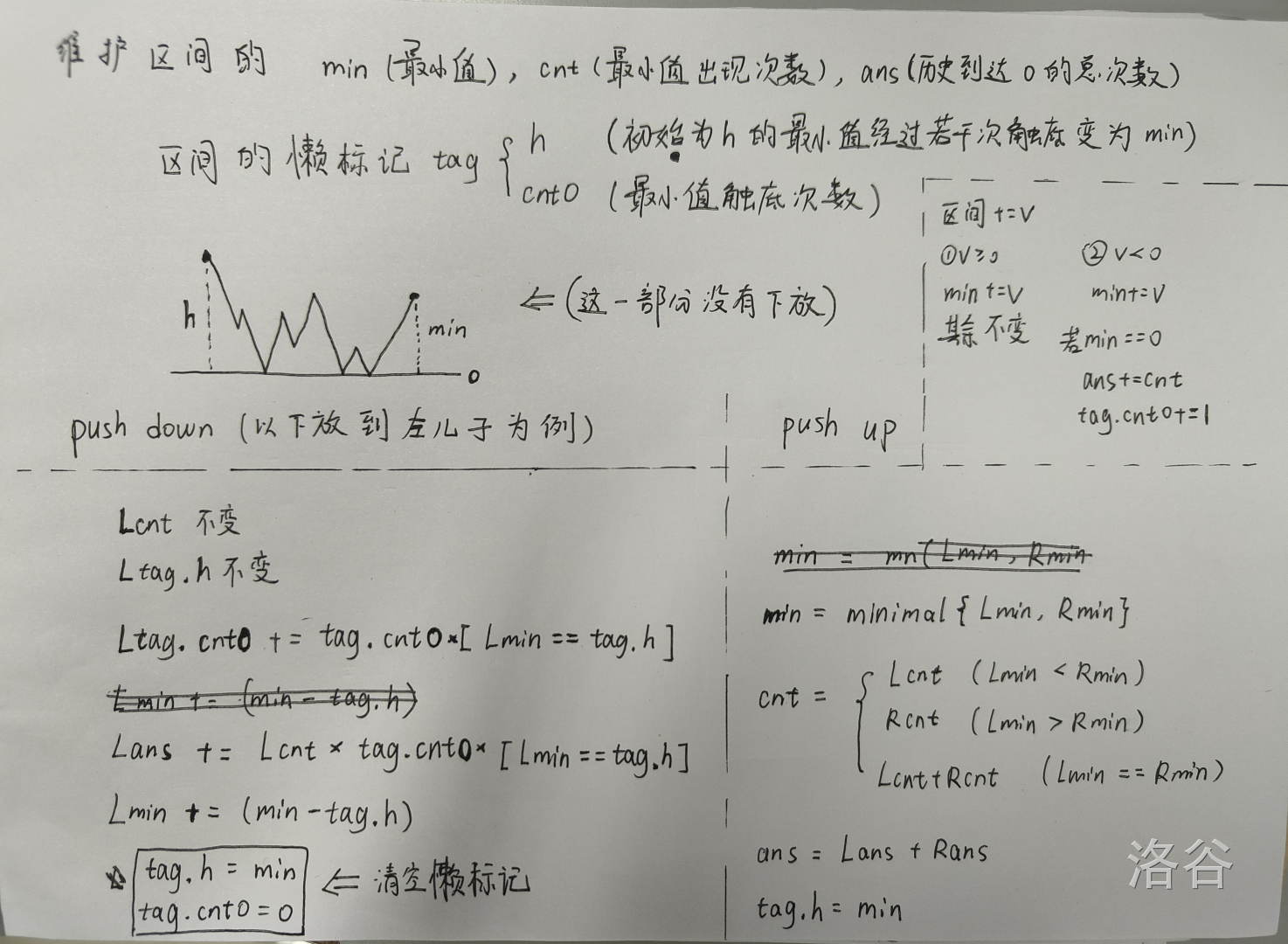
总时间复杂度 O((n+q)log⁡n)O((n + q)\log n)。
</> https://codeforces.com/contest/997/submission/337002673
ICPC2024 上海站 J.Just-in-Time Render Analysis 赛时通过【12/352】
先考虑怎么把矩形的嵌套转化成树的结构，由于嵌套的矩形之间没有交，我们可以按 xx 扫描，用一个 set 来维护一个类似于线段覆盖的东西，遇到矩形的左边界就插入这条线段，遇到矩形的右边界就删除这条线段，如果这条线段被 set 中的某条线段覆盖了，那就将其连到父节点上，并将覆盖的线段分裂，删除被覆盖的线段的时候再将覆盖的线段合并。
若一个结点 xx 被打开，我们就将从 xx 到根的路径上的点的点权 +1+1，若一个结点 xx 被关闭，我们就将 xx 到根的路径上的点的点权 −1-1，我们需要维护的是每一层有多少个点权值大于 00。
注意到从任意一个结点 xx 到根的路径上的结点权值单调非降，所以对每个点 xx 修改时，权值从 11 变为 00 或者从 00 变为 11 的结点的深度一定时从 depxdep_x 向上的一个连续段，于是我们先树剖，然后用线段树维护区间的最小值和最小值个数，这样就能知道从 depxdep_x 向上的连续段具体有多长了，再开一个树状数组维护答案关于深度的差分即可。总时间复杂度 O((n+q)log⁡2n)O((n+q)\log^2n)。
</> https://qoj.ac/submission/1361879

动态规划

Luogu P10544 [THUPC 2024 决赛] 转化 洛谷难度评级【紫】
这题有一个使用 tarjan 缩强连通分量再做的方法，但细节巨多，所以我选择记录一个比较暴力的使用 dp 的方法。
假设进行了 tt 次转化，我们把 nn 种物品复制 tt 层，每一层向上一层的若干点连边（转移），表示一次转化，这样我们就可以设 fi,tf_{i, t} 代表物品 ii 经过 tt 层的转化最多转化成多少物品 dd，枚举 mm 种转化，这样就能实现从 t−1t - 1 层向 tt 层的转移。
初始值为 fd,0=1f_{d, 0} = 1，其他都为 00。当对于所有的 1≤i≤n,fi,t=fi,t−11\le i\le n, f_{i, t} = f_{i, t - 1} 时，即 ff 收敛时，就说明再转移也不会变得更优了，此时迭代完成。
考察答案可以无限大的情况，这种情况下的最优转移过程在原图的中间一定至少有一个环，通过在这个环上一直旋转来不断产生输出；同理，如果答案有限，那中间一定不存在环（最终的 dd 可能在一个每个点的出度等于 11 环上，但这个并不会使答案无限增大），不存在环意味着这个 tt 层的转移 DAG 上的任意一条链都不包含重复的点，那么此时 tt 就不会超过 nn。
以上的证明意味着 ff 要么在 t≤nt \le n 时收敛，要么永远发散，所以 dp 时 tt 只需枚举到 nn 即可。总时间复杂度 O(n3m)O(n^3m)，常数极小可以通过。
</> https://www.luogu.com.cn/record/231579801
Luogu P7406 [JOI 2021 Final] 集体照 / Group Photo 洛谷难度评级【蓝】
由于 pp 是一个排列且满足 1≤i<n,pi≤pi+1+11 \le i < n, p_i \le p_{i + 1} + 1，那么 pp 一定是若干段连续下降的区间，且若把每一段看成一个整体，容易发现段之间是单调增的。
容易证明，这个东西等价于一个 1,2,⋯ ,n1, 2, \cdots, n 的数列分成若干段区间反转，如下图所示。
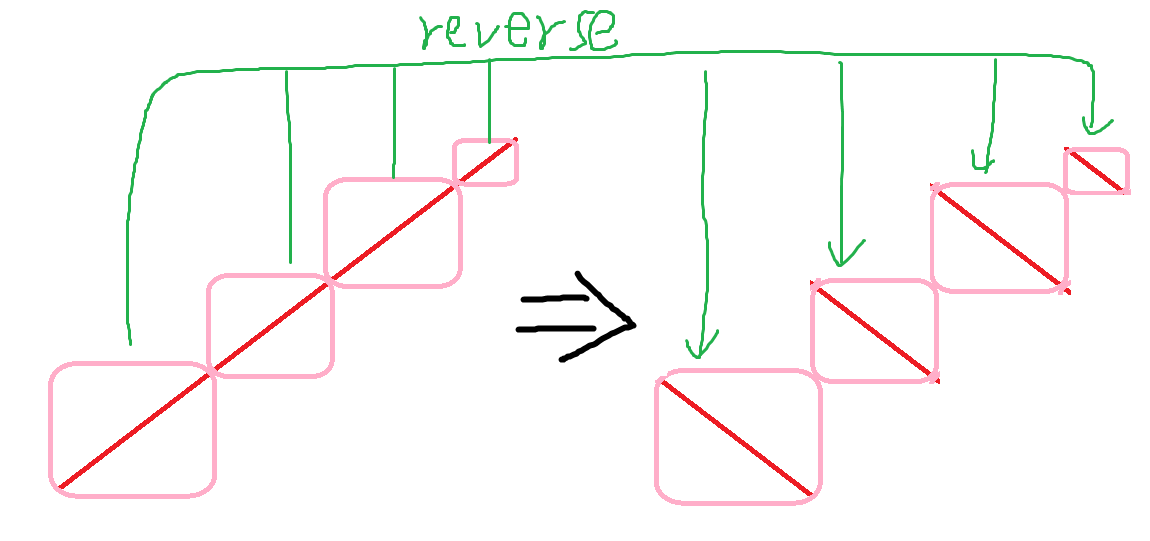
可以发现一个性质，就是在每段结束的位置 pospos，前面出现的所有数字一定是 11 到 pospos，因为前面的序列就是 1,2,⋯ ,pos1,2,\cdots,pos 的分段 reverse。
那么可以设 fif_i 为钦定 ii 这个位置是某一段的结束的最少交换次数，然后枚举下一段的长度 ll，显然下一段就是 i+li + l 到 i+1i + 1 的一个连续下降序列，最优的交换次数可以用树状数组贪心地求出，最终答案为 fnf_n。时间复杂度为 O(n2log⁡n)O(n^{2}\log n)。
</> https://www.luogu.com.cn/record/232900633
Luogu P2605 [ZJOI2010] 基站选址 洛谷难度评级【紫】
一道非常古老的 ZJOI 的题目，但是 dp 的优化方法放在现在来看依然很有借鉴意义。
先考虑一个暴力 dp，令 fi,jf_{i, j} 表示到前 ii 个点建了 jj 个基站，且钦定第 ii 个点建了基站的最小代价。如果直接暴力枚举上一个基站建立的位置 pp，可以做到 O(n2k)O(n^{2}k)。
之所以要枚举上一个基站建在哪里，是因为我们必须确定了第 j−1j - 1 个和第 jj 个基站的位置，才能计算夹在中间的未被基站覆盖到的村庄的代价。
对于这一类问题，这道题目给了我们一个启示，就是我们可以把中间的代价直接黏附到左边的 dp 值上。
具体地，对于一个村庄 ii，如果区间 [di−si,di+si][d_{i} - s_{i}, d_{i} + s_{i}] 上没有基站，就会产生 wiw_i 的代价。将这些区间先按右端点 di+sid_i + s_i 从小到大排序，dp 过程中用类似双指针的方法枚举夹在中间的区间 ii ，对于 p<di−sip < d_{i} - s_{i} 的所有 fp,jf_{p, j} 整体加上 wiw_i，相当于把额外产生的代价黏到了左边的 dp 值上，转移的时候只要查 ff 的前缀最小值，可以使用线段树轻松维护。总时间复杂度 O(nklog⁡n)O(nk\log n)。
</> https://www.luogu.com.cn/record/233399353
Luogu P8386 [PA 2021] Od deski do deski 洛谷难度评级【紫】
序列计数问题，一般的套路是考虑向序列最后添加一个新的数字。
考虑怎么检验一个给定的序列 aa 是否合法，对于每个可以删除的前缀 a1⋯ia_{1\cdots i}，可以把 ai+1a_{i + 1} 的值放到集合 SS 中，到位置 jj 时，如果 SS 中有与 aja_j 相同的元素，那么说明 a1⋯ja_{1\cdots j} 的前缀也能删除，再把 aj+1a_{j + 1} 的值放入集合 SS 中重复上述过程。
根据上述检验的过程，位置 ii 要满足匹配/不匹配，aia_i 的取值只与集合 SS 的大小有关，所以这启发我们维护集合 SS 的大小。
设 fi,j,0/1f_{i, j, 0/1} 代表已经确定了前 ii 个位置的取值，集合 SS 大小为 jj，a1⋯ia_{1\cdots i} 是否能删除，的总方案数，讨论下一个位置的取值即可 O(1)O(1) 转移，具体转移如下：
fi+1,j,0←fi,j,0×(m−j)fi+1,j+1,0←fi,j,1×(m−j)fi+1,j,1←(fi,j,0+fi,j,1)×j\begin{aligned} f_{i + 1, j, 0} &\leftarrow f_{i, j, 0} \times (m - j) \\ f_{i + 1, j + 1, 0} &\leftarrow f_{i, j, 1} \times (m - j) \\ f_{i + 1, j, 1} &\leftarrow (f_{i, j, 0} + f_{i, j, 1}) \times j \end{aligned}
因为每个位置最多向集合 SS 中添加一个新元素，所以集合 SS 的大小最大为 nn，总时间复杂度 O(n2)O(n^2)。
</> https://www.luogu.com.cn/record/234973351
Luogu P4657 [CEOI 2017] Chase 洛谷难度评级【紫】
为避免混淆，题目中的 VV 在下文中将会使用 dd 表示。
对于这种找满足某种条件的最大值路径的问题，一般套路是树形 dp。由于本题的性质，若在结点 uu 上放了磁铁，那么会对答案产生路径上结点 uu 的下一个结点 nxtunxt_u 的贡献。
所以我们把 dp 分成沿路径上行的和沿路径下行的，那么可以令 fu,i,0/1,gu,i,0/1f_{u, i, 0/1}, g_{u, i, 0/1} 分别代表以 uu 为根节点，沿路径上行/下行，已经放了 ii 个磁铁，结点 uu 有没有放磁铁，的路径的最大贡献。因为若一个结点 uu 放了磁铁，会产生与 uu 相邻的且不在路径上的结点的权值的贡献，于是可以预处理出 valuval_{u} 表示与 uu 相邻的所有结点的权值之和来方便转移。
然后就是枚举 u,iu, i 及 uu 的两个不同的儿子 v1,v2v_1, v_2 然后合并 fv1,i,0/1f_{v_1, i, 0/1} 和 gv2,d−i/d−i−1,0/1g_{v_2, d - i/d-i-1, 0/1}，可以讨论 uu 这个结点放不放磁铁，然后提前维护 gv,i,0/1g_{v, i, 0/1} 对于每个 ii 的最大值和次大值，这样对于每一个 u,iu, i 就可以只枚举 v1v_1，然后 v2v_2 直接取最大或次大即可。总时间复杂度 O(nd)O(nd)。
</> https://www.luogu.com.cn/record/235064155
ICPC2023 EC-Final Shanghai C. Equal Sums 赛时通过【8/280】
考虑 dp 里存 xx 的前缀和 yy 的前缀的差，差等于 00 的方案数即为最终的答案，但直接这样 dp 是 O(n4)O(n^4) 的。
因为 x,yx,y 的值域都是 [1,500][1, 500]，所以 x,−yx, -y 的任意两个和等于 00 的前缀，它们一定能拼成一个序列 pp，使得 pp 的任何一个位置的前缀和都在 [−500,500][-500, 500] 之内。
但是有很多种拼法，比如 x1=3,x2=2,−y1=−3,−y2=−2x_{1} = 3,x_{2} = 2, -y_{1} = -3, -y_{2} = -2 可以拼出 {3,2,−3,−2},{3,−3,2,−2},{−3,3,2,−2},{3,−3,−2,2},{−3,3,−2,2},{−3,−2,3,2}\{3, 2, -3, -2\},\{3,-3,2,-2\},\{-3,3,2,-2\}, \{3, -3, -2, 2\}, \{-3, 3, -2, 2\}, \{-3, -2, 3, 2\} 共 66 种，但是我们只希望统计一种，所以我们钦定如果当前的前缀和 ≥0\ge 0，就放 −y-y，如果 <0< 0 就放 xx，那么就有了唯一顺序，上面例子的顺序即 {−3,3,−2,2}\{-3, 3, -2, 2\}。
有了以上的钦定，任意一个合法的答案，一定会恰好被统计一次，这样我们 dp 的第三维就只需要维护 O(n)O(n) 个状态，再利用前缀和优化 dp，即可把总时间复杂度优化到 O(n3)O(n^{3})。

图论

CF1422D CF难度评级【*2300】
显然有一个暴力做法，就是传送门之间两两连边，然后跑最短路，但这样做边数是 O(m2)O(m^2) 级别的。
考察什么时候从一个传送门 p1p_1 直接向另外一个传送门 p2p_2 连边是必要的。发现 p2p_2 一定是上下左右四个方向的某个方向上距离 p1p_1 最近的传送门，否则可以从 p1p_1 开始每次直接走到这个方向上最近的传送门再传送，最终再走到 p2p_2 也是等价的。
所以直接按照横坐标排序依次连边，再按纵坐标排序一次连边，跑最短路即可，时间复杂度 O(mlog⁡m)O(m\log m)。
</> https://codeforces.com/contest/1422/submission/334620405
Luogu P11726 [JOIG 2025] 最悪の記者 5 / Worst Reporter 5 洛谷难度评级【蓝】
由于是从一个不确定的排列，通过若干次交换相邻项的操作得到另外一个排列，所以把操作序列反过来也等价，这样就能直接思考满足条件的初始排列的最小字典序。
考虑能否把限制通过某种方式等价成对于初始排列的限制，答案是还真能。由于交换数字 x,yx, y 时 x,yx, y 在当前排列中一定相邻，又因为我们可以通过已经进行完的交换操作推出数字 xx 在初始排列中某个数字 kk 的位置，我们将其记为 px=kp_x = k，这样能交换数字 x,yx, y 的限制就变为了初始排列中 pxp_x 与 pyp_y 一定相邻，然后再交换 px,pyp_x, p_y 即可。
把初始排列中产生限制的点之间连边，如果有结点的度数大于 22 或者出现环，那么肯定无解，否则一定是一堆链，贪心地从两头依次取字典序最小的即可。时间复杂度 O(N+M)O(N + M)。
Luogu P9331 [JOIST 2023] 护照 / Passport 洛谷难度评级【紫】
从任意一个点出发，可达的点一定构成一段区间，所以问题等价于走到 11 和 nn 最少需要经过的点数。
由于 ii 能走到区间 [Li,Ri][L_i, R_i]，可以通过线段树优化建图，建一个反图，然后分别算出从 11 和 nn 走到任意点 ii 的最短路 dis⁡1(i)\operatorname{dis}_{1}(i) 和 dis⁡n(i)\operatorname{dis}_{n}(i)。
显然这并不一定是最优解，因为从 11 到 ii 和从 nn 到 ii 的路径上的一部分点可以重合。
考虑最优解的特征。如果某一时刻，第一次在区间中选出两个点 x,yx, y，那么两个点肯定不会往同一个方向走（因为往同一个方向走选一个更优的即可，没必要选两个），假设 xx 是用来走到 11 的，yy 是用来走到 nn 的，那么之后一定是各走各的不会回头，如果最优解中 xx 回头选了一个新的更优的 y′y'，那么之前的 yy 是没有必要选的，因为可选的 yy 的集合是逐渐扩大的，反之x,yx, y 互换也同理。
综上，最优解一定是先走一段相同的点然后再分裂。令 fi=dis⁡1(i)+dis⁡n(i)f_i = \operatorname{dis}_{1}(i) + \operatorname{dis}_{n}(i)，那么 fif_i 相当于从点 ii 分裂后的代价。如果先从 ii 跳到 jj 再分裂，那么代价为 fj+1f_j + 1。令最终点 ii 的答案为 gig_i，不难看出最终答案 gi=min⁡(fi,gj+1)g_i = \min(f_{i}, g_{j} + 1)，这样子直接在原本的线段树建的反图上跑一个 gg 的全源最短路即可。时间复杂度 O(nlog⁡2n)O(n\log^{2}n)，线段树和最短路分别贡献一个 log⁡\log。

数学

Luogu P6478 [NOI Online #2 提高组] 游戏 洛谷难度评级【紫】
一个非常有启发意义的经典二项式反演。
以点 uu 为根，在其中钦定 kk 对互不重合的“祖先-后代”关系，记这个方案数为 fu,kf_{u, k}，可以通过树形背包得到。
考虑以 11 为根的整颗树，除了钦定的 kk 对节点，还有剩下的 m−km - k 对结点，这些结点之间连边的方案数为 (m−k)!(m - k)!。
令 gig_i 代表恰好有 ii 个非平局回合的方案数，可以得到
f1,k×(m−k)!=∑i=km(ik)gi\begin{aligned} f_{1, k}\times(m - k)! = \sum_{i = k}^{m}\binom{i}{k}g_{i} \end{aligned}
这是一种经典的组合意义上的对等。左边式子中 kk 对匹配的每一种方案，在所有包含它的集合中都产生了一次贡献，等价于求每一种情况被多少个集合包含，然后求和。右边式子等价于求一个集合包含了多少种情况，然后求和。如果把两边的关系看成一个二分图，那两边式子的本质就是求中间的边的数量，显然是等价的。
于是利用二项式反演即可推出答案
gk=∑i=km(−1)i−k(ik)f1,i×(m−i)!\begin{aligned} g_{k} = \sum_{i = k}^{m}(-1)^{i - k}\binom{i}{k} f_{1, i}\times(m - i)! \end{aligned}
</> https://www.luogu.com.cn/record/232825225
Luogu P6475 [NOI Online #2 入门组] 建设城市 洛谷难度评级【蓝】
先考虑暴力 dp，设 fi,jf_{i, j} 代表长度为 ii，最后一个楼层高度为 jj 的方案数，有转移
fi,j=∑k=1jfi−1,k=fi−1,j+fi,j−1\begin{aligned} f_{i, j} = \sum\limits_{k = 1}^{j} f_{i - 1, k} = f_{i - 1, j} + f_{i, j - 1} \end{aligned}
边界条件是 f1,j=fj,1=1f_{1, j} = f_{j, 1} = 1，注意到两个转移分别是从左边和上边转移过来，所以旋转一下就是杨辉三角。
具体地，令 Ci+j−2,j−1=fi,jC_{i + j - 2, j - 1} = f_{i, j}，带入递推式可得 Ci+j−2,j−1=Ci+j−3,j−1+Ci+j−3,j−2C_{i + j - 2, j - 1} = C_{i + j - 3, j - 1} + C_{i + j - 3, j - 2}，令 p=i+j−2,q=j−1p = i + j - 2, q = j - 1 可得 Cp,q=Cp−1,q+Cp−1,q−1C_{p, q} = C_{p - 1, q} + C_{p - 1, q - 1}，边界条件为 Cp,0=1C_{p, 0} = 1，这就是组合数，fi,j=(i+j−2j−1)f_{i, j} = \binom{i + j - 2}{j - 1}，先预处理出组合数，之后枚举 x,yx, y 的高度即可，时间复杂度 O(n+m)O(n + m)。
上面这个方法太不优美了，有没有什么更优美的做法呢？有的，兄弟，有的。
最优美的做法肯定是组合意义。考虑把前 i−1i - 1 个楼排成一排，然后分成 jj 段，每一段允许为空，钦定第 xx 段的高度为 xx，发现这样子就完美解决了高度不降的问题，而且这个东西就是隔板法，方案数为 (i+j−2j−1)\binom{i + j - 2}{j - 1}。
上面两种方法太吃操作了，有没有什么更加无脑的做法呢？有的，兄弟，有的。
考虑二元生成函数 F(x,y)=∑fi,jxiyjF(x, y) = \sum f_{i, j}x^{i}y^{j}，根据递推式和边界条件可得
F(x,y)=xF(x,y)+yF(x,y)+xyF(x,y)=xy1−(x+y)\begin{aligned} F(x, y) &= xF(x, y) + yF(x, y) + xy \\ F(x, y) &= \frac{xy}{1 - (x + y)} \\ \end{aligned}
然后要求的 fi,jf_{i,j} 就是
[xiyj]F(x,y)=[xi−1yj−1]F(x,y)xy=[xi−1yj−1]∑k(x+y)k=(i+j−2j−1)\begin{aligned} \left[x^{i}y^{j}\right]F(x, y) = [x^{i-1}y^{j-1}]\frac{F(x, y)}{xy} = [x^{i-1}y^{j-1}]\sum\limits_{k}(x + y)^{k} = \binom{i + j - 2}{j - 1} \end{aligned}
最无脑的推法，但是稍微需要一点无穷级数的前置知识。
</> https://www.luogu.com.cn/record/233587563
Luogu P5339 [TJOI2019] 唱、跳、rap和篮球 洛谷难度评级【紫】
考虑容斥是否可行，定义某个位置 pp 不合法为 p,p+1,p+2,p+3p, p + 1, p + 2, p + 3 分别喜欢唱、跳、rap 和篮球，现在钦定不合法的位置有 ii 个，我们发现相邻两个不合法的位置之间的距离一定大于 33，否则交集一定是空集。
可以设 fi,j,1/2/3/0f_{i, j, 1/2/3/0} 代表前 ii 个位置选出 jj 个不合法的位置，上一个不合法的位置的起点在 i,i−1,i−2i, i - 1, i - 2 或者更靠前，这样就能知道 i+1i + 1 是否可以钦定为不合法的位置，就可以转移了，这一部分的时间复杂度为 O(n2)O(n^{2})。
解决了不合法位置的钦定问题，考虑一下剩下位置的方案数怎么解决。首先可以算出剩下了 n−4in - 4i 个位置，并且唱、跳、rap 和篮球分别剩下了 a−i,b−i,c−i,d−ia - i, b - i, c - i, d - i 个，要从这里面选出来 n−4in - 4i 个并进行排列，同种之间没有区别，如果直接暴力枚举是 O(abc)O(abc) 的，再乘上枚举 ii 的 O(min⁡(a,b,c,d))O(\min(a, b,c, d)) 的复杂度，是无法通过的。
由于同种之间没有区别可以任意排列，上面这个东西可以写成指数生成函数的形式
[xn−4i(n−4i)!]F(x,a−i,b−i,c−i,d−i)=[xn−4i(n−4i)!](∑j=0a−ixjj!)(∑j=0b−ixjj!)(∑j=0c−ixjj!)(∑j=0d−ixjj!)\begin{aligned} \left[\frac{x^{n-4i}}{(n-4i)!}\right]F(x,a-i,b-i,c-i,d-i) = \left[\frac{x^{n-4i}}{(n-4i)!}\right]\left(\sum\limits_{j=0}^{a - i} \frac{x^{j}}{j!}\right)\left(\sum\limits_{j=0}^{b - i} \frac{x^{j}}{j!}\right)\left(\sum\limits_{j=0}^{c - i} \frac{x^{j}}{j!}\right)\left(\sum\limits_{j=0}^{d - i} \frac{x^{j}}{j!}\right) \end{aligned}
可以先暴力多项式乘法，分别合并左边两项和右边两项，假设合并完了是 F1,F2F_1,F_2，然后再枚举 F1F_1 的每一项，就能算出来 F1F2F_{1}F_{2} 的 xn−4ix^{n - 4i} 项的系数，这部分的时间复杂度为 O(ab+cd+a+b)=O(ab+cd)O(ab + cd + a + b) = O(ab + cd)。
最后算答案的容斥式子为
∑i=0min⁡(a,b,c,d,n)(−1)ifn,i,0(n−4i)![xn−4i]F(x,a−i,b−i,c−i,d−i)\begin{aligned} \sum\limits_{i = 0}^{\min(a, b, c, d, n)} (-1)^{i}f_{n, i, 0}(n-4i)![x^{n-4i}]F(x,a-i,b-i,c-i,d-i) \end{aligned}
总时间复杂度为 O(n2+min⁡(a,b,c,d,n)(ab+cd))O(n^{2} + \min(a, b, c, d, n)(ab + cd))。
</> https://www.luogu.com.cn/record/233698815
CCPC2024 重庆站 D.有限小数 赛时通过【66/278】
也可以从这里查看 https://www.luogu.com/article/cukz766c
时隔将近一年，重新回味这道题，还是惊叹于官方题解及类似题解先看出结论再证明的数学直觉，但是今天我推出了一种不太需要动脑子的推法，比较适合我这种老年人。
先来回顾一下官方题解的结论与证明。令 b=2x5yb′b = 2^{x}5^{y}b'，那么最终答案 dd 一定满足 d=2p5qb′d = 2^{p}5^{q}b'。假设存在一个不含因子 2,52, 5 的大于 11 的正整数 gg，若
  1. g∣bg \mid b 且 g∤dg\nmid d
    • 因为 gcd⁡(a,b)=1\gcd(a, b) = 1 且 g∤dg\nmid d，所以 g∤adg \nmid ad。
    • 又有 g∣bcg \mid bc，所以 ad+bcbd\frac{ad + bc}{bd} 分母中的 gg 约不掉，这就意味这其一定不是有限小数。
  2. g∤bg\nmid b 且 g∣dg \mid d
    • 其实由对称性可以得出结论。
    • 因为 g∣adg \mid ad，并且 ad+bcbd\frac{ad + bc}{bd} 要是有限小数，所以要约掉 gg 一定要满足 g∣bcg \mid bc，但是 g∤bg\nmid b，所以 gcd⁡(g,c)>1\gcd(g, c) > 1，所以 gcd⁡(d,c)>1\gcd(d, c) > 1，不满足 cc 的最小性（把 dd 中除去因子 gg 解依然合法且更优 ）。
这就意味着 g∣bg\mid b 与 g∣dg\mid d 之间是充要的，即 b,db, d 除去因子 2,52, 5 的部分相同。
所以直接 log⁡2\log^{2} 枚举 p,qp, q，然后扩欧求 ad+bc=kadad + bc = kad（其中 c,kc, k 为未知数）的解，对 cc 取最小即可。
接下来我给出自己的推导，会稍微冗长一些，但思路基本没有任何拐弯。
首先约定 b=2x5yb′,d=2p5qd′b = 2^{x}5^{y}b', d = 2^{p}5^{q}d'，则有
ab+cd=12x+p5y+q⋅2p5qad′+2x5yb′cb′d′\begin{aligned} \frac{a}{b} + \frac{c}{d} = \frac{1}{2^{x+p}5^{y + q}}\cdot\frac{2^{p}5^{q}ad'+2^{x}5^{y}b'c}{b'd'} \end{aligned}
要想使其为有限小数，右边的分数的分子必须得把 b′d′b'd' 给约掉，即要存在正整数 k1k_1 满足
2p5qad′+2x5yb′c=k1b′d′2x5yb′c=(k1b′−2p5qa)d′cd′=k1b′−2p5qa2x5yb′\begin{aligned} 2^{p}5^{q}ad' + 2^{x}5^{y}b'c &= k_{1}b'd' \\ 2^{x}5^{y}b'c &= (k_{1}b' - 2^{p}5^{q}a)d' \\ \frac{c}{d'} &= \frac{k_{1}b' - 2^{p}5^{q}a}{2^{x}5^{y}b'} \end{aligned}
因为我们的初始条件约定 d′d' 不能含因子 2,52,5，所以右边分母的 2x5y2^{x}5^{y} 要被约掉，即要存在非负整数 k2k_2 满足
k1b′−2p5qa=k22x5y\begin{aligned} k_{1}b' - 2^{p}5^{q}a = k_{2}2^{x}5^{y} \end{aligned}
使用扩欧解出最小的 k2k_2，因为 b′∣k1b′b' \mid k_{1}b' 且 gcd⁡(2p5qa,b′)=1\gcd(2^{p}5^{q}a, b') = 1，所以 gcd⁡(k2,b′)=1\gcd(k_{2}, b') = 1，即 cd′=k2b′\frac{c}{d'} = \frac{k_{2}}{b'} 不能再化简，故此时 c=k2,d′=b′c = k_{2}, d' = b'，对所有情况的 cc 取最小即可，总时间复杂度 O(Tlog⁡3V)O(T\log^{3}V)，VV 是值域。
其中 d′=b′d' = b' 也印证了官方题解的结论，即合法且互质的解一定满足 bb 和 dd 除去因子 2,52, 5 后剩下的因子相同。
</> https://qoj.ac/submission/1276882
Luogu P5377 [THUPC 2019] 鸽鸽的分割 洛谷难度评级【蓝】
直接算分割成的面有多少个不好算，考虑平面图的欧拉公式 V−E+F=2V - E + F = 2，即 F=E−V+2F = E - V + 2，这个面数还包括了圆之外的一个大平面，所以圆内分割成的面数 F′=E−V+1F' = E - V + 1，现在的问题是怎么计算 EE 和 VV。
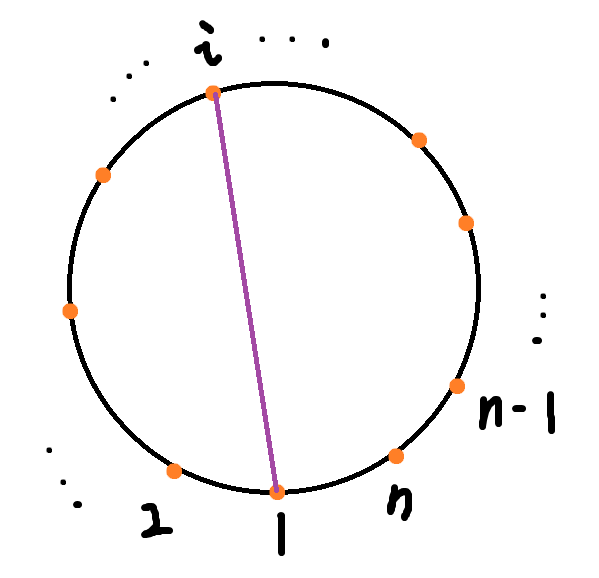
如上图一样给圆上的点编号。
考虑总点数 VnV_n 怎么求。首先在圆上有 nn 个点。对于圆内部的交点，由于交点一定在弦上，我们先枚举所有以 11 为端点的弦，计算出这些弦上的所有交点，然后乘 nn 在除以 44 即可（任意两条弦的交点会被两条弦各统计一次，而任意一条弦上的点会在弦的两个端点处各统计一次）。计算交在弦上的最多的点显然就是左边的点数乘右边的点数，具体公式如下：
Vn=n+n4∑i=3n−1(i−2)(n−i)\begin{aligned} V_{n} = n + \frac{n}{4}\sum\limits_{i = 3}^{n-1}(i - 2)(n - i) \end{aligned}
再考虑 EnE_{n} 怎么求。我们算出了一条弦上的交点数，那这条弦被分成的段数显然就是交点数加 11，也能比较显然地列出式子：
En=n+n2∑i=2n[(i−2)(n−i)+1]\begin{aligned} E_{n} = n + \frac{n}{2}\sum\limits_{i = 2}^{n}[(i - 2)(n - i)+1] \end{aligned}
最终答案 Fn=En−Vn+1F_{n} = E_{n} - V_{n} + 1，把式子推一推化简一下可以 O(1)O(1)。
其实还有一种更简单的推法 Vn=n+(n4),En=n+(n2)+2(n4)V_{n} = n + \binom{n}{4}, E_{n} = n + \binom{n}{2} + 2\binom{n}{4}。
</> https://www.luogu.com.cn/record/234090956

字符串

  • SAM
    1. 字符串 ss 的 SAM 是接受 ss 的所有后缀的最小 DFA。
    2. 记 endpos⁡(t)\operatorname{endpos}(t) 为 tt 在字符串 ss 中所有结束位置的集合，则可以将 ss 的所有子串根据 endpos⁡\operatorname{endpos} 划分成若干个等价类。两个不同的 endpos⁡\operatorname{endpos} 集合要么交集为空集，要么一个被另一个包含。
    3. 令空串的 endpos⁡\operatorname{endpos} 为 {1,2,⋯ ,n}\{1, 2, \cdots, n\}，则每次向这个串的串首添加 Σ\Sigma 中不同的字符并保存，则相当于把 endpos⁡\operatorname{endpos} 做了分裂，这样一直添加下去会形成一个树形结构（这就是后缀树，可以用线段树合并求出每个 endpos⁡\operatorname{endpos} 集合中的具体元素），每个点相当于一个 endpos⁡\operatorname{endpos} 集合，兄弟结点的集合之间没有交集，父亲结点的集合相当于所有儿子结点的集合的并再并上分裂时丢失的位置（分裂时可能会丢失一些位置是因为，这些位置的前缀已经顶到 ss 的头了，没法再串首添加新的字符了）。
    4. 由于分裂到最后，每个叶子结点代表的 endpos⁡\operatorname{endpos} 集合中至少有一个位置，且互不相交，所以叶子结点最多有 nn 个。如果一个父亲只有一个儿子，那这个结点的集合在分裂时一定丢失了一些位置，否则一个父亲至少有两个儿子，所以树的总结点个数小于等于 2n−12n - 1，即只有 O(n)O(n) 种不同的 endpos⁡\operatorname{endpos} 集合（等价类）。
    5. SAM 的每个结点实际就是一个 endpos⁡\operatorname{endpos} 集合，SAM 中的转移边描述的就是如何在一个 endpos⁡\operatorname{endpos} 集合后添加 Σ\Sigma 中的一个字符转移到另外一个 endpos⁡\operatorname{endpos} 集合。
    6. 对于每个结点 uu 代表的 endpos⁡\operatorname{endpos} 集合记录一个 lenulen_u 代表这个集合分出的等价类中最长的串的长度，显然最短的长度就是 lenfau+1len_{fa_u} + 1（注意长度一定是连续的，证明比较显然），如果匹配过程中走到某个 lenu=nlen_u = n 的结点的祖先结点上，就说明一个后缀匹配成功了。
Luogu P4022 [CTSC2012] 熟悉的文章 洛谷难度评级【黑】
其实感觉这题远没有黑题难度，像是各个知识点组合起来把难度拉高了。
首先答案具有单调性，如果存在合法的解满足每一段都大于等于 L+1L + 1，显然这个解的每一段都大于 LL，所以可以二分 L0L_{0}。
接下来就是每一段长度至少为 L0L_{0}，要求合法的总长度。可以套路地进行 dp，设 fif_i 为已经到位置 ii 可以匹配的最长合法长度，显然有
fi=max⁡(fi−1,max⁡j=i−sufii−L0{fj+i−j})\begin{aligned} f_{i} = \max(f_{i - 1}, \max\limits_{j = i - suf_{i}}^{i-L_{0}}\{f_{j} + i - j \}) \end{aligned}
其中 sufisuf_{i} 代表以 ii 为结尾的后缀与原字典的最长匹配长度，这个可以使用 SAM 线性求出。
注意到 i−L0i - L_{0} 和 i−sufii - suf_i 都具有单调性（如果一个串匹配上了，它的子串肯定也能匹配上，所以以 ii 为结尾的后缀向前匹配，至少能匹配到以 i+1i+1 为结尾的后缀向前匹配的位置），然后我们把 fj−jf_j - j 看作一体，那么 dp 的转移就变成了求一个向右滑动的滑动窗口中的最大值，使用优先队列维护即可。
总时间复杂度为 O(∑∣si∣+∑∣ti∣log⁡∣ti∣)O(\sum|s_i| + \sum|t_i|\log|t_i|)。
</> https://www.luogu.com.cn/record/234041180

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...