【模板】manacher 题解

算法介绍

Manacher，是一种用于求解字符串中最长回文串的算法。它可以在

O(n)

的时间里求出以每一个字符为中心的回文串最大长度。

算法流程

下记

p_i

为以第

i

个字符为中心的回文串最大长度。例如，ababa 的长度是 $3$ 。

下面所说的“暴力计算”均指如下代码（假设当前在

i

，需要暴力计算

p_i

）：

CPP

while(s[i+p[i]] == s[i-p[i]]) p[i]++;

首先处理一个问题：有些回文串长度是偶数，有些是奇数。奇数可以枚举中心点；但是偶数不行！为了解决这个问题，我们可以在所有字符之间插入一个 #，这样偶回文串就被我们转换成了奇回文串了。

考虑当前需要求出

p_i

。我们可以记录一个

r

，用来表示在所有

1 \le j < i

的

j

中，以

j

为中心点的回文串的右端点中，最右的那一个。记这个

r

为右端点的回文串的中心点为

j'

。此时我们需要进行分类讨论：

$r>i$

此时我们可以得到下图：

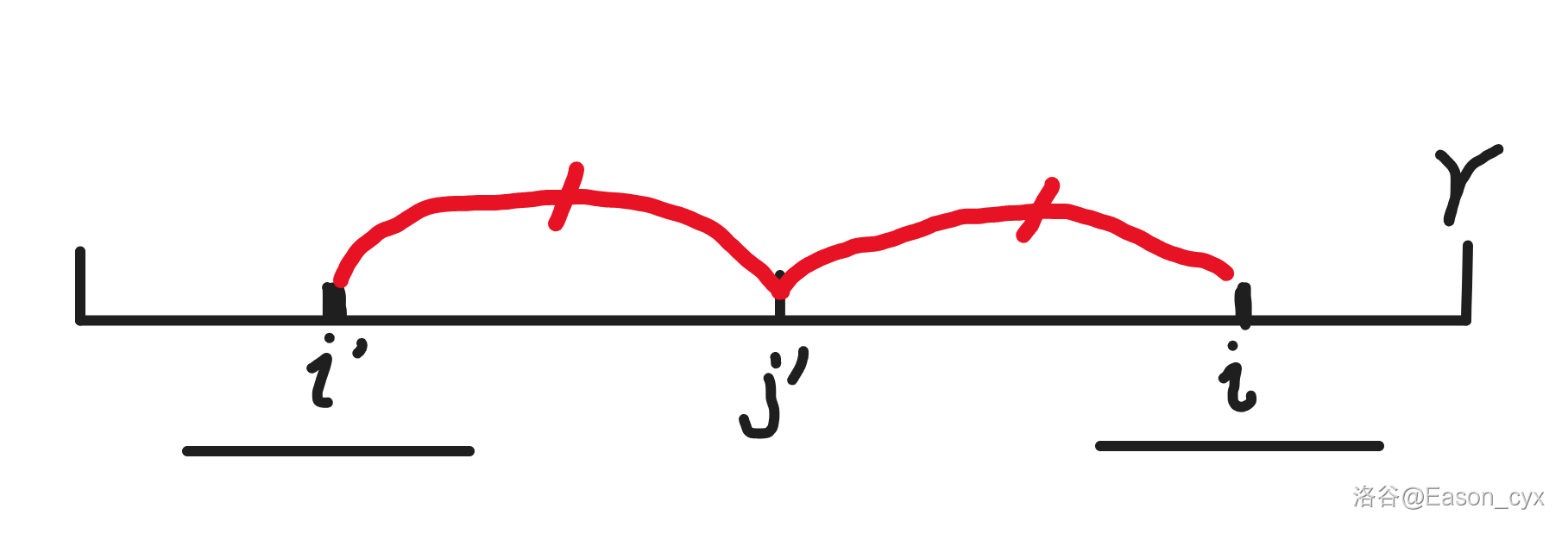
这个图是什么意思？我们首先可以找到

i

以

j'

为对称中心的对称点

i'=j'\times2-i

。然后，因为这一整个是一个回文串，所以对应地，

i'

下面那一段（指那一段子串）和

i

下面那一段一定也相同。所以在这种情况下，

p_i=p_{i'}

，可以直接得出！

但是！情况不一定总是这么好。在

r>i

的情况中，还有另外一种情况：

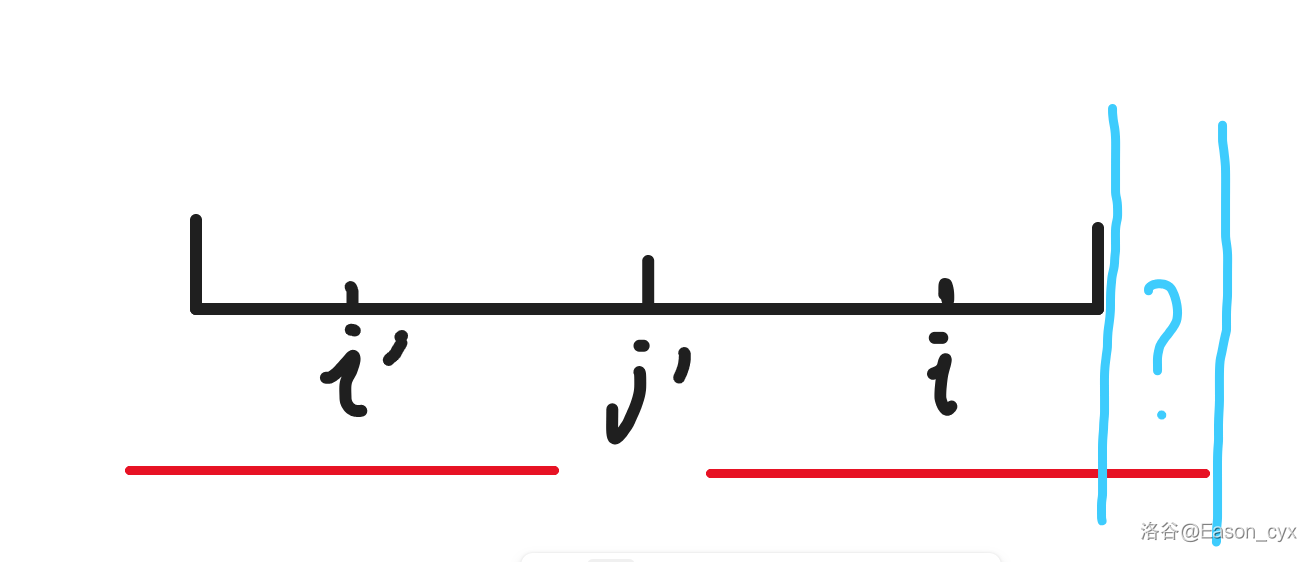
如图，当

p_{i'}

很大的时候，这一段可能超出了整个大回文串，当这个子串对称到以

i

为中心的这边时，右端点超过了

r

，而超出的部分我们一无所知！在这种情况下，我们不能保证

i

的回文长度一定有这么长，只能保证从

i

到

r

这一段一定回文。所以，在这种情况下，我们可以令

p_i=r-i

，然后暴力向外计算

p_i

的最终值。稍后我们会说明这样是对的。

这样，

r>i

的情况暂时被我们解决了。

在每次更新完

p_i

后，注意要实时更新

r

和

j'

，用来计算后面的答案。

$r<i$

此时的情况如图：

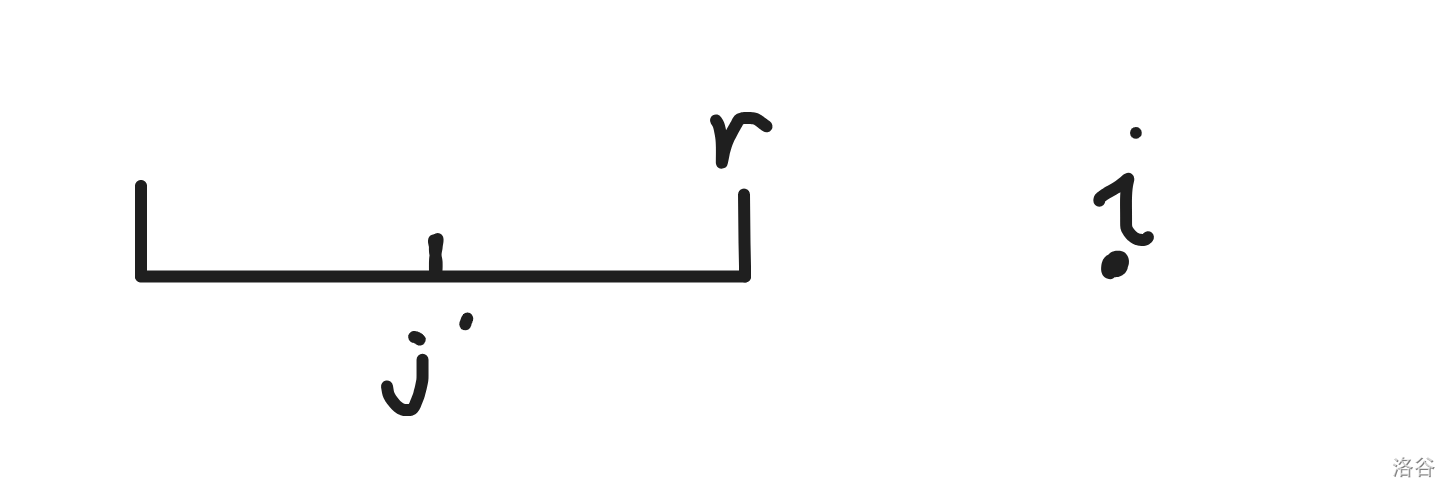
此时可以很清晰地看出，没有任何可以使用的信息，所以只能暴力计算

p_i

了。此时也需要更新

r

。

遍历

1 \sim n

重复如上过程，即可得到所有

p_i

。因为在计算之前在字符串中还插入了一些 #，所以最终答案其实就是

\max p_i-1

。

正确性证明

首先正确性是显然的。

对于复杂度，我们可以感性理解一下：在上面的三种情况中，第一种是

O(1)

的；后两种都在不断地将

r

向后推，而一共只有

n

个位置；所以总的时间复杂度就是

O(n)

。

代码实现

CPP

#include <bits/stdc++.h>
using namespace std;
int p[30000005], mx, id;
//注意：本题数据范围较大，要注意数组大小
//代码中 mx 即为讲解中的 r，id 为讲解中的 j'
int main() {
	string s = "##";
	char c; while(cin >> c) s += c, s += "#";
    //插入 #；为防止越界，在最前面也插一个 #
	int n = s.size(); s = ' ' + s;
	for(int i = 1;i <= n;i++) {
		p[i] = mx > i ? min(p[id*2-i], mx-i) : 1; //三目运算符，分别对应三种情况
		while(s[i + p[i]] == s[i - p[i]]) p[i]++; //暴力计算 p[i]
		if(i + p[i] > mx) mx = i + p[i], id = i; //更新右端点 r
	} int ans = 0; for(int i = 1;i <= n;i++) ans = max(ans, p[i]-1);
	cout << ans << endl;
	return 0;
}

【模板】manacher 题解

文章操作

算法介绍

算法流程

正确性证明

代码实现

相关推荐

评论

【模板】manacher 题解