专栏文章
题解:P13954 [ICPC 2023 Nanjing R] 红黑树
P13954题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @minxdljo
- 此快照首次捕获于
- 2025/12/02 09:54 3 个月前
- 此快照最后确认于
- 2025/12/02 09:54 3 个月前
P13954 红黑树
暴力 DP
设 表示点 为根的子树中的叶子节点到 的路径上黑点个数均为 ,此时的最小修改数。
分两种情况考虑。
第一种,点 的颜色最终为红色,可得转移方程:
第二种,点 的颜色最终为黑色,可得转移方程:
两种情况取 即可。
CPPvoid dfs (int u)
{
if (g[u].size () == 0)
{
f[u][0] = a[u];
f[u][1] = !a[u];
return ;
}
f[u][0] = a[u];
for (int v : g[u]) dfs (v) , f[u][0] += f[v][0];
for (int j = 1;j <= n;j ++)
{
int l1 = 0 , l2 = 0;
for (int v : g[u]) l1 += f[v][j - 1] , l2 += f[v][j];
f[u][j] = min (l1 + !a[u] , l2 + a[u]);
}
}
可以使用 STL 优化以获取更多的分数。
优化
把 看成一个图像 ,可以发现图像是一个凸包(因为最底层的 可以看作一个只有两个点的凸包,而凸包与凸包按位加也会是一个凸包)。设 的图像为 , 的图像为 。如下图所示:
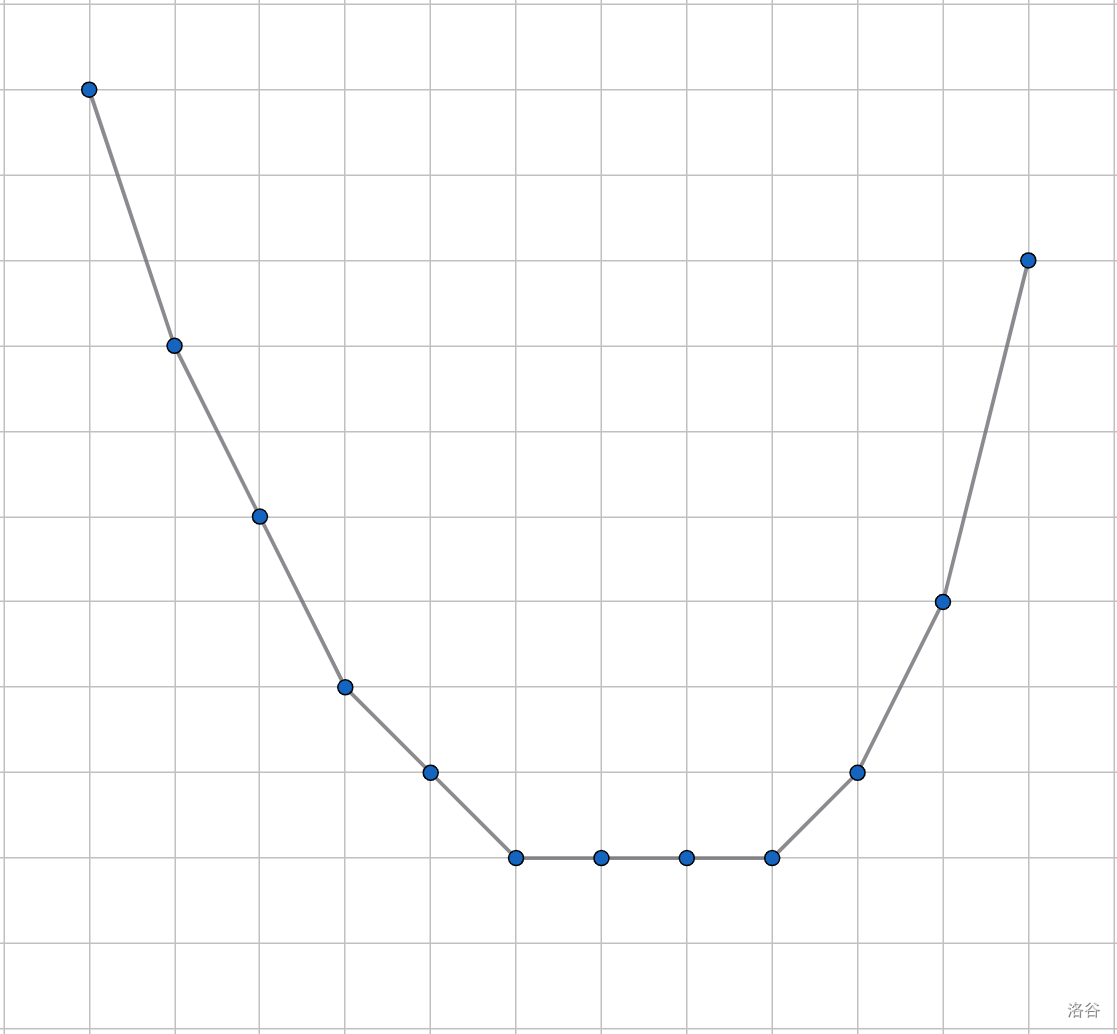
例如这是一个 的图像,那么将其向右移一个单位长度即可变成 的图像,如下:
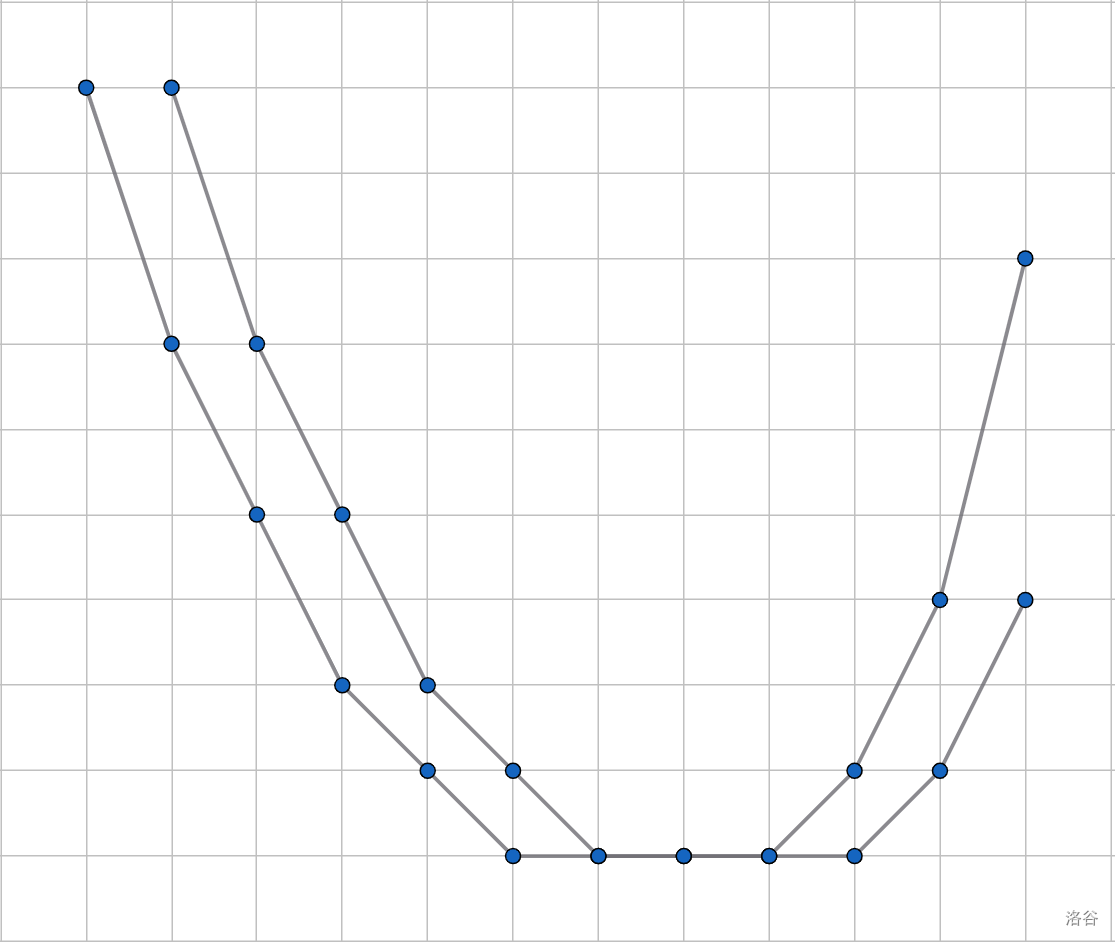
设 斜率为 的一段区间是 。接下来分成两种情况。
此时 的图像会向上一个单位长度,如图:
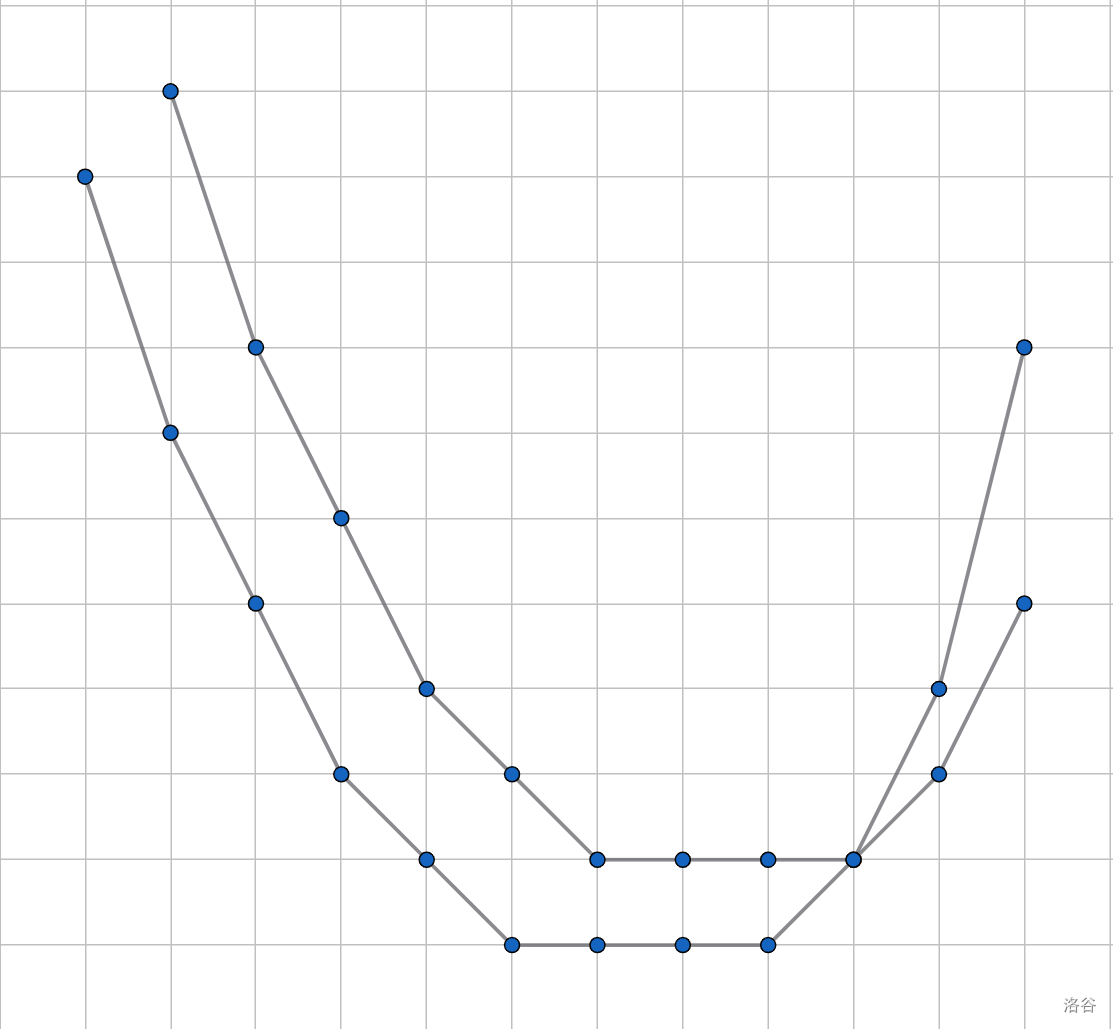
发现当 时 会更小;否则, 更小。而形成的新图像则是 在 的位置插入了一条斜率为 的线段。
此时 的图像会向上一个单位长度,如图:
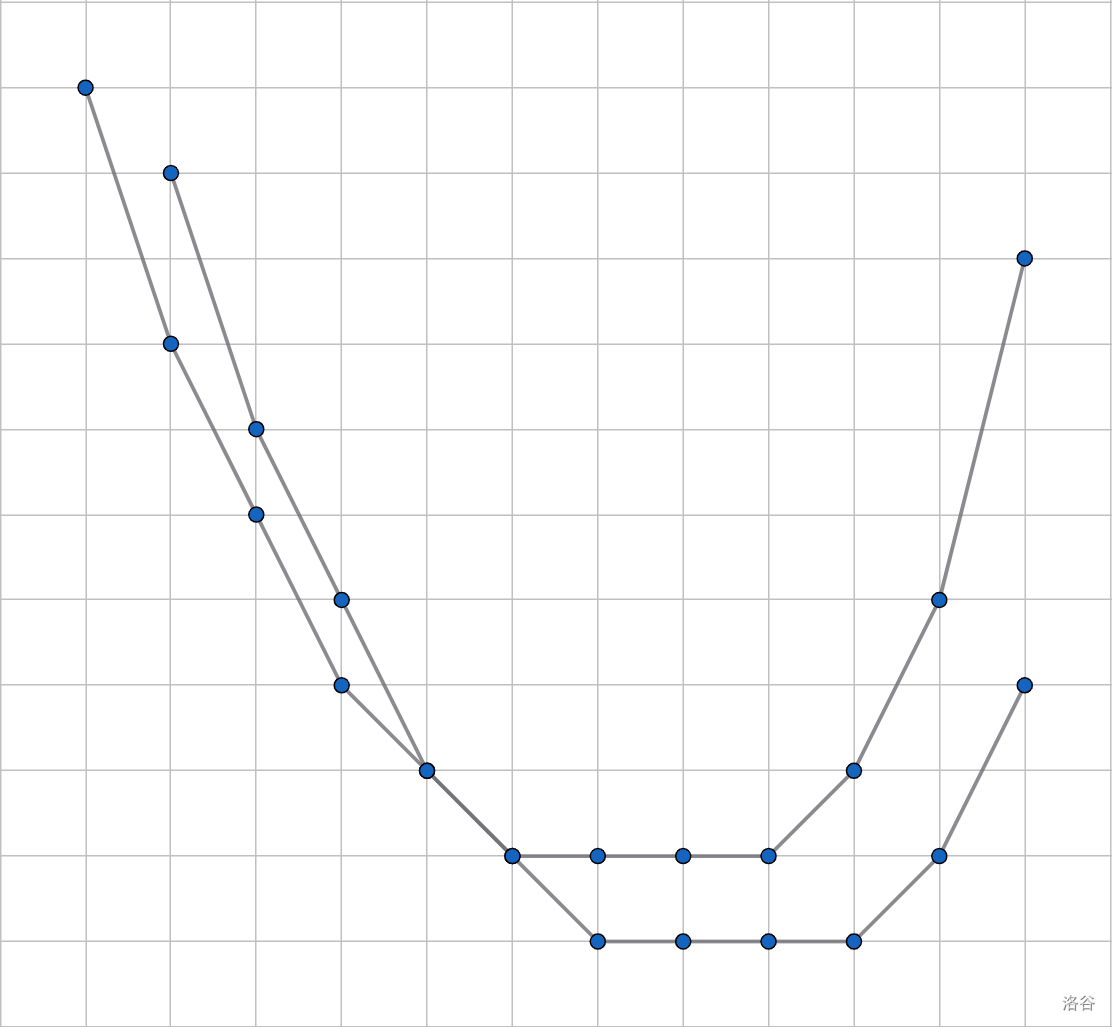
发现当 时 会更小;否则, 更小。而形成的新图像则是 在 的位置添加了一条斜率为 的线段。
那么就使用小根堆存储 对应图像每一位的斜率,在最后插入新线段即可。
可以直接暴力合并,均摊复杂度 。
答案
的值其实就是 子树内的黑点数,用 加上所有负数斜率即为最小值。
AC Code
CPP#include <bits/stdc++.h>
#define int long long
#define fre(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout);
using namespace std;
const int N = 1e5 + 5 , inf = 1e9 + 7;
int n , c[N] , f0[N];
bool a[N];
vector <int> g[N];
priority_queue <int , vector <int> , greater <int> > s[N] , q;
void dfs (int u)
{
f0[u] = a[u] , c[u] = 0;
for (int v : g[u])
{
dfs (v);
f0[u] += f0[v];
if (s[u].empty ()) swap (s[u] , s[v]) , c[u] = c[v];
else
{
while (!q.empty ()) q.pop ();
c[u] = 0;
while (!s[u].empty () && !s[v].empty ())
{
int tmp = s[u].top () + s[v].top ();
q.push (tmp);
if (tmp < 0) c[u] += tmp;
s[u].pop () , s[v].pop ();
}
s[u] = q;
}
}
if (a[u]) s[u].push (-1) , c[u] --;
else s[u].push (1);
}
signed main ()
{
ios::sync_with_stdio(0); cin.tie(0),cout.tie(0);
int T;
cin >> T;
while (T --)
{
cin >> n;
for (int i = 1;i <= n;i ++)
{
char op;
cin >> op;
a[i] = op - 48;
}
for (int i = 2;i <= n;i ++)
{
int p;
cin >> p;
g[p].push_back (i);
}
dfs (1);
for (int i = 1;i <= n;i ++)
{
cout << f0[i] + c[i] << ' ';
g[i].clear ();
while (!s[i].empty ()) s[i].pop ();
}
cout << '\n';
}
return 0;
}
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...