专栏文章

题解：AT_agc012_f [AGC012F] Prefix Median

1123456xwd
AT_agc012_f题解参与者 5已保存评论 4

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
4 条
当前快照
1 份
快照标识符
@mipevxqz
此快照首次捕获于
2025/12/03 10:52
3 个月前
此快照最后确认于
2025/12/03 10:52
3 个月前
查看原文
提供一个官方题解的证明方式（图也源自官方题解）。
dp 本来想也用官方题解的，不过发现 WTimeLlimit的方法和官方题解本质一样，且更加优美，遂学习了这位大佬的。
寻找一个 bb 合法的充要条件，对其计数。
先假设 aa 为一个 1∼2n−11\sim 2n-1 的排列。
必要条件比较好找：
  1. bi∈[i,2n−i]b_{i}\in[i,2n-i]，因为 bib_i 必定右 i−1i-1 个大于和小于他的数。
  2. 不存在 i<ji<j，满足 min⁡(bj,bj+1)<bi<max⁡(bj,bj+1)\min(b_j,b_{j+1})<b_i<\max(b_j,b_{j+1})，因为每次我们的中位数顶多移动一位。
证明其充分性，即我们按照上面的限制可以构造一个序列。
考虑数学归纳法：对于任意正整数 kk，当给他长度为 2k−12k-1 的排列 aa 时，可以构造出一个满足上升要求的 bb。
当 k=1k=1 的时候显然。
设 k=ik=i 时成立，证明 k=i+1k=i+1 的时候成立。此时必定有 bi+1=i+1b_{i+1}=i+1。
而我们可以通过证明对于一个 k=i+1k=i+1 的满足上述限制的 bb，可以通过删除 aa 中的两个数，重标号后，达到一个 k=ik=i 的满足上述限制的 bb，反之可以证明可以由 k=ik=i 推广到 k+1k+1。
而我们只需要证明删除两个数之后，bi∈{i,i+1,i−1}b_{i}\in\{i,i+1,i-1\}，分讨一下：
  1. 当 bi=ib_i = i 时：
    如下图所示，分为 1,2,3,…,i1,2,3,\dots,i 和 i+1,i+2,…,2i−1i+1,i+2,\dots,2i-1 两个组。从后一个组中去除不属于 b1,b2,…,bi−1b_1,b_2,\ldots,b_{i-1} 且最接近 ii 的两个值。
    由于后者的组大小为 i+1i+1，因此一定可以去除。
    此时也一定不会破坏约束条件 2 和 3。
    bi=i+2b_i=i+2 的情况也大致相同。
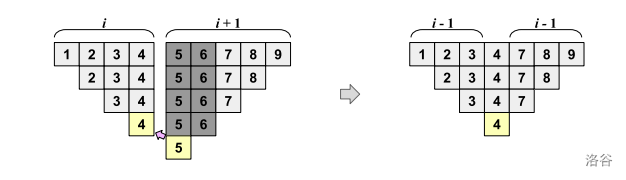
  2. 当 bi=i+1b_i=i+1 时：
    如下图所示，分为 1,2,…,i1,2,\ldots,i 和 i+2,i+3,…,2i−1i+2,i+3,\ldots,2i-1 两个组。
    从两个组中分别去除一个不属于 b1,b2,…,bi−1b_1,b_2,\ldots,b_{i-1} 且最接近 i+1i+1 的一个值。
    由于两个组的大小均为 ii，因此一定可以去除。
    此时也一定不会破坏约束条件 2 和 3。
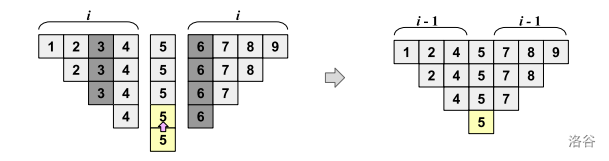
综上，得证。
那么，考虑如何求解呢？
根据上述条件，可以知道 bib_i 的候选值数量比 bi+1b_{i+1} 的多两个，且从后往前选择的时候，bi,bi+1b_i,b_{i+1} 之间的值不能作为候选值，这启发我们从后往前 dp。
设 fi,j,kf_{i,j,k} 表示考虑了 bi∼nb_{i\sim n}，在 [i,2n−i][i,2n-i] 内，有 jj 个合法的候选值 <bi<b_i，kk 个合法的候选值 >bi>b_i。
转移有：
  1. dpi−1,j+1,k+1←dpi,j,kdp_{i-1,j+1,k+1}\gets dp_{i,j,k}，即 bi−1=bib_{i-1}=b_{i} 的情况。
  2. dpi−1,j′,k+2←dpi,j,kdp_{i-1,j',k+2}\gets dp_{i,j,k}，要求满足 j′<j+1j'<j+1，即 bi−1<bib_{i-1}<b_i 的情况，且在这两个之间的候选值都要被干掉。
  3. dpi−1,j+2,k′←dpi,j,kdp_{i-1,j+2,k'}\gets dp_{i,j,k}，要求满足 k′<k+1k'<k+1，即 bi−1>bib_{i-1}>b_i 的情况，且在这两个之间的候选值都要被干掉。
初始值为 dpn,0,0=1dp_{n,0,0}=1，最终答案为 ∑i∑jdp1,i,j\sum_i\sum_j dp_{1,i,j}。
时间为 O(n4)\mathcal{O}(n^4)。
对于 aa 不是排列的时候，我们先排序，然后由值域的扩展了确定是否有那个 +1+1。
C
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define p_b push_back
#define m_p make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define ls k<<1
#define rs k<<1|1
#define mid ((l+r)>>1)
#define gcd __gcd
#define lowbit(x) (x&(-x))
using namespace std;
int rd(){
    int x=0,f=1; char ch=getchar();
    for(;ch<'0'||ch>'9';ch=getchar())if (ch=='-') f=-1;
    for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
    return x*f;
}
void write(int x){
    if(x>9) write(x/10);
    putchar('0'+x%10);
}
const int N=50+5,INF=0x3f3f3f3f,mod=1e9+7;
void add(int &x,int y){
    x+=y;
    if(x>=mod)x-=mod;
}
int dp[N][N<<1][N<<1],a[N<<1],n,ans;
int main(){
    n=rd();
    for(int i=1;i<2*n;i++)a[i]=rd();
    sort(a+1,a+2*n);
    dp[n][0][0]=1;
    for(int i=n;i>=2;i--){
        int x=(a[i-1]!=a[i]),y=(a[2*n-(i-1)]!=a[2*n-i]);
        for(int j=0;j<=2*n;j++){
            for(int k=0;k<=2*n;k++){
                if(!dp[i][j][k])continue;
                add(dp[i-1][j+x][k+y],dp[i][j][k]);
                for(int _j=0;_j<j+x;_j++)add(dp[i-1][_j][k+1+y],dp[i][j][k]);
                for(int _k=0;_k<k+y;_k++)add(dp[i-1][j+1+x][_k],dp[i][j][k]);
            }
        }
    }
    for(int j=0;j<=2*n;j++)for(int k=0;k<=2*n;k++)add(ans,dp[1][j][k]);
    printf("%d\n",ans);
    return 0;
}

评论

共 4 条评论，欢迎与作者交流。

正在加载评论...