前言
本人的国庆假期作业太有意思了,于是就有了这篇文章。
怎么建系
建系其实是把几何问题转化为计算量和代数问题,本文仅讨论平面几何。
首先你需要找到一个适合建系的几何题,这样的题一般有几个特征:
- 纯几何法不太好用。
- 有明显的 90° 角或者可以作垂线。
- 要求线段的长度或者线段的等量关系。
接下来,我会从三个方面和例题讲解如何使用好建系。
从线开始
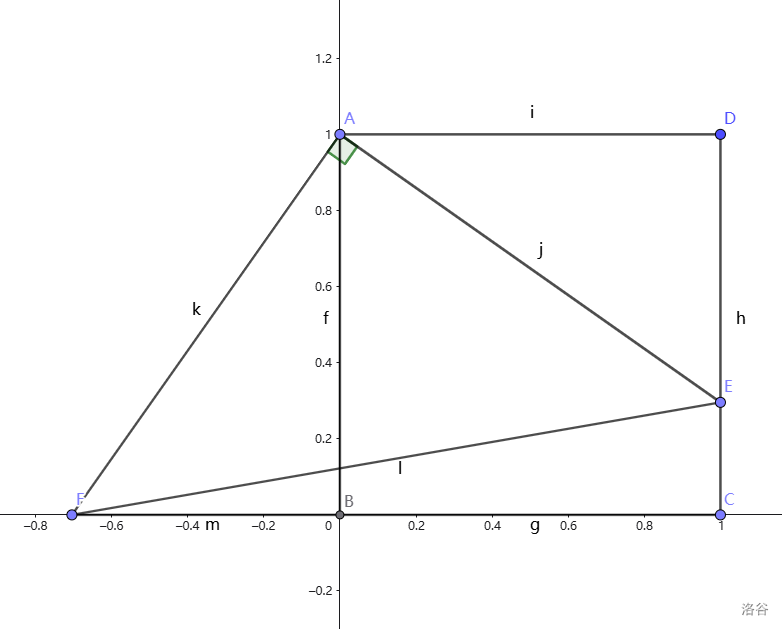
国庆作业 3 T14(节选):
如图,E 是正方形
ABCD 的边
CD 上一点,把
△ADE 旋转到
△ABF 的位置。求证
△AEF 是等腰直角三角形。
其实这题用纯几何法会快一点,这里使用建系仅作为示例。
解法
建立如图所示的平面直角坐标系:
因为旋转,所以
AF=AE ,即
△AEF 是等腰三角形。
由于题面并未给出正方形
ABCD 的边长,不妨设为
1 ,可以得到:
因为
E 点是动点,因此把它设为
E(1,k)。
所以:
FB=ED=1−k,即:
F(k−1,0)然后解出直线
AF 和
AE 的解析式:
又因为
1−k1×(k−1)=−1 ,所以直线
AF 和
AE 的斜率相乘为
−1 ,即:
AF⊥AE 。
所以
△AEF 是等腰直角三角形。
构造直角
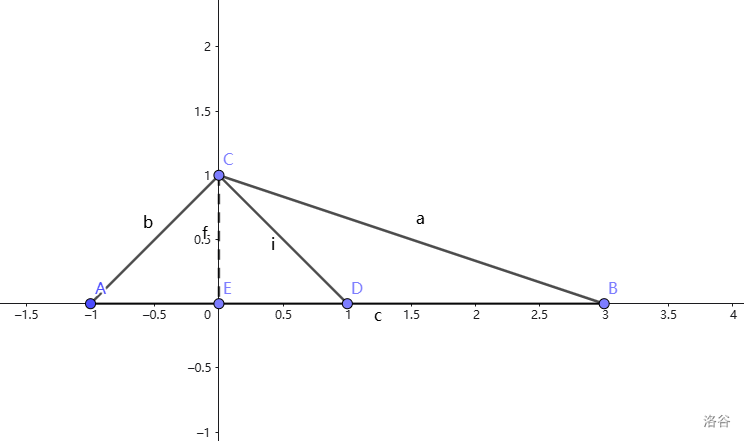
这是昆明市盘龙区
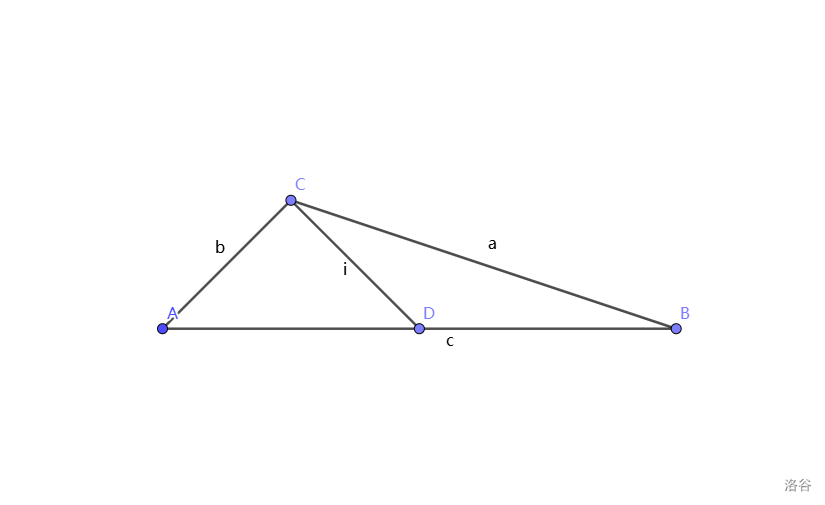
2024∼2025 下学期初二数学期末考 T26(2)。
如图,在
△ABC 中,
BC=a ,
AC=b ,
AB=c ,
CD 是
AB 边的中线,在
△ABC 中,用
a,b,c 表示
CD2
以下是本人在考场上的解法:
解法
作
CE⊥AB ,再建立如图所示的平面直角坐标系:
不妨设
CE 长为
1 ,可以得到:
C(0,1) ;
设
A(m,0) ,
B(n,0),则
D(2m+n,0) 用勾股定理得:
所以:
CD2=(2m+n)2+1=4n2+m2+2mn+1=4c2+4mn+1又因为:
n2+m2=a2+b2−2所以:
c2=a2+b2−2mn−2即:
2mn=a2+b2−c2−2代入可得:
CD2=4c2+4mn+1=4c2+2a2+2b2−2c2−4+1=42a2+2b2−c2所以答案就是:
CD2=42a2+2b2−c2处理等角
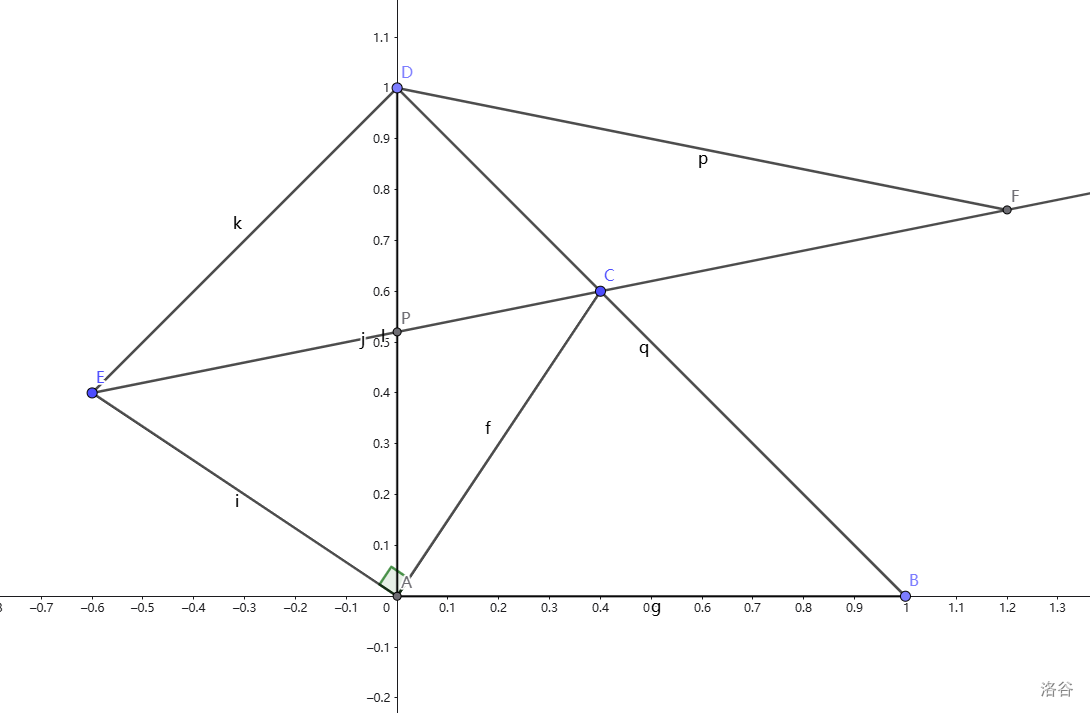
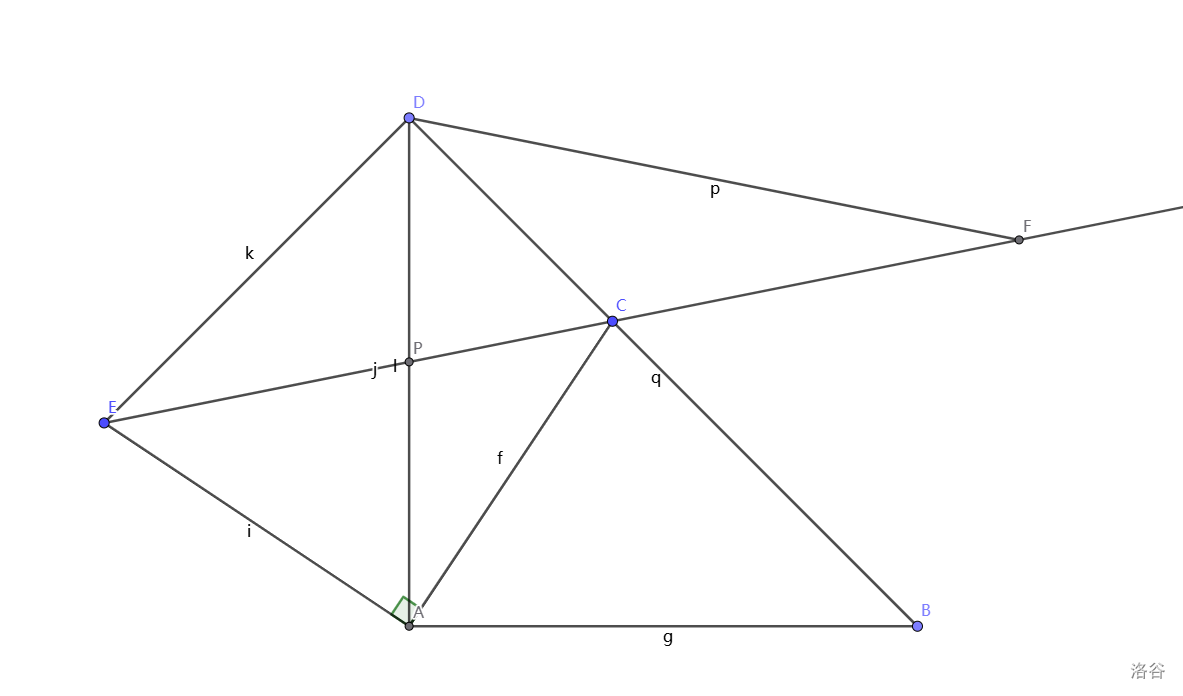
国庆作业 3 T21(2):
如图
△ADE 由
△ABC 绕点
A 逆时针旋转
90° 得到,且
B 的对应点
D 恰好落在
BC 的延长线上,
AD 与
EC 相交于点
P , 点
F 是
EC 延长线上一点,且
∠CDF=∠DAC ,求
DF 与
PF 的数量关系。
我不会纯代数证明啊。
解法
建立如图所示的平面直角坐标系,不妨设
AB=1 ,易得:
所以:
BD:y=−x+1因为
C 在
BD 上,设
C(k,−k+1) ,不难得到:
E(k−1,k)所以:
EF:y=(−2k+1)x+2k2−2k+1然后似乎就难以为继了,但是我们还有一个条件
∠CDF=∠DAC 没用,考虑三角函数。
不难得到:
tan∠CDF=−k+1k再求出直线
DF 的斜率(也就是和
x 轴夹角的
tan 值,记为
m),使用和角公式:
所以:
DF:y=(2k−1)x+1 联立,求个交点:
F(2k−1k2−k,k2−k+1)P(0,2k2−2k+1)再用勾股定理:
DF2=(2k−1k2−k)2+(k2−k)2PF2=(2k−1k2−k)2+(k2−k−2k2+2k)2=(2k−1k2−k)2+(k2−k)2所以:
DF2=PF2
所以:
DF=PF得证。
总结
建系其实是几何题的通用解法,但是这通常伴随着巨大的计算量。
因此在几何题里尽量少用建系,不然你会发现你渐渐的忘记纯代数证法了(别问我怎么知道的!)
引用一位教练的名言做总结吧:
有些人把高级的数据结构学傻了,连差分这种东西都要拿线段树写。