2025.11.6

T1：

如果最大的

a_i

去干其他的

b_i

还有剩余，显然需要加上这些多余的，最大的

b_i

亦然，所以 st 表即可。

CPP

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 2e5 + 5;

int n, q, s1[N], s2[N], Log2[N];

signed a[N], b[N];

pair <signed, signed> st1[N][21], st2[N][21];

pair <signed, signed> query1 (int l, int r) {
	int s = Log2[r - l + 1];
	return max(st1[l][s], st1[r - (1 << s) + 1][s]);
}

pair <signed, signed> query2 (int l, int r) {
	int s = Log2[r - l + 1];
	return max(st2[l][s], st2[r - (1 << s) + 1][s]);
}

signed main() {
//	system("fc max.out ans.out");
	freopen("max.in","r",stdin);
	freopen("max.out","w",stdout);
	for (int i = 2; i <= 2e5; ++ i ) Log2[i] = Log2[i >> 1] + 1;
	scanf("%lld%lld", &n, &q);
	for (int i = 1; i <= n; ++ i ) scanf("%d", a + i), s1[i] = s1[i - 1] + a[i], st1[i][0] = {a[i], i};
	for (int i = 1; i <= n; ++ i ) scanf("%d", b + i), s2[i] = s2[i - 1] + b[i], st2[i][0] = {b[i], i};
	for (signed j = 1; j <= 17; ++ j )
	    for (signed i = 1; i + (1 << (j - 1)) - 1 <= n; ++ i )
	        st1[i][j] = max(st1[i][j - 1], st1[i + (1 << (j - 1))][j - 1]),
	        st2[i][j] = max(st2[i][j - 1], st2[i + (1 << (j - 1))][j - 1]);
	    
	while (q -- ) {
		signed l1, r1, l2, r2;
		scanf("%d%d%d%d", &l1, &r1, &l2, &r2); 
		int S1 = s1[r1] - s1[l1 - 1], S2 = s2[r2] - s2[l2 - 1];
        int id1 = query1 (l1, r1).second, id2 = query2 (l2, r2).second;
        int maxn = max(a[id1] + b[id1 + l2 - l1], a[id2 - (l2 - l1)] + b[id2]);
		printf("%lld\n", max(0ll, maxn - max(S1, S2)) + max(S1, S2));
	}
	return 0;
}

T2：

不用管题目中的

f

定义，它就是

C_i^x

。

对于

k

大的情况，暴力算即可。

对于

k

小的情况，考虑递推预处理。

设

f_{x,r}

表示

\sum_{i=0}^n{[i\mod k=r]C_i^x}

。

然后我们画个图（杨辉三角）。

首先我们知道

C_n^m=C_{n-1}^{m-1}+C_{n-1}^{m}

因此：

\sum_{i=0}^n{[i\mod k=r]C_i^x}=\sum_{i=0}^n{[i\mod k=r](C_{i-1}^{x-1}+C_{i-1}^x)}

=\sum_{i=0}^n{[i\mod k=r]C_{i-1}^{x-1}}+\sum_{i=0}^n{[i\mod k=r]C_{i-1}^x}

=\sum_{i=0}^n{[i\mod k=r-1]C_{i}^{x-1}}+\sum_{i=0}^n{[i\mod k=r-1]C_{i}^x}

=f_{x-1,r-1}+f_{x,r-1}

即如图：

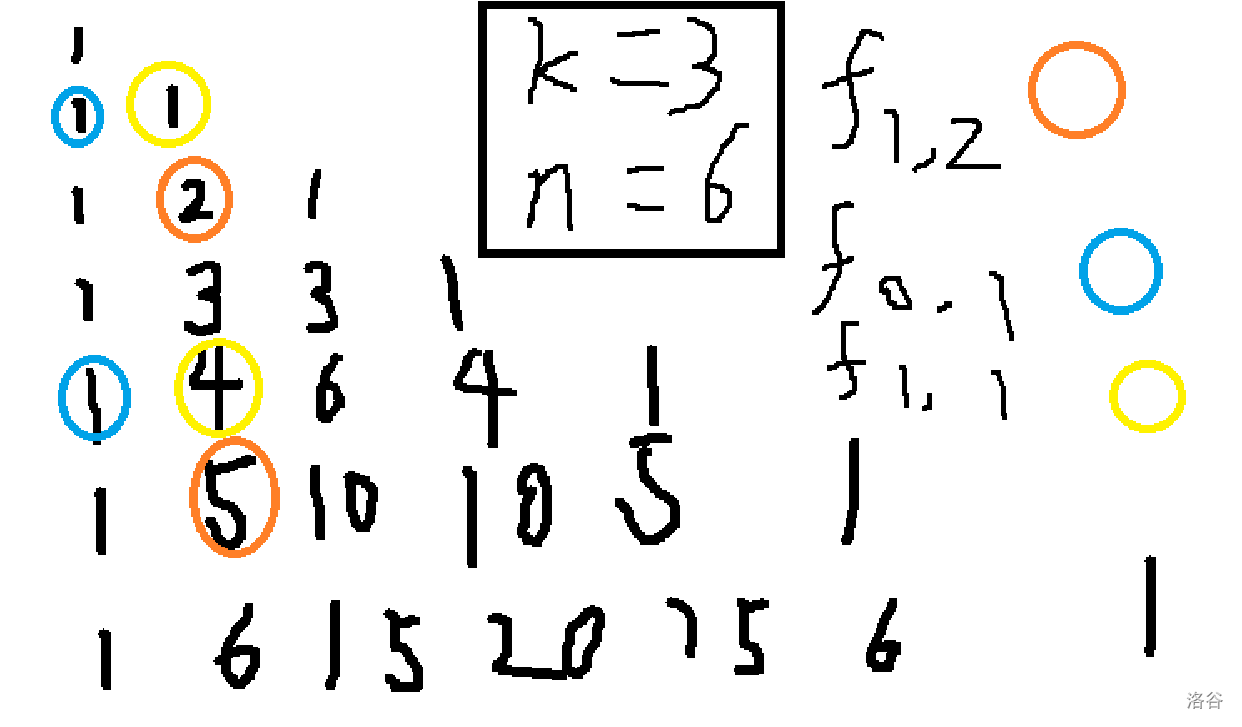
然后你发现你不知道如何得到

f_{x,0}

，暴力算显然不可行。

考虑设它为

Q

。

f_{x,0}=Q

f_{x,1}=f_{x-1,0}+f_{x,0}=f_{x-1,0}+Q

f_{x,2}=f_{x-1,1}+f_{x,1}=f_{x-1,1}+f_{x-1,0}+Q

......

然后你就能推出

f_{x,r}=Q+b

考虑计算所有项的和，显然为

\sum_{i=0}^nC_i^x

经典结论，这个东西等于

C_{n+1}^{x+1}

\sum b

可以轻松推得，显然加起来一共有

k

个

Q

，然后

Q=\frac{C_{n+1}^{x+1}-\sum b}{k}

。

然后你发现假了，因为

k|n

，

f_{x,0}

包含

C_{n}^x

，但是其他的任何

f_{x,r}

不包含

C_n^x

。

如图：

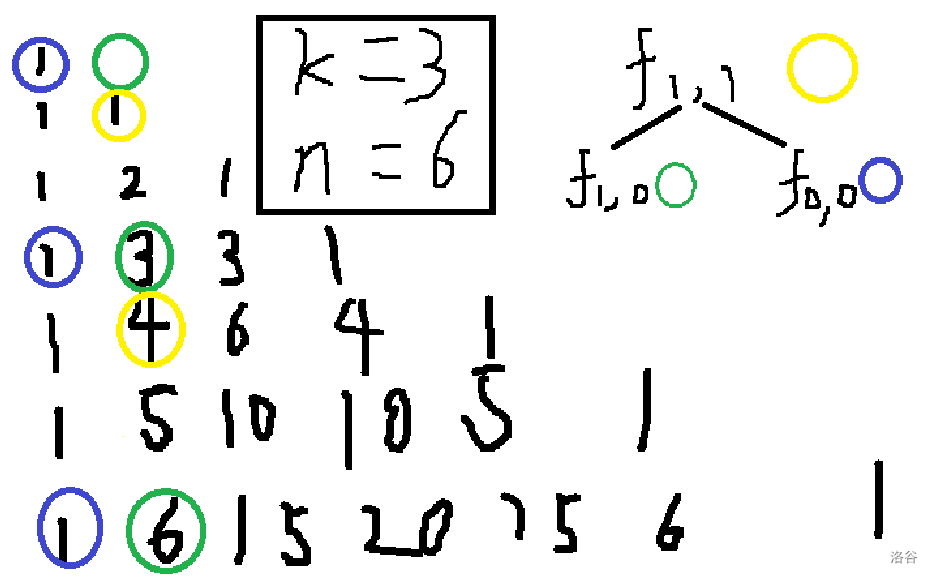
对于黄点而言，最底下的蓝点和绿点不应给它贡献。

所以我们将前面所有式子的

\sum_{i=0}^n

改为

\sum_{i=0}^{n-1}

，先忽略掉

C_n^x

，最后特判

r=0

的情况下加上

C_n^x

即可。

时间复杂度

O(n\sqrt n)

CPP

#include <bits/stdc++.h>

#define int long long 

using namespace std;

const int N = 1e5 + 1, mod = 1e9 + 7;

int ksm (int a, int n) {
	int ans = 1;
	while (n) {
		if (n & 1) ans = ans * a % mod;
		a = a * a % mod;
		n >>= 1;
	}
	return ans;
}

int n, k, q, jc[N], inv[N], f[N][201];

int C (int n, int m) {
	if (n < 0 || m < 0 || m > n) return 0;
	return jc[n] * inv[m] % mod * inv[n - m] % mod;
}

signed main() {
	freopen("sum.in","r",stdin);
	freopen("sum.out","w",stdout);
	jc[0] = 1;
	for (int i = 1; i < N; ++ i ) jc[i] = jc[i - 1] * i % mod;
	inv[N - 1] = ksm (jc[N - 1], mod - 2);
	for (int i = N - 2; i >= 0; -- i ) inv[i] = inv[i + 1] * (i + 1) % mod;
	scanf("%lld%lld%lld", &n, &k, &q);
	if (k <= 200) {
		f[0][0] = n / k;
		for (int r = 1; r < k; ++ r ) f[0][r] = n / k;
		for (int x = 1; x <= n; ++ x ) {
			int sum = 0;
			for (int r = 1; r < k; ++ r ) f[x][r] = (f[x - 1][r - 1] + f[x][r - 1]) % mod, (sum += f[x][r]) %= mod; 
			int Q = (C (n, x + 1) - sum + mod) * ksm (k, mod - 2) % mod;
			for (int r = 0; r < k; ++ r ) (f[x][r] += Q) %= mod;
		}
	}
	while (q -- ) {
		int x, r;
		scanf("%lld%lld", &x, &r);
		if (k == 1) {
			printf("%lld\n", C (n + 1, x + 1));
		} else if (k > 200) {
			int ans = 0;
			for (int i = r; i <= n; i += k ) (ans += C (i, x)) %= mod;
			printf("%lld\n", ans);
		} else {
			printf("%lld\n", (f[x][r] + C (n, x) * (r == 0)) % mod);
		}
	}
	return 0;
}

T3：

这是经典缺一分治，首先我们知道 Flogd 支持每次加入一个点

O(n^2)

更新每个点的答案，所以我们分治，每次将这个区间前半部分的点加入，递归右半区间，然后撤销这些操作，加入右边所有点，递归左半区间，当区间长度为

1

的时候更新答案，时间复杂度

O(n^3\log n)

。

CPP

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 1e6 + 5, INF = 1e18;

int n, q, a[305][305], ans[N], f[11][305][305];

struct node {
	int s, t, id;
};

vector <node> g[305];

inline void solve (const signed l, const signed r, const signed d) {
	if (l == r) {
		for (node i : g[l]) ans[i.id] = f[d][i.s][i.t];    
		return;
	}
	signed mid = (l + r) >> 1;
	for (signed i = 1; i <= n; ++ i )
	    for (signed j = 1; j <= n; ++ j )
	        f[d + 1][i][j] = f[d][i][j];
	        
	for (signed k = l; k <= mid; ++ k )
	    for (signed i = 1; i <= n; ++ i )
	        for (signed j = 1; j <= n; ++ j )
	            f[d + 1][i][j] = min(f[d + 1][i][j], f[d + 1][i][k] + f[d + 1][k][j]);
	            
	solve (mid + 1, r, d + 1);
	for (signed i = 1; i <= n; ++ i )
	    for (signed j = 1; j <= n; ++ j )
	        f[d + 1][i][j] = f[d][i][j];
	        
	for (signed k = mid + 1; k <= r; ++ k )
	    for (signed i = 1; i <= n; ++ i )
	        for (signed j = 1; j <= n; ++ j )
	            f[d + 1][i][j] = min(f[d + 1][i][j], f[d + 1][i][k] + f[d + 1][k][j]);
	            
	solve (l, mid, d + 1);
	return; 
}

int read() {
	int x = 0;
	char c = getchar();
	while (c < '0' || c > '9') c = getchar();
	while (c >= '0' && c <= '9') {
		x = x * 10 + c - '0';
		c = getchar();
	} 
	return x;
}

signed main() {
//	system("fc distance.out asd.out");
	freopen("distance.in","r",stdin);
	freopen("distance.out","w",stdout);
	n = read(), q = read();
	for (int i = 1; i <= n; ++ i )
	    for (int j = 1; j <= n; ++ j )
	        a[i][j] = read(), f[0][i][j] = a[i][j];
	
	for (int i = 1; i <= q; ++ i ) {
		int s, t, p;
		s = read(), t = read(), p = read();
		g[p].push_back({s, t, i});
	}
	solve (1, n, 0);
	for (int i = 1; i <= q; ++ i ) printf("%lld\n", ans[i]);
	return 0;
}

文章操作

相关推荐

评论

2025.11.6