2020 CCPC Weihai J. Steins;Game 题解

题意：有一个博弈问题：有 $n$ 堆石子，每一堆有黑白之中的一种颜色。Alice 和 Bob 轮流取，每次可以选择任意一堆白色石子或者个数最少的一堆黑色石子，从中取若干个石子。取完的人获胜。

现在 Bob 要给每一堆石子染色，问他赢的染色方案数。

首先是博弈论问题，考虑算出一个状态的 SG 值。白色石子显然构成一个 nim 游戏。对于黑色石子可以打表，设最少的一堆黑色石子个数为 $m$，$m$ 的出现次数为 $c_m$，打表可得它的 SG 值是 $m-((c_m-\text{[all the black piles have same size]})\bmod 2)$。

接下来开始计数。枚举黑色石子的最小值 $m$ 和 $c_m$。先钦定不会出现所有黑色石子全部大小相等的情况，那么就可以算出白色石子的 SG 值。而大小不超过 $m$ 的石子已经全部确定了，于是问题就可以转化为在大小 $>m$ 的堆中选一个子集使得异或和等于给定值。

我并不会做这个计数，所以我使用了特殊工具。

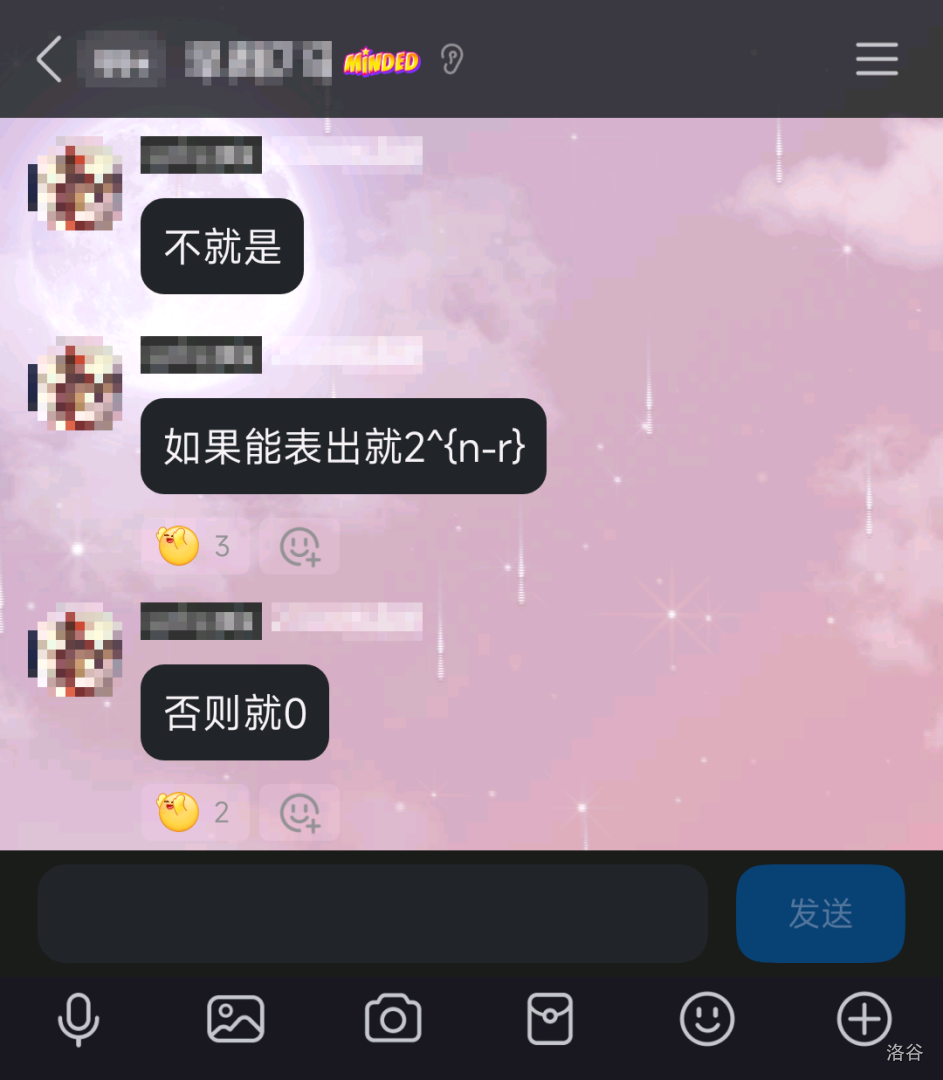
其原因是：选择所有未成功插入线性基的集合的任意一个子集，都恰好存在一个成功插入线性基的集合里的一个子集与之匹配。

然后特判一下所有黑色石子全部大小相等的情况。时间复杂度 $O(n\log n+n\log V)$。