专栏文章

题解：P5656 【模板】二元一次不定方程 (exgcd)

__Weslie_
P5656题解参与者 6已保存评论 6

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
6 条
当前快照
1 份
快照标识符
@minkzc9d
此快照首次捕获于
2025/12/02 04:07
3 个月前
此快照最后确认于
2025/12/02 04:07
3 个月前
查看原文
这是有必要的。因为我 CSP-S 考前两个周还不会 exgcd。
upd 10.27 修锅。
前置知识
  • gcd⁡(x,y)\gcd(x,y) 是指 x,yx,y 的最大公约数，具体来说是最大的正整数 pp 使得 x mod p=0x\bmod p=0，y mod p=0y\bmod p=0。
  • 特别地，我们规定 gcd⁡(x,0)=x\gcd(x,0)=x。
exgcd，全称扩展欧几里得算法（Extended Euclidean algorithm, EXGCD），常用于求 ax+by=gcd⁡(a,b)ax+by=\gcd(a,b) 的一组可行解。

算法过程

它与 gcd 是类似的。
回顾一下普通 gcd 的过程：
如果你不知道欧几里得算法（gcd）
欧几里得算法（gcd）可以在 O⁡(log⁡V)\operatorname{O}(\log V) 的时间复杂度内求出两个数的最大公约数。
它的过程是这样的：
  • 假设当前要求 gcd⁡(a,b)\gcd(a,b)。
  • 如果 b=0b=0，那么 gcd⁡(a,0)=a\gcd(a,0)=a（人为规定的），于是返回。
  • 否则，递归求解 gcd⁡(b,a mod b)\gcd(b,a\bmod b) 的值，并返回。
在这一过程中，我们用到了一个定理 gcd⁡(a,b)=gcd⁡(b,a mod b)\gcd(a,b)=\gcd(b,a\bmod b)。证明在 OI Wiki 上有。
那么它的复杂度为何是 O⁡(log⁡n)\operatorname{O}(\log n) 的呢？
gcd 为何是 O⁡(log⁡n)\operatorname{O}(\log n) 的
先看 log⁡\log 底数：它是 22。
我们考虑当前的 gcd⁡(a,b)\gcd(a,b)。
那么接下来它会有以下两种情况：
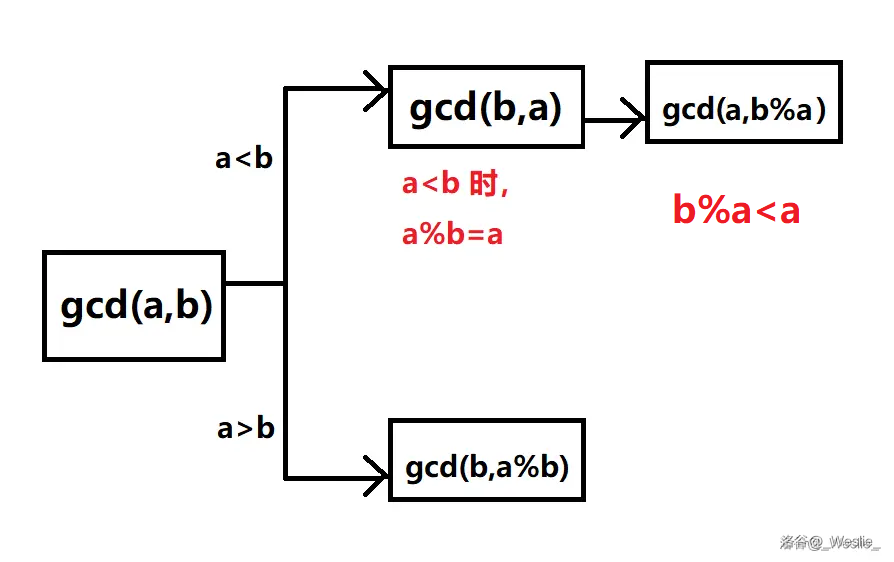
每次走上面的情况时，下一次都一定会走下面的情况，而 2×(a mod b)≤a2\times (a\bmod b)\le a，所以复杂度是 O⁡(log⁡V)\operatorname{O}(\log V) 的。
为何 2×(a mod b)≤a2\times (a\bmod b)\le a？
考虑令 b=⌊a2⌋+1b=\lfloor\dfrac{a}{2}\rfloor+1，则 a mod b=⌊a2⌋−1a\bmod b=\lfloor\dfrac{a}{2}\rfloor-1（aa 为偶数）或 ⌊a2⌋\lfloor\dfrac{a}{2}\rfloor（aa 为奇数）。
如果 bb 更大，那么 a mod b=a−ba\bmod b=a-b 更小。
如果 bb 更小，可以证明 a mod b≤b≤a2a\bmod b\le b\le \dfrac{a}{2}。
那么我们如果要求 ax+by=gcd⁡(a,b)ax+by=\gcd(a,b) 的解，是否可以先求出 bx+(a mod b)y=gcd⁡(b,a mod b)bx+(a\bmod b)y=\gcd(b,a\bmod b) 的解？
是可以的。假设下面方程的一组解是 x0,y0x_0,y_0，则上面方程的解如下：
x=y_0\\ y=x_0-\lfloor\dfrac{a}{b}\rfloor \times y_0 \end{cases}$$ ::::success[证明] 考虑设 $a=kb+c$，容易注意到： $$\begin{cases} k=\lfloor\dfrac{a}{b}\rfloor\\ c=a\bmod b=a-\lfloor\dfrac{a}{b}\rfloor\times b \end{cases}$$
\begin{aligned} \gcd(a,b)&=bx_0+cy_0 \&=bx_0+(a-\lfloor\dfrac{a}{b}\rfloor\times b)y_0 \&=bx_0+ay_0-\lfloor\dfrac{a}{b}\rfloor\times b\times y_0 \&=ay_0+b(x_0-\lfloor\dfrac{a}{b}\rfloor\times b\times y_0) \end{aligned}
证毕。 :::: 但是我们不能无限制的递归下去。我们需要找寻一个边界条件。它就是 $b=0$ 的时候，这时我们直接返回 $$\begin{cases} x=1\\ y=0 \end{cases}$$ 即可。 证明：显而易见的。直接把它代入原方程。 ::::success[一个简单的 exgcd 代码实现] ``` #define ll long long ll x,y; void exgcd(ll a,ll b){ if(b==0){ x=1; y=0; return; } exgcd(b,a%b); ll t=x; x=y; y=t-a/b*y; } ``` 你还可能见到另外一种写法。 ``` void exgcd(ll &x,ll &y,ll a,ll b){ if(b==0){ x=1; y=0; return; } exgcd(x,y,b,a%b); ll t=x; x=y; y=t-a/b*y; } ``` 这里面的 `&` 是取地址符，具体来说，当你递归调用时，如果内层的 $x,y$ 被改变了，它会连带着外层的 $x,y$ 一起改变。 :::: ## 例题 1 例题 $1$：[P1082 [NOIP 2012 提高组] 同余方程](https://www.luogu.com.cn/problem/P1082) 求关于 $x$ 的同余方程 $ a x \equiv 1 \pmod {b}$ 的最小正整数解。 对于 $100\%$ 的数据，$2 ≤a, b≤ 2,000,000,000$。 ::::success[Solution] 正常我们解决 exgcd 问题都需要 $a,b$ 两个常量，但是这题只有 $1$ 个。 没关系！我们只需要把方程转化为 $ax+by\equiv 1(\pmod b)$ 即可。 由于 $by\equiv 0$，所以 $y$ 是多少对答案并不重要。 但是 exgcd 解出来的只是一组解，所以我们要把解出来的 $x_0$ 对 $b$ 取模来求解。 因为 $x_0$ 有可能是负数，所以应该先让 $x\leftarrow x_0\bmod b$，然后再让 $x\leftarrow x+b$。但是若是 $x_0$ 初始就是整数，这样会让 $x+b$ 不是最小正答案，所以还需要让 $x\leftarrow x\bmod b$。 :::success[Code] ``` #include<iostream> #include<cstdio> #define ll long long using namespace std; ll x,y; void exgcd(ll a,ll b){ if(b==0){ x=1; y=0; return; } exgcd(b,a%b); ll t=x; x=y; y=t-a/b*y; } int main(){ ll a,b; cin>>a>>b; exgcd(a,b); x=(x%b+b)%b; cout<<x; return 0; } ``` ::: :::: ## 变式 1 变式 $1$：[P2613 【模板】有理数取余](https://www.luogu.com.cn/problem/P2613) 求 $bx\equiv a\pmod {19260817}$ 的解。 ::::success[Solution] 如果我们求出 $bx\equiv 1\pmod {19260817}$ 的根 $x_0$，那么 $ax_0$ 就是符合条件的 $x$ 之一。 :::error[为什么 $ax_0$ 是符合条件的 $x$ 之一！] 因为 $bx_0\equiv 1$，那么 $abx_0\equiv a$。 ::: 把上面的代码改一改就能过。 :::: 事实上，这个变式的意义是可以通过 exgcd 来求任意一个整数的逆元，相比起费马小定理与快速幂的组合，适用范围更广。 ## 例题 2 例题 $2$：[P5656 【模板】二元一次不定方程 (exgcd)](https://www.luogu.com.cn/problem/P5656) ~~exgcd 基础，【模板】exgcd 就不基础。~~ 对于普通的 exgcd，它有非常多的不同。 ### 裴蜀定理的应用 正常的 exgcd 是解 $ax+by=\gcd(a,b)$，但是 P5656 是解 $ax+by=c$！ 别怕，我们假设 $ax+by=\gcd(a,b)$ 已经解出来了 $x_0,y_0$。 那么 $ax+by=c$ 的解会是多少呢？ 不难发现 $a\dfrac{x_0c}{\gcd(a,b)}+b\dfrac{y_0c}{\gcd(a,b)}=c$。 所以我们需要保证 $\dfrac{x_0c}{\gcd(a,b)}$ 和 $\dfrac{y_0c}{\gcd(a,b)}$，也就是 $c\bmod \gcd(a,b)=0$。 如果不等于零，可以直接判断没有整数解。 :::info[为何“如果不等于零，可以直接判断没有整数解”？] 这就是裴蜀定理。[P4549 题解区](https://www.luogu.com.cn/problem/solution/P4549)有关于这个的证明。 ::: 但是现在我们要求它的正整数解的数量，所有正整数解中 $x$ 的最小值，所有正整数解中 $y$ 的最小值，所有正整数解中 $x$ 的最大值，以及所有正整数解中 $y$ 的最大值，或所有整数解中 $x$ 的最小正整数值，$y$ 的最小正整数值。 我们发现这个东西显然是不可能用普通的 exgcd 做了。假设我们现在已经通过 exgcd + 裴蜀定理解决了 $ax+by=c$ 的一组特殊解，那么我们该如何求出它的正整数解的数量，所有正整数解中 $x$ 的最小值，所有正整数解中 $y$ 的最小值，所有正整数解中 $x$ 的最大值，以及所有正整数解中 $y$ 的最大值，或所有整数解中 $x$ 的最小正整数值，$y$ 的最小正整数值呢？ ### 基础：单推多 这个是以下推导的基础。 首先，我们设一组普通解为 $x,y$。 那么显然有： $$\begin{cases} ax_0&+by_0&=c\\ ax&+by&=c \end{cases}$$ 我们设 $x-x_0=\triangle x$，$y-y_0=\triangle y$。 那么有： $$a(x_0+\triangle x)+b(y_0+\triangle y)=c$$ 于是得到 $$ax_0+a\triangle x+by_0+b\triangle y=c$$ 由于 $ax_0+by_0=c$，所以 $$a\triangle x+b\triangle y=0$$ 这是一个非常神秘的式子。我们需要找一组通解。 直接给结论：
\begin{cases} \triangle x&=&p\times \dfrac{b}{\gcd(a,b)} \ \ \triangle y&=-&p\times \dfrac{a}{\gcd(a,b)} \end{cases}
其中 $p$ 是任意整数。 :::info[怎么找到的通解？] 考虑人脑是如何解这个方程的，以 $4x+6y=0$ 为例。 不难考虑让 $x=6$，$y=-4$。 也就是说，令
\begin{cases} x&=b\ y&=-a \end{cases}
就可以得到一组特解。 但是 $p$ 必须是一个整数，所以你必须要让 $|x|$ 与 $|y|$ 尽可能小。 所以我们考虑令
\begin{cases} x&=\dfrac{b}{\gcd(a,b)}\ \ y&=-\dfrac{a}{\gcd(a,b)} \end{cases}
::: 那么我们得到 $$\begin{aligned} x&=x_0+\triangle x\\ &=x_0+p\times \dfrac{b}{\gcd(a,b)}\\ y&=y_0+\triangle y \\&=y_0-p\times \dfrac{a}{\gcd(a,b)} \end{aligned}$$ ### x 的最小值 根据 $$\begin{cases} x&=x_0+p\times \dfrac{b}{\gcd(a,b)}\\ y&=y_0-p\times \dfrac{a}{\gcd(a,b)} \end{cases}$$ 我们需要求出最大的 $p$ 使得 $$x\ge 1$$ 考虑推导。 $$\begin{aligned} &\ \ \ \ \ \ x\ge 1\\ &\Leftrightarrow x_0+p\times \dfrac{b}{\gcd(a,b)}\ge 1\\ &\Leftrightarrow p\times \dfrac{b}{\gcd(a,b)} \ge 1-x_0\\ &\Leftrightarrow p\ge \lceil\dfrac{1-x_0}{\frac{b}{\gcd(a,b)}}\rceil \end{aligned}$$ 最后一步取上等是因为我们不能让 $x_{min}=0$。 于是可以 $\operatorname{O}(1)$ 求。 :::info[二分方案（不推荐）] 用二分求解 $p$。 显然 $p$ 满足单调性，$p$ 越大，$x$ 越小。 缺点是该做法的复杂度是 $\operatorname{O}(\log V)$ 的。而且需要给定 $p$ 的范围，万一 $x_0$ 巨大那就不好解了。所以我们不使用这种方法。 ::: ### y 的最大值 考虑 $$ax+by=c$$ 反解得到 $$y=\dfrac{c-ax}{b}$$ 在 $\mathbb R$ 上单调递减。 那么只要 $x$ 取到 $x_{min}$，那么 $y$ 就能取到 $y_{max}$。 ### 正整数解的判断 只要 $y_{max}\le 0$，那么就没有正整数解。 ### y 的最小值 先给结论：
y_{min}=\begin{cases}y_{max}\bmod (\dfrac{a}{\gcd(a,b)}),&y_{max} \bmod (\dfrac{a}{\gcd(a,b)}) \ne 0\ \dfrac{a}{\gcd(a,b)}, &y_{max} \bmod (\dfrac{a}{\gcd(a,b)}) = 0 \end{cases}$$
证明：
考虑下面的方程：
axmax+bymin=cax_{max}+by_{min}=c
由于
axmin+bymax=cax_{min}+by_{max}=c
设 △x=xmax−xmin\triangle x=x_{max}-x_{min}，△y=ymin−ymax\triangle y=y_{min}-y_{max}。
根据上面的推导，可以得到
{△x=p×bgcd⁡(a,b)△y=−p×agcd⁡(a,b)\begin{cases} \triangle x&=&p\times \dfrac{b}{\gcd(a,b)} \\ \\ \triangle y&=-&p\times \dfrac{a}{\gcd(a,b)} \end{cases}
其中 pp 是任意整数。
由于
y_{min}&=\triangle y+y_{max}\\ &=y_{max}-p\times \dfrac{a}{\gcd(a,b)} \end{aligned}$$ 说明 $$y_{min}\equiv y_{max}(\bmod \dfrac{a}{\gcd(a,b)})$$ 由于 $y_{min}$ 必须是最小正整数，所以 $y_{min}=y_{max}\bmod \dfrac{a}{\gcd(a,b)}$。 但是这样并不严谨：因为 $y_{max}$ 可能是 $\dfrac{a}{\gcd(a,b)}$ 的倍数。所以必须加上这种情况。 ### 正整数解的个数 给结论：设答案为 $ans$，则 $$ans=\dfrac{y_{max}-y_{min}}{\frac{a}{\gcd(a,b)}}+1$$ 我们考虑用小学的植树问题来证明这个结论。 > 现在有一排树，间隔相等为 $d$，第一棵树坐标为 $x_1$，最后一棵树坐标为 $x_n$，那么一共有多少棵树？（保证 $x_n-x_1$ 是 $d$ 的倍数） 这个是很简单的：答案是 $\dfrac{x_n-x_1}{d}+1$。 考虑 $(x_1,x_n]$ 内，一定是每 $d$ 个坐标才出现一棵树，所以是区间长度与树的间距之比。由于你没有算第一棵树，所以要加 $1$。 现在我们考虑把这个问题代入到当前的情况。 把 $y$ 摁到数轴上，然后看作：第一棵树坐标 $y_{min}$，最后一棵树坐标 $y_{max}$。 根据上面的推导，树的间距是 $\dfrac{a}{\gcd(a,b)}$。 所以你就能解了。 :::info[为何每 $\dfrac{a}{\gcd(a,b)}$ 个数就会有一组解？] 很好理解。 考虑 $$ax+by=c$$ 那么 $$a(x-\dfrac{b}{\gcd(a,b)})+b(y+\dfrac{a}{\gcd(a,b)})=c$$ 那么存在一组解 $x',y'$： $$\begin{cases} x'=x-\dfrac{b}{\gcd(a,b)}\\\\ y'=y+\dfrac{a}{\gcd(a,b)} \end{cases}$$ 由于是在 $(y_{min},y_{max}]$ 区间查找，所以 $x,y\ge 1$ 恒成立。 于是证毕。 ::: ### x 的最大值 这是很简单的。 由于 $y_{min}$ 已知，所以直接把 $y_{min}$ 代进去就行。 $$ax_{max}+by_{min}=c$$ $$x_{max}=\dfrac{c-by_{min}}{a}$$ ::::error[我们没有处理无正整数解的情况！] 其实不难发现，经过上面的讨论，我们已经把没有正整数解的情况的 $x_{min}$ 与 $y_{min}$ 解出来了。 你还记得 $p\ge \lceil\dfrac{1-x_0}{\frac{b}{\gcd(a,b)}}\rceil$ 吗？此时的 $p$ 就是满足 $x_{min}\ge 0$ 的最小的 $p$。 同理我们可以发现 $y_{min}$ 在这个条件下依然成立。 :::: ::::success[P5656 代码] ``` #include<bits/stdc++.h> #define ll long long using namespace std; ll x,y; void exgcd(ll a,ll b){ if(b==0){ x=1;y=0;return; } exgcd(b,a%b); ll t=x; x=y;y=t-a/b*y; } ll a,b,c; void solve(){ scanf("%lld%lld%lld",&a,&b,&c); ll g=__gcd(a,b); if(c%g!=0){ printf("-1\n");return; } exgcd(a,b); ll x0=c/g*x,y0=c/g*y; ll p=ceil(1.0*(1-x0)/(b/g)); ll xmin=x0+p*(b/g); ll ymax=y0-p*(a/g); if(ymax<=0){ ll ymin=(ymax%(a/g)+(a/g))%(a/g); if(ymin==0)ymin=a/g; printf("%lld %lld\n",xmin,ymin); } else{ ll ymin=(ymax)%(a/g); if(ymin==0)ymin=a/g; ll cnt=(ymax-ymin)/(a/g)+1; ll xmax=(c-b*ymin)/a; printf("%lld %lld %lld %lld %lld\n",cnt,xmin,ymin,xmax,ymax); } } int main(){ int T; scanf("%d",&T); while(T--)solve(); } ``` :::: ## 例题 3 [P9796 [NERC 2018] Fractions](https://www.luogu.com.cn/problem/P9796) 给你一个整数 $n$，你需要构造出若干个形如 $\dfrac{a_i}{b_i}$ 的真分数，使得 $\sum^k_{i=1} \frac{a_i}{b_i} = 1 - \frac{1}{n}$，且 $b_i$ 可以整除 $n$。 ::::info[Solution] 先给结论。 结论：如果有解，一定存在一组 $(a,b,x,y)$，使得 $\dfrac{x}{a}+\dfrac{y}{b}=\dfrac{n}{n-1}$；如果上述条件不成立，则无解。 证明：考虑通分。 $$\dfrac{\frac{nx}{b}+\frac{ny}{a}}{n}=\dfrac{n-1}{n}$$ $$\dfrac{\frac{n(ax+by)}{ab}}{n}=\dfrac{n-1}{n}$$ $$ax+by=\dfrac{ab(n-1)}{n}$$ 根据裴蜀定理，上面方程有解的条件是 $\dfrac{ab(n-1)}{n} \bmod \gcd(a,b)=0$，也就是 $n-1 \bmod \gcd(a,b)=0$（$n$ 是 $a,b$ 的倍数）。 设 $n$ 为 $p_1^{q_1}p_2^{q_2}\cdots p_k^{q_k}$。 由于 $n-1$ 与 $n$ 没有除了 $1$ 之外的其他公因数，而 $a,b$ 都是 $n$ 的因数，所以只能让 $\gcd(a,b)=1$。 考虑令 $a=p_x^{q_x}$（其中 $x\in[1,k]$），$b=\dfrac{n}{a}$，这样 $a,b$ 之间没有公因数，则 $\gcd(a,b)=1$，符合条件，可以构造出解。 但是如果 $k=1$，则 $b=1$，显然不能够造出真分数使得有解，所以报告无解。 如果你构造多个，条件更强，更无法满足。 找出 $a,b$ 之后，只需要解不定方程 $ax+by=\dfrac{ab(n-1)}{n}$，也就是 $ax+by=n-1$ 即可。 可以用 exgcd 求出其的一组解，然后用 P5656 的代码求出其最小的正整数 $x$ 和最大的正整数 $y$ 来求正整数解。 :::success[AC Code] ``` #include<bits/stdc++.h> #define ll long long using namespace std; ll n,x,y; void exgcd(ll a,ll b){ if(b==0){ x=1;y=0;return; } exgcd(b,a%b); ll tmp=x; x=y; y=tmp-a/b*y; } //const int N=; int main(){ scanf("%lld",&n); ll a=-1,b=0; ll t=n; for(int i=2;i*i<=t;i++){ if(n%i!=0)continue; ll tmp=1; while(t%i==0){ t/=i;tmp*=i; } if(t==1){ printf("NO\n"); return 0; } a=tmp;b=n/tmp; break; } if(a==-1){ printf("NO\n"); return 0; } exgcd(a,b); printf("YES\n2\n"); ll g=__gcd(a,b); ll x0=(n-1)*x,y0=(n-1)*y; ll p=ceil(1.0*(1-x0)/(b/g)); ll xmin=x0+p*(b/g); ll ymax=y0-p*(a/g); printf("%lld %lld\n%lld %lld",xmin,b,ymax,a); return 0; } ``` ::: ::::

评论

共 6 条评论，欢迎与作者交流。

正在加载评论...