题解：AT_cf17_final_f Distribute Numbers

脑电波题，但是我似乎没有对上脑电波，搞了一个略微复杂的做法。

思路

我们可以将“任意两张纸上有且仅有一个相同的数字”转化为：遍历每种数字，找出这种数字出现的纸的集合，随后将这个集合内的纸两两连边，最后要求每两张纸之间恰好连了一条边。

那么显然有必要条件：

\frac{n(n-1)}{2}=n\frac{k(k-1)}{2}

n-1=k(k-1)

我们取出

n \in [1000,2000]

的所有满足此条件的

(n,k)

，发现还是有点多的，接下来考虑构造方案。

我们绘制一个

n \times n

的表格，横坐标表示纸，纵坐标表示值，在表格某个点

(x,y)

上染色就表示第

x

张纸上有值

y

。

我们发现合法的条件就是任意两列染色的行集合交集为 $1$ 。

我们可以考虑先把前

k

列染成下图（

n=13,k=4

）这样，不难发现前

k

列此时是满足条件的。

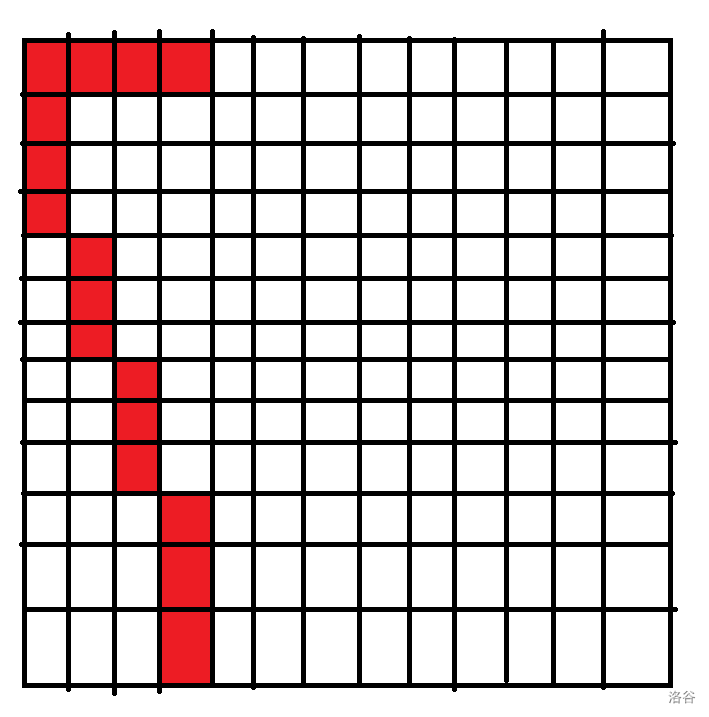
对于后面的列我们可以考虑像下面这样一直染。

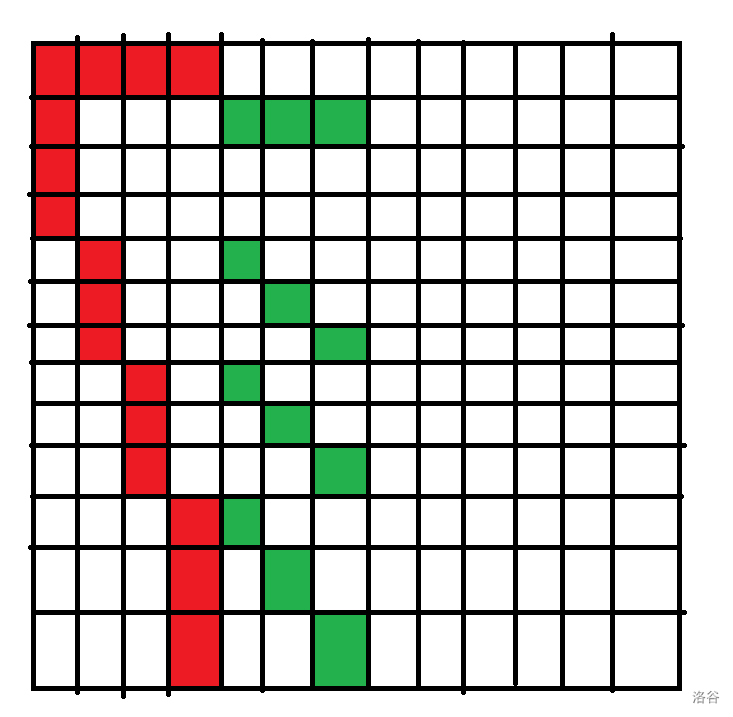
但是你发现染到第三组时就寄了。

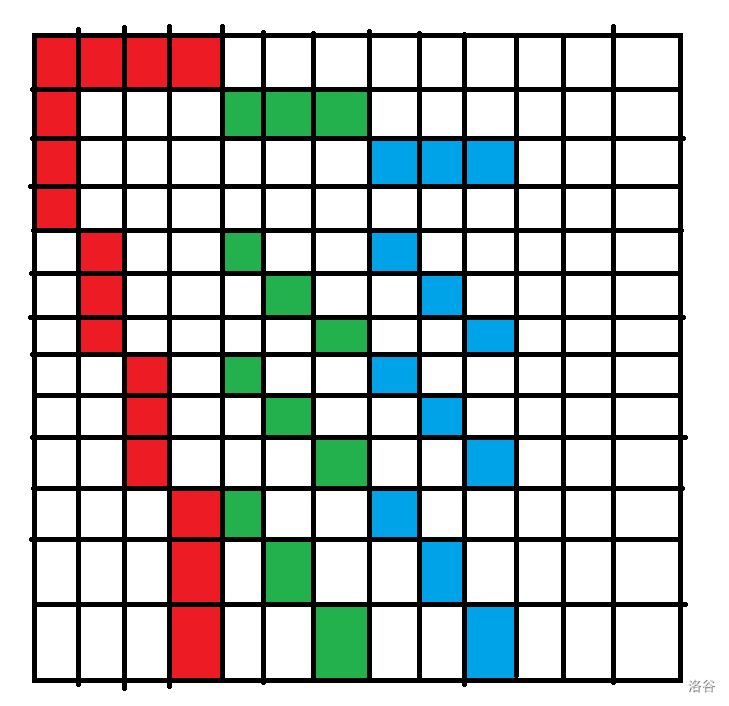
自然地，我们可以考虑将第三组错开放，也就是这样：

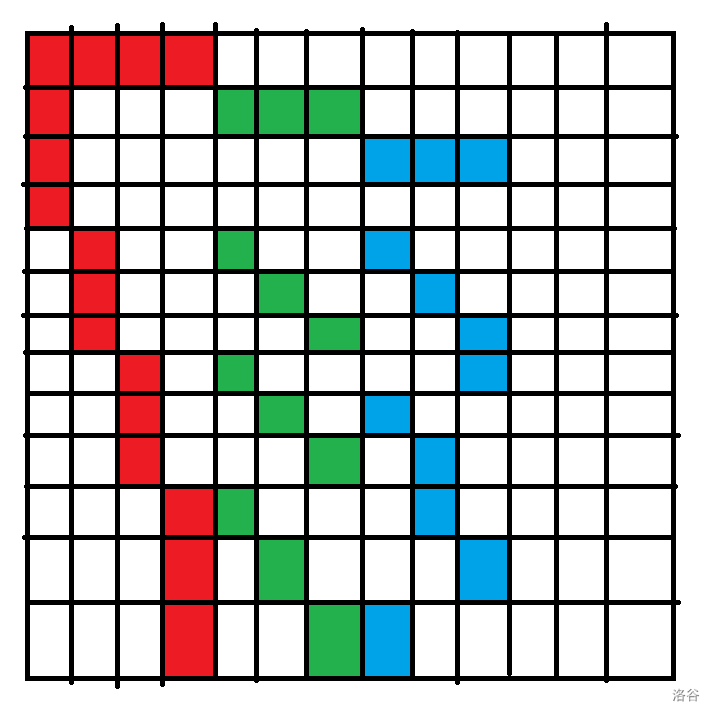
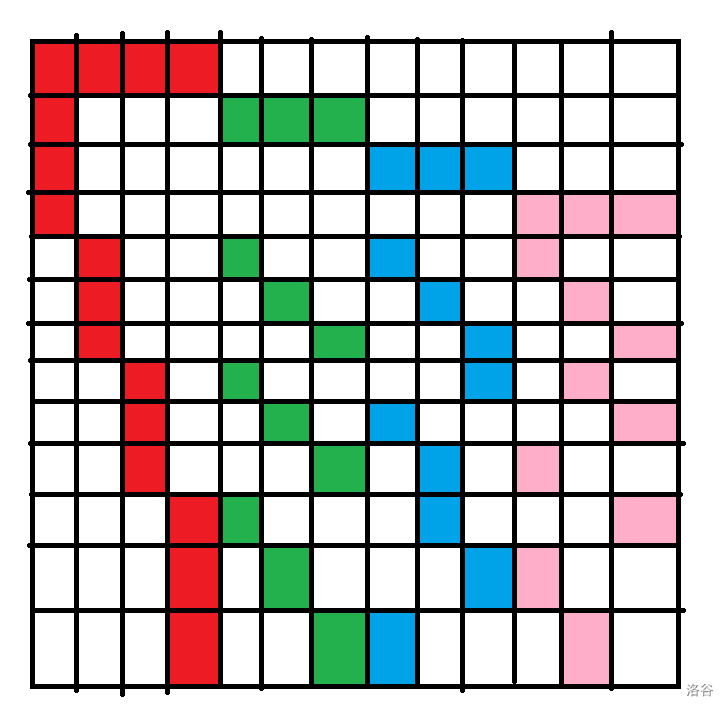
这个所谓“错开放”的策略就是：

对于前 $k$ 行我们每次放一段长度为 $k-1$ 的，与前面错开。
对于第 $k+1 \sim 2k-1$ 行，我们每次放一段边长为 $k-1$ 的正方形的主对角线。
对于第 $2k \sim n$ 行，我们每 $k-1$ 行分一组，每 $k-1$ 列分一组，都从 $0$ 开始编号。设当前列在列中是第 $i$ 组第 $j$ 个，要在第 $l$ 组行里染色，那么会染第 $l$ 组行的第 $(j+i \times l) \bmod (k-1)$ 个元素。

考虑一下这个策略何时会失效，也就是

j_1+i_1 \times l \equiv j_2+i_2 \times l \pmod {(k-1)}

（

i_1 \neq i_2

）的解数不是

1

个。

j_1+i_1 \times l \equiv j_2+i_2 \times l \pmod {(k-1)}

j_1-j_2 \equiv i_2 \times l-i_1 \times l \pmod {(k-1)}

(i_2-i_1)l + (k-1)x=j_1-j_2

al+(k-1)x=b

显然有

l \in [0,k-1)

，假设有两个不同解

a_1,a_2

，那么：

a_1l+(k-1)x_1=a_2l+(k-1)x_2

(a_1-a_2)l=(k-1)(x_2-x_1)

当

k-1

是质数时，

\gcd(l,k-1)=1

，

a_1-a_2

必须是

k-1

的倍数，但是由于

a_1 \neq a_2

且

|a_1|,|a_2| \in [0,k-1)

，这是不可能的，因此此时最多有一个解，同时根据裴蜀定理，这个方程肯定有解，那么肯定恰好一个解。

所以我们取

k-1

是质数的一组

(n,k)

，然后直接构造就做完了。

可以取

k=38

。

代码

CPP

//A tree without skin will surely die.
//A man without face will be alive.
#include<bits/stdc++.h>
using namespace std;
#define rep(i,j,k) for (int i=j;i<=k;++i)
#define per(i,j,k) for (int i=j;i>=k;--i)
vector<int>vc[2005];int a[2005][2005];
inline bool prime(int x){
	rep(i,2,x-1) if (x%i==0) return 0;
	return 1;
}
inline void solve(){
	rep(n,1000,2000) rep(k,1,n)
		if (k*(k-1)==n-1 && prime(k-1)){
			cout<<n<<' '<<k<<'\n';
			int la=2;
			vector<int>g;
			rep(i,1,k){
				vc[i].push_back(1),g.push_back(la);
				rep(j,la,la+k-2) vc[i].push_back(j);
				la=la+k-1;
			}
			int cnt=0,D=0;
			rep(i,k+1,n){
				int gadd=cnt;
				for (auto it:g){
					if (!vc[i].size()) vc[i].push_back(it+D);
					else vc[i].push_back(it+gadd);
					if (vc[i].size()>1) gadd+=D,gadd%=(k-1);
				}
				++cnt;
				if (cnt==k-1) cnt=0,++D;
			}
			rep(i,1,n) for (auto j:vc[i])
				a[j][++a[j][0]]=i;
			rep(i,1,n){
				rep(j,1,a[i][0]) cout<<a[i][j]<<' ';
				cout<<'\n';
			}
			return;
		}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int t=1;
	// cin>>t;
	while (t--) solve();
	return 0;
}

题解：AT_cf17_final_f Distribute Numbers

文章操作

思路

代码

相关推荐

评论

题解：AT_cf17_final_f Distribute Numbers