专栏文章
题解:P3374 【模板】树状数组 1
P3374题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @mipk8nxe
- 此快照首次捕获于
- 2025/12/03 13:22 3 个月前
- 此快照最后确认于
- 2025/12/03 13:22 3 个月前
题意:
有一个由 个数字组成的数列,对这个数列进行 次操作:
-
将第 个数加 。
-
输出 区间内的和。
树状数组
引入
一个包含n个数的序列 计算前 个数的和值,称为前缀和。
。
累加求前 个数的和值需要 时间。而且若对 进行修改,则 都需要修改,最坏的情况下需要 时间。
树状数组可以高效实现,其查询前缀和与点更新均为 。
那么树状数组是如何巧妙地实现呢?
正文
树状数组引入了分级管理制度,设置一个管理小组,每个管理员管理一个或多个连续的元素。例如,数列有 个元素,分别用 存储,管理数组为 。管理数组 是树状的,因此称为树状数组。
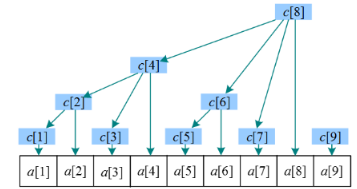
树状数组,又称为二进制索引树 ,通过二进制分解划分区间。那么 存储的是哪些值?
1.区间长度
若 的二进制表示末尾有 个连续的 ,则 存储的区间长度为 ,从 向前数 个元素,即 。

举例:
- ,即管理 个。
2.前驱和后继
-
直接前驱: 的直接前驱为 ,即 左侧紧邻的子树的根。
-
直接后继: 的直接后继为 ,即 的父节点。
-
前驱: 左侧所有子树的根。
-
后继: 的所有祖先。
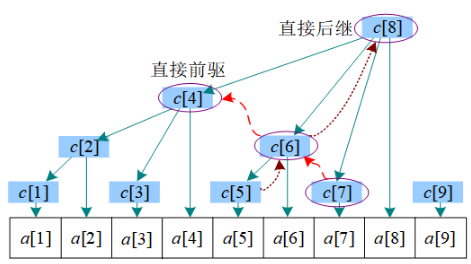
3.查询前缀和
前 个元素的前缀和 等于 加上 的前驱。
等于 加上 的前驱,。
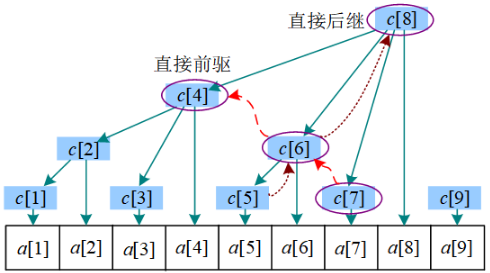
4.点更新
若对 进行修改。
- 令 加上一个数 ,则只需更新 及其后继(祖先)。
- 即令这些节点都加上 即可,无需修改其他节点。
例如,修改 ,令其加 。只需 ,然后 的后继分别加 ,即 。
5.查询区间和
若求区间和值 ,则求解前 个元素的和值减去前 个元素的和值即可。即 。
思路
套模板就行。
CPP#include<bits/stdc++.h>
using namespace std;
long long m,n,x,y,z;
long long a[1000005],c[1000005];
long long lowbit(long long i)//求lowbit
{
return (-i)&i;
}
void add(long long i,long long z)//添加操作
{
for(;i<=n;i+=lowbit(i))
c[i]=c[i]+z;
}
long long sum(long long i)//求和操作
{
long long s=0;
for(;i>0;i-=lowbit(i))
s+=c[i];
return s;
}
int main(){
scanf("%lld%lld",&n,&m);//输入
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
add(i,a[i]);
}
for(int i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&z,&x,&y);
if(z==1)add(x,y);
else printf("%lld\n",sum(y)-sum(x-1));//求区间和,输出
}
return 0;
}
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...