专栏文章

感受这股劲.jpg

GGraphcity
个人记录参与者 3已保存评论 2

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
2 条
当前快照
1 份
快照标识符
@miqmhgl2
此快照首次捕获于
2025/12/04 07:12
3 个月前
此快照最后确认于
2025/12/04 07:12
3 个月前
查看原文
热身题
已知抛物线：y=x2y=x^2，直线 ll 交抛物线于 A,BA,B 两点。分别过 A,BA,B 作抛物线的切线，两条切线交点为 QQ。若 AQAQ 垂直于 BQBQ，求 QQ 的轨迹方程。
令 A(x1,y1),B(x2,y2),Q(x0,y0)A(x_1,y_1),B(x_2,y_2),Q(x_0,y_0)，那么两条切线的斜率分别为 2x1,2x22x_1,2x_2，所以有 2x1×2x2=−12x_1\times 2x_2=-1，x1x2=−14x_1x_2=-\dfrac{1}{4}。
同时有 lAB:xx0=12(y+y0)l_{AB}: xx_0=\dfrac{1}{2}(y+y_0)，那么 A,BA,B 一定满足 xx0=12(x2+y0)xx_0=\dfrac{1}{2}(x^2+y_0)，这是一个一元二次方程，根据韦达定理，x1x2=y0=−14x_1x_2=y_0=-\dfrac{1}{4}。所以 QQ 的轨迹方程就是 y=−14y=-\dfrac{1}{4}。
所以我们就 ⋯⋯\cdots\cdots 解决了？为什么这么快？
我们再来看一道热身题：
热身题 - 变式
已知抛物线：y=x2y=x^2，RR 为抛物线上任意一点，作圆 W:x2+(y−2)2=1W: x^2+(y-2)^2=1 的两条切线分别交抛物线于 A,BA,B 两点。试判断直线 ABAB 与圆 WW 的关系。
答案肯定是相切。如果不是相切就不会这样考你了
但是为什么呢？
令 R(x0,y0),A(x1,y1),B(x2,y2)R(x_0,y_0),A(x_1,y_1),B(x_2,y_2)。
构造过 R,AR,A 的直线。先从方程 (x−x0)(x−x1)=0(x-x_0)(x-x_1)=0 开始。x2−(x0+x1)x+x0x1=0x^2-(x_0+x_1)x+x_0x_1=0。代入 y=x2y=x^2，就可以得到 y−(x0+x1)x+x0x1=0y-(x_0+x_1)x+x_0x_1=0。这个就是 lRAl_{RA} 的方程了。
由于它与圆相切，想到点到直线的距离公式。d(W,lRA)=∣x0x1+2∣(x0+x1)2+1=1d(W,l_{RA})=\dfrac{|x_0x_1+2|}{\sqrt{(x_0+x_1)^2+1}}=1，整理一下，就是 (x0x1+2)2=(x0+x1)2+1(x_0x_1+2)^2=(x_0+x_1)^2+1，(x02−1)x12+2x0x1+3−x02=0(x_0^2-1)x_1^2+2x_0x_1+3-x_0^2=0。
注意到这个对于 x2x_2 也是成立的，代入 y=x2y=x^2，可以得到 (x02−1)y+2x0x+3−x02=0(x_0^2-1)y+2x_0x+3-x_0^2=0，这个就是 lABl_{AB} 的方程。
再算一次点到直线的距离看看：d(W,lAB)=∣2(x02−1)+3−x02∣4x02+(x02−1)2d(W,l_{AB})=\dfrac{|2(x_0^2-1)+3-x_0^2|}{\sqrt{4x_0^2+(x_0^2-1)^2}}。为了方便，代入 y0=x02y_0=x_0^2，原式等于 ∣2(y−1)+3−y∣4y+(y−1)2=y+1y2+2y+1=1\dfrac{|2(y-1)+3-y|}{\sqrt{4y+(y-1)^2}}=\dfrac{y+1}{\sqrt{y^2+2y+1}}=1，成立！
所以我们就 ⋯⋯\cdots\cdots 解决了？为什么这么快？
我们再来看一道有点难度的题目：
Test Yourself！
若椭圆 x2a2+y2b2=1 (a>b>0)\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>b>0) 的两个焦点和两个顶点共圆，则称它为「完美椭圆」。已知 EE 为「完美椭圆」，且 EE 与 l1:x+6y=4l_1:x+\sqrt 6y=4，l2:x−6y=4l_2:x-\sqrt 6y=4 均相切。
  1. 求 EE 的方程。
  2. 已知动点 PP 在 EE 的第一象限上运动，lPl_P 和 PP 相切，和 l1,l2l_1,l_2 分别交于 C,DC,D。设右焦点为 F1F_1，请证明 ∠CF1D\angle CF_1D 为定值，并求其正切值。
注意：本题在网上的答案几乎 都是错误的。
第一问是高考特色：给出一个完全没有用，用完即扔，对解题没有任何指导意义的新定义。
E:x24+y22=1E:\dfrac{x^2}{4}+\dfrac{y^2}{2}=1。
重点是第二问。正切值给定提示比较明显，你需要求出 CF1CF_1 和 F1DF_1D 这两条直线的斜率。
令 P(x0,y0),C(x1,y1),D(x2,y2)P(x_0,y_0),C(x_1,y_1),D(x_2,y_2)。
我们先想办法把 CC 和 DD 凑到一块去。注意到 l1,l2l_1,l_2 两条直线的方程非常相似，可以利用平方的方法把正负号消掉，就可以得到一个方程：6y2=(4−x)26y^2=(4-x)^2。对于 lPl_P，我们又有一个方程 lP:xx0+2yy0=4l_P:xx_0+2yy_0=4，也就是 y=4−xx02y0y=\dfrac{4-xx_0}{2y_0}。
把 yy 代入二次方程中，可以得到：(3x02−2y02)x2+(16y02−24x0)x+(48−32y02)=0(3x_0^2-2y_0^2)x^2+(16y_0^2-24x_0)x+(48-32y_0^2)=0。
为了简化这个式子，我们需要把 x0,y0x_0,y_0 其中的一个消掉。注意到 y0y_0 出现的次数全是二次，所以我们这里选择消掉 y0y_0。椭圆曲线中有 2y02=4−x022y_0^2=4-x_0^2，代入得到 (x02−1)x2+(−2x02−6x0+8)x+4(x02−1)=0(x_0^2-1)x^2+(-2x_0^2-6x_0+8)x+4(x_0^2-1)=0。
注意到中间的式子可以因式分解，同除 x0−1x_0-1 可得 (x0+1)x2−2(x0+4)x+4(x0+1)=0(x_0+1)x^2-2(x_0+4)x+4(x_0+1)=0。
看看我们得到了什么？x1x2=4x_1x_2=4！！！这下稳了。
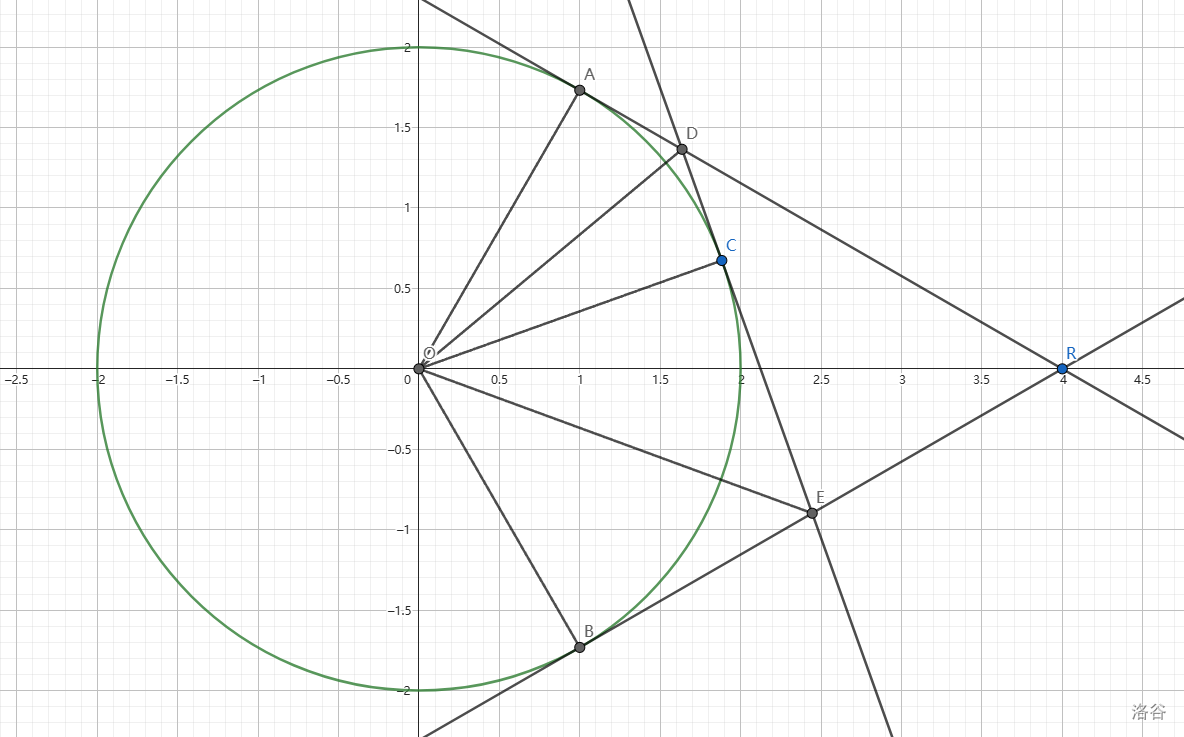
仿射变换可以得到相同的结果。
我们把每个点的 yy 坐标扩大到原来的 2\sqrt 2 倍，这样椭圆就可以变成一个半径为 2 的圆。两条直线就会变成 l1:x+3y=4l_1:x+\sqrt 3y=4 和 l2:x−3y=4l_2:x-\sqrt 3y=4。可以发现，这两条直线与 xx 轴形成的夹角刚好是 30∘30^\circ！
同时我们注意到：OD,OEOD,OE 分别是 ∠AOC,∠COB\angle AOC,\angle COB 的角平分线。又因为 ∠AOB=180∘−∠DRB=120∘\angle AOB=180^\circ-\angle DRB=120^\circ，所以 ∠DOE=60∘\angle DOE=60^\circ。
令 ∠DOR=θ\angle DOR=\theta，那么 ∠EOR=60∘−θ\angle EOR=60^\circ-\theta。同时，对于 D,ED,E 两点，有 3∣yi∣=4−xi\sqrt 3|y_i|=4-x_i，同除 xix_i，令 ki=yixi={tan⁡θi=1tan⁡(60∘−θ)i=2k_i=\dfrac{y_i}{x_i}=\begin{cases}\tan\theta & i=1\\ \tan(60^\circ-\theta) &i=2\end{cases}，有 3ki=4xi−1\sqrt 3k_i=\dfrac{4}{x_i}-1。
代入 tan⁡∠DOE=k1+k21−k1k2=3\tan\angle DOE=\dfrac{k_1+k_2}{1-k_1k_2}=\sqrt 3，也就是 3(k1+k2)=3−3k1k2\sqrt 3(k_1+k_2)=3-3k_1k_2，4x1−2+4x2−2=3−(4x1−1)(4x2−1)\dfrac{4}{x_1}-2+\dfrac{4}{x_2}-2=3-(\dfrac{4}{x_1}-1)(\dfrac{4}{x_2}-1)。
最终化简得到 x1x2=4x_1x_2=4。
CF1,DF1CF_1,DF_1 的斜率分别为 k1=y1x1−2k_1=\dfrac{y_1}{x_1-\sqrt 2} 和 k2=y2x2−2k_2=\dfrac{y_2}{x_2-\sqrt 2}。
现在我们有两个方法，一个是代入 tan⁡θ=k1−k21+k1k2\tan\theta=\dfrac{k_1-k_2}{1+k_1k_2} 然后使用非对称韦达。另一种是直接带入 x2=4x1x_2=\dfrac{4}{x_1} 然后爆算。这两种方法都可以算出来答案是 tan⁡θ=−(3+62)\tan\theta=-(\sqrt 3+\dfrac{\sqrt{6}}{2})。
有没有一些更加简单的办法呢？
我们考虑代入 y1=4−x16y_1=\dfrac{4-x_1}{\sqrt 6}，y2=4−x2−6y_2=\dfrac{4-x_2}{-\sqrt 6}，然后带入进 tan⁡θ\tan \theta 的表达式，可以发现它其实就是在求这样一个东西：令 ti=4−xixi−2t_i=\dfrac{4-x_i}{x_i-\sqrt 2}，则 tan⁡θ=6×t1+t2−6+t1t2\tan\theta=\sqrt 6\times \dfrac{t_1+t_2}{-6+t_1t_2}。
整理一下，可以得到 xi=4+2titi+1x_i=\dfrac{4+\sqrt 2t_i}{t_i+1}，结合 x1x2=4x_1x_2=4 有 2t1t2−12=(42+4)(t1+t2)2t_1t_2-12=(4\sqrt 2+4)(t_1+t_2)，解得 t1+t2t1t2−6=−122+2\dfrac{t_1+t_2}{t_1t_2-6}=-\dfrac{1}{2\sqrt 2+2}，有 tan⁡θ=−(3+62)\tan\theta=-(\sqrt 3+\dfrac{\sqrt{6}}{2})！！！
我们一起来感受这股劲：为什么我们可以通过这样一些巧妙的办法解决这三道问题呢？
回顾这三道题中解法的关键一步：我们通过方程把两个不同的点连接了起来。
为什么我们可以这样做？这里给出三种可能的解释：
  1. 对称性。三道题中 x1,x2x_1,x_2 的形式上有非常多的对称之处。
  2. 曲线系。虽然我一直只是知道有这么个东西，但是有可能这三道题中我们偷偷地使用了它。
  3. 韦达定理。三道题中最终的过程都跟 val1+val2val_1+val_2 和 val1×val2val_1\times val_2 这两个东西紧密相关。虽然我暂且还不知道这两个东西到底能不能跟韦达定理扯上关系，但毫无疑问它们肯定非常有用。

评论

共 2 条评论，欢迎与作者交流。

正在加载评论...