专栏文章

题解：P13273 [NOI2025] 数字树

IIvanZhang2009
P13273题解参与者 7已保存评论 6

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
6 条
当前快照
1 份
快照标识符
@miousg19
此快照首次捕获于
2025/12/03 01:29
3 个月前
此快照最后确认于
2025/12/03 01:29
3 个月前
查看原文
神题。
先给出一个正解无关的平方暴力。
考虑如何刻画一个 dfs 序。实际上就是每个非叶子节点选一下先走左边还是右边。所以说总共的 dfs 序个数是 22n−12^{2n-1}。
考虑一个得到序列是可消除的的充要条件：对于任意两种颜色 aa 和 bb，它们的出现都不是 a,b,a,ba,b,a,b 这样交错的。我们可以直接枚举两种颜色，然后讨论一下它们的位置关系。
这里从合并的角度理解。由于给定了四个叶子节点，相当于每次选两个合并成一个。如果两个同色的先合起来了，那就没啥意义，一定合法。所以考虑第一步是把一对 a,ba,b 合起来了。有以下两种情况：
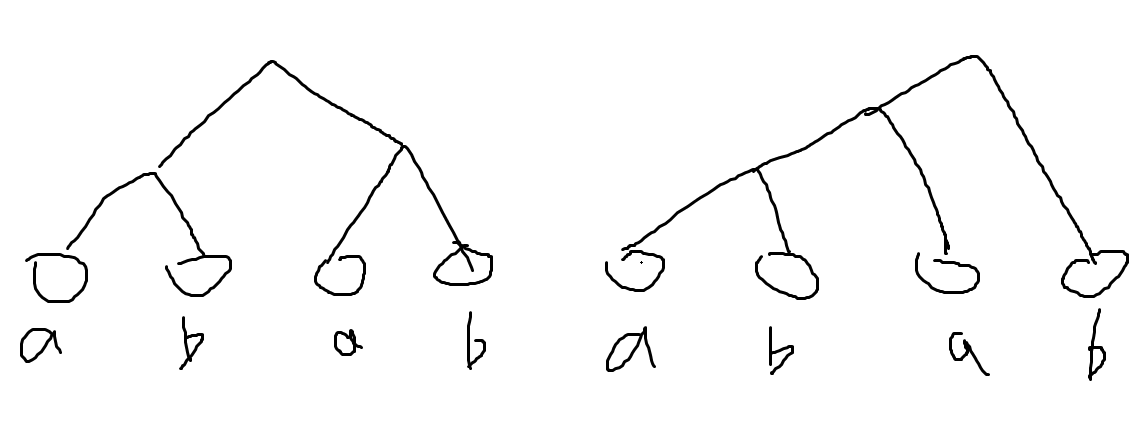
（图糙勿喷）。
第一种相当于 A 性质。可以发现考虑两个偏下的 lca，如果第一个先往左，则第二个必须先往右；第一个先往右，则第二个必须先往左。反之亦然。可以理解为这两个 lca 的往下遍历的顺序是“绑定”的。
第二种也可以考虑两个偏下的 lca。下面的 bb 一定不能插在两个 aa 中间，所以两个偏下的 lca 中“偏上的那个先往右”和“偏下的那个先往左”是充要的。也就是说这两个 lca 的往下遍历顺序也是“绑定”的。
于是可以想到把两种情况中两个绑定的节点连一条边。由于保证了有解，我们可以在任意一种合法的条件下调整：两个有边相连的点的往下遍历顺序必须同时翻转。这相当于每个连通块可以选择是否翻转。维护一下连通块个数即可，使用并查集。每次询问的时候枚举新颜色和一个老颜色之间的限制即可。时间复杂度 O(n2)O(n^2)。
由于这个有影响的点对都是新加入的一对点的祖先，所以对于 B 性质我们直接枚举这两个祖先检查即可，使用哈希表，时间复杂度 O(nlog⁡2n)O(n\log^2n)，可能需要一定卡常。
可以在完全没有正解观察的情况下获得 8080 分。
正解需要观察到性质：记一个子树的权值为子树内恰出现一次的颜色的集合。记 cc 为本质不同的大小至少是 22 的这种集合的个数，则答案为 22n−1−c2^{2n-1-c}。
具体地，仍然考虑在合法解上调整。称两个子树在同一个等价类当且仅当两个子树的权值相同。即 cc 为等价类个数。对于每个出现了两种只有一次出现的颜色的等价类，我们声称每个等价类必须有偶数个被翻转方向。首先所有同等价类的子树的根必须在同一条路径上，而且集合内的颜色都是跨过这些根的。翻转一个这样的点就会导致至少两个点顺序反过来。那么翻转奇数个点一定会让某一侧反过来，另一侧不变，就出现矛盾。具体地，可以画一些 A 性质的图理解一下。而注意到 ∑i=0n[2∣i](ni)=2n−1(n≥1)\sum_{i=0}^n[2\mid i]\binom ni=2^{n-1}(n\ge 1)，也就是说每个等价类会把总方案数除以 22。所以你把初始的答案除以 2c2^c 就是答案。
现在问题就是：每次给你两个点，把路径上除了 lca 的点的集合内都加入这种新颜色，然后求每次加入颜色后的足够大的等价类个数。
天才地考虑每个点正解用 01 串来表示这个集合。第 ii 次操作即把路径上除了 lca 的点的 01 串的第 ii 为改成 11。这样前 ii 次操作后就相当于每个点的 01 串的长度为 ii 的前缀。
这样的去重问题我们考虑按字典序排序。假设我们可以把所有的这样的串按照字典序排序，这样重复的部分就只要考虑相邻两个串的 lcp。具体地，对于第 jj 个串，我们只从 jj 和 j−1j-1 两个串的 lcp 长度的下一次操作开始考虑。这里顺便也要求一下每个串的第二个 11 的出现位置。
维护 01 串并比较字典序就是经典的线段树合并问题了。考虑线段树维护每个区间的 11 位置的哈希值（直接使用随机赋权 xor hash！！！）以及前两个 11 的位置。然后比较两个串的字典序可以使用线段树二分，比较左子树的哈希值是否相同即可；求 lcp 也可以用同样的方法。这样 cmp 的复杂度是 O(log⁡n)O(\log n)，加上排序，时间复杂度 O(nlog⁡2n)O(n\log^2n)，跑得飞快。
可以通过一层一层比较做到 O(nlog⁡n)O(n\log n)，具体就是把左边哈希值相同的放一起。据说跑的没 O(nlog⁡2n)O(n\log^2n) 快，所以懒得写了。
CPP
#include<bits/stdc++.h>
#define MOD 998244353
#define int long long
#define REP(i,a,n) for(int i=a;i<(int)(n);++i)
#define pb push_back
#define all(v) v.begin(),v.end()
#define pii pair<int,int>
#define cntbit(x) __builtin_popcount(x)
using namespace std;
int qpow(int x,int y){
	int res=1;
	while(y)res=y&1? res*x%MOD:res,x=x*x%MOD,y>>=1;
	return res;
}
int ID;
int n;
int L[400005],R[400005];
int ls[32000005],rs[32000005];
int fa[800005];
int dep[800005];
int cnt[800005];
int dfn[800005],dtot;
int st[20][800005];
void dfs(int x){
	st[0][dfn[x]=dtot++]=fa[x];
	if(x<2*n-1)dfs(L[x]),dfs(R[x]);
}
int getmax(int x,int y){return dep[x]<dep[y]? x:y;}
int getlca(int x,int y){
	if(x==y)return x;
	if((x=dfn[x])>(y=dfn[y]))swap(x,y);
	int s=__lg(y-(++x)+1);
	return getmax(st[s][x],st[s][y-(1<<s)+1]);
}
vector<int>add[800005],del[800005];
int colval[800005];
mt19937 sd(random_device{}());
uniform_int_distribution<int>rd(64,(1ull<<63)-1);
struct node{
	int h;//哈希值
	int p1,p2;
	node operator +(node a){
		if(p1==n){
			a.h^=h;
			return a;
		}else if(p2!=n)return {h^a.h,p1,p2};
		else return {h^a.h,p1,a.p1};
	}
}seg[32000005];
int tot;
int merge(int l,int r,int p1,int p2){
	if(!p2)swap(p1,p2);
	if(!p1)return p2;
	int p=tot++;
	if(l==r){
		seg[p].h=seg[p1].h^seg[p2].h;
		seg[p].p1=seg[p].p2=n;
		if(seg[p1].p1!=n)seg[p].p1=seg[p1].p1;
		if(seg[p2].p1!=n)seg[p].p1=seg[p2].p1;
		return p;
	}
	int m=(l+r)>>1;
	ls[p]=merge(l,m,ls[p1],ls[p2]);
	rs[p]=merge(m+1,r,rs[p1],rs[p2]);
	seg[p]=seg[ls[p]]+seg[rs[p]];
	return p;
}
int update(int pos,int l,int r,int p1,int op){
	int p=tot++;
	if(l==r){
		if(op==1)seg[p]={colval[l],l,n};
		else seg[p]={0,n,n};
		return p;
	}
	ls[p]=ls[p1];rs[p]=rs[p1];
	int m=(l+r)>>1;
	if(m>=pos)ls[p]=update(pos,l,m,ls[p],op);
	else rs[p]=update(pos,m+1,r,rs[p],op);
	seg[p]=seg[ls[p]]+seg[rs[p]];
	return p;
}
int rt[800005];
void dfs2(int x){
	if(x>=2*n-1)return;
	dfs2(L[x]);dfs2(R[x]);
	rt[x]=merge(0,n-1,rt[L[x]],rt[R[x]]);
	for(auto i:add[x])rt[x]=update(i,0,n-1,rt[x],1);
	for(auto i:del[x])rt[x]=update(i,0,n-1,rt[x],0);
}
bool cmp(int l,int r,int p1,int p2){
	if(!p1)return 1;else if(!p2)return 0;
	if(l==r)return seg[p1].h<seg[p2].h;
	int m=(l+r)>>1;
	if(seg[ls[p1]].h==seg[ls[p2]].h)return cmp(m+1,r,rs[p1],rs[p2]);
	else return cmp(l,m,ls[p1],ls[p2]);
}
bool Cmp(int x,int y){if(seg[rt[x]].h==seg[rt[y]].h)return x<y;else return cmp(0,n-1,rt[x],rt[y]);}
int lcp(int l,int r,int p1,int p2){
	if(!p1&&!p2)return r-l+1;
	else if(!p1)return seg[p2].p1-l;
	else if(!p2)return seg[p1].p1-l;
	else if(seg[p1].h==seg[p2].h)return r-l+1;
	else if(l==r)return 0;
	int m=(l+r)>>1;
	if(seg[ls[p1]].h==seg[ls[p2]].h)return m-l+1+lcp(m+1,r,rs[p1],rs[p2]);
	else return lcp(l,m,ls[p1],ls[p2]);
}
void Main() {
	cin>>ID>>n;
	REP(i,0,2*n-1)cin>>L[i]>>R[i],--L[i],--R[i],fa[L[i]]=fa[R[i]]=i;
	dep[0]=0;
	REP(i,1,n*4-1)dep[i]=dep[fa[i]]+1;
	dfs(0);
	REP(j,0,__lg(4*n-2)){
		REP(i,1,4*n-(1<<(j+1)))st[j+1][i]=getmax(st[j][i],st[j][i+(1<<j)]);
	}
	REP(i,0,n){
		int x,y;
		cin>>x>>y;
		--x,--y;
		int lca=getlca(x,y);
		add[fa[x]].pb(i);add[fa[y]].pb(i);del[lca].pb(i);
		colval[i]=rd(sd);
	}
	tot=1;seg[0]={0,n,n};
	dfs2(0);
	vector<int>a(2*n-1,0);iota(all(a),0);
	sort(all(a),Cmp);
	vector<int>b=a;
	REP(i,0,a.size())b[i]=seg[rt[a[i]]].p2;
	REP(i,1,a.size())b[i]=max(b[i],lcp(0,n-1,rt[a[i]],rt[a[i-1]]));
	vector<int>res(n+1,0);
	REP(i,0,a.size())++res[b[i]];
	REP(i,1,n)res[i]+=res[i-1];
	REP(i,0,n)cout<<qpow(2,2*n-1-res[i])<<'\n';
}
signed main(){
	int tc=1;
	while(tc--)Main();
	return 0;
}

评论

共 6 条评论，欢迎与作者交流。

正在加载评论...