Solution of CF207B3 Military Trainings

It is first easy to think of duplicating the sequence over and over again, breaking the ring into a chain, with each query i.e. querying a sub-segment answer.

Let $f_i$ be transferable from $j=x$ or $j=y$, and consider a greedy.

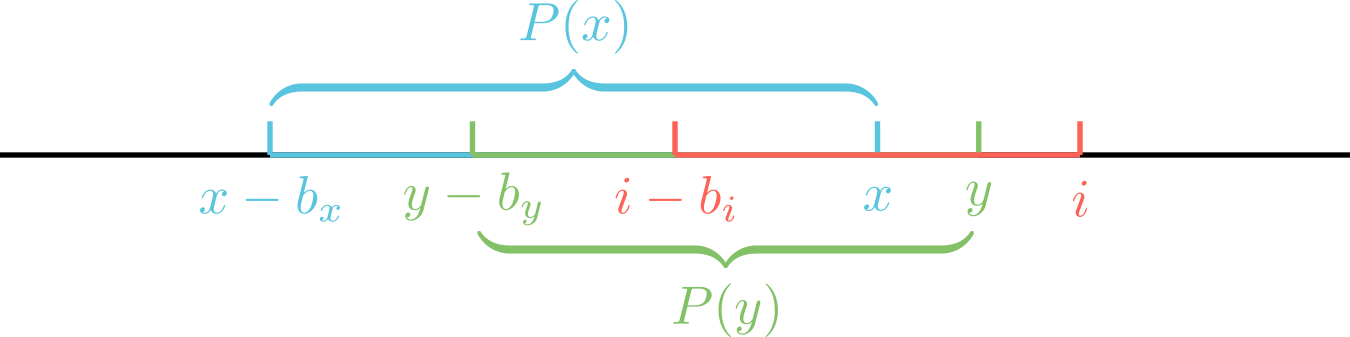
where $P(k)$ denotes the points from which $f_k$ can be transferred, i.e. $P(k)=[k-p_k,k-1]$.

Since $k-1\in P(k)$ holds, we do not need to consider the contribution of the interval $[i-p_i,k-1]$. Instead, $[y-p_y,i-p_i]\subseteq[x-p_x,i-p_i]$, i.e., all points that can be transferred to $y$ can be transferred to $x$, so it is sufficient to choose a transfer from $x$. That is, it is not inferior to transfer from the smaller $k$ of $k-p_k$. Maintained in ST tables, complexity $\mathcal{O}(n\log n+\text{ans})$.

You submited the code and found it accepted in the simulation game. You can use multiplicative preprocessing to figure out where you can jump $2^n$ steps, optimising to $\mathcal{O}(n\log n)$.