专栏文章

AGC065D Not Intersect 题解

ddspt
AT_agc065_d题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@mipv1t91
此快照首次捕获于
2025/12/03 18:24
3 个月前
此快照最后确认于
2025/12/03 18:24
3 个月前
查看原文
@RedreamMer 题解重制版。再次拜谢 ZAK 的做法。
 

Raney 引理

对于整数序列 a0,…,an−1a_0,\dots,a_{n-1}，如果 ∑a=1\sum a=1，那么 aa 的 nn 个循环移位的序列中恰好有一个满足：该序列的所有前缀和均为正整数。
证明：构造周期为 nn，定义域为 Z\Z 的函数 f(x)f(x)，满足 f(x)=f(x−1)+a(x−1) mod nf(x)=f(x-1)+a_{(x-1)\bmod n}。
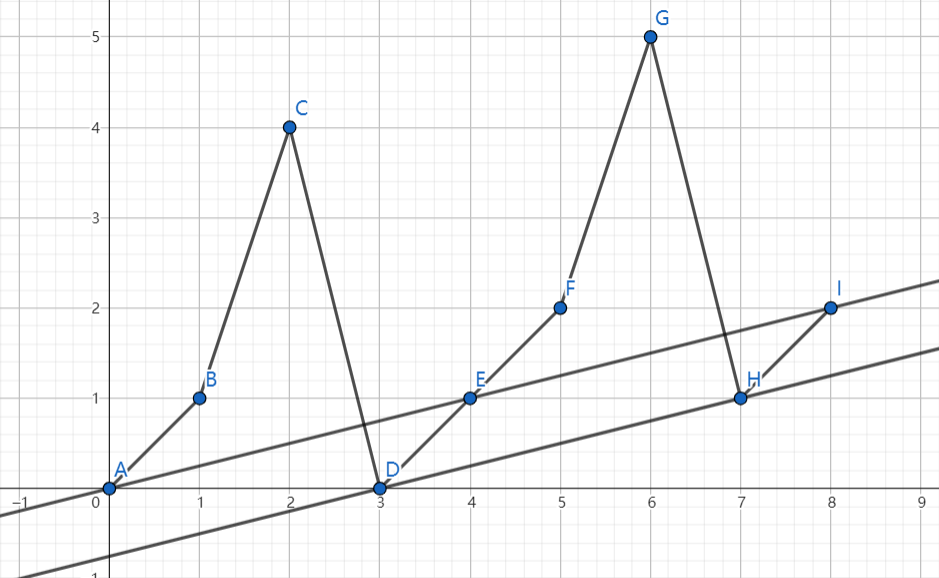
偷了张图，这是序列 a={ 1,3,−4,1 }a=\set{1,3,-4,1} 构造出的函数。
用直线 y=xn+by=\frac xn+b 从 b=−∞b=-\infin 处往上平移去切函数图像。图中切线为 DHDH。
此切线与 f(x)f(x) 在一个周期中恰好切于一个整点。
这里认为周期是 [x,x+T)[x,x+T)。容易说明切点是整点。设切点为 (x0,y0)(x_0,y_0)。因为直线的斜率为 1n\frac1n，所以直线 y=xn+by=\frac xn+b 除了在 x0x_0 处，在该周期内的其它函数值均不为整数，不可能与 f(x)f(x) 相切。
从 x0x_0 开始的循环移位就是我们要求的：序列的所有前缀和均为正整数的那个循环移位。
还要说明其它循环移位的序列均存在某个前缀和不是正整数。容易说明其它循环移位的序列在 x0x_0 之前的前缀和 ≤0\le0。
引理证毕。
例题：P6672 清华集训 2016 你的生命已如风中残烛
我们还需要用到另一个引理：
对于整数序列 a0,…,an−1a_0,\dots,a_{n-1}，如果 ∑a=1\sum a=1，那么 aa 的 nn 个循环移位的序列均不相同。
对于 n=1n=1 显然成立。对于 n>1n>1，考虑反证法。如果有两个循环移位的序列相同，那么存在周期 T<nT<n，使得 ai=a(i+T) mod na_i=a_{(i+T)\bmod n}。
从 ii 开始在模 nn 意义下不停以步长为 TT 的步跳，跳到的点均和 aia_i 相等。容易说明等价类大小为 ngcd⁡(T,n)\frac n{\gcd(T,n)}，可以进一步得到 ngcd⁡(T,n)∣∑a\frac n{\gcd(T,n)}\mid\sum a。
在 n>1n>1 时，ngcd⁡(T,n)\frac n{\gcd(T,n)} 也大于 11。∑a=1\sum a=1 需要是某个大于 11 的数的倍数，假设不成立。
引理证毕。
 

构造双射

以下的讨论均对于 n≥3n\ge3。
把圆看成一个正 nn 边形。加的 mm 条边相当于在对正 nn 边形进行划分。
正 nn 边形上相邻的两点之间的边是否连接不会对划分的形态产生影响，不妨枚举有多少条这样的边。设有 ii 条，方案数为 (ni)\binom ni。现在问题变成了要连接 m−im-i 条边，连接的边不能与原来正 nn 边形上的边重合，问可以得到多少本质不同的正 nn 边形划分。
破环为链。容易发现限制不会产生变化。
构造双射。假设有个栈，初始为空。我们要把 j:2→nj:2\to n 依次加入栈中。在任意时刻可以选择：
  • 把 jj 加入栈中
  • 此时栈顶为 jj，选择一个正整数 kk，弹出栈顶的 k+1k+1 个数。视为 jj 与当前栈顶连一条边。如果栈里没有点，那么就是 jj 和 11 连边。连完边后再把 jj 放回去。
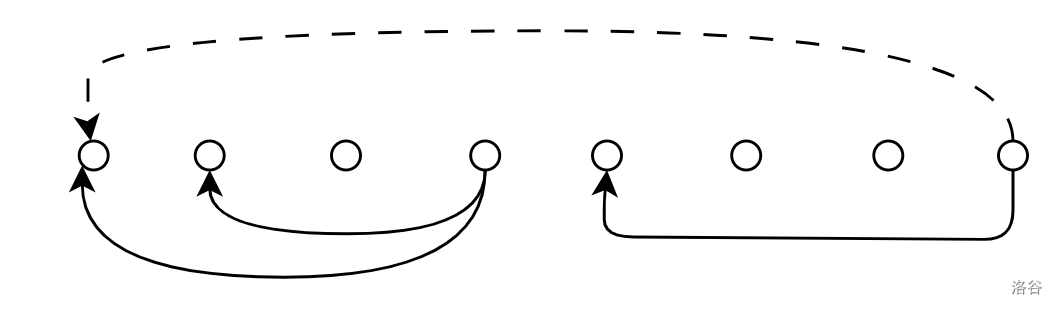
如图，这样的图形可以用以下的流程描述。
操作栈
加入 j=2j=2{ 2 }\set{2}
加入 j=3j=3{ 2,3 }\set{2,3}
加入 j=4j=4{ 2,3,4 }\set{2,3,4}
取 k=1k=1，连边 4→24\to2{ 2,4 }\set{2,4}
取 k=1k=1，连边 4→14\to1{ 4 }\set{4}
加入 j=5j=5{ 4,5 }\set{4,5}
加入 j=6j=6{ 4,5,6 }\set{4,5,6}
加入 j=7j=7{ 4,5,6,7 }\set{4,5,6,7}
加入 j=8j=8{ 4,5,6,7,8 }\set{4,5,6,7,8}
取 k=2k=2，连边 8→58\to5{ 4,5,8 }\set{4,5,8}
主播主播，有没有更加深刻的理解？有的，当然有的。
栈中的数和 11 就是当前所有可以连边的点。每次连边的时候可供连边的点都会减少。这同时保证了不会连出相邻的边。
这个过程其实就是扫描边的右端点 jj。把所有右端点为 jj 的边按左端点从右往左的顺序加入。
其实这样会存在一个问题。就是边 n→1n\to1。这条边属于相邻的边，其实是不应该存在的。但是在上面的过程中，只要把最后一步改成 k=4k=4，就会连出这样的边。
解决的方式是我们钦定必须有边 n→1n\to1（但这条边实际上不存在）。这样做的好处在于：
  • 任意合法的图按照上述方式构造操作序列后，栈中剩余的数数量 >1>1，取 k=k= 栈中剩余的数数量 −1-1 就能把边 n→1n\to1 这条边加上。双射的性质没有变，同时解决了会连出 n→1n\to1 的情况。
  • 设加入点为 +1+1，连边为 −k-k，得到的操作序列和为 11（栈中最后只剩 nn 这一个数）。
 

计算答案

特判掉 n≤2n\le2。对于 n≥3n\ge3，套用 Raney 引理计算答案。
假设我们有一个操作序列：序列中有 n−1n-1 个 +1+1，m−i+1m-i+1 个负数，这些数的和为 11。但是这个序列可能是不合法的。序列合法的条件是：栈中任意时刻都要有至少一个数，即序列的所有前缀和均为正整数。
根据 Raney 引理，这个序列的循环同构中恰好有一个是合法的。又通过前面的引理可以得到，这个序列所有的循环同构都不相同。这样就不会计重了！
容易发现根据当前的计算方式，可以得到 m−i+1≤n−2m-i+1\le n-2。因为 i≤ni\le n，所以只有 m≤2n−3m\le2n-3 时答案才不为 00。
令 k=m−i+1k=m-i+1。只要统计合法操作序列数量即可，每个合法操作序列对答案的贡献是 1n−1+k\frac1{n-1+k}。有 m−i+1m-i+1 个负数，这些数的和为 2−n2-n。先给每个数分配 −1-1，还剩 n−2−kn-2-k 个负单位可以分配。插个板得到 (n−2−1k−1)\binom{n-2-1}{k-1}。然后要把 n−1n-1 个 +1+1 和 kk 个负数归并在一起。方案数为 (n−1+kk)\binom{n-1+k}k。
总答案：
∑i=0min⁡(n,m)1n−1+k(ni)(n−3k−1)(n−1+kk)\sum_{i=0}^{\min(n,m)}\frac 1{n-1+k}\binom ni\binom{n-3}{k-1}\binom{n-1+k}k
时间复杂度 O(n)O(n)。代码。

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...