专栏文章
暑假专题9 二分图匹配与网络流应用
个人记录参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @miocuycf
- 此快照首次捕获于
- 2025/12/02 17:07 3 个月前
- 此快照最后确认于
- 2025/12/02 17:07 3 个月前
Hall 定理
二分图左右部点集合为 , 有完美匹配等价于 , 为与 相连的点集。
推广:二分图最大匹配为 。
证明:原式 。如下图:
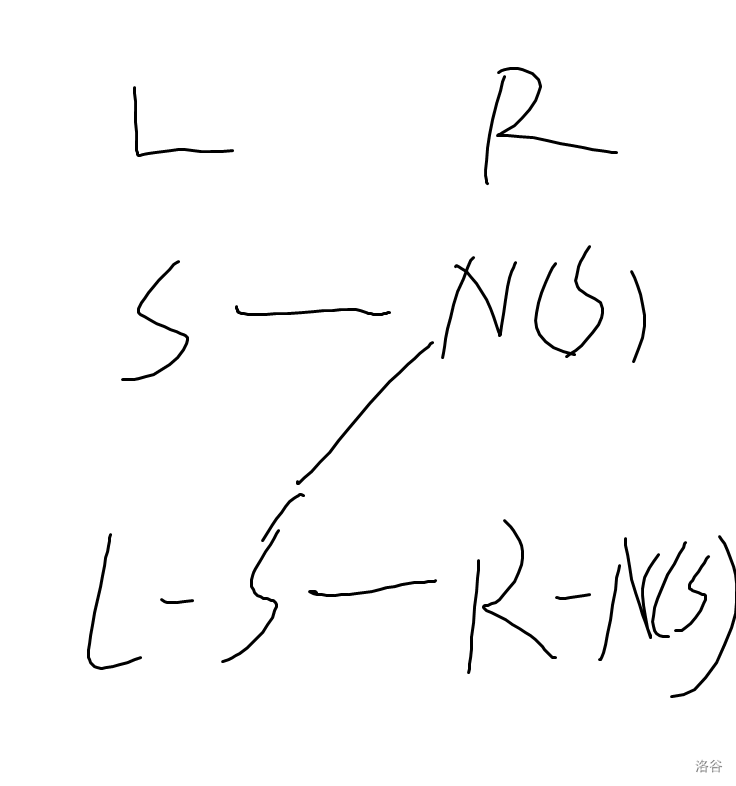
发现等价于求最小点覆盖。因为可视为枚举左部 不选而 选,那么 必选。
一般图完美匹配:Tutte定理
一般图有完美匹配当且仅当 且 ,其中 表示 构成的所有连通块中奇连通块个数。
推论:记 ,则最大匹配为 。
证明:我们将直接证明推论,考虑 为取到 最大值且点数最多的连通块,将其去掉后得到若干连通块 。
引理 1: 中不可能有奇连通块。
对于一个偶连通块,将其中任意一个点加入 后 至少加一,所以 不降,不符定义,矛盾。
引理 2:任意 去掉任意一点后它存在完美匹配。
记它为 。考虑归纳证明,只需证明 满足 Tutte 定理的条件。考虑 ,推一下式子勾连原图:
根据定义有 ,所以 。只要能证明左式为偶即可。分讨:
- :,故 。
- :同上 。
得证。
引理 3:将 视为左部点, 视为右部点,左部点存在完美匹配。
考虑 Hall 定理。考虑 构成的经典结构()。推式子找与 的联系,由于 的奇连通块被 包括了,放缩一下:
根据定义:
得证。
所以,只需按照引理 3 做完美匹配,那么由引理 2,被匹配的 的剩下的点也能有完美匹配。最后剩下一些无法匹配的只能扣掉一个点。显然是最优的。此时,剩下的未匹配点个数恰为 ,证毕。结合图像理解下:
最小割相关补充
对于任意一组割,记 分别为方案中与 连通的点集。
是最大流。关于等号为什么有,因为考虑其中一个流量,它会从 出发,从 走到 产生 贡献、反之 贡献。最终走到 所以恰为 贡献。
由此可知最小割的边必然满足满流。然后我们考虑一下此时残量网络的结构,首先最大流 所以 ,而且不存在增广路因此 不能到 。即缩点后为 的 DAG。
可行边判定:满流;同时残量网络中 不能走到 ,等价于 。
必经边判定:是可行边,且 。因为只可能 在 的 间才能做到改变它就改变最大流。
最小割方案:残量网络上令 所在 (也就是 能走到的点)为 ,其余为 。不难验证。
最小割常见模型
- 二元关系建图:有若干 变量,当 产生贡献等等。
- 分层图的割建图:可用于刻画覆盖所有转移路径等。例如 LIS。
- 最大权闭合子图:建超级源汇, 连向正权点、容量为点权,负权点连向 、容量为点权相反数,原图的边权均为 。构造方案考虑最小割,若 割了代表不取 、 割了代表取 。
- 最小割中割掉一点却可能代表取这个点,所以要灵活。
平面图割与对偶图路径的转化
首先由对偶图环对应平面图割集,不难想象。但这是不便利用的。
做如下构造:原图中,将 连边(一般来说画在原图很外面,可以画成几条无限延伸的射线),那么得到一个新的面,令它为对偶图上的起点 ,无限面为中终点 ,忽略刚才 连边对应的边。
则此时, 的简单路径对应平面图上 一组简单割(不存在点同时与 分隔),路径长度即为割边数量,所以平面图最小割对应对偶图最短路径。
证明容易,加上 连边(即 连边)后构成了环,环将 分开,便对应原来 割。
CF1178H Stock Exchange
第一问:股票的转换相对独立,考虑转换过程。一个重要的观察是,一只股票除 时刻和最后一次变换的时刻外产生的变换,都是不必要的。证明考虑 时刻往后 时刻第一次变换,记原来股票 、变成 ,那么 ,发现若 则 ,也就是价值更低不必换了。所以想到二分答案 ,由结论只会在 时刻变换,便能求出每只股票最终可得的股票为一个前缀,由 Hall 定理知判定条件为排序后 。。
第二问:网络流建模是容易的,只会产生两次变换,每次变换的建边可用前缀优化,边数线性了。
CF708D Incorrect Flow
考虑先不管 的限制,那么很像上下界流,只需建立超级源汇 ,若流进来的不够就向 连对应流量的边,反之同理。跑最大流即可。
接下来刻画 的限制和修改,除了 时 变大要花费 以外花费都是 ,分讨一下:
- : 先有 容量、花费 ,然后 容量、花费 。
- :无论如何必须花 代价使得 ,先提前计算。然后 有 容量花费 ,此后 容量 花费 , 容量 花费 。
对于边的最优修改显然不会又增又减的,所以上面这种对增减分开处理的方法是正确的。跑 MCMF 即可。
CF103E Buying Sets
子集视为左部点,元素视为右部点,子集向包含的元素连边。子集的并的大小不小于子集,即为满足 Hall 定理。
如何利用完美匹配来刻画子集数量恰为它的并?考虑最小权闭合子图,原来的边左往右连,并跑出来一组完美匹配让右往左连,答案即为最小权闭合子图。
证明:显然最小权闭合子图左右部点数相同;考虑某个合法方案中存在右部点满足其对应(完美匹配)的左部点没被选,那么它会被另一个左部点选,同时这个左部点本身也对应一个右部点,接下来容易发现左右部点数量不可能相同。
也存在补集转化最小割的构造方法。
P3488 [POI 2009] LYZ-Ice Skates
之前做过。建二分图,用 Hall 定理判定 ,那么假如两个人 满足 ,那么显然把 都选上更优。所以形如若干个 互不相交连续段,只需知道正负即可,所以只需考虑一个连续段的情况。维护个最大子段和即可。
启示:一些复杂问题,利用 Hall 定理转化再加上一些最优化分析,往往可以得到简洁优美的结构。
CF981F Round Marriage
显然二分答案,然后每个点匹配的是环上一段。破环成链。同上, 相交的话可以把中间的都取了,所以形如若干不相交的连续段,然后考虑一段即可。
P8484 「HGOI-1」Mole
考虑费用流建图, 连向地鼠,地鼠可以被打多次所以需要复制多个代表不同代价,由于代价递减所以一只地鼠不会出现非前缀的情况。然后地鼠连向对应的区间、区间再连向 :
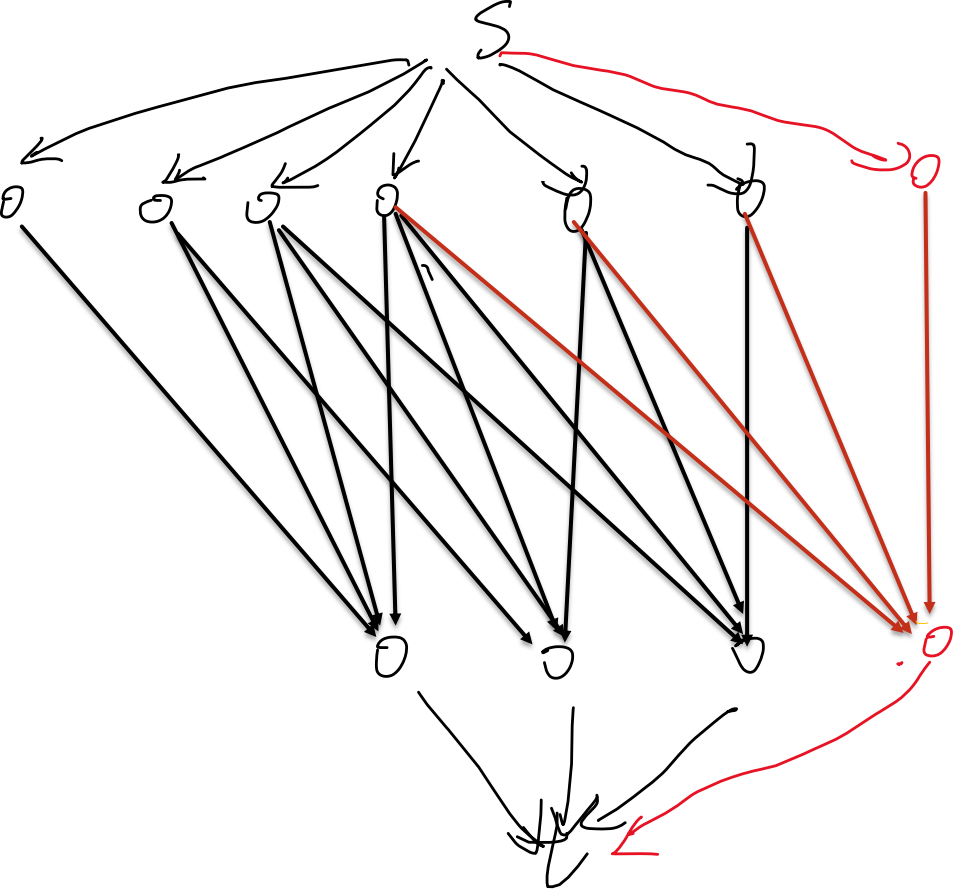
考虑滑动窗口,每次右边新增一个地鼠和区间。动态加点的情况下需依次考虑:消负环、跑增广。
考虑上述过程,注意到将一个区间向 的边退流是没有意义的,因为之后这条边也会满流。
接下来继续模拟费用流感觉没有前途,因为增广路形态太多了,回归原问题。但是根据上面的讨论,不会出现地鼠被锤的次数变少的情况。
每次找到可以被锤的地鼠中贡献最大的,锤他。刻画“可以被锤”,点对区间的形式联想到前面几题,利用 Hall 定理。记 为被锤次数,当前考虑到区间 ,合法当且仅当每个区间 满足 ,考虑分讨去掉 :
- 首先,假如 不妨直接取 、 不妨直接取 。
- :,由于 ,而 新来不可能 ,所以一定合法。
- :同上。
- :。
- :。
对于后两种,考虑这样的过程:将取等号的极大区间标记,每次取未被标记的最大 。
每次只需考虑 即可。不对啊?!之后要是 变化了就有可能出现原本 号变成 号。
事实证明,存在这样的 hack!群友找到了,群友神力!
fishpear:我没实现这个做法。
P9528 [JOISC 2022] 蚂蚁与方糖
运用 Hall 定理推论,求 。我们还想套用之前题面的套路,不过因为不是简单判定正负的原因,可能会选多个连续段。但是,这些连续段对应的 肯定不交。
没办法,考虑 dp,但是带修改,而矩阵优化也不现实,所以考虑放到权值线段树上。那么记 表示考虑连续段在 对应的区间 上,且对应的 的左端点(右端点)是否越过 ()。转移时假如是 才可能出现 相交的情况,由先前结论假如相交时左右拼起来还存在间隙,那么肯定不优,所以只需加上 (区间糖果数)即可。这个东西顺便维护一下即可。
考虑修改,假如是蚂蚁修改好做,逐次
push_up 更新 即可。但是糖果修改会对 的蚂蚁都产生修改,这相当于对动态 dp 做区间修改!真的能做吗?可以的兄弟,可以的。因为一般来说动态 dp 只能依靠
push_up 来更新,但是本题的问题相对简单可以计算影响。对于 是容易的,因为 内的区间,只要选了蚂蚁这些糖果就会被计入 中,所以 ,打个标记即可。
不过对于 需对节点可能的影响进行分讨。能影响等价于 ,那么 内的区间都会 打个标记就好;而拆出来的 个区间的祖先也可能被影响,在
push_up 前处理一下即可。细节:一般线段树 ,所以上面的也可以看作 可以与 一起处理。。
启示:这题的转化很典,这种左部点对应一个定长区间的问题一般转化为若干 不交连续段。后面的动态 dp 也不难想(可能就转移对中间相交的处理有点难),但是对动态 dp 区间修改太神了,完全没见过。所以不要先入为主地误认某些问题不可做。
AT_arc190_e [ARC190E] Gaps of 1 or 2
考虑建模,考虑 列第 列有 个数,距离 的两列的点都有连边,求最大匹配。
考虑 Tutte 定理,选个 ,最大化 。
考虑无用情况。发现对于一列,若选了点但是不全选非常亏,因为考虑一列选的点逐渐变多但是不选完,那么连通块个数不会变化只是说有一个连通块奇偶性变化。可是 稳定 ,显然是亏的。
于是一列要么全选要么不选,已经可以 dp 了。有剪枝,注意到 即一列选但相邻都不选是亏的,因为相邻两列还是可以跨过它连边,那不选这列不劣。于是,存在最优解满足没有跨过一列的边,连通块必然是 连续段,减少了状态数以及转移难度。
只需 种状态,然后矩阵乘法做区间查询即可。注意 不会被最优性过滤,需手动判定。
启示:一般图的最大匹配可以用 Tutte 定理转化,这东西第一次见捏。
P3308 [SDOI2014] LIS
LIS 问题有关的一般考虑按 dp 值分层。利用这个建出分层图,相邻层有连边,再让 连向第一层、最后一层连向 ,那么一个 LIS 对应一条 路径。那么就要割掉一些点使得不存在路径,所以点拆为边跑最小割即可。
字典序很难直接刻画,考虑按 从 到 看看能不能割掉。相当于是最小割中的可行边,如果是才把它割掉,之后重新跑一遍最小割,以此类推。
启示:这题是典型的分层图最小割建图,并运用可行边相关知识。
P3756 [CQOI2017] 老C的方块
观察:所有情况形如一个蓝边两边分别放置一个 的矩形,且这恰为所有情况。
矩形可用连边刻画,只需让相邻点连边即可。由此我们得知本题大概框架:建分层图跑最小割。本题应分为 层,每层向下一层有边。
考虑染色代表层数,考虑如何染色(建议画图):
- 相邻格子必然是相邻颜色。
- 考虑“田”与“L”型,那么它们有三个格子是共用的,则第四个格子颜色相同。即每条竖线右侧与右下方颜色相同。
- 考虑“一”型,可知水平方向上四个相邻格子颜色互不相同。
由此便能推出四列的染色方案:
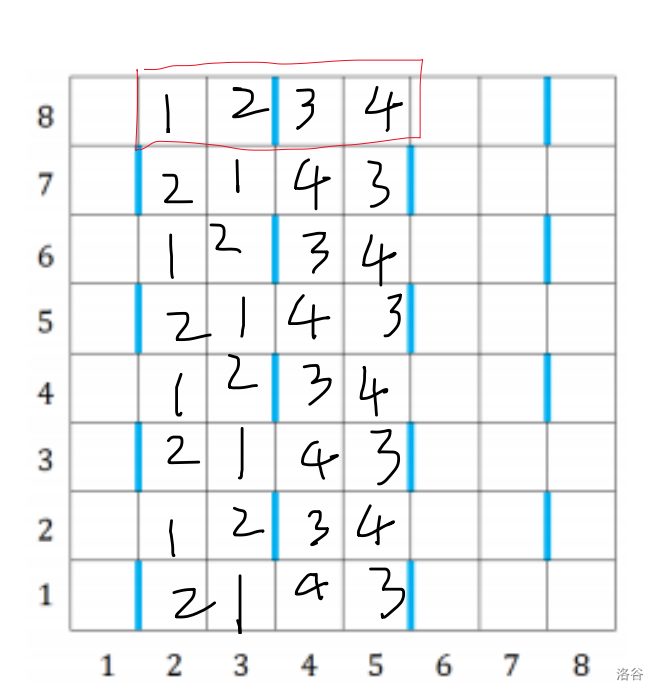
拓展两列也是容易的,相当于沿着边线水平翻转一次即可,那就做完了。
启示:感觉本题不难,联想到形如两个矩形通过蓝边连接后,再手玩几下就没了。但更理性一些的思考应为:分层图路径刻画非法 pattern、构造染色方案、观察特点减少枚举量。
TCO13 Semifinal2 OneBlack
题意:有一个 的网格,每个点可能是障碍和空地,求将空地黑白染色的方案,使得任意左上到右下的路径(向下或向右),经过恰好一个黑色格子。。
原题做法为 dp 套 dp,状态优化后才能过。事实上可以 。
考虑用割刻画,染黑视为割掉一个点。首先点转边,然后向右向下连边。左上入点、右下出点为源汇,一个简单割集(任意点与 至少一点连通)能够保证恰好经过一个黑色格子,考虑路径对应一个流量,本题建模不带环,故它恰有一次从 集到 集的转变。
考虑平面图割转对偶图路径。形如下图:
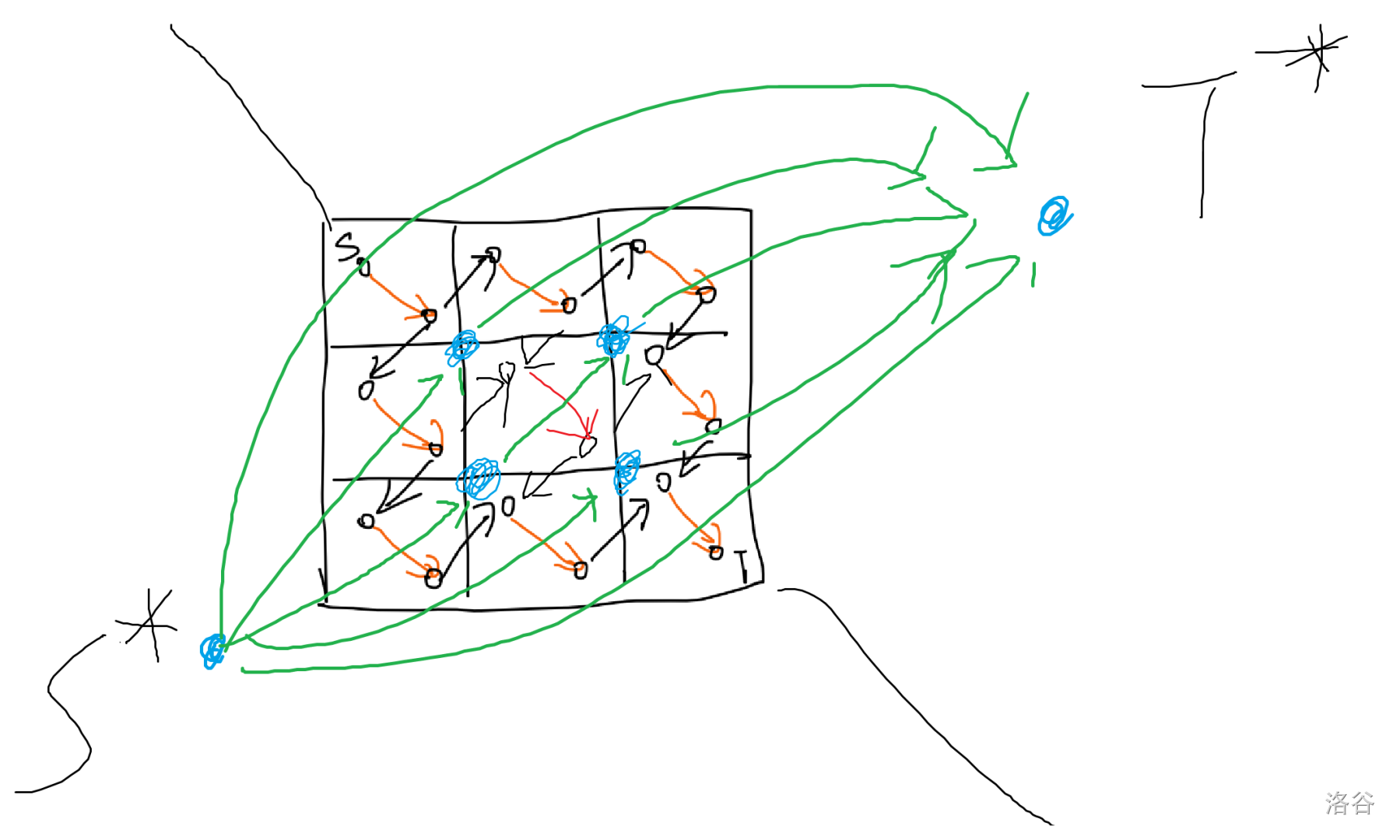
那么对偶图中,点为格子四个顶点,每个格子左下到右上有连边,边界除外。而障碍物相当于删掉一个点向外界的连边,最终会构成若干连通块,所以可视为将四个角的点合并。并查集维护即可。,瓶颈为并查集。
注意特殊情况,上面默认建模出来个连通图,但可能存在空地但是不被任意路径经过,将其视为障碍,答案 即可。
AT_arc106_e [ARC106E] Medals
做过,二分答案,然后最link小割或者 Hall 定理都行,最后 sosdp。
AT_abc332_g [ABC332G] Not Too Many Balls
建模按题意模拟即可。最大流转最小割,这个图结构简单就上下两排,可以考虑直接计算割集。枚举 为球这一排与 连通的, 为箱子这一排与 连通的,答案为:
为二元项加一元项,难以直接计算。 较小,考虑枚举 ,那么 背包即可, 有关项发现等价于 ,相当于分段函数(每个只有两段)叠加,差分维护一下即可。
CF1919F2 Wine Factory (Hard Version)
相当于求下图最大流:
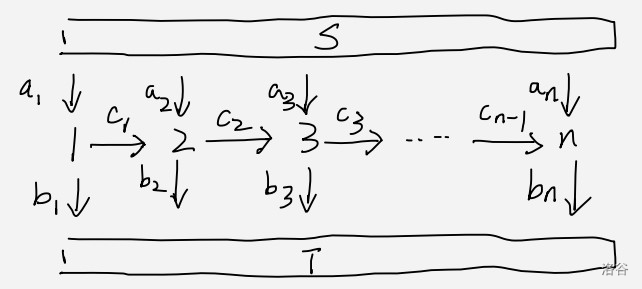
转最小割。枚举每个点属于 集,为 ,那么 分别产生 代价,同时相邻 会产生 代价。
又看到单点修改,想到放线段树上 dp。记 为 代表的区间左右为 即可。
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...