专栏文章

题解：P1001 A+B Problem

wwwwidk1234
P1001题解参与者 29已保存评论 29

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
29 条
当前快照
1 份
快照标识符
@mipcyypc
此快照首次捕获于
2025/12/03 09:58
3 个月前
此快照最后确认于
2025/12/03 09:58
3 个月前
查看原文

题目

给定两个整数 a,ba,b，求 aa 与 bb 的和。

思路

本题有多种解法，充分发挥一题多解的思维可以更好地提升 OI 能力。

思路 1

我们首先定义两个变量 a,ba,b：int a,b;。在 C++ 中，int 为整形变量，可存放 −231∼231−1-2^{31} \sim 2^{31}-1 之间的整数。
接着使用 cin>>a>>b; 语句读入 aa 与 bb 的值。输入数据中 a,ba,b 之间用一个空格隔开，所以 cin 就会将第一个数赋值给 aa，第二个数赋值给 bb。
然后使用 cout<<a+b; 语句输出 aa 与 bb 的和。cout 的功能是输出变量、字符串、常数等值。如果你想在输出后加上一个换行，那么可以使用 endl，比如 cout<<a<<endl<<b;，这句话的意思就是将 a,ba,b 分别在两行中输出。
注意，cin 和 cout 功能都在 iostream 头文件中，如果想使用就必须将头文件导入。使用 #include<iostream> 语句即可将 iostream 导入。在更深入学习信息学编程之后将会用到更多的功能（比如 queue 等），如果想使用就必须将每个功能的头文件分别导入。如果不想记忆的话，可以使用 #include<bits/stdc++.h> 将所有头文件导入。同时，cin 和 cout 等也必须使用 using namespace std; 将命名空间引入。
参考代码：
CPP
#include<bits/stdc++.h>
using namespace std;
int main()
{
	int a,b;
	cin>>a>>b;
	cout<<a+b;
	return 0;
}

思路 2

看到题目中的 a,ba,b 并求它们的和，可以联想到区间求和问题，用树状数组维护一个长度为 22 的序列 cc，首先对 c1c_1 增加 aa，然后对 c2c_2 增加 bb，接着使用 query 函数将 c1∼c2c_1 \sim c_2 的和求出即为答案。
参考代码：
CPP
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=5;
int a[N],c[N],n,Q;
inline int lowbit(int x)
{
	return x&-x;
}
inline void modify(int x,int v)
{
	for(int i=x;i<=n;i+=lowbit(i)) c[i]+=v;
}
inline int query(int x)
{
	int s=0;
	for(int i=x;i;i-=lowbit(i)) s+=c[i];
	return s;
}
int main()
{
    n=2;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        modify(i,a[i]);
    }
    cout<<query(2);
    return 0;
}

思路 3

考虑使用最短路算法。首先考虑一个三个结点三个边的有向图，如下所示（其中 11 到 33 的边权为一个很大的数，比 a+ba+b 的值大）：
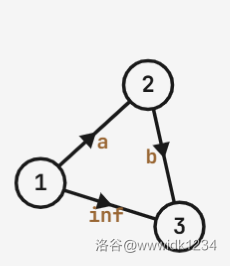
最短路径就是 1→2→31 \to 2 \to 3，所以求 a+ba+b 的值就等同于求 11 到 33 的最短路径。因为只有三个结点，所以考虑 Floyd 算法。
参考代码：
CPP
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr ll inf=1.2e18;
constexpr ll N=7;
ll g[N][N];
int main()
{
    memset(g,0x3f,sizeof g);
    int n=3;
	cin>>g[1][2];
	cin>>g[2][3];
	g[1][3]=inf;
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
	cout<<g[1][3];
	return 0;
}

思路 4

二项式定理：对于任意自然数 nn 以及实数 a,ba,b，均有：
(a+b)n=∑k=0nCnk⋅an−kbk(a + b)^n = \sum_{k=0}^n C_n^k \cdot a^{n-k} b^k
题目可转化为求 (a+b) mod p(a+b) \bmod p 的值，其中 p=1218000211019p=1218000211019 为质数。所以我们可以考虑使用二项式定理求解该题目。
其中 CnkC_n^k 为组合数，计算公式如下（x′x ^{\prime} 表示 xx 在模 pp 意义下的逆元，根据费马小定理可以计算出 x′=xp−2x ^{\prime}=x^{p-2}）：
Cnk mod p=n!k!(n−k)! mod p=n!⋅k!′⋅(n−k)!′ mod p\begin{aligned} C_n^k \bmod p &= \dfrac{n!}{k!(n-k)!} \bmod p \\ &= n! \cdot k!^{\prime} \cdot (n-k)!^{\prime} \bmod p \end{aligned}
首先初始化一下阶乘和阶乘的逆元（f[i] 表示 ii 的阶乘，invf[i] 表示 i!i! 的逆元，ksm(a,b) 的功能是计算 ab mod pa^b \bmod p 的值）：
CPP
f[0]=invf[0]=1;
for(int i=1;i<10;i++) f[i]=f[i-1]*i%mod;
for(int i=1;i<10;i++) invf[i]=invf[i-1]*ksm(i,mod-2)%mod;
然后套二项式定理公式：
CPP
ll ans=0;
for(int k=0;k<=1;k++) ans=(ans+C(n,k)*ksm(a,n-k)*ksm(b,k))%mod;
最后输出 ans 即可。
参考代码：
CPP
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=10;
constexpr ll mod=1218000211019;
ll a,b,f[N],invf[N];
inline ll ksm(ll a,ll b)
{
    ll s=1;
    while(b)
    {
        if(b&1) s=s*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return s;
}
inline ll C(ll a,ll b)
{
    if(a<b) return 0;
    return f[a]*invf[b]%mod*invf[a-b]%mod;
}
int main()
{
    cin>>a>>b;
    int n=1;
    f[0]=invf[0]=1;
    for(int i=1;i<10;i++) f[i]=f[i-1]*i%mod;
    for(int i=1;i<10;i++) invf[i]=invf[i-1]*ksm(i,mod-2)%mod;
    ll ans=0;
    for(int k=0;k<=1;k++) ans=(ans+C(n,k)*ksm(a,n-k)*ksm(b,k))%mod;
    cout<<ans;
    return 0;
}

评论

共 29 条评论，欢迎与作者交流。

正在加载评论...