专栏文章

数列分块入门 1

SStarsIntoSea
P13976题解参与者 15已保存评论 14

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
14 条
当前快照
1 份
快照标识符
@minz8v5u
此快照首次捕获于
2025/12/02 10:46
3 个月前
此快照最后确认于
2025/12/02 10:46
3 个月前
查看原文
建议学分块前先学会线段树。
简单说一下小的对分块的理解。
一般来说“分块”狭义上通常是指“块状数组”和“数列分块”（其实是一个东西），广义上是一种思想，比如根号分治和整除分块。下面说的“分块”都指狭义上的。
分块虽然在 NOI 大纲中是 8 级考点，但是并不难学。分块对比线段树的优势在于分块比线段树更加直观，扩展性更强，缺点就是时间复杂度略高，是 N\sqrt N 的。
因为分块的思想就是对某一个维护的东西进行划分，每一次操作都一定包括这些划分的东西，如果每次操作能够覆盖某个完整的划分，就可以“整体”操作。
说清楚点，比如给你一个数组：
然后对这个数组划分一下：
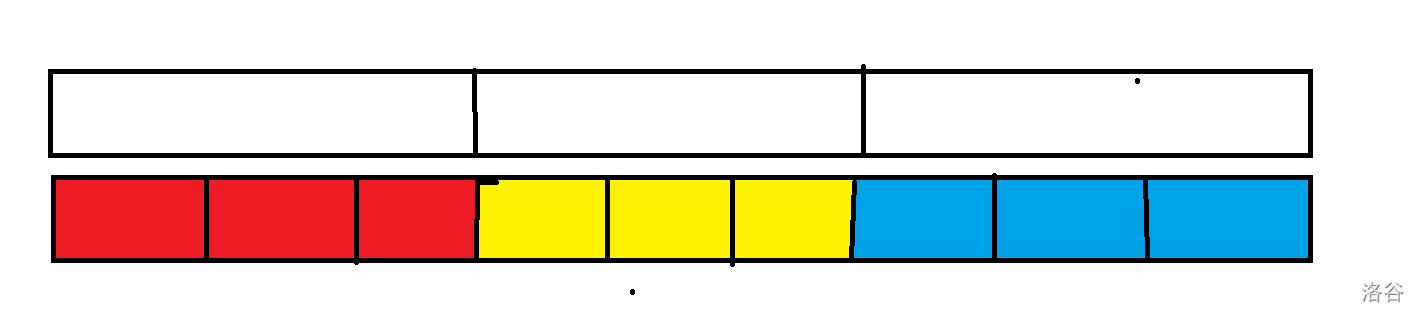
我们发现，每一个划分的区域要均匀，即每一个划分的区域长度要尽可能相等。就称每一个划分的区域为大块，原数组称为小块，划分的区域长度称为块长。这三个东西基本算是分块的三要素了。
比如红色的三个小块组成一个大块，黄的三个小块组成另一个大块。块长为 3。
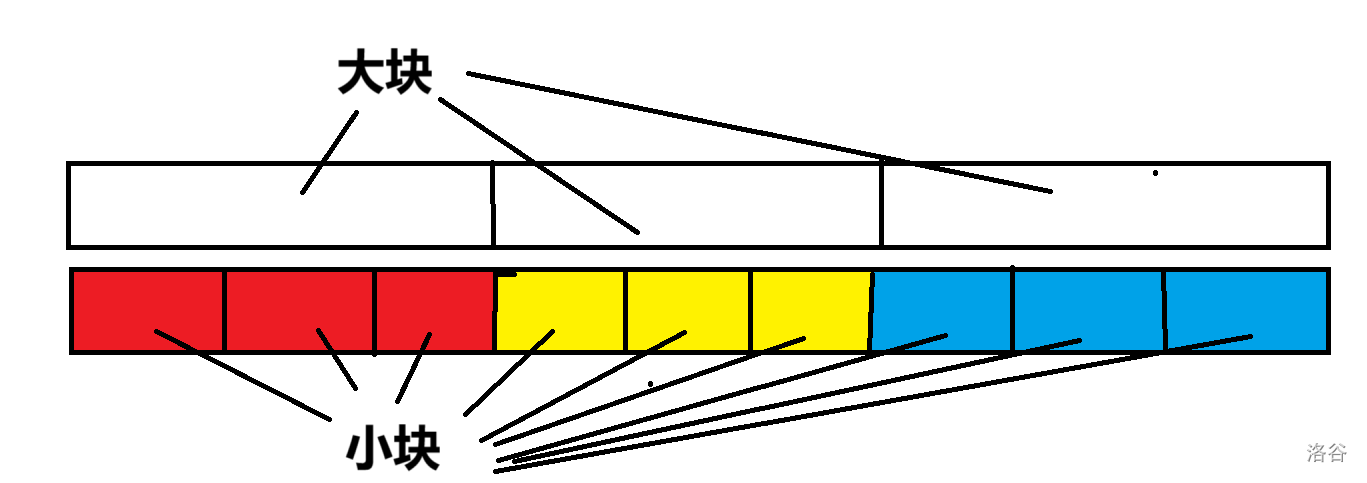
要求每个小块必须对应且只对应一个大块（即两个大块没有重叠的部分，且所有大块全部覆盖每一个小块）。
确定大块的过程称为建块，和线段树的建树类似。
代码：
CPP
int L[N],R[N],pos[N],cnt,B;
//L[i]表示第i个大块对应的最左边的小块
//R[i]表示第i个大块对应的最右边的小块
//pos[i]表示第i个小块对于哪个大块
//cnt表示有多少个大块
//B表示块长
void build(){
	B=sqrt(n); //块长通常为sqrt(n)
	while(1){
		++cnt;  //确定每一个大块
		L[cnt]=(cnt-1)*B+1;
		R[cnt]=cnt*B; //确定左右端点可以手推一下
		if(R[cnt]>=n){ //如果超了就判掉
			R[cnt]=n;
			break;     //最右边到头了就不必要往下找了
		}
	}
	
	//找每一个小块对应的大块
	for(int i=1;i<=cnt;++i) //枚举大块
		for(int j=L[i];j<=R[i];++j) //枚举每个大块包含的小块
			pos[j]=i;
}

//其实pos可以不用处理能直接根据块长算出来，L和R也可以根据块长算出来。建块的代码完全可以不写，在后面需要的时候直接算出来。但还是建议初学者用数组表示，避免错误。
代码中提到“块长”通常是 N\sqrt N。因为块长是 N\sqrt N，所以大块的数量也是 N\sqrt N。确定每一个大块是 N\sqrt N 的，找每一个小块对应的大块是 NN，所以建块的代码时间复杂度就是 O(N)O(N)。
说修改操作，比如 l=2,r=7l=2,r=7：
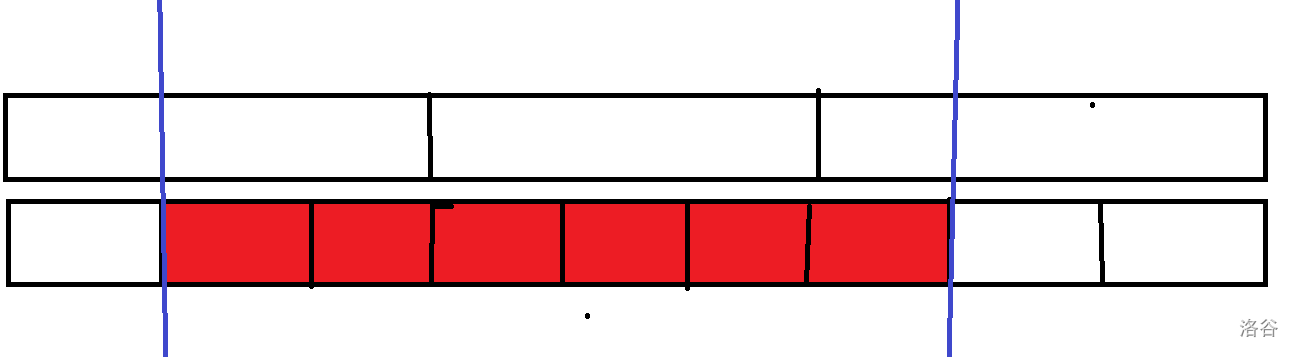
暴力的复杂度肯定是 O(N)O(N) 的，但是区间操作大概率会完整地包含某些大块，修改操作的左右两个端点可能不完整。
左右两个端点位置大概率不包含完整的大块，通常称这些没有被完全包含的小块称为散块，被完整包含的是整块。
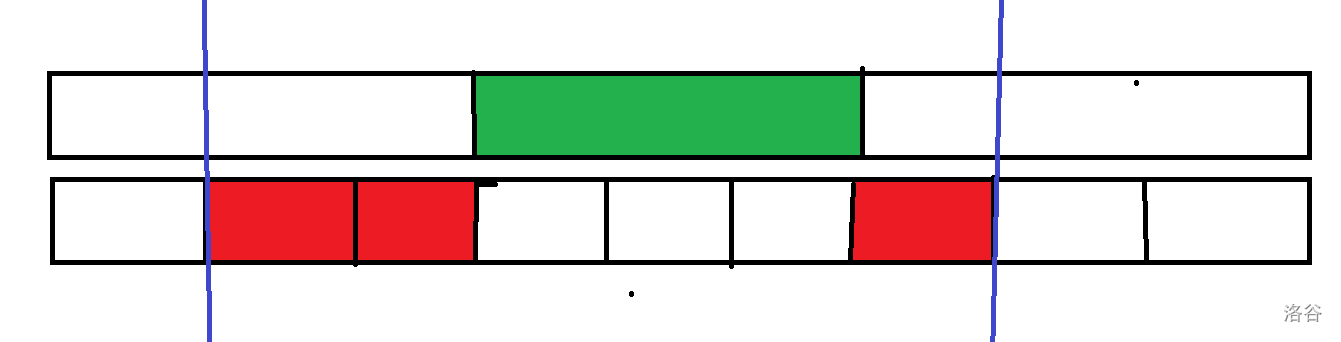
比如绿的就是整块，红的就是散块。
整块一定是大块，散块一定是小块。
块长是 N\sqrt N，那么左边散块的数量一定不超过 N\sqrt N 个，如果超过 N\sqrt N 个那么就有整块了。右边同理。所以散块的数量一定不超过 2N2\sqrt N，也就是 N\sqrt N 级别。因此，这些散块就可以直接暴力更新，复杂度 O(N)O(\sqrt N)。
整块的数量也一定少于 N\sqrt N 个，因为最多只有 N\sqrt N 个大块。但是这些整块该怎么修改呢？很简单，把线段树的懒标记思想引用过来，给每一个整块打上标记。需要查询的时候，直接是原数 + 对应大块的懒标记就行了。
这样处理散块和处理整块复杂度都是 O(N)O(\sqrt N)。
CPP
int tag[N]; //大块的懒标记
void update(int l,int r,int x){
	if(pos[l]==pos[r]){
		//如果在同一个大块就可以无脑暴力，因为最多只有sqrt(n)个小块
    //大部分情况下这里的操作是不能省略的，因为后面的操作会导致错误
		for(int i=l;i<=r;++i) a[i]+=x;
		return ;
	}
	for(int i=l;i<=R[pos[l]];++i) a[i]+=x; //左边的散块
	for(int i=L[pos[r]];i<=r;++i) a[i]+=x; //右边的散块
	for(int i=pos[l]+1;i<pos[r];++i) tag[i]+=x; //整块的懒标记
}
int query(int x){
	return a[x]+tag[pos[x]]; //原数+懒标记
}
懒标记没有必要下放，否则常数直接上天。
这时候就有人说了，唉？这东西感觉比线段树还麻烦，还要线段树的思想，复杂度还高，那还学什么分块？
分块解决的问题复杂多样，这只是用于学习分块的题。很多题线段树做不了但是分块能做，就在于分块扩展性极强。
等后面接触分块难题常有听到“调块长”这一词，就是修改块长，因为后面维护的信息多了，难免有的操作会有较大常数。因此，块长不能死板就是 N\sqrt N，要根据题目情况调节，找到尽可能跑的快的块长。有些题也会根据题目的实际需求确定块长。
如果你刚学分块，无论是学习还是写代码，都要弄清楚哪些是大块、哪些是小块、大块要干什么（维护什么信息），不然很容易晕，也不容易写好代码。
没什么可说的了，小的太菜还是少说最好。

评论

共 14 条评论，欢迎与作者交流。

正在加载评论...