Trick合集

放宽限制

很经典的Trick，当题目的限制难以计算和维护时，考虑是否存在一种更平凡的维护条件，而能使得题目的限制在这种条件下自然称为最优解。

差分贡献

形态1：类似

a_i=k

提供

k

贡献转化为对每个

i

，使所有

a_i \geq i

提供

1

的贡献。

形态2：对每个最终结果为

pos

的求贡献，转化为对每个最终结果

\le pos

的求贡献。

组合意义

适用于有多项式贡献

\rightarrow

的情况，分幂维护或组合意义，将一些有组合意义的式子转化为其组合意义，并进行dp。

分数计算

当题目要求输出分数，但分数的分子分母在运算中可能变得很大时：

1.找一个大于答案的质数p，将分数对p取模得到c，之后再一个个尝试分母b，根据a=cb（modp）来还原分数。

2.直接使用python的分数类型

dsu on tree

对一颗树上的信息统计，若能做到O(1)的加入数据和O(1)的删除数据，则可以使用dsu on tree

核心要点是树链，然后用一个数组统计，对于每个点每次先遍历所有轻儿子，每遍历一个轻儿子之后将该儿子子树数据删除，最后遍历重儿子，重儿子遍历出来后数据不删除，加上所有轻儿子子树的数据再加上该点本身的数据作为该点的数据。

其复杂度很好证明，每个点除开第一次被统计，只会额外在祖先链上的每条轻边被删除一次再被统计一次，而祖先链上的轻边不超过log条，所以复杂度为

O(nlogn)

CF600E Lomsat gelral

CPP

#include<bits/stdc++.h>
#define N 100010
#define pb push_back
#define int long long
using namespace std;
int n,a[N],buc[N],siz[N],son[N],mx,ans[N],mxs;
vector<int> to[N];
void dfs0(int now,int fa) {
	siz[now]=1,son[now]=0;
	for(int v:to[now]) if(v!=fa) {
		dfs0(v,now),siz[now]+=siz[v];
		if(siz[v]>siz[son[now]]) son[now]=v;
	}
}
vector<int> id;
void add(int x) {buc[x]++; if(buc[x]==mx) mxs+=x; if(buc[x]>mx) mx=buc[x],mxs=x;}
void dfs2(int now,int fa) {
	add(a[now]),id.pb(now);
	for(int v:to[now]) if(v!=fa) dfs2(v,now);
}c
void dfs1(int now,int fa) {
	for(int v:to[now]) if(v!=fa&&v!=son[now]) {
		dfs1(v,now);
		for(int x:id) buc[a[x]]=0;mx=mxs=0;id.clear();
	}  
	if(son[now]) dfs1(son[now],now);
	add(a[now]),id.pb(now);
	for(int v:to[now]) if(v!=fa&&v!=son[now]) dfs2(v,now);
	ans[now]=mxs;
}
main() {
	cin.tie(0)->sync_with_stdio(0);
	cin>>n;
	for(int i=1; i<=n; i++) cin>>a[i];
	for(int i=1; i<n; i++) {
		int u,v;cin>>u>>v;
		to[u].pb(v),to[v].pb(u);
	}
	dfs0(1,0),dfs1(1,0);
	for(int i=1; i<=n; i++) printf("%lld ",ans[i]);
}

决策单调性

决策单调性表现为对于

i>j

则

f_i

的决策点

p_i>p_j

。

决策单调性需要性质：相交优于包含，这条称作四边形不等式。

以最大贡献为例，即对于任意的

a<b<c<d

有

w(a,d)+w(b,c)\le w(a,c)+w(b,d)

其与

w(a,b+1)+w(a+1,b) \le w(a,b)+w(a+1,b+1)

等价，证明容易，不必记。

若

f_i

不需要之前的

f_j (j<i)

来贡献，则可以使用分治法，初始设

(l,r,L,R)

表示目前待确定的为

f_{l-r}

，其决策点属于区间

(L,R)

。

每次找出

(l,r)

的中点

mid

的决策点后分治即可。

其二是单调队列法，考虑记三元组

(p_i,l,r)

表示决策点

p_i

目前为

l,r

范围内的最优解。队列里从头到尾

l,r

逐渐增大。当

f_{i+1}

需要贡献时，我们从头开始排除

r<i+1

的三元组，之后将队首作为答案当我们加入一个新的值

i+1

之时，我们从队尾开始往前，如果

w(i+1,l)>w(p_i,l)

说明该决策点完全不如

i+1

，将其排除，否则在

(l,r)

内二分一个

i+1

优于

p_i

的分界点

x

，将原本的

(p_i,l,r)

改为

(p_i,l,x)

并在队列末尾加上

(i+1,x+1,n)

。

例题：P3515 [POI 2011] Lightning Conductor

prufer序列相关

定义：在一棵无根树中，每次删除最小的叶子并将叶子相连点编号加入序列。

性质：prufer序列与无根树一一对应

性质：大小为

n

的无根树的数量有

n^{n-2}

种，这同时也是完全图生成树的数量。

性质：每个结点在序列中出现的次数是其度数减一

建构：用一个指针维护目前最小的叶子，可以发现如果新出现的叶子比指针维护的叶子小，那么其可能出现的新的最小叶子为一根链，边跳边进序列即可，每个点最多被遍历两遍，复杂度

O(n)

。

CPP

void solve1() {
	for (int i = 1; i <= n - 1; i++) cin >> fa[i], deg[fa[i]]++;
	for (int i = 1, p = 1; i <= n - 2; i++, p++) {
		while (deg[p]) p++; // 自增找到下一个叶子结点
		pf[i] = fa[p]; // 加入序列
		while (i <= n - 2 && --deg[pf[i]] == 0 && pf[i] < p) // 如果产生新叶子结点且编号更小
			pf[i + 1] = fa[pf[i]], i++;
	}
}

还原：过程类似，不多赘述。

prufer序列还有很有趣的用途（来自oi-wiki）：

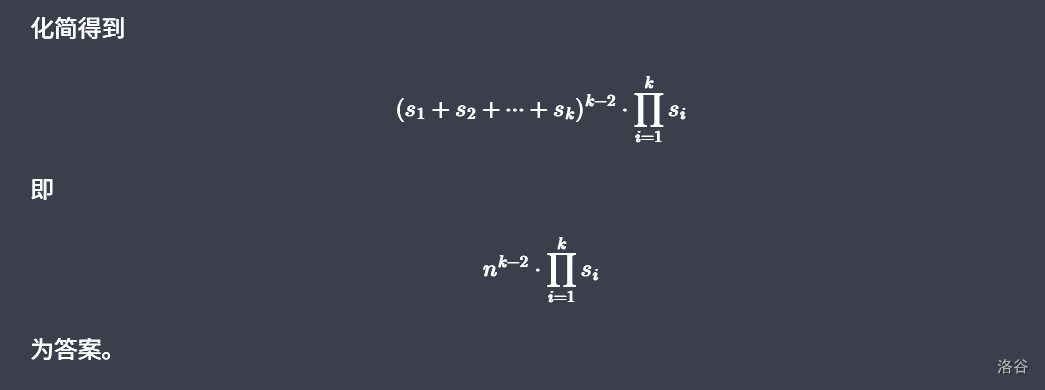
至于那个多元二项式定理，脑内展开一下

(x_1+...+x_m)^p

即可得到。

一类kth-element问题

给出大小为 $n$ 的可重集 $S=\{a_1,a_2,...,a_n \}$ ，按顺序输出子集和前 $k$ 小的子集的子集合。 $n,k\le 5\times10^5$

首先将负数全加进答案，然后将负数取反，此时取一个负数的相反数相当于不取这个数，我们就将问题归纳到了全非负的情况。

排序。考虑在全非负的情况下，除去全不选的状况，最小的肯定是选

a_1

。我们用一个集合来维护，每次弹出最小的方案，将其输出，然后我们把它的两个后续方案：该方案加上该方案中最大数的下一个数，或该方案减去该方案中最大数后加上该方案中最大数的下一个数。一直操作直到输出前

k

大的方案即可。

为什么是对的呢？显然对任意一个非起始状态的状态而言，它都有一个唯一的前驱，且这个前驱一定小于它，假设我们已经输出了前

i

小的状态，此时第

i+1

小的状态一定在前

i

小的状态里面，即第

i+1

小的状态一定在堆里面，因此我们一定能将其扩展到。

我们放宽条件，考虑这一类 kth-element 问题，这类问题的共同特点是总方案数很大，但需要求的数的位置较为靠前。此时我们只要能构造出一种扩展方案，使得每个状态的至少一个前驱状态比它小，那么我们就能通过一个堆来维护。

Slope trick

slope trick 是一类用于维护下凸的dp函数的技巧（通常是下凸的分段一次函数）。如同所有的技巧一般，slope trick也有自己鲜明的特征，先来看一道例题。

CF713C Sonya and Problem Wihtout a Legend

给定一个有 $n$ 个正整数的数组，一次操作中，可以把任意一个元素加一或减一。（元素可被减至负数或 $0$ ），求使得原序列严格递增的求最小操作次数。

我们设

f_{i,j}

表示考虑到第

i

个数，它最终改变为

j

的最小操作数。

很容易列出转移式子：

f_{i,j}=\min \limits_{k=1}^{k<j}f_{i-1,k}+|a_i-j|

看到转移柿子里存在绝对值函数，考虑用 slope trick 维护。先简单用数学归纳法证明下

f_i

是个下凸函数。

假设

f_{i-1}

长这样：

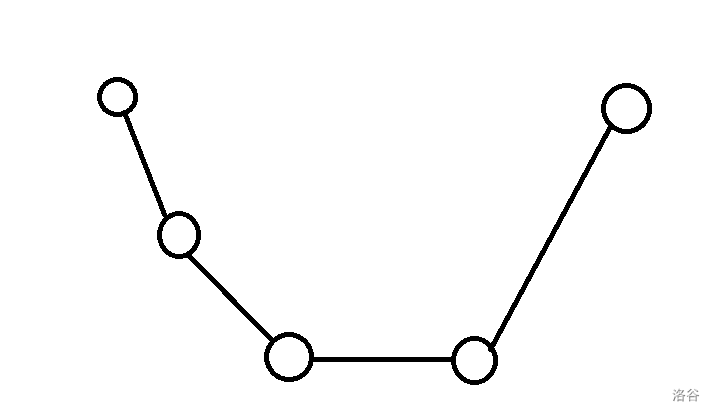
取 min 之后长这样：

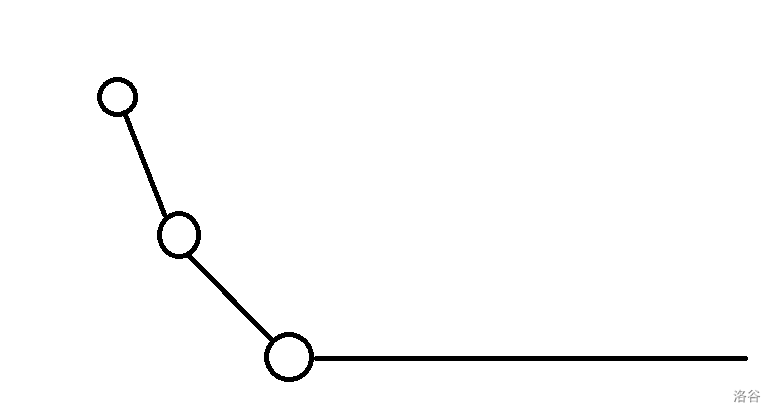
绝对值函数也是下凸函数，显然两个下凸函数加在一起还是下凸函数。

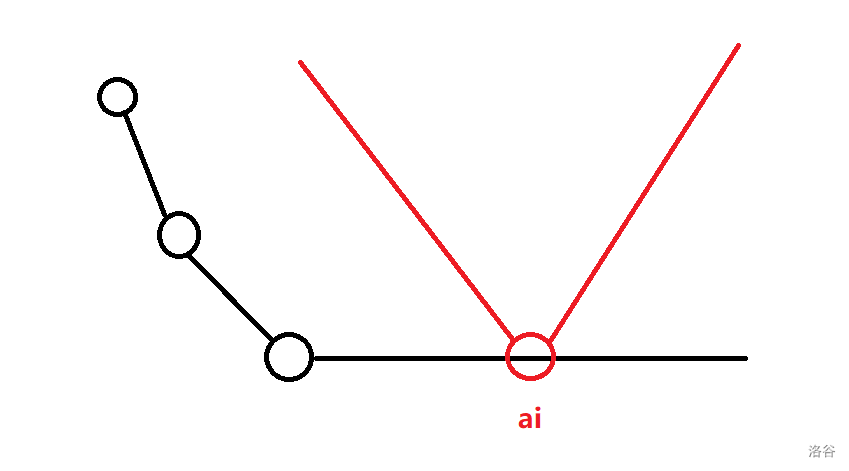
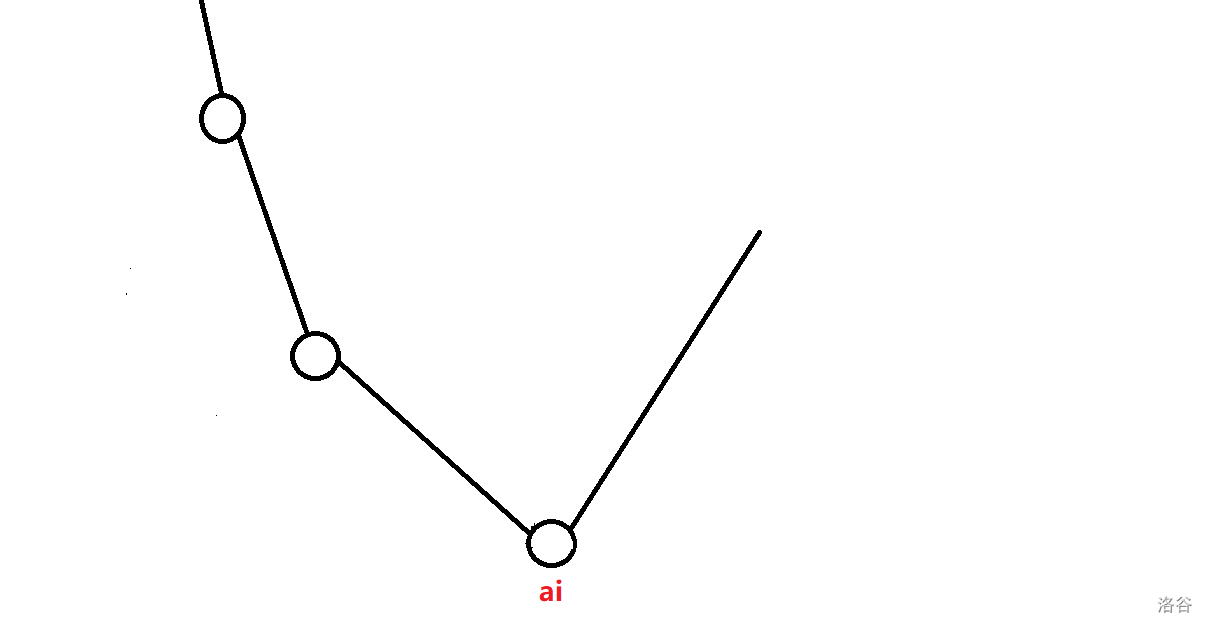
函数上有很多分界点，函数在经过分界点的时候斜率会加一，因此我们可以通过维护分界点来维护整个函数。

回到这一题，我们考虑使用一个大根堆来维护所有分界点，其中堆顶是当前 dp 函数的最低点（最低点右边的分界点在每次 dp 转移的时候都将被删除，因此没必要维护）。

现在考虑加一个绝对值函数

|a_i-j|

，显然

a_i

左边的部分斜率减一，右边的部分斜率加一，分两种情况讨论：

$a_i$ 在当前最低点的右边，此时最低点右移到 $a_i$ 的位置，而最低点对应的 dp 值不变，并将一个 $a_i$ 放进堆中（左边的斜率减一，右边的斜率虽然加一但在之后的转移中会被推平，因此斜率变化从负一到零，加入一个 $a_i$ ）。
$a_i$ 在当前最低点的左边，假设当前最低点为 $x$ ，先将两个 $a_i$ 放进堆中，此时最低点左移至堆中次大值的位置，最低点对应的 dp 值将会加上 $x-a_i$ （此时 $a_i$ 左边斜率减一而右边斜率加一，斜率变化从负一到一，因此加入两个 $a_i$ ）。

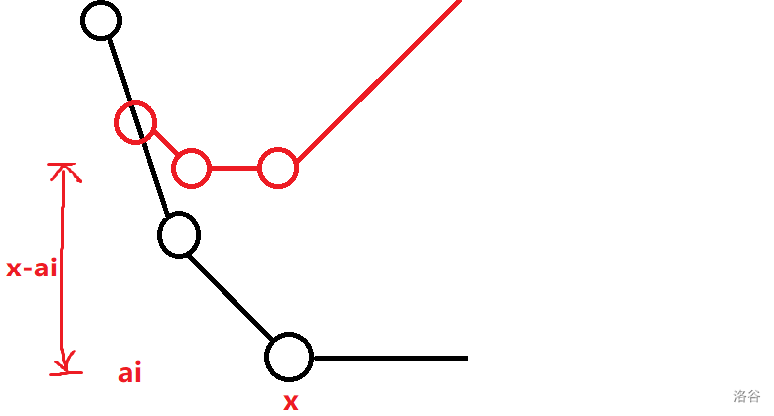
代码也及其好写：

CPP

#include<bits/stdc++.h>
#define int long long
using namespace std;
priority_queue<int> q;
int read() {
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
	return f*res;
}
int n,ans;
signed main()
{
	n=read();
	for(int i=1; i<=n; i++) {
		int tmp=read()-i;
		q.push(tmp);
		if(tmp<q.top()) {
			ans+=q.top()-tmp;
			q.pop();
		}
	}
	printf("%lld",ans);
	return 0;
}

一类集合计数问题

一类集合计数问题，形如

给定一个数列 $A$ ，设一个集合 $S=$ $\{$ $a_{b_1},a_{b_2},a_{b_3},\dots ,a_{b_k}$ $\}$ ，其权值为 $val(S)$ ，求所有满足集合内所有元素进行⊕运算后值为 $x$ 的集合的权值和。

其中 ⊕ 运算是任意位运算，

val(S)

是某种能用多项式表达出来的函数。

这种问题我们可以用 FWT 来解决。以

val(S)=1

为例，显然我们可以将原式表达成集合幂级数形式：

\prod \limits_{i=1}^n (1+x^{a_i})

这里的乘是 ⊕ 运算。

显然直接 FWT 是不可行的。我们对每个因式考虑他的 FWT。由于因式只有两项，所以其对 FWT 每一位的贡献只有两种可能，我们设其为

p

和

q

。

这里运用到一个性质，FWT 的和等于和的 FWT，我们将所有因式加在一起进行 FWT。考虑 FWT 后第

i

位的值为

c_i

，显然可以列出式子

kp+(n-k)q=c_i

,解完式子之后我们就可以知道这一位有多少个

p

，多少个

q

，我们变可以依此推出 FWT 的乘积在这一位为

p^k q^{n-k}

。

典例1：

给出 $m$ 个长度为 $n$ 的 01 数列（每个 01 数列表示一个集合），求选出一些使其并集为 $S$ 的方案数。

或卷积，每个因式对每一位的贡献为

1

或

2

，解方程即可。

典例2：#310. 【UNR #2】黎明前的巧克力

异或卷积，每个因式对每一位的贡献为

1

或

-3

，解方程即可。

拉格朗日插值优化dp

前言：拉格朗日插值作为一种多项式快速求值技巧，在一类dp函数为多项式函数的情况下，往往能够起到很好的降低复杂度的作用，而大多数时候我们所需要做的就是证明dp函数为一个多项式。

拉格朗日插值

用于解决给出不同的

n+1

个点，要求求出一个经过这些点的多项式函数的一类问题，设第

i

个点为

x_i,y_i

。

\sum \limits_{i=1}^{n+1} y_i \prod \limits_{j \neq i} \frac{x-x_j}{x_i-x_j}

simple proof:

考虑将该多项式拆成 $n+1$ 个多项式的和，其中第 $i$ 个多项式在 $x_i$ 处为 $1$ ，而在其它给定的点处为 $0$ 。那么第 $i$ 个多项式 $f_i(x)=\prod \limits_{j \neq i} \frac{x-x_j}{x_i-x_j}$ ，那么显然 $f(x)=\sum \limits_{i=1}^{n+1} y_i\times f_i(x)$ ，于是可以得出上文的式子。

模板： P4781 【模板】拉格朗日插值

我们一般用数学归纳法证明一个函数是多项式，而这需要用到以下三个浅显但重要的结论

一个 $n$ 次的多项式的前缀和是一个 $n+1$ 次多项式。
一个 $n$ 次的多项式的差分是一个 $n-1$ 次多项式。
一个 $n$ 次的多项式与一个 $m$ 次多项式相乘可以得到一个 $n+m$ 次多项式。

当然就如同有人有能肉眼看出函数凸性的异能，如果你有能肉眼看出函数是个多项式的异能，也可以直接不用证明。

感应出函数的多项式之后其实可以不用证次数，直接放尽可能多的点进去插就好了。

例题一

CF995F Cowmpany Cowmpensation

给出一棵树，要求给每个点赋一个不超过 $D$ 的权值，使得每个结点的权值不能超过它父亲的权值（如果它有的话） $n\le 3000,D\le 10^9$ 。

考虑

f_{i,d}

表示点

i

的权值为

d

，以

i

为根的子树的方案数，容易列出dp柿子。

f_{u,d} = \prod \limits_{v\in son_u} \sum \limits_{k=1}^d f_{v,k}

我们现在来证明

f_{i,d}

是关于

d

的

siz_i-1

次多项式。

显然对于叶子节点

f_{i,d}=1

符合条件。

观察柿子，最右边的部分是

f_{v,d}

的一个前缀和，因此是一个

siz_v-1+1=siz_v

次函数，之后将所有

siz_v

次函数乘在一起，得到的

f_{u,d}

就是一个

siz_u-1

次函数。

最后的答案

ans=\sum \limits_{i=0}^D f_{1,i}

就是一个

n

次函数，因此我们对于

d\in[0,n]

求出对应的dp值，之后再用这

n+1

个点拉格朗日插值求出函数在

D

处的值即可。

CPP

#include<bits/stdc++.h>
#define N 3010
#define mod 1000000007
using namespace std;
int read() {
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
	return f*res;
}
int n,d,a[N],f[N][N];
int cnt,head[N],to[N],nxt[N];
void insert(int u,int v) {
	cnt++;
	to[cnt]=v;
	nxt[cnt]=head[u];
	head[u]=cnt;
}
void dfs(int now) {
	for(int i=1; i<=n; i++) f[now][i]=1; 
	for(int i=head[now]; i; i=nxt[i])  {
		dfs(to[i]);
		for(int j=1; j<=n; j++) f[now][j]=1ll*f[now][j]*f[to[i]][j]%mod;
	}
	for(int i=1; i<=n; i++) f[now][i]=(f[now][i]+f[now][i-1])%mod;
}
int qpow(int a1,int a2) {
	int res=1;
	while(a2) {
		if(a2&1) res=1ll*res*a1%mod;
		a1=1ll*a1*a1%mod;
		a2>>=1;
	} return res;
}
int main() {
	n=read(),d=read();
	for(int i=2; i<=n; i++) {
		int fa=read();
		insert(fa,i); 
	} dfs(1);
//	printf("%d\n",f[1][2]);
	int ans=0;
	for(int i=0; i<=n; i++) {
		int s1=f[1][i],s2=1;
		for(int j=0; j<=n; j++) if(i!=j) s1=1ll*s1*(d-j+mod)%mod,s2=1ll*s2*(i-j+mod)%mod;
		ans=(ans+1ll*s1%mod*qpow(s2,mod-2)%mod)%mod;
	}
	printf("%d\n",ans); 
}

第一道例题十分简单，帮助我们快速体验了证明dp函数是多项式函数的步骤。

同样简单的推导多项式性质的练习题：

练习1： P4463 [集训队互测 2012] calc

显然如果题目的dp式子中有前缀和，差分，累乘，且只在邻近层中转移。那么有较大概率是一道拉插优化题。事实上，这题本身也是拉插优化的一个常见类型：带有一些偏序限制的计数问题。

下面我们将讲述两道与例题一类型相似的题，不过难度有较大的提升。

例题二

P3643 [APIO2016] 划艇

为序列上的每个位置 $i$ 赋一个为 $0$ 或在 $[a_i,b_i]$ 之间的权值，使得每个权值不为 $0$ 的点的权值都大于其前面所有点的权值。 $n\le 500,1\le a_i \le b_i \le 10^9$

虽然说用组合数做又短又快，但是拉插作为一种无脑的做法考场上应该更容易想到（？）。

首先普及一个小技巧，当拉格朗日插值所用到的点值是连续的时候，我们可以做到

O(n)

插值。

假设

n+1

个点的横坐标分别是

0,1,2,...,n

，拉格朗日插值的式子变成这样：

\sum \limits_{i=0}^{n} \prod \limits_{j \neq i} y_i \frac{x-j}{i-j}

假设我们想要求得点值横坐标为

k

，那么我们首先求出

pre_i=\prod \limits_{j=0}^i (k-j),suf_i=\prod \limits_{j=i}^n (k-j)

，再预处理出阶乘

fac_i

，原式变为：

\sum \limits_{i=1}^{n+1} (-1)^{n-i} y_i \frac{pre_{i-1}suf_{i+1}}{fac_i fac_{n-i}}

预处理与最后的计算都是

O(n)

的。

线性插值&证多项式性质简单练习:

练习2： The Sum of the k-th Powers

回到正题，显然如果没有下头的区间限制，我们容易写出dp方程：设

f_{i,j}

表示目前dp到了

i

，当前最大值等于

j

的方案数。显然

f_{i,j}=F_{i-1,j}+\sum \limits_{k=0}^{j-1} f_{i-1,k}

显然我们有

f_{1,j}=1

这是一个零次多项式，而转移的方式是做前缀和，因此

f_{i,j}

的次数是

f_{i-1,j}

的次数

+1

，即

f_{i,j}

是个关于

j

的

i-1

次多项式。

预处理前缀和我们就能在

O(n^2)

时间内解决这道题没有区间限制的版本。

现在我们考虑将区间改成左闭右开之后离散化，这样数轴就被我们划分成了

O(n)

个段，而对于同一段内的数，一个点要么都能选，要么都不能选。那么在每一段中

f_{i,j}

都是一个多项式，于是我们分段插值。

我们改设

f_{i,j,k}

表示dp到了

i

，最大值等于第

j

段的第

k

个数。设

g_i

为第

i

段的

f

之和，

s_{i,j}

表示第

i

段的前

j

个

f

之和，

ss_i

表示前

i

段之和。为了方便转移，我们插值的时候插的是

f

的前缀和

s

。

时间复杂度

O(n^3)

CPP

#include<bits/stdc++.h>
#define N 2010 
#define mod 1000000007
using namespace std;
int read() {
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=(res<<3)+(res<<1)+ch-'0',ch=getchar();
	return f*res;
}
int qpow(int a1,int a2) {
	int res=1;
	while(a2) {
		if(a2&1) res=1ll*res*a1%mod;
		a1=1ll*a1*a1%mod,a2>>=1;
	}return res;
}
int n,l[N],r[N],f[N][N],mx,t[N],tn,ss[N],s[N][N],g[N],pre[N],suf[N],fac[N],inv[N];
int md(int a1) {return a1>=mod?a1-mod:a1;}
void add(int& a1,int a2) {a1=md(a1+a2);}
int Lag(int n,int k,int *y) {
	if(k<=n) return y[k];
	pre[0]=k,suf[n]=k-n;
	int res=0;
	for(int i=1; i<=n; i++) pre[i]=1ll*pre[i-1]*(k-i)%mod;
	for(int i=n-1; i; i--) suf[i]=1ll*suf[i+1]*(k-i)%mod;
	for(int i=0; i<=n; i++) 
		add(res,1ll*y[i]*inv[i]%mod*inv[n-i]%mod*(i>0?pre[i-1]:1)%mod*(i<n?suf[i+1]:1)%mod*((n-i)%2?mod-1:1)%mod);
	return res;
}
int main() {
	n=read(),fac[0]=inv[0]=1;
	for(int i=1; i<=n; i++) fac[i]=1ll*fac[i-1]*i%mod;
	inv[n]=qpow(fac[n],mod-2);
	for(int i=n-1; i; i--) inv[i]=1ll*inv[i+1]*(i+1)%mod;
	for(int i=1; i<=n; i++) 
		l[i]=read(),r[i]=read()+1,mx=max(mx,r[i]-1),
		t[++tn]=l[i],t[++tn]=r[i];
	sort(t+1,t+tn+1);
	tn=unique(t+1,t+tn+1)-t-1;
	for(int i=1; i<=n; i++)
		l[i]=lower_bound(t+1,t+tn+1,l[i])-t,
		r[i]=lower_bound(t+1,t+tn+1,r[i])-t;
	for(int i=0; i<tn; i++) ss[i]=1;
	for(int i=1; i<=n; i++) {
		for(int j=l[i]; j<r[i]; j++) {
			for(int k=0; k<=n; k++) add(f[j][k],md(ss[j-1]+(k>0?s[j][k-1]:0)));
			s[j][0]=f[j][0];
			for(int k=1; k<=n; k++) s[j][k]=md(s[j][k-1]+f[j][k]);
			g[j]=Lag(n,t[j+1]-t[j]-1,s[j]);
		} 
		for(int i=1; i<tn; i++) ss[i]=md(ss[i-1]+g[i]);
	}
	printf("%d",ss[tn-1]-1);
}

例题三

P8290 [省选联考 2022] 填树

给出一棵树，求有多少方案在树上选出一条链，给链上每个点赋一个 $[l_i,r_i]$ 之间的权值，使得其最大值和最小值之差 $\le K$ ，此外再输出所有合法方案的权值和（一种方案的权值定义为选出的链的权值和）。

同样的，首先考虑没有区间的限制，我们枚举最小值

L

，只要满足所有值都在

[L,L+K]

之内就好了。

但是枚举最小值很麻烦，因此我们考虑差分。对于

[L,R]

求出每个点权值在

[L,R]

内的方案（实际是

[L,R] \cap [l_i,r_i]

），之后减去每个点权值在

[L+1,R]

之内的方案，就是最小值为

L

的方案数了。

那么我们可以路径的LCA处统计路径，设四个数组

mul_i,pmul_i,tot_i,ptot_i

分别表示以

i

为LCA的路径条数，子树内以

i

为一端的路径条数，以

i

为LCA的路径的权值和，子树内以

i

为一端的路径权值和，就可以简单dp了，复杂度为

O(nV)

。

同样的，我们考虑将值域分成许多段，使得每一段内每个点的状态是固定的（都能选/都不能选）或是匀速变化的（+1/-1）。跟上一题不同的是，上一题中我们移动的是一个点，而这一次我们移动的是一个区间

[L,L+K]

。因此我们将

l_i,l_i-K,r_i,r_i-K

作为段的分界点，之后同样对每一段的前缀和插值即可。

分段插值时如果搞不清楚分多少段，那么在复杂度允许的范围下能分多少就分多少，保证每个段为多项式即可。

复杂度

O(n^3)

CPP

#include<bits/stdc++.h>
#define N 2010
#define mod 1000000007
#define int long long
int n,m=0,K,l[N],r[N];
using namespace std;
int read() {
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
	return f*res;
}
int cnt,head[N],to[N<<1],nxt[N<<1],L,R,a[N],b[N],c[N];
void insert(int u,int v) {
	cnt++;
	to[cnt]=v;
	nxt[cnt]=head[u];
	head[u]=cnt;
}
void add(int& a1,int a2) {a1=(a1+a2>=mod)?a1+a2-mod:a1+a2;}
int mul[N],pmul[N],tot[N],ptot[N],cnt1,cnt2;
int S(int x) {return 1ll*x*(x+1)>>1%mod;}
void dfs(int now,int fa) {
	int ll=max(L,l[now]),rr=min(R,r[now]);
	int len=ll>rr?0:rr-ll+1,sum=ll>rr?0:(S(rr)-S(ll-1)+mod)%mod;
	pmul[now]=mul[now]=len,ptot[now]=tot[now]=sum;
	for(int i=head[now]; i; i=nxt[i]) if(to[i]!=fa) {
		dfs(to[i],now);
		add(mul[now],1ll*pmul[now]*pmul[to[i]]%mod);
		add(tot[now],(1ll*ptot[to[i]]*pmul[now]%mod+1ll*pmul[to[i]]*ptot[now])%mod);
		add(pmul[now],1ll*pmul[to[i]]*len%mod);
		add(ptot[now],(1ll*ptot[to[i]]*len%mod+1ll*pmul[to[i]]*sum%mod)%mod);
	}
}
int pos[N];
void work(int f) {
	dfs(1,0);
	for(int i=1; i<=n; i++) cnt1+=mul[i]*f,cnt2+=tot[i]*f;
	cnt1=(cnt1+mod)%mod,cnt2=(cnt2+mod)%mod;
}
int qpow(int a1,int a2) {
	int res=1;
	while(a2) {
		if(a2&1) res=1ll*res*a1%mod;
		a1=1ll*a1*a1%mod;
		a2>>=1;
	} return res;
}
int Lag(int len,int x,int *a1,int *a2) {
	int res=0;
	for(int i=0; i<len; i++) {
		int s1=a2[i]%mod,s2=1;
		for(int j=0; j<len; j++) if(i!=j) s1=1ll*s1*(x-a1[j])%mod,s2=1ll*s2*(a1[i]-a1[j])%mod;
		add(res,1ll*s1*qpow(s2,mod-2)%mod);
	} return res;
}
signed main()  {
	n=read(),K=read();
	for(int i=1; i<=n; i++) {
		l[i]=read(),r[i]=read();
		pos[++m]=l[i],pos[++m]=max(l[i]-K,0ll),pos[0]=max(pos[0],r[i]+1);
		pos[++m]=r[i],pos[++m]=max(r[i]-K,0ll);
	}
	sort(pos,pos+m+1),m=unique(pos,pos+m+1)-pos-1;
	for(int i=1; i<n; i++) {
		int u=read(),v=read();
		insert(u,v);
		insert(v,u);
	}
	for(int i=0,j; i<m; i++) {
		L=pos[i],R=pos[i]+K;
		for(j=0; j<n+2; j++,R++) {
			if(pos[i]+j==pos[i+1]) break;
			work(1),++L,work(-1);
			a[j]=pos[i]+j,b[j]=cnt1,c[j]=cnt2;
		}
		if(pos[i]+j<pos[i+1]) cnt1=Lag(j,pos[i+1]-1,a,b),cnt2=Lag(j,pos[i+1]-1,a,c);
	}
	printf("%d\n%d",cnt1,cnt2);
}

稍有不同的分段插值：

练习3： P7116 [NOIP2020] 微信步数

进阶题

练习4： P5469 [NOI2019] 机器人

这题的主体其实已经是dp不是拉插了，可以采用拉插之外的方法维护多项式，拉插的话依旧是经典的分段插值。

Polya定理与Burnside引理

一、群的定义

若存在一个集合

S

与一个二元运算

·

满足以下性质

封闭性 (Closure)： $\forall a,b \in S,a·b \in S$

结合律 (Associativity)： $\forall a,b,c \in S, (a·b)·c=a·(b·c )$

单位元/幺元 (Identity element)： $\exists e \in S ,\forall a \in S ,e·a=a·e=a$

逆元 (Inverse element)： $\forall a \in S, \exists b \in S,a·b=b·a=e$ 此处称 $b$ 为 $a$ 的逆元，记作 $b=a^{-1}$

满足这些性质的集合与二元运算的二元组

(S,·)

被称作一个群。

生活中有许多常见的群，如整数加法群

(\mathbb{Z},+)

与正实数乘法群

(\mathbb{+R},\times)

,可以尝试自己证明这些群的性质。

群

G

的大小即为集合

S

的大小，也可以用

x \in G

表示

x

是群中的元素。和集合有子集一样，群也有子群，不过这个之后再提。

下面开始的定理都只能作用于有限群。事实上，在同构意义下，所有有限群都同构于一个置换群（可以简单的理解成有限群就是置换群）。

二、置换

定义

有限集合到自身的双射称为置换，例如对于一个集合

S={a_1,a_2,a_3,...,a_n}

，那么它的一个置换可以表示为

\sigma=\begin{pmatrix}a_{p_1},a_{p_2},\dots,a_{p_{n-1}},a_{p_n}\\ a_{q_1},a_{q_2},\dots,a_{q_{n-1}},a_{q_n}\end{pmatrix}

该置换意为将

a_{p_i}

置换为

a_{q_i}

，其中

p_1,p_2,\dots,p_n

与

q_1,q_2,\dots,q_n

均为

1,2,\dots,n

的排列。

由于在交换置换中第一行的

a_{p_i},a_{p_j}

的同时交换第二行的

a_{q_i},a_{q_j}

所得到的置换是本质相同的，因此我们默认第一行为

a_1,a_2,\dots,a_n

，此时置换可以直接写作

\sigma=(a_{p_1},a_{p_2},\dots,a_{p_n})

大小为

n

的集合

S

的本质不同的置换有

n!

种。

置换乘法

置换

f=\begin{pmatrix}a_1,a_2,\dots,a_{n-1},a_n\\ a_{p_1},a_{p_2},\dots,a_{p_{n-1}},a_{p_n}\end{pmatrix}

与置换

g=\begin{pmatrix}a_{p_1},a_{p_2},\dots,a_{p_{n-1}},a_{p_n}\\ a_{q_1},a_{q_2},\dots,a_{q_{n-1}},a_{q_n}\end{pmatrix}

的乘积

f \circ g = \begin{pmatrix}a_1,a_2,\dots,a_{n-1},a_n\\ a_{q_1},a_{q_2},\dots,a_{q_{n-1}},a_{q_n}\end{pmatrix}

循环置换

循环置换是一种特殊的置换，可表示为

(a_1,a_2,\dots,a_{n-1},a_n)=\begin{pmatrix}a_1,a_2,\dots,a_{n-1},a_n\\ a_2,a_3,\dots,a_n,a_1\end{pmatrix}

即将

a_1,a_2,\dots,a_n

向前循环移位一位。

若两个循环置换没有相同元素，则称其 不相交 。

任意一个置换都可以分解为若干不相交的循环置换的乘积，例如

\begin{pmatrix}a_1,a_2,a_3,a_4,a_5\\ a_3,a_1,a_2,a_5,a_4\end{pmatrix}=(a_1,a_3,a_2)\circ(a_4,a_5)

证明可以看做是从

a_{q_i}

向

a_{p_i}

连一条边，那么置换构成的图必定是由若干个环组成的，每个环都是一个循环置换。

置换群

大小为

n

的集合

S

上的所有

n!

个置换与置换乘法

\circ

构成的群称为 $n$ 级对称群 ，记作

S_n

，显而易见其满足群的性质。

对称群的子群称作 置换群 。

所有的循环置换也可以构成一类特殊的置换群，我们称其为 循环群 。

三、轨道-稳定子定理

群作用

设定一个群

G=(S,·)

与一个集合

T

，定义运算

\phi(g,a),g\in S,a\in T

表示群中的元素

g

作用集合中的元素

a

，也可以写作

g(a)

（此处可以将群中的元素看做一种 运算/操作）。这里可能比较难懂，具体可以看后面的例题。

如果满足

\forall a\in T,\phi(e,a)=a

\forall a\in T,f\in S,g\in S,\phi(f,\phi(g,a))=\phi(f·g,a)

则称群

G

作用于集合

T

。

特别一提，群作用是可逆的（群中元素存在逆元），即对于

g\in S,x \neq y \Leftrightarrow g(x) \neq g(y)

下面开始的定理中群作用的集合都为有限集。

轨道

设群

G

作用于集合

U

，则对于元素

x\in U

，

x

的轨道

G(x)

可以表示为集合

\{g(x)|g\in S\}

。即群

G

中的元素作用于

x

能达到的集合。

稳定子

对于元素

x\in U

，

x

的稳定子

G^x

表示为

\{g|g\in S,g(x)=x\}

,即群中满足

g(x)=x

的

g

构成的集合。

轨道-稳定子定理

|G^x|\times |G(x)|=|G|

即元素

x

的稳定子个数乘以轨道个数等于群的大小。

四、Burnside引理

等价类

设群

G

作用于集合

X

，若对于

x,y\in X

，存在

g \in G

使得

g(x)=y

，则称

x,y

属于同一等价类。

对于一类等价类计数问题，我们可以使用Burnside引理

|X/G|=\frac{1}{|G|}\sum_{g\in G} X^g

其中

|X/G|

表示集合

X

在群

G

作用下的等价类的数量，而

X^g

表示

X

在群中元素

g

的作用下的不动点的数量，即集合中满足

g(x)=x

的

x

的数量。

五、Pólya定理

Burnside引理中群

G

作用的集合

X

是任意的，而Pólya定理中集合

X

必须是一个集合

A

到一个集合

B

的所有映射构成的集合。

一般情况下，Pólya定理使用于经典的染色问题，即将

n

个元素染成

m

种颜色，那么群

G

为

n

个元素的所有置换构成的集合，集合

A

为

n

个元素，集合

B

为

m

种颜色，集合

X

为集合

A

到一个集合

B

的所有映射构成的集合，即将

n

个元素染成

m

种颜色的所有方案构成的集合。

Pólya定理为

|X/G|=\frac{1}{G}\sum_{g\in G} |B|^{c(g)}

在染色问题上，设不同构染色方案数为

L

，这个公式即为

L=\frac{1}{G}\sum_{g\in G} m^{c(g)}

解决一般的染色问题直接记下面的公式就好了。

其中

c(g)

表示置换

g

的环数，即设置换

g

为

(a_1,a_2,...,a_n)

,从

i

往

a_i

连一条边，建出来的图中的环的数量，也可以说成是置换

g

能拆分成的不相交的循环置换的数量。

例题Part

P1446 [HNOI2008] Cards

题目中的

输入数据保证任意多次洗牌都可用这 $m$ 种洗牌法中的一种代替，且对每种洗牌法，都存在一种洗牌法使得能回到原状态。

显然这是在告诉我们所有给出的置换构成了一个群。这启发我们想到 Burnside 引理。根据 Burnside 引理，我们只需求出其在每种置换下的不动点数量即可。考虑每一个循环只能染一种颜色，结合题目对每种颜色数量的限制，我们使用一个背包来统计方案数，设

f_{i,j}

表示第一种颜色染了

i

个点，第二种颜色染了

j

个点的方案数（这里其实可以做一个优化，因为我们可以选择一种颜色不统计，所以我们可以选择最多的颜色数不去统计，这样状态数最多为

\frac{n^2}{9}

，但本题数据范围较小所以随便 dp 都能过）。

CPP

#include<bits/stdc++.h>
#define N 65
#define pb push_back
using namespace std;
int n,n1,n2,n3,m,mod,a[N],vis[N],f[25][25],ans;
void add(int& a1,int a2) {a1=a1+a2>=mod?a1+a2-mod:a1+a2;}
int qpow(int a1,int a2) {
	int res=1;
	while(a2) {
		if(a2&1) res=1ll*res*a1%mod;
		a1=1ll*a1*a1%mod;
		a2>>=1;
	} return res;
}
int main() {
	cin.tie(0)->sync_with_stdio(0);
	cin>>n1>>n2>>n3>>m>>mod;
	n=n1+n2+n3;
	for(int i=0; i<=m; i++) {
		vector<int> v;
		if(i) for(int j=1; j<=n; j++) cin>>a[j],vis[j]=0;
		else for(int j=1; j<=n; j++) a[j]=j;
		for(int j=1; j<=n; j++) if(!vis[j]) {
			int tot=1,tmp=a[j];vis[j]=1;
			while(tmp!=j) tot++,vis[tmp]=1,tmp=a[tmp];
			v.pb(tot);
		}
		for(int i=0; i<=n1; i++)
			for(int j=0; j<=n2; j++) f[i][j]=0;
		f[0][0]=1;
		for(int x:v) 
			for(int p=n1; ~p; p--)
				for(int q=n2; ~q; q--) {
					if(p>=x) add(f[p][q],f[p-x][q]);
					if(q>=x) add(f[p][q],f[p][q-x]);
				}
		add(ans,f[n1][n2]);
	} printf("%d\n",1ll*ans*qpow(m+1,mod-2)%mod);
}

wqs二分相关

当贡献全为整数时，凸包相邻两点的斜率为整数，因此只需要二分整数斜率即可。有多点共线需要通过斜率算出真正答案。

注意只有二分到小数且无3点共线时可以求出具体方案。

文章操作

放宽限制

差分贡献

组合意义

分数计算

dsu on tree

决策单调性

prufer序列相关

一类kth-element问题

Slope trick

CF713C Sonya and Problem Wihtout a Legend

一类集合计数问题

拉格朗日插值优化dp

例题一

例题二

例题三

Polya定理与Burnside引理

一、群的定义

二、置换

三、轨道-稳定子定理

四、Burnside引理

五、Pólya定理

例题Part

P1446 [HNOI2008] Cards

wqs二分相关

相关推荐

评论

Trick合集