专栏文章
2025.11.3
个人记录参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @mine1zu3
- 此快照首次捕获于
- 2025/12/02 00:53 3 个月前
- 此快照最后确认于
- 2025/12/02 00:53 3 个月前
T1:折半秒了。
CPP#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5;
int n, m, k, a[25][25], ans;
vector <int> v[25][25];
void dfs1 (int i, int j, int sum) {
if (i > n || j > m) return;
if (i + j == m + 1) {
v[i][j].push_back(sum);
return;
}
dfs1 (i + 1, j, sum ^ a[i][j]);
dfs1 (i, j + 1, sum ^ a[i][j]);
return;
}
void dfs2 (int i, int j, int sum) {
if (i < 1 || j < 1) return;
if (i + j == m + 1) {
ans += upper_bound(v[i][j].begin(), v[i][j].end(), sum ^ k) - lower_bound(v[i][j].begin(), v[i][j].end(), sum ^ k);
return;
}
dfs2 (i - 1, j, sum ^ a[i - 1][j]);
dfs2 (i, j - 1, sum ^ a[i][j - 1]);
return;
}
signed main() {
scanf("%lld%lld%lld", &n, &m, &k);
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= m; ++ j )
scanf("%lld", &a[i][j]);
dfs1 (1, 1, 0);
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= m; ++ j )
sort(v[i][j].begin(), v[i][j].end());
dfs2 (n, m, a[n][m]);
printf("%lld\n", ans);
return 0;
}
T2:读懂题目比较费劲,但只要反应过来这玩意要结合图论,就显然相邻点连边 tarjan,然后发现每个序列的位置所属于的强连通分量一定是若干块,前缀和即可。
CPP#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5;
int T, n, k, Q, dfn[N], low[N], idx, c[N], cnt;
vector <int> a[N], q[N], h[N], sum[N];
vector <int> g[N];
stack <int> s;
bool is[N];
void tarjan (int u) {
dfn[u] = low[u] = ++ idx;
s.push(u);
is[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (is[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++ cnt;
int t = 0;
do {
t = s.top();
s.pop();
is[t] = false;
c[t] = cnt;
} while (t != u);
}
return;
}
signed main() {
scanf("%lld", &T);
while (T -- ) {
scanf("%lld%lld%lld", &n, &k, &Q);
for (int i = 1; i <= k; ++ i ) {
a[i].clear();
a[i].push_back(0);
for (int j = 1; j <= n; ++ j ) {
int x;
scanf("%lld", &x);
a[i].push_back(x);
}
}
idx = 0, cnt = 0;
for (int i = 1; i <= n; ++ i ) dfn[i] = low[i] = 0, is[i] = false, g[i].clear();
for (int i = 1; i <= k; ++ i )
for (int j = 1; j < n; ++ j )
g[a[i][j]].push_back(a[i][j + 1]);
for (int i = 1; i <= n; ++ i )
if (!dfn[i])
tarjan(i);
for (int i = 1; i <= k; ++ i ) {
sum[i].clear();
sum[i].push_back(0);
q[i].clear();
q[i].push_back(0);
h[i].clear();
h[i].push_back(0);
for (int j = 1; j <= n; ++ j ) {
int l = j;
while (j <= n && c[a[i][j]] == c[a[i][l]]) ++ j;
-- j;
for (int k = l; k <= j; ++ k ) q[i].push_back(l);
for (int k = l; k <= j; ++ k ) h[i].push_back(j);
int len = j - l + 1;
for (int k = l; k <= j; ++ k ) sum[i].push_back(len * (len - 1) / 2 + sum[i][l - 1]);
}
}
int lst = 0;
while (Q -- ) {
int id, l, r;
scanf("%lld%lld%lld", &id, &l, &r);
id = (id + lst) % k + 1;
l = (l + lst) % n + 1;
r = (r + lst) % n + 1;//cout << "K" << id << ' ' << l << ' ' << r << endl;
int L = h[id][l], R = q[id][r];
if (L >= R) {
printf("%lld\n", lst = (r - l + 1) * (r - l) / 2);
continue;
}
int len1 = L - l + 1, len2 = r - R + 1;
int ans = sum[id][R - 1] - sum[id][L] + len1 * (len1 - 1) / 2 + len2 * (len2 - 1) / 2;
printf("%lld\n", lst = ans);
}
}
return 0;
}
T3:如图:
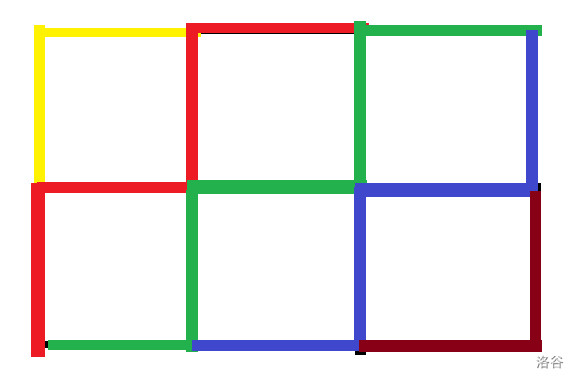
不同颜色不会互相影响,因此预处理一串棱的情况,再撑在一起,递增的部分预处理答案,中间的快速幂即可。
CPP#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6 + 5, mod = 998244353;
int ksm (int a, int n) {
int ans = 1;
while (n) {
if (n & 1) ans = ans * a % mod;
a = a * a % mod;
n >>= 1;
}
return ans;
}
int T, h, w, f[N][2], sum[N];
signed main() {
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= 2e6; ++ i ) {
f[i][0] = (f[i - 1][0] + f[i - 1][1]) % mod;
f[i][1] = f[i - 1][0];
}
sum[0] = 1;
for (int i = 1; i <= 1e6; ++ i ) sum[i] = sum[i - 1] * (f[i * 2 - 1][0] + f[i * 2 - 1][1]) % mod;
scanf("%lld", &T);
while (T -- ) {
scanf("%lld%lld", &h, &w);
int ans = sum[min(h, w)] * sum[min(h, w)] % mod;
ans = ans * ksm ((f[min(h, w) * 2][0] + f[min(h, w) * 2][1]), abs(h - w)) % mod;
printf("%lld\n", ans);
}
return 0;
}
T4:顺着贪心,先确定左端点,右边的不合法了给左端点结尾即可,反正挺难想,但很好写。
CPP#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6 + 5, mod = 998244353;
int n, x[N], y[N];
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; ++ i ) scanf("%lld", x + i);
for (int i = 1; i <= n; ++ i ) scanf("%lld", y + i);
deque <pair <int, int> > q;
int ans = 1e18;
x[0] = -1e18;
for (int i = 1; i <= n; ++ i ) {
if (y[i] == y[i - 1]) continue;
if (y[i] > y[i - 1]) {
q.push_back({x[i - 1] + 1, y[i] - y[i - 1]});
continue;
}
int d = y[i - 1] - y[i];
while (q.size() && q.front().second <= d) {
ans = min(ans, x[i] - 1 - q.front().first);
d -= q.front().second;
q.pop_front();
}
if (q.size() && d) {
q[0].second -= d;
ans = min(ans, x[i] - 1 - q[0].first);
}
}
if (ans > 1e15) puts("-1");
else printf("%lld\n", ans);
return 0;
}
T5:容斥,然后利用矩阵树做完了,难点矩阵树,并不会证明。
CPP#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6 + 5, mod = 1e9 + 7;
int n, m[N], d[25][25];
struct edge {
int u, v;
};
vector <edge> e[N];
int solve () {
int ans = 1;
for (int i = 1; i <= n; ++ i ) {
int at = -1;
for (int j = i; j <= n; ++ j )
if (d[i][j]) {
at = j;
break;
}
if (at == -1) return 0;
if (i != at) {
for (int k = 1; k <= n; ++ k ) swap(d[k][i], d[k][at]);
ans = (mod - ans) % mod;
}
for (int j = i + 1; j <= n; ++ j ) {
while (d[j][i]) {
int tmp = d[j][i] / d[i][i];
for (int k = i; k <= n; ++ k ) {
(d[j][k] -= tmp * d[i][k] % mod - mod) %= mod;
d[j][k] = (d[j][k] % mod + mod) % mod;
}
if (!d[j][i]) break;
swap(d[i], d[j]);
ans = (mod - ans) % mod;
}
}
(ans *= d[i][i]) %= mod;
}
return ans;
}
signed main() {
scanf("%lld", &n);
-- n;
for (int i = 1; i <= n; ++ i ) {
scanf("%lld", m + i);
for (int j = 1, u, v; j <= m[i]; ++ j ) {
scanf("%lld%lld", &u, &v);
e[i].push_back({u, v});
}
}
int ans = 0;
for (int t = 1; t < (1 << n); ++ t ) {
memset(d, 0, sizeof(d));
int cnt = 0;
for (int j = 1; j <= n; ++ j ) {
if (t >> (j - 1) & 1) {
++ cnt;
for (auto k : e[j]) {
int u = k.u, v = k.v;
++ d[u][v], ++ d[v][u];
-- d[u][u], -- d[v][v];
}
}
}
if (cnt & 1) (ans -= solve() - mod) %= mod;
else (ans += solve()) %= mod;
}
printf("%lld\n", (ans % mod + mod) % mod);
return 0;
}
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...