专栏文章

树上背包时间复杂度证明

xxht叉叉
算法·理论参与者 30已保存评论 30

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
30 条
当前快照
1 份
快照标识符
@minuxb9c
此快照首次捕获于
2025/12/02 08:45
3 个月前
此快照最后确认于
2025/12/02 08:45
3 个月前
查看原文
P2014 [CTSC1997] 选课
本文证明树上背包的时间复杂度是 O(nm)\mathcal O(nm) 的。换言之，上题可以加强至：n≤3×105n \le 3 \times 10^5，m≤300m \le 300。
首先给出代码实现：
CPP
#include <bits/stdc++.h>
using namespace std;

#define dbg(...) cerr << "[" << #__VA_ARGS__ << "] = ", debug_out(__VA_ARGS__)
template <typename T> void debug_out(T t) { cerr << t << endl; }
template <typename T, typename... Ts> void debug_out(T t, Ts... ts) {
	cerr << t << ", ";
	debug_out(ts...);
}

template <class F> struct y_combinator {
	F f;
	template <class... Args> decltype(auto) operator()(Args &&...args) {
		return f(*this, std::forward<Args>(args)...);
	}
};
template <class F> auto make_y_combinator(F f) { return y_combinator<F>{f}; }

int main() {
	cin.tie(0)->sync_with_stdio(0);
	int n, m;
	cin >> n >> m;
	vector<int> a(n + 1);
	vector<vector<int>> e(n + 1);
	for (int i = 1, f; i <= n; i++) {
		cin >> f >> a[i];
		e[f].emplace_back(i);
	}
	++m;
	vector<vector<int>> dp(n + 1, vector<int>(m + 1));
	vector<int> sz(n + 1);
	auto dfs = make_y_combinator([&](auto self, int u) -> void {
		dp[u][1] = a[u];
		sz[u] = 1;
		for (int v : e[u]) {
			self(v);
			for (int i = min(sz[u], m); i >= 1; i--) {
				for (int j = min(sz[v], m - i); j >= 1; j--) {
					dp[u][i + j] = max(dp[u][i + j], dp[u][i] + dp[v][j]);
				}
			}
			sz[u] += sz[v];
		}
	});
	dfs(0);
	cout << dp[0][m] << endl;
	return 0;
}
让我们重点关注：
CPP
for (int i = min(sz[u], m); i >= 1; i--) {
	for (int j = min(sz[v], m - i); j >= 1; j--) {
		dp[u][i + j] = max(dp[u][i + j], dp[u][i] + dp[v][j]);
	}
}
这也就是说，对于每条边 u→vu \to v，该部分转移的时间复杂度为
O(min⁡(m,prev)×min⁡(m,sizv))\mathcal O(\min(m, pre_v) \times \min(m, siz_v))
其中：
  • prevpre_v 表示 vv 左边的子树大小之和，即 uu 的子节点中在 vv 之前被访问到的子节点的子树大小之和。
  • sizvsiz_v 表示 vv 的子树大小。
那么总时间复杂度即为
O(∑u→vmin⁡(m,prev)×min⁡(m,sizv))\mathcal O\left(\sum_{u \to v} \min(m, pre_v) \times \min(m, siz_v)\right)
接下来存在两个 自然的观察：
  1. 考虑 min⁡(m,prev)×min⁡(m,sizv)≤m2\min(m, pre_v) \times \min(m, siz_v) \le m^2，由于边数 O(n)O(n)，因此总时间复杂度不超过 O(nm2)\mathcal O(nm^2)。
  2. 考虑 min⁡(m,prev)×min⁡(m,sizv)≤prev⋅sizv\min(m, pre_v) \times \min(m, siz_v) \le pre_v \cdot siz_v，这可以理解成在 u→vu \to v 处对所有满足如下条件的 (x,y)(x, y) 进行计数：
    • xx 在 vv 左边的子树 中
    • yy 在 vv 的子树 中
    注意到任意 (x,y)(x,y) 仅会在它们的 lca\text{lca} 处被计数一次，于是有 ∑u→vprev⋅sizv≤n2\sum_{u\to v} pre_v \cdot siz_v \le n^2，因此总时间复杂度不超过 O(n2)\mathcal O(n^2)。
然未尽其析。
下证时间复杂度为 O(nm)\mathcal O(nm)。
我们将子树大小 ≤m\le m 的点称之为蓝点，子树大小 >m> m 的点称之为红点。
同时把边分为三类：
  • 蓝边：连接两个蓝点的边
  • 黄边：连接红点和蓝点的边
  • 红边：连接两个红点的边
例如 n=20n = 20，m=3m = 3 时，考虑下图：
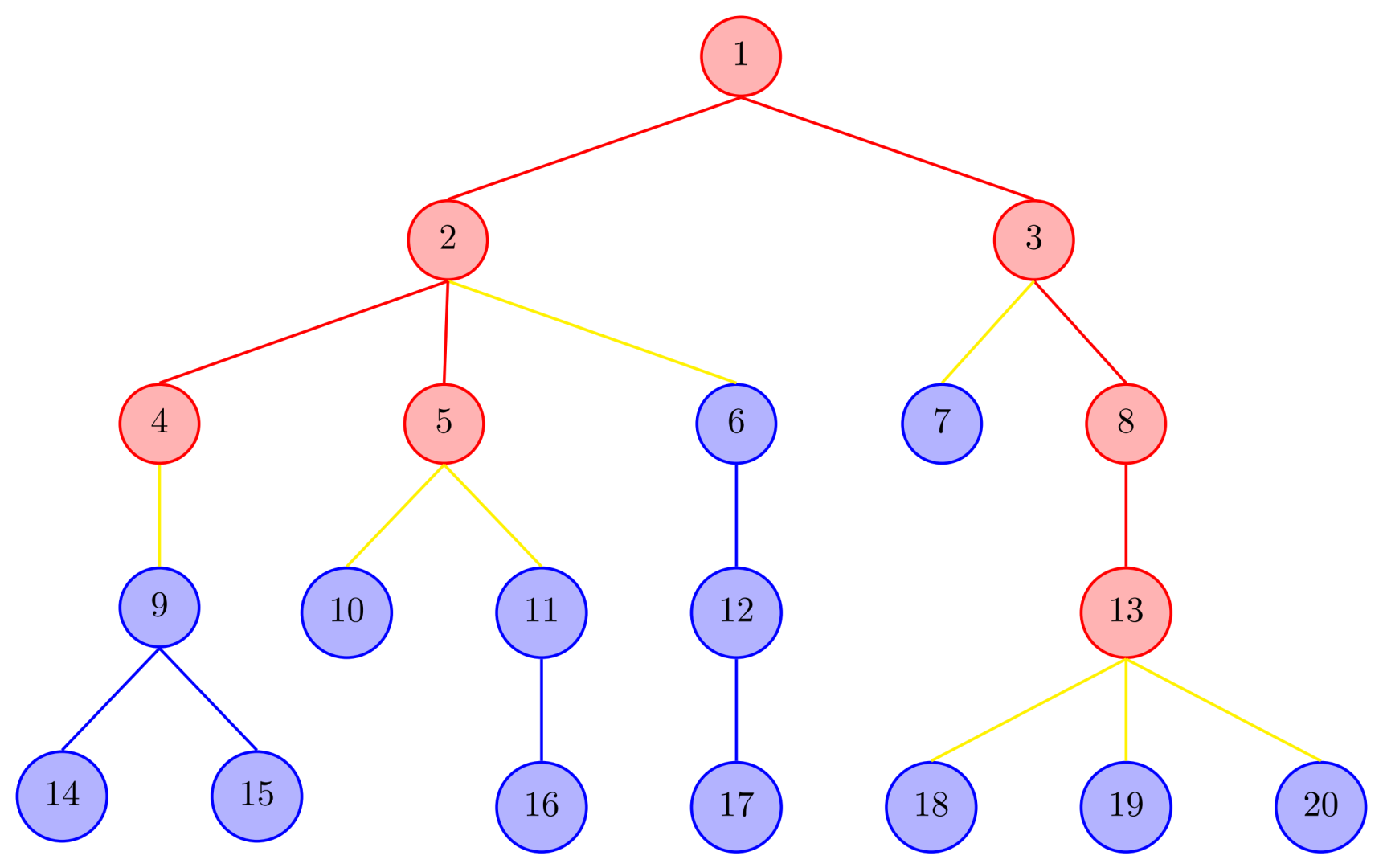
接下来我们分四类讨论：
考虑所有蓝边，我们可以得到若干 极大蓝子树（图中有蓝点 6, 7, 9, 10, 11, 18, 19, 20 的子树）。根据上述 自然的观察 2，大小为 ss 的子树内部对时间复杂度的贡献不超过 O(s2)\mathcal O(s^2)。假设这些 极大蓝子树 的大小为 sis_i，则：
  • si≤ms_i \le m。
  • 由于 极大蓝子树 是互斥的，有 ∑si≤n\sum s_i \le n。
这可以推出
∑si2≤∑si⋅m≤nm\sum s_i^2 \le \sum s_i \cdot m \le nm
于是所有蓝边对时间复杂度的贡献不超过 O(nm)\mathcal O(nm)。
考虑所有黄边 u→vu \to v，此时所有 vv 的子树即为 极大蓝子树，它们是互斥的，有 ∑sizv≤n\sum siz_v \le n，因此
∑min⁡(m,prev)×min⁡(m,sizv)≤∑m⋅sizv≤mn\sum \min(m, pre_v) \times \min(m, siz_v) \le \sum m \cdot siz_v \le mn
于是所有黄边对时间复杂度的贡献不超过 O(nm)\mathcal O(nm)。
注意到仅红点和红边也构成一棵树，我们称之为红树。
考虑 红树的叶子节点，其个数为 O(nm)\mathcal O\left(\dfrac nm\right)，这是因为在原树中这些点的子树大小均 >m> m，且这些子树互斥。
仅考虑满足如下条件的红边 u→vu \to v（让我们称之为 深红边）：
  • uu 有至少两个红子节点（让我们称之为 深红点）。
（图中有 深红边 1→21\to 2，1→31 \to 3，2→42 \to 4，2→52 \to 5，深红点 1,21,2）
可以将每个 深红点 理解为，对至少两个 红树的叶子节点 进行合并。因此 深红点 的个数 << 红树的叶子节点 的个数，从而 深红边 的数量也为 O(nm)\mathcal O\left(\dfrac nm\right)。
根据上述 自然的观察 1，每条边对时间复杂度的贡献不超过 O(m2)\mathcal O(m^2)，因此所有 深红边 对时间复杂度的贡献不超过 O(nm×m2)=O(nm)\mathcal O\left(\dfrac nm \times m^2\right) = \mathcal O(nm)。
最后考虑 浅红边 u→vu \to v（即不是 深红边 的红边，图中有 3→83 \to 8，8→138 \to 13），此时所有 vv 左边的子树 是互斥的，有 ∑prev≤n\sum pre_v \le n，因此
∑min⁡(m,prev)×min⁡(m,sizv)≤∑prev⋅m≤nm\sum \min(m, pre_v) \times \min(m, siz_v) \le \sum pre_v \cdot m \le nm
于是所有 浅红边 对时间复杂度的贡献不超过 O(nm)\mathcal O(nm)。
综上，树上背包时间复杂度不超过 O(nm)\mathcal O(nm)，这显然没法更低了，因此就是 O(nm)\mathcal O(nm)。
然犹未尽析。
有没有更直观一点的解释呢？
回到式子：
min⁡(m,prev)×min⁡(m,sizv)\min(m, pre_v) \times \min(m, siz_v)
考虑 dfs 序 dfndfn，仿照 自然的观察 2，这可以理解成在 u→vu \to v 处对所有满足如下条件的 (x,y)(x, y) 进行计数：
  • xx 在 vv 左边的子树 中，且 dfnx≥dfnv−mdfn_x \ge dfn_v - m
  • yy 在 vv 的子树 中，且 dfny<dfnv+mdfn_y < dfn_v + m
注意到任意 (x,y)(x,y) 仅会在它们的 lca\text{lca} 处被最多计数一次，且只有当 dfny−dfnx<2mdfn_y - dfn_x < 2m 才会被计数。这样的 (x,y)(x,y) 有 O(nm)\mathcal O(nm) 对，因此总时间复杂度为 O(nm)\mathcal O(nm)。

评论

共 30 条评论，欢迎与作者交流。

正在加载评论...