图上进阶算法初探

省流：LCA，树上差分，重链剖分，差分约束，tarjan，2 - SAT，二分图基础，基环树。

放在前面

本文并非“图论进阶算法教程”，仅用于快速记忆图论核心进阶算法的基础原理、实现逻辑与实用性。

图论作为信息学竞赛的核心板块，贯穿路径查询、约束求解、匹配优化等各类问题，从简单的树结构到复杂的有向图，都需要针对性算法突破效率瓶颈。

本文总结的算法均围绕“图的结构特性”展开：树上问题侧重“祖先关系”与“路径拆分”，有向图问题聚焦“强连通性”与“约束转化”，特殊图（二分图、基环树）则针对其独特结构设计优化方案。通过具体例题理解算法适配场景，是掌握图论的关键。

前置知识：图的邻接表存储、二分与倍增思想、BFS / DFS、并查集、线段树基础、最短路，MST。

最近公共祖先、树上前缀和、树上差分

Ⅰ. 最近公共祖先

对于一棵有根树，如果以

x

为根的子树中同时含有

a,b

两点，则称

x

是

a,b

的公共祖先。点对

(a,b)

的公共祖先集合中，定义深度最小的为

(a,b)

的最近公共祖先，记作

\textrm{LCA}(a,b)

。

明显有以下性质：

$\textrm{LCA}(A,B)$ 是 $A \to \textrm{root}$ 和 $B \to \textrm{root}$ 两条路径的最深交点；
$\textrm{LCA}(A,B)$ 是 $A \to B$ 路径上深度最小的节点；
链 $A \to B$ 可以拆分为 $A \to \textrm{LCA}(A,B)$ 和 $B \to \textrm{LCA}(A,B)$ 。

因此，求出树中两点的最近公共祖先就显得尤为重要。

板子：最近公共祖先。

给定一棵有根树，请回答 $m$ 次询问，每次询问输出给定点对 $(a,b)$ 的最近公共祖先。

$n,m \le 5 \times 10^5$ 。

向上标记法

一遍深搜处理出所有节点的父节点以及深度，然后对于每一次询问，先把更深的节点往上跳到与另一个节点一样的深度，然后再一起一步一步往上跳，直到跳到同一个点，这个点就是它们的 LCA。

显然最坏时间复杂度出现在链上，为

\mathcal{O}(n)

。

树上倍增法

如果一次不止跳一步，也许速度会更快。因此，倍增法能更加成功地处理 LCA。

考虑预处理出每个节点的深度和祖先关系。

定义

f_{i,j}

表示从

i

号点往上跳

2^j

步后的节点（如果跳不动就认为是根节点）。在祖先的祖先关系都处理好之后，子节点跳

2^j

步的结果其实就相当于其

2^{j-1}

级组先跳

2^{j-1}

步的结果，直接在递归前

\mathcal{O}(\log n)

处理即可。显然一次预处理的时间复杂度是

\mathcal{O}(n \times \log n)

。

CPP

inline void dfs(int x,int fa){
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(int i=1; i<=20; i++) f[x][i]=f[f[x][i-1]][i-1];
	for(int i=0; i<v[x].size(); i++){
		int y=v[x][i];
		if(y==fa) continue;
		dfs(y,x);
	}
}

接下来在跳动的时候就可以直接跳

2^i

步了。按照倍增思想，做法如下：

要求 $A$ 和 $B$ 的最大公共祖先，首先要找出最深的那个，考虑放在 $A$ 处。
将深度大的往上跳，所以倒序枚举 $i$ ，若深度仍然小于 $B$ 就跳 $2^i$ 步。
一起跳。排除跳多的情况即 $A=B$ ，最后 $A$ 的父亲就是 $\textrm{LCA}(A,B)$ 。

时间复杂度

\mathcal{O}(\log n)

。

CPP

inline int lca(int a,int b){
	if(dep[a]<dep[b]) swap(a,b);
	for(int i=20; i>=0; i--){
		if(dep[f[a][i]]>=dep[b]) a=f[a][i];
	}
	if(a==b) return a;
	for(int i=20; i>=0; i--){
		if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
	}
	return f[a][0];
}

使用预处理 + 每次查询

\log

优化，总时间复杂度就变为了

\mathcal{O}((n+m) \times \log n)

。

代码

CPP

#include<cstdio>
#include<vector>
int s;
char ch;
inline int read() {
	s=0;
	while((ch=getchar())<48);
	do s=(s<<3)+(s<<1)+(ch^48);
	while((ch=getchar())>47);
	return s;
}
inline void write(int x) {
	if(x>9) write(x/10);
	putchar(x%10+48);
}
std::vector<int> v[500005];
int n,m,a,b,dep[500005],f[500005][21],dis,qa,root,itemc;
inline void dfs(int x,int fa){
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(int i=1; i<=20; i++) f[x][i]=f[f[x][i-1]][i-1];
	for(int i=0; i<v[x].size(); i++){
		int y=v[x][i];
		if(y==fa) continue;
		dfs(y,x);
	}
}
inline int lca(int a,int b){
	if(dep[a]<dep[b]){
		itemc=a;
		a=b;
		b=itemc;
	}
	for(int i=20; i>=0; i--){
		if(dep[f[a][i]]>=dep[b]) a=f[a][i];
	}
	if(a==b) return a;
	for(int i=20; i>=0; i--){
		if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
	}
	return f[a][0];
}
int main() {
	n=read();
	m=read();
    root=read();
	for(int i=1; i<n; i++){
		a=read(), b=read();
		v[a].push_back(b);
		v[b].push_back(a); 
	} 
	dfs(root,0);
	while(m--){
		qa=read();
		write(lca(qa,read()));
        putchar('\n');
	} 
	return 0;
}

Ⅱ. 最近公共祖先所具有的性质

结合律

\forall a,b,c \in V,\textrm{LCA}(a,\textrm{LCA}(b,c))=\textrm{LCA}(\textrm{LCA}(a,b),c)

LCA 求路径

\textrm{dis}(a,b)=\textrm{dis}(a,root)+\textrm{dis}(b,root)-2 \times \textrm{dis}(\textrm{LCA}(a,b),root)

三点最短路

点

x

使得

\textrm{dis}(a,x)+\textrm{dis}(b,x)+\textrm{dis}(c,x)

最小，则

x

一定是

\textrm{LCA}(a,b)

\textrm{LCA}(b,c)

\textrm{LCA}(a,c)

中深度最深的那个。

判断一点 $C$ 是否经过路径 $A \to B$

若经过，则必须满足其中的至少一个条件：

C=\textrm{LCA}(A,B)

(C=\textrm{LCA}(A,C)) \oplus (C=\textrm{LCA}(B,C))

其中

\oplus

表示异或。

判断路径 $a \to b$ 和 $c \to d$ 是否相交

若相交，则必定满足其中的至少一个条件：

$\textrm{LCA}(a,b)$ 在 $c \to d$ 里；
$\textrm{LCA}(c,d)$ 在 $a \to b$ 里。

Ⅲ. 树上差分

树上差分是“线性差分”在树结构的延伸，核心用于 批量修改路径权值（如路径加值、统计覆盖次数），并通过一次后序遍历快速得到最终结果。其本质是“将路径修改转化为端点修改”，利用树的父子继承关系，避免暴力遍历路径，时间复杂度优化至

\mathcal{O}(n \log n + q)

（

q

为修改次数）。

根据修改对象，树上差分分为 点差分（修改节点权值）和 边差分（修改边权值），核心均依赖 LCA 拆分路径。

1. 点差分（节点路径修改）

适用于“对路径

a \to b

上所有节点加

k

”的批量操作，最终通过前缀和还原每个节点的实际值。

核心修改规则

将路径

a \to b

拆分为

a \to \text{LCA}

和

b \to \text{LCA}

，通过差分数组

\text{diff}_v[]

标记端点：

$\text{diff}_v[a] \leftarrow \text{diff}_v[a]+k$ （起点加值）；
$\text{diff}_v[b] \leftarrow \text{diff}_v[b]+k$ （终点加值）；
$\text{diff}_v[\text{LCA}(a,b)] \leftarrow \text{diff}_v[\text{LCA}(a,b)]-k$ （LCA 被重复加值，抵消一次）；
$\text{diff}_v[\textrm{fa}[\text{LCA}(a,b)]] \leftarrow \text{diff}_v[\textrm{fa}[\text{LCA}(a,b)]]-k$ （LCA 父节点及以上节点不在路径上，抵消误加的影响）。

结果还原（后序遍历前缀和）

修改完成后，通过一次后序 DFS 计算前缀和，得到每个节点的最终权值：

对节点

u

，其最终权值

w_{\text{final}}[u] = \text{diff}_v[u] + \sum\limits_{v \in \text{son}(u)} w_{\text{final}}[v]

。
（子节点的差分影响会向上传递，覆盖整个路径）

2. 边差分（边路径修改）

树的边可唯一对应一个子节点（如边

u \to v

若

u

是父节点，则该边记为“边

v

”），因此边差分可转化为子节点的差分操作。

核心修改规则

对路径

a \to b

上所有边加

k

，差分数组

\text{diff}_e[]

标记规则：

$\text{diff}_e[a] \leftarrow \text{diff}_e[a]+k$ （起点对应的边及以下边加值）；
$\text{diff}_e[b] \leftarrow \text{diff}_e[b]+k$ （终点对应的边及以下边加值）；
$\text{diff}_e[\text{LCA}(a,b)] \leftarrow \text{diff}_e[\text{LCA}(a,b)] - 2k$ （LCA 以下的边被重复加值，抵消两倍）。

结果还原（后序遍历前缀和）

边的最终权值通过后序 DFS 传递，每个子节点的差分影响对应其依附的边：

对节点

v

（对应边

v

），其最终边权

w_{\text{final}}[v] = \text{diff}_e[v] + \sum_{u \in \text{son}(v)} w_{\text{final}}[u]

。

应用场景

点差分：统计多条路径覆盖的节点最大覆盖次数、节点权值的批量更新与单点查询。
边差分：统计多条路径覆盖的边次数、边权的批量更新与查询（如判断某边是否被所有路径覆盖）。

Ⅳ. 三者关联与核心思想

LCA 是基础：树上前缀和的路径和计算、树上差分的路径拆分，均依赖 LCA 确定路径的公共部分，避免暴力遍历。
前缀和是“查询优化”：将路径和查询从 $\mathcal{O}(n)$ 降至 $\mathcal{O}(\log n)$ ，核心是“预处理累积值”。
差分是“修改优化”：将路径修改从 $\mathcal{O}(n)$ 降至 $\mathcal{O}(1)$ （单次修改），核心是“端点标记 + 后序还原”。

三者结合可解决绝大多数树上路径相关问题，是图论中树结构的核心工具组合。

重链剖分

Ⅰ. 重链剖分基础

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。

具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。

重链剖分是如何将树分为不超过

\mathcal{O}(\log n)

条链条的呢？首先，上定义。

对于一棵树，

对于非叶子节点，重子节点表示其子节点中子树最大的子结点中编号最小的那个。
定义轻子节点表示剩余的所有子结点。
从这个结点到重子节点的边为重边。
到其他轻子节点的边为轻边。
若干条首尾衔接的重边构成重链。
把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

好了，比如说看下下面这棵树的剖分方式：

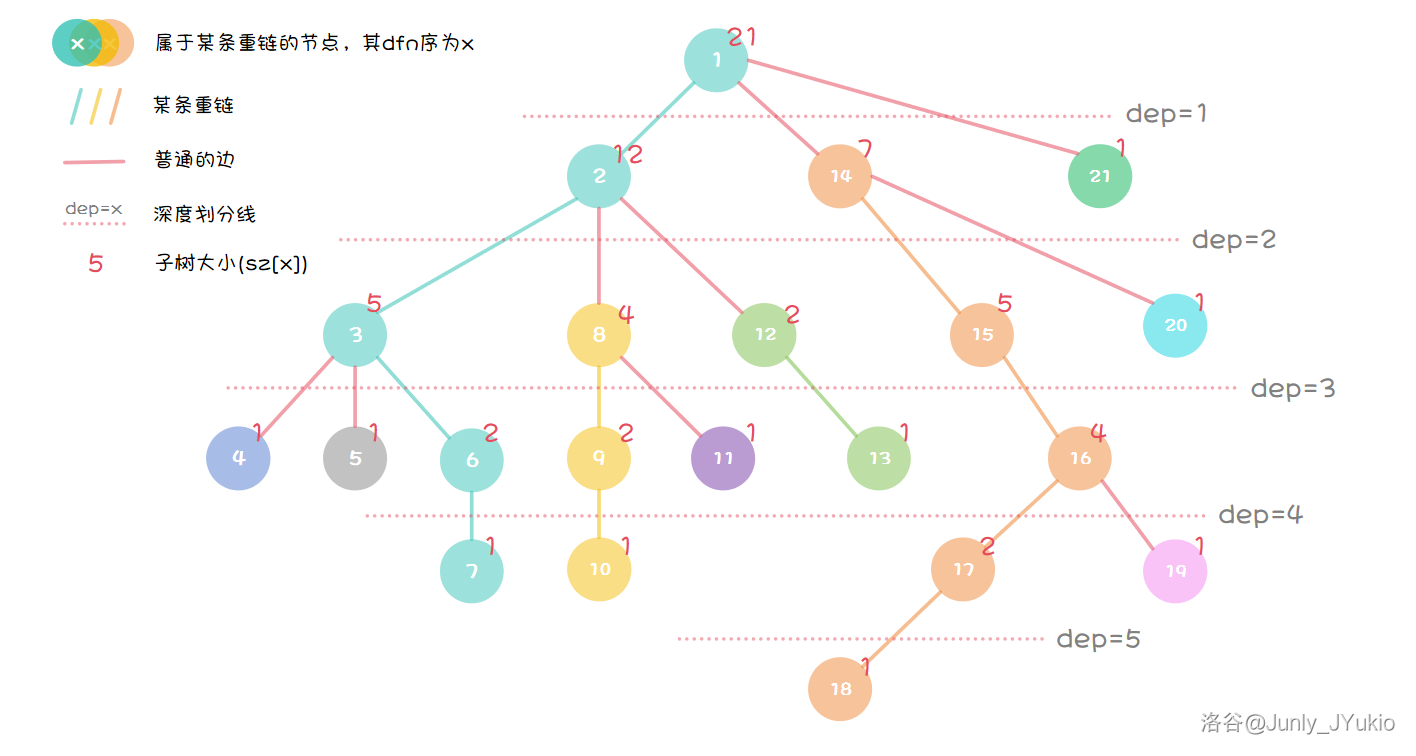
这个时候，姑且将代码实现放在一边，先看树的

\textrm{dfn}

序产生的无与伦比的两个关键性质：

一条重链上的 $\textrm{dfn}$ 序连续；
一棵子树上的 $\textrm{dfn}$ 序也连续。

这意味着，如果要处理树上的子树信息和链条信息，树链剖分绝对是专业对口的。不仅如此，因为

\textrm{dfn}

序连续的特性，还可以考虑用特殊的数据结构优化。

例如，权值树状数组和值域线段树。

而预处理出一堆树链，所需要的操作很简单 —— 是两次 dfs。

第一次 dfs，所求即为

x

的深度、子树大小、重儿子编号和父节点编号。这很简单。

第二次 dfs，在知道了重儿子编号的基础上，我们可以迅速求出许多更有用的信息，譬如这条重链的顶点，就可以在接下来的代码中一次跳很多格。而其任务简化后非常明确：求出任意节点

x

的所在重链顶点，和

\textrm{dfn}

序。

CPP

inline void dfs(int x,int f) {
	a[x].fa=f,a[x].sz=1,a[x].dep=a[f].dep+1,a[x].son=-1;
	int maxn=-1; // 代表当前最大的子树大小
	for(int i=0; i<vec[x].size(); i++) {
		int y=vec[x][i];
		if(y==f) continue;
		dfs(y,x);
		a[x].sz+=a[y].sz;
		if(a[y].sz>maxn) {
			maxn=a[y].sz;
			a[x].son=y;
		}
	}
}
inline void get(int x,int num) { // 此处的 num 是当前 x 所在重链的顶端节点
	a[x].top=num,a[x].dfn=++idy; // 更新顶端
	rnk[idy]=x;
	if(a[x].son==-1) return;
	get(a[x].son,num);
	for(int i=0; i<vec[x].size(); i++) {
		int y=vec[x][i];
		if(y==a[x].fa or y==a[x].son) continue;
		get(y,y);
	}
}

这么做，还产生了更多巧妙的性质，在做题的时候就可以加以应用了。

树上每个节点都属于且仅属于一条重链。
所有的重链将整棵树完全剖分。
在剖分时重边优先遍历，最后树的 DFS 序上，重链内的 DFS 序是连续的。按 DFN 排序后的序列即为剖分后的链。

因此，对于树上的任意一条路径，把它拆分成从 LCA 分别向两边往下走，分别最多走

\mathcal{O}(\log n)

次，因此，树上的每条路径都可以被拆分成不超过

\mathcal{O} (\log n)

条重链。加上重链上连续序号的性质，我们便能迅速维护链上信息。

Ⅱ. 重链剖分的应用

板子题：应用重链剖分。

重链剖分的核心价值的是利用

\textrm{dfn}

序“连续”的特性，将树的路径、子树转化为线性区间，再结合线段树、树状数组等数据结构，高效处理 路径查询/修改、子树查询/修改 两类核心问题。其应用均围绕“跳重链”思想展开，单次操作时间复杂度为

\mathcal{O}(\log^2 n)

（含数据结构操作），能适配大规模数据场景。

1. 求最近公共祖先（LCA）

重链剖分可独立实现 LCA 求解，核心逻辑是“跳重链至同一条链”，步骤简洁且效率稳定。

核心原理：两点向上跳重链时，优先跳顶端深度更大的链，直到两点处于同一条重链；此时深度较小的节点即为 LCA。
实现代码：

CPP

inline int lca(int u,int v) {
	while(arr[u].top!=arr[v].top) {
		if(arr[arr[u].top].dep<arr[arr[v].top].dep)swap(u,v);
		u=arr[arr[u].top].f;
	}
	return arr[u].dep<arr[v].dep ? u : v;
}

优势：无需额外预处理倍增数组，与剖分过程自然融合，代码复用性高。

2. 路径信息维护

适用于“路径区间加值、路径区间求和/最大值/最小值”等操作，核心是将路径拆分为若干条重链，通过数据结构批量处理连续区间。

核心步骤：
1. 若两点不在同一条重链，先处理顶端深度更大的链（区间为顶端 $\textrm{dfn}$ 至当前节点 $\textrm{dfn}$ ）；
2. 两点跳至同一条重链后，处理剩余区间（深度较小节点 $\textrm{dfn}$ 至深度较大节点 $\textrm{dfn}$ ）；
3. 结合线段树 / 树状数组完成区间修改或查询。
典型操作代码：路径区间加值（结合线段树）：

CPP

inline void update_path(int x,int y,int k) {
	while(arr[x].top!=arr[y].top) {
		if(arr[arr[x].top].dep<arr[arr[y].top].dep)swap(x,y);
		modify(1,1,n,arr[arr[x].top].dfn,arr[x].dfn,k);
		x=arr[arr[x].top].f;
	}
	if(arr[x].dep>arr[y].dep)swap(x,y);
	modify(1,1,n,arr[x].dfn,arr[y].dfn,k);
}

路径区间求和（结合线段树）：

CPP

inline int query_path(int x,int y) {
	int res=0;
	while(arr[x].top!=arr[y].top) {
		if(arr[arr[x].top].dep<arr[arr[y].top].dep)swap(x,y);
		res=(res+query(1,1,n,arr[arr[x].top].dfn,arr[x].dfn))% Mod;
		x=arr[arr[x].top].f;
	}
	if(arr[x].dep>arr[y].dep)swap(x,y);
	return(res+query(1,1,n,arr[x].dfn,arr[y].dfn))% Mod;
}

3. 子树信息维护

由于子树的

\textrm{dfn}

序连续（区间为

\text{dfn}[u] \sim \text{dfn}[u] + \text{sz}[u] - 1

），可直接通过数据结构完成子树的批量修改与查询。

核心原理：子树大小 $\text{sz}[u]$ 决定了子树对应的 $\textrm{dfn}$ 区间长度，无需跳重链，直接定位区间即可。
典型操作代码：
子树区间加值：

CPP

inline void update_subtree(int u,int k) {
    modify(1,1,n,arr[u].dfn,arr[u].dfn+arr[u].sz-1,k);
}

子树区间求和：

CPP

inline int query_subtree(int u) {
    return query(1,1,n,arr[u].dfn,arr[u].dfn+arr[u].sz-1)%Mod;
}

这份代码适配“路径加、路径查、子树加、子树查”四类操作，是重链剖分的经典应用模板。

代码

CPP

#include<cstdio>
int s;
char ch;
inline int read() {
	s=0;
	while((ch=getchar_unlocked())<48);
	do s=(s<<3)+(s<<1)+(ch^48);
	while((ch=getchar_unlocked())>47);
	return s;
}
inline void write(int x) {
	if(x>9) write(x/10);
	putchar(x%10+48);
}
struct node {
	int val,dfn,f,sz,dep,hson,top;
} arr[100002];
int n,T,root,Mod,fr,to,num,rnk[100002];
long long sum[400002],tag[400002];
int head[100002],ver[200002],ne[200002],tot,item;
inline void add(int x,int y) {
	ver[++tot]=y;
	ne[tot]=head[x];
	head[x]=tot;
}
inline void dfs_first(int x,int fa) {
	arr[x].f=fa;
	arr[x].dep=arr[fa].dep+1;
	arr[x].sz=1;
	int max_size=-1;
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(y==fa) continue;
		dfs_first(y,x);
		arr[x].sz+=arr[y].sz;
		if(arr[y].sz>max_size) {
			max_size=arr[y].sz;
			arr[x].hson=y;
		}
	}
}
inline void dfs_second(int x,int now_top) {
	arr[x].dfn=++num;
	rnk[num]=arr[x].val;
	arr[x].top=now_top;
	if(!arr[x].hson) return;
	dfs_second(arr[x].hson,now_top);
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(y==arr[x].f or y==arr[x].hson) continue;
		dfs_second(y,y);
	}
}
inline void build(int p,int l,int r) {
	tag[p]=0;
	if(l==r) {
		sum[p]=rnk[l];
		return;
	}
	int mid=l+r>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	sum[p]=(sum[p<<1]+sum[p<<1|1])%Mod;
}
inline void pushdown(int p,int l,int r) {
	if(!tag[p]) return;
	int lc=p<<1,rc=p<<1|1,mid=l+r>>1;
	tag[lc]=(tag[lc]+tag[p])%Mod;
	tag[rc]=(tag[rc]+tag[p])%Mod;
	sum[lc]=(sum[lc]+(tag[p]*(mid-l+1))%Mod)%Mod;
	sum[rc]=(sum[rc]+(tag[p]*(r-mid))%Mod)%Mod;
	tag[p]=0;
}
inline void modify(int p,int l,int r,int s,int t,int cc) {
	if(s<=l and r<=t) {
		sum[p]=(sum[p]+(cc*(r-l+1))%Mod)%Mod;
		tag[p]=(tag[p]+cc)%Mod;
		return;
	}
	pushdown(p,l,r);
	int mid=l+r>>1;
	if(s<=mid) modify(p<<1,l,mid,s,t,cc);
	if(t>mid) modify(p<<1|1,mid+1,r,s,t,cc);
	sum[p]=(sum[p<<1]+sum[p<<1|1])%Mod;
}
inline long long query(int p,int l,int r,int s,int t) {
	if(s<=l and r<=t) return sum[p];
	pushdown(p,l,r);
	int mid=l+r>>1;
	long long result=0;
	if(s<=mid) result=query(p<<1,l,mid,s,t);
	if(t>mid) result=(result+query(p<<1|1,mid+1,r,s,t))%Mod;
	return result;
}
inline void update(int x,int y,int k) {
	while(arr[x].top!=arr[y].top) {
		if(arr[arr[x].top].dep<arr[arr[y].top].dep) {item=x;x=y;y=item;}
		modify(1,1,n,arr[arr[x].top].dfn,arr[x].dfn,k);
		x=arr[arr[x].top].f;
	}
	if(arr[x].dep>arr[y].dep) {item=x;x=y;y=item;}
	modify(1,1,n,arr[x].dfn,arr[y].dfn,k);
}
inline int ask(int x,int y) {
	int ans=0;
	while(arr[x].top!=arr[y].top) {
		if(arr[arr[x].top].dep<arr[arr[y].top].dep) {item=x;x=y;y=item;}
		ans=(ans+query(1,1,n,arr[arr[x].top].dfn,arr[x].dfn))%Mod;
		x=arr[arr[x].top].f;
	}
	if(arr[x].dep>arr[y].dep) {item=x;x=y;y=item;}
	return (ans+query(1,1,n,arr[x].dfn,arr[y].dfn))%Mod;
}
int opt,qx,qy;
int main() {
	n=read(), T=read(), root=read(), Mod=read();
	for(int i=1; i<=n; i++) arr[i].val=read();
	for(int i=1; i<n; i++) {
		fr=read(), to=read();
		add(fr,to);
		add(to,fr);
	}
	dfs_first(root,0);
	dfs_second(root,root);
	build(1,1,n);
	while(T--) {
		opt=read(), qx=read();
		if(opt==1) {
			qy=read();
			update(qx,qy,read());
		} else if(opt==2) {
			write(ask(qx,read()));
			putchar('\n');
		} else if(opt==3) {
			modify(1,1,n,arr[qx].dfn,arr[qx].dfn+arr[qx].sz-1,read());
		} else {
			write(query(1,1,n,arr[qx].dfn,arr[qx].dfn+arr[qx].sz-1));
			putchar('\n');
		}
	}
	return 0;
}

差分约束

差分约束问题通常进行在一个神秘的不等式方程组内，其往往需要协调较多的内容，如果不建模为图上信息的互相制约，恐怕很难进行处理。

差分约束系统由一组 线性不等式约束 构成，所有约束均围绕两个变量的差值与常数的关系展开。设

x_1, x_2, ..., x_n

为

n

个变量，约束的标准形式分为两类：

上界约束： $x_i - x_j \leq c$ （ $x_i$ 与 $x_j$ 的差值不超过常数 $c$ ）
下界约束： $x_i - x_j \geq c$ （ $x_i$ 与 $x_j$ 的差值不小于常数 $c$ ）

其中

c

是已知常数，

i, j \in \{1, 2, ..., n\}

。我们的目标是找到一组满足所有约束的变量值（可行解），或判断系统无解。

板子题。
该问题的基础版本是：给定 $c_1 \sim s_m$ ，你需要找出任意一组 $x_1,x_2,\cdots,x_n$ ，满足： $\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases}$ 若无解，请输出 NO。 $n,m \le 5 \times 10^3$ ， $c_i \neq c'_i$ 。

首先，需要将该题目抽象成图上问题。差分约束的本质是“将不等式转化为路径关系”，这一转化源于最短路径 / 最长路径的松弛特性 —— 不等式的结构与路径长度的约束完全等价。

考虑上界约束

x_i - x_j \le c

，对其进行等价变形，即可变为

x_i \le x_j + c

。这与图论中 最短路径的松弛条件 高度契合：

在有向图中，若存在边 $j\rightarrow i$ ，权值为 $c$ ，则节点 $i$ 的最短路径长度 $d_i$ 满足 $d_i\leq d_j+c$ 。

由此建立映射规则：

每个变量 $x_k$ 对应图中的一个节点 $k$ ；
约束 $x_i - x_j \leq c$ 对应图中一条 从 $j$ 到 $i$ 、权值为 $c$ 的有向边。

同理，如果要考虑下界约束

x_i-x_j \ge c

，就只需要建立一条从

i

到

j

的，权值为

c

的边即可。

转化为图之后又怎么做呢？

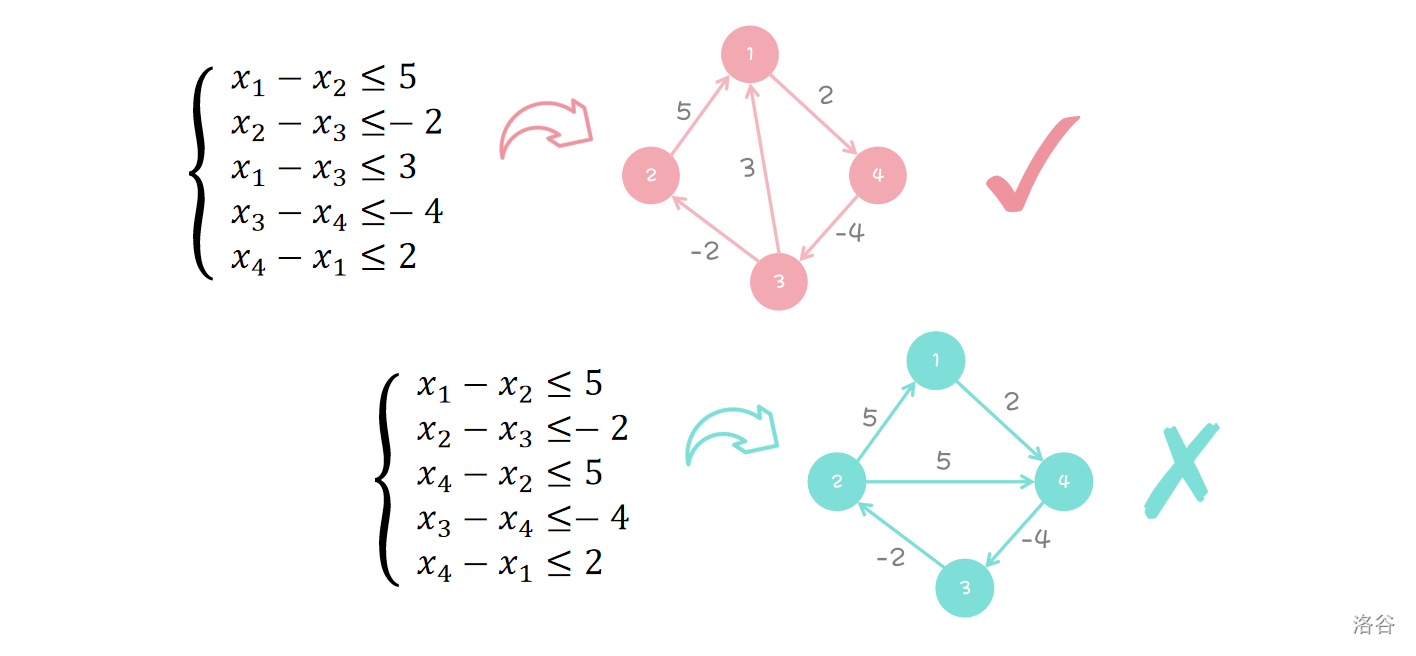
在图中，我们发现上面的部分存在解，而下面的部分无解。

推导

\because x_2-x_3 \le -2

\therefore x_2 \le x_3 -2~~~~~~~~~~(1)

\because x_4-x_2 \le 5

\therefore x_2 \ge x_4-5~~~~~~~~~~(2)

\because x_3-x_4 \le -4

\therefore x_3 = x_4-4-k (k \in \mathbb{N})~~~~~~~~~(3)

代入得：

x_4-5 \le x_2 \le x_4-6-k(k \in \mathbb{N})

矛盾。

故原方程无解。

我们可以发现，可以推出矛盾的若干个变量必须在其建立的图上构成一个环，并且该环使用代入法绕一圈回来后将会出现矛盾。推导后不难发现，

x \le x+k

就是该环能够成立的条件，其中

k

就是该环的权值之和。显然，负环上，原不等式方程无解。否则，将图扫一遍，每个节点都附最短路的权值（即

x_i=\textrm{dis}_i

）就是原方程的一组解。

负环判定回顾

负环判定可以使用优化过的 spfa 或 bellman-ford 算法进行优化。只要经过足量的扩展后，仍然存在能够优化的点，就说明图中存在负环。下面 AC 了板子题的代码使用了朴素 bellman-ford 来进行计算，最坏时间复杂度

\Omega(T \times n \times m)

。

CPP

#include<bits/stdc++.h>
#define F first
#define S second
#define PII pair<int,int>
using namespace std;
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
int f;
template<typename _Tp>
inline void read(_Tp& x) {
    x=0, f=1;
    do if(ch=='-') f=-1;
    while((ch=gc())<48);
    do x=(x<<3)+(x<<1)+(ch^48);
    while((ch=gc())>47);
    x*=f;
}
vector<PII> vec[2002];
int n,m,T,fr,to,wi,dis[2002];
bool bell;
inline void eat(){
	read(n), read(m);
    for(int i=1; i<=n; i++) vec[i].clear();
	for(int i=1; i<=m; i++){
		read(fr), read(to), read(wi);
		vec[fr].push_back({to,wi});
		if(wi>=0) vec[to].push_back({fr,wi});
	} 
	for(int i=1; i<=n; i++) dis[i]=2e9;
	dis[1]=0;
	for(int i=1; i<n; i++){
		bell=0;
		for(int j=1; j<=n; j++){
			if(dis[j]==2e9) continue;
			for(PII k:vec[j]) if(dis[k.F]>dis[j]+k.S){dis[k.F]=dis[j]+k.S;bell=1;}
		}
		if(!bell) break;
	}
	bell=0;
	for(int j=1; j<=n; j++){
		if(dis[j]==2e9) continue;
		for(PII k:vec[j]) if(dis[k.F]>dis[j]+k.S){dis[k.F]=dis[j]+k.S;bell=1;}
		if(bell) break;
	}
	bell ? puts("YES") : puts("NO");
}
int main(){
	read(T);
	while(T--) eat();
	return 0;
}

下面给出板子题的代码，这里建议建造一个虚点

0

，将其与所有其它点连一条单向权

0

边。

代码

CPP

#include<bits/stdc++.h>
#define F first
#define S second
#define PII pair<int,int>
using namespace std;
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
int f;
template<typename _Tp>
inline void read(_Tp& x) {
	x=0, f=1;
	do if(ch=='-') f=-1;
	while((ch=gc())<48);
	do x=(x<<3)+(x<<1)+(ch^48);
	while((ch=gc())>47);
	x*=f;
}
template<typename _Tp>
inline void write(_Tp x) {
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar((x%10)^48);
}
vector<PII> vec[5002];
int n,m,fr,to,wi,dis[5002];
bool bell;
int main() {
	read(n), read(m);
	for(int i=1; i<=m; i++) {
		read(fr), read(to), read(wi);
		vec[to].push_back({fr,wi});
	}
	for(int i=1; i<=n; i++) vec[0].push_back({i,0}),dis[i]=2e9;
	dis[0]=0;
	for(int i=1; i<=n; i++) {
		bell=0;
		for(int j=0; j<=n; j++) {
			if(dis[j]==2e9) continue;
			for(PII k:vec[j]) if(dis[k.F]>dis[j]+k.S) {
					dis[k.F]=dis[j]+k.S;
					bell=1;
				}
		}
		if(!bell) break;
	}
	bell=0;
	for(int j=1; j<=n; j++) {
		if(dis[j]==2e9) continue;
		for(PII k:vec[j]) if(dis[k.F]>dis[j]+k.S) {
				dis[k.F]=dis[j]+k.S;
				bell=1;
			}
		if(bell) break;
	}
	if(bell){
		puts("NO");
		return 0;
	}
	for(int i=1; i<=n; i++) write(dis[i]),putchar(' ');
	return 0;
}

Tarjan 算法

Ⅰ. $\textrm{dfn}$ 序和 $\textrm{low}$ 数组

Tarjan 算法的核心是通过深度优先搜索（DFS）维护两个关键数组，用于刻画节点的访问次序与回溯关系：

$\textrm{dfn}_u$ ：节点 $u$ 被首次访问的时间戳（访问次序），具有唯一性；
$\textrm{low}_u$ ：节点 $u$ 及其子树中能回溯到的最早时间戳（即通过一条回边可到达的最浅祖先的 $\textrm{dfn}$ ）。

这样一来，Tarjan 算法将一个树从图中抽离出来，并将图中的边分为了四等：

树边：第一次遍历需要经过的边 / 搜索树上的边。
返祖边：从一个点指向其祖先的边。
横叉边：从一个点指向比其先遍历的边。
前向边：从一个点指向其子树中儿子的边，且其儿子已经被更新过了。

看一张图。

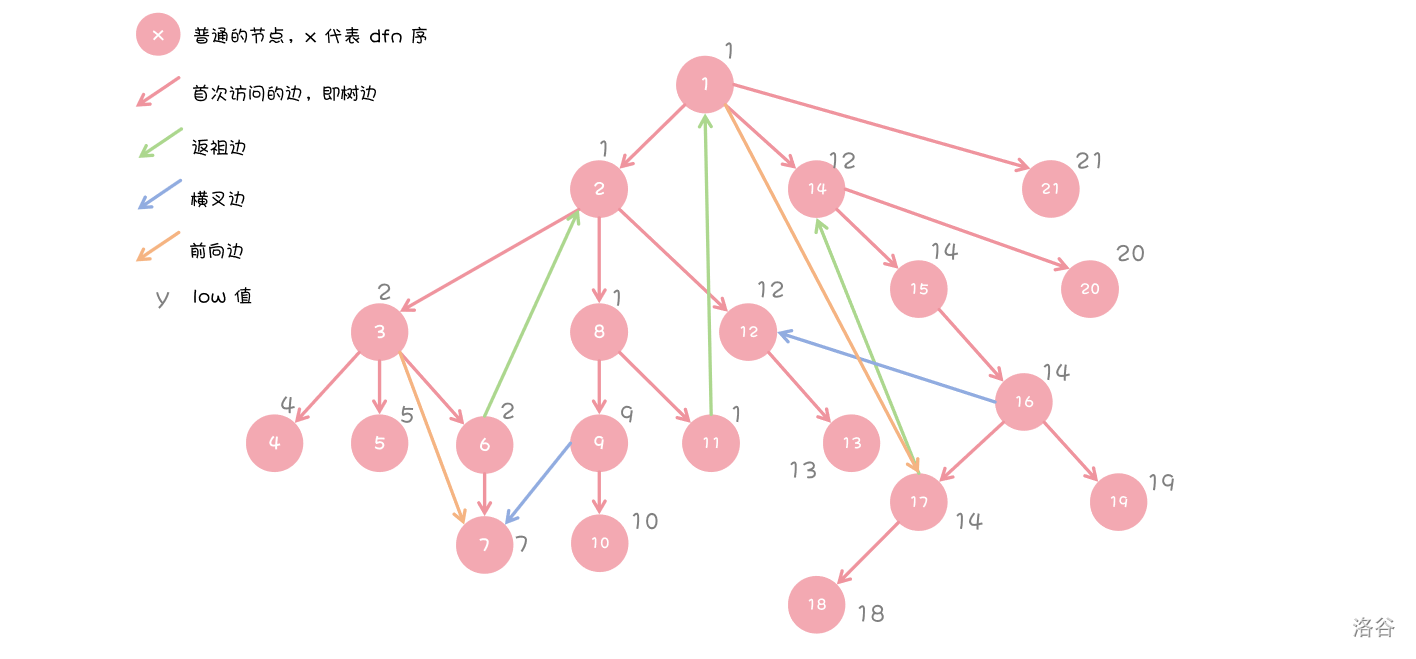
通过图片也不难发现，

\textrm{low}

值的计算主要是和元素是否在栈内密切相关。

如图，唯二对

\textrm{low}

值做出贡献的，就是返祖边和前向边。

二者的更新规则：

首次访问 $u$ 时，初始化 $\textrm{dfn}_u = \textrm{low}_u = \textrm{tim}$ ，且 $\textrm{tim} \leftarrow \textrm{tim}+1$ ；
遍历邻接节点 $v$ $v$ ：
- 若 $v$ 未访问：递归访问 $v$ ，回溯后更新 $\textrm{low}_u = \min(\textrm{low}_u, \textrm{low}_v)$ ；
- 若 $v$ 已访问且未出栈（无向图中排除父节点）：更新 $\textrm{low}_u = \min(\textrm{low}_u, \textrm{dfn}_v)$ 。

这两个数组是识别连通分量、桥、割点的基础，时间复杂度为

\mathcal{O}(n+m)

。

Ⅱ. 强连通分量（SCC）

强连通分量是有向图中“任意两点互达”的极大子图（即一大堆环），Tarjan 算法通过栈维护未确定分量的节点，结合

\textrm{dfn}

与

\textrm{low}

数组识别 SCC。

核心原理

用栈存储当前 DFS 树中访问过的节点；
当 $\textrm{dfn}_u = \textrm{low}_u$ 时， $u$ 为当前 SCC 的根节点，将栈中 $u$ 及其上方节点弹出，构成一个 SCC。

核心实现代码

CPP

inline void tarjan(int x) {
    dfn[x]=low[x]=++cur;
    st[++top]=x,vis[x]=1;
    for(int i=0; i<vec[x].size(); i++) {
        int y=vec[x][i];
        if(!dfn[y]) {
            tarjan(y);
            if(low[y]<low[x]) low[x]=low[y];
        } else if(vis[y] and dfn[y]<low[x]) low[x]=dfn[y];
    }
    if(low[x]==dfn[x]) {
        cnt++;
        while(true) {
            z=st[top--];
            vis[z]=0;
            scc[z]=cnt;
            sz[cnt]+=a[z];
            if(x==z) break;
        }
    }
}

应用场景

缩点：将每个 SCC 视为单个节点，转化为 DAG 后求解最长路、可达性等问题；
解决强连通相关约束问题，如判断两点是否互达。

Ⅲ. 边双连通分量（E - DCC）

边双连通分量是无向图中“去掉任意一条边仍连通”的极大子图，其核心是识别“桥”（去掉后图连通性改变的边），去掉所有桥后剩余的连通分量即为 E - DCC。

核心原理

桥的判定：对于无向边 $u-v$ ，若 $\textrm{low}_v > \textrm{dfn}_u$ ，则该边为桥（ $v$ 无法通过其他路径回溯到 $u$ 的祖先）；
遍历所有边，去掉桥后对图进行连通性分析，每个连通块即为 E - DCC。

板子代码

CPP

#include<cstdio>
#include<vector>
#define N 500002
#define M 4000002
using std::vector;
int s,f;
char ch;
inline int read(){
	s=0, f=1;
	do if(ch=='-') f=-1;
	while((ch=getchar())<48);
	do s=(s<<3)+(s<<1)+(ch^48);
	while((ch=getchar())>47);
	return s*f;
}
inline void write(int x){
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+48);
}
int head[N],ver[M],ne[M],tot=1,b[M];
inline void add(int x,int y){
	ver[++tot]=y;
	ne[tot]=head[x], head[x]=tot;
}
bool bl[M];
int n,m,dfn[N],low[N],cur,u,v,edcc;
inline void tarjan(int x,int fa_E){
	dfn[x]=low[x]=++cur;
	for(int i=head[x]; i; i=ne[i]){
		if(i==fa_E) continue;
		int y=ver[i];
		if(!dfn[y]){
			tarjan(y,i^1);
			if(dfn[x]<low[y]) bl[i]=bl[i^1]=1;
			if(low[x]>low[y]) low[x]=low[y];
		}else if(dfn[y]<low[x]) low[x]=dfn[y];
	}
}
bool vis[N];
vector<int> E[N];
inline void paint(int x){
	E[edcc].push_back(x); 
	vis[x]=1;
	for(int i=head[x]; i; i=ne[i]){
		int y=ver[i];
		if(vis[y] or bl[i]) continue;
		paint(y);
	}
}
int main(){
	n=read(), m=read();
	for(int i=1; i<=m; i++){
		u=read(), v=read();
		add(u,v);
		add(v,u); 
	}
	for(int i=1; i<=n; i++){
		if(!dfn[i]) tarjan(i,-1);
	}
	for(int i=1; i<=n; i++){
		if(!vis[i]){
			++edcc;
			paint(i);
		}
	}
	write(edcc);
	putchar('\n');
	for(int i=1; i<=edcc; i++){
		write(E[i].size());
		for(int j=0; j<E[i].size(); j++) putchar(' '),write(E[i][j]);
		putchar('\n');
	}
	return 0;
}

Ⅳ. 点双连通分量（V - DCC）

点双连通分量是无向图中“去掉任意一个节点仍连通”的极大子图，核心是识别“割点”（去掉后图连通性改变的节点），通过栈存储边来收集 V - DCC。

核心原理

割点判定：
1. 根节点：若有至少 2 个非空子树，则为割点；
2. 非根节点：若存在子节点 $v$ ，使得 $\textrm{low}[v] \geq \textrm{dfn}[u]$ ，则 $u$ 为割点；
用栈存储访问过的边，当遇到割点时，弹出栈中边直至当前边，构成 V - DCC（单个孤立节点也是 V - DCC）。

核心实现代码

CPP

inline void tarjan(int x){
	dfn[x]=low[x]=++cur;
	st[++top]=x;
	if(x==root and head[x]==0){ // 孤立点 
        ++col;
		vec[col].push_back(x);
		return;
	}
	for(int i=head[x]; i; i=ne[i]){
		int y=ver[i];
		if(!dfn[y]){
			tarjan(y);
			if(low[x]>low[y]) low[x]=low[y];
			if(dfn[x]<=low[y]){
				++col;
				while(true){
					int z=st[top--];
					vec[col].push_back(z);
					if(z==y) break;
				}
				vec[col].push_back(x);
			}
		}else if(dfn[y]<low[x]) low[x]=dfn[y];
	}
}

有了这类方法，重在实践的 Tarjan 算法也有了自己的巨大作用。请看后面的例题

5 \sim 7

。

2 - SAT 适应性问题

2 - SAT 问题是图论中处理布尔变量约束满足的核心算法，专门解决变量取值仅为“真”或“假”，且约束为逻辑蕴含式的问题。其核心思想是将布尔变量的逻辑约束转化为有向图的可达性问题，通过 Tarjan 算法求解强连通分量（SCC），进而判定约束是否可满足并给出可行解。

Ⅰ. 核心建模

2 - SAT 的建模是算法的关键，其本质是将布尔逻辑转化为图的边关系，每个变量的两种取值对应图中的两个节点，逻辑约束对应节点间的有向边。

1. 变量与节点映射

每个布尔变量

x_i

对应图中的两个节点，节点编号需简洁且便于计算：

$2 \times i$ ：表示变量 $x_i$ 取值为假（记为 $\neg x_i$ ）；
$2 \times i+1$ ：表示变量 $x_i$ 取值为真（记为 $x_i$ ）。该映射方式确保每个变量的两种状态互不混淆，且节点编号连续，便于数组存储和遍历。例如，变量 $x_1$ 的“假”状态对应节点 $2$ ，“真”状态对应节点 $3$ ；变量 $x_2$ 的“假”状态对应节点 $4$ ，“真”状态对应节点 $5$ ，以此类推。

2. 约束转化逻辑推导

所有逻辑约束均可转化为“蕴含式

a \rightarrow b

”（若

a

为真，则

b

必为真），而蕴含式的图论表达是“从

a

对应的节点向

b

对应的节点连一条有向边”。这是因为在最短路径的松弛逻辑中，边

u \rightarrow v

表示“若

u

可达，则

v

必可达”，与蕴含式的逻辑完全等价。

常见约束的转化方式及推导：

蕴含式约束 $a \rightarrow b$ ：逻辑等价于 $\neg a \lor b$ （ $a$ 为假或 $b$ 为真）。若 $a$ 为真却 $b$ 为假，则约束不满足。因此需建边 $\text{id}(a) \rightarrow \text{id}(b)$ （ $a$ 为真时强制 $b$ 为真），同时建边 $\text{id}(\neg b) \rightarrow \text{id}(\neg a)$ （ $b$ 为假时强制 $a$ 为假），二者缺一不可。
矛盾约束 $a \land b = \text{false}$ ：表示 $a$ 和 $b$ 不能同时为真，等价于 $a \rightarrow \neg b$ 且 $b \rightarrow \neg a$ 。建边 $\text{id}(a) \rightarrow \text{id}(\neg b)$ 和 $\text{id}(b) \rightarrow \text{id}(\neg a)$ ，确保若其中一个为真，另一个必为假。
等价约束 $a = b$ ：表示 $a$ 和 $b$ 取值相同，等价于 $a \rightarrow b$ 且 $b \rightarrow a$ 。建边 $\text{id}(a) \rightarrow \text{id}(b)$ 、 $\text{id}(b) \rightarrow \text{id}(a)$ 、 $\text{id}(\neg a) \rightarrow \text{id}(\neg b)$ 、 $\text{id}(\neg b) \rightarrow \text{id}(\neg a)$ ，覆盖“同真”和“同假”两种情况。
选择约束 $a \lor b = \text{true}$ ：表示 $a$ 和 $b$ 至少一个为真，等价于 $\neg a \rightarrow b$ 且 $\neg b \rightarrow a$ 。建边 $\text{id}(\neg a) \rightarrow \text{id}(b)$ 和 $\text{id}(\neg b) \rightarrow \text{id}(a)$ ，确保若其中一个为假，另一个必为真。

Ⅱ. 可行性判定与求解逻辑

建模完成后，通过 Tarjan 算法求解图的强连通分量（SCC），即可完成约束满足的判定和可行解的构造。

1. 可行性判定原理

若存在某个变量

x_i

，其对应的两个节点（

2 \times i

和

2 \times i+1

）属于同一个 SCC，则约束系统无解。
原因：同一 SCC 中的节点相互可达，意味着“

x_i

为真”可推出“

x_i

为假”，同时“

x_i

为假”可推出“

x_i

为真”，逻辑矛盾，故无解。

2. 可行解构造逻辑

若系统有解，对于每个变量

x_i

，需选择其两个节点所在 SCC 中“拓扑序更靠前”的节点对应的取值。由于 Tarjan 算法求解 SCC 时，栈弹出的顺序与 SCC 的拓扑序相反（后弹出的 SCC 拓扑序更靠前），因此：

比较 $\text{col}[2 \times i]$ （ $\neg x_i$ 所在 SCC 的编号）和 $\text{col}[2 \times i+1]$ （ $x_i$ 所在 SCC 的编号）；
若 $\text{col}[2 \times i+1] < \text{col}[2 \times i]$ ，则 $x_i$ 取真（因 $x_i$ 所在 SCC 拓扑序更靠前，优先级更高）；
反之， $x_i$ 取假。

该选择逻辑确保所有约束均被满足，因为拓扑序靠前的 SCC 不会被后续 SCC 推出矛盾。例如，若

\text{col}[3] < \text{col}[2]

，则

x_1

取真，此时所有从节点 3 出发的边对应的约束（如

x_1 \rightarrow x_2

）均会因节点 3 可达而强制后续节点（如 5）对应的状态（

x_2

真）生效。

代码

CPP

#include<cstdio>
#define For(i,a,b) for(register int i=a; i<=b; ++i)
#define N 2000002
//#pragma GCC optimize("Ofast") 
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
template<typename _Tp>
inline void read(_Tp& x) {
    x=0;
    while((ch=gc())<48);
    do x=(x<<3)+(x<<1)+(ch^48);
    while((ch=gc())>47);
}
int head[N],ne[N],ver[N],tot;
inline void add(int x,int y){
	ver[++tot]=y;
	ne[tot]=head[x], head[x]=tot;
}
int n,m,aa,bb,cc,dd,dfn[N],low[N],num,st[N],scc[N],top,cnt,z;
inline void tarjan(int x){
	low[x]=dfn[x]=++num;
	st[++top]=x;
	for(int i=head[x]; i; i=ne[i]){
		int y=ver[i];
		if(!dfn[y]){
			tarjan(y);
			if(low[y]<low[x]) low[x]=low[y];
		}else if(!scc[y] and dfn[y]<low[x]) low[x]=dfn[y];
	}
	if(low[x]==dfn[x]){
		++cnt;
		while(true){
			z=st[top--];
			scc[z]=cnt;
			if(z==x) break;
		}
	}
}
int main(){
	read(n), read(m);
	For(i,1,m){
		read(aa), read(bb), read(cc), read(dd);
		add(aa+(bb^1)*n,cc+dd*n);
		add(cc+(dd^1)*n,aa+bb*n);
	}
	For(i,1,n){
		if(!dfn[i]) tarjan(i);
		if(scc[i]==scc[i+n]){
			puts("IMPOSSIBLE");
			return 0;
		}
	}
	For(i,n+1,(n<<1)){
		if(!dfn[i]) tarjan(i);
	}
	// 接下来注定有解 
	puts("POSSIBLE");
	For(i,1,n){
		putchar((scc[i+n]<scc[i])+48), putchar(' ');
	}
	return 0;
}

二分图基础

Ⅰ. 二分图的定义与判定

定义

二分图是顶点可划分为两个互不相交的集合

U

和

V

，且所有边仅存在于

U

与

V

之间的无向图（无奇数长度的环）。

二分图非常类似于“连线题”，只有左边连右边或者右边连左边，不能自己连自己。因此，二分图有非常多美丽的性质。

比如，二分图没有奇数大小的环。

判定算法（染色法）

核心思想：用两种颜色对顶点染色，相邻顶点颜色不同则为二分图；
实现：DFS 或 BFS 遍历，初始顶点染颜色 1，邻接顶点染相反颜色，若冲突则非二分图。

核心实现代码

CPP

inline bool dfs(int u,int c) {
    col[u]=c;
    for(int v:h[u]) {
        if(!col[v]) {
            if(!dfs(v,3-c)) return 0;
        }else if(col[v]==c) return 0;
    }
    return 1;
}

Ⅱ. 二分图最大匹配

1. 匹配相关定义

匹配：设二分图 $G=(U, V, E)$ ，匹配 $M$ 是 $E$ 的子集，且 $M$ 中任意两条边无公共顶点。例如，边集 $\{(u_1,v_1), (u_2,v_2)\}$ 是匹配，但若存在边 $(u_1,v_2)$ 则不可加入（与 $(u_1,v_1)$ 共享 $u_1$ ）；
最大匹配：边数最多的匹配，记为 $|M|_{\text{max}}$ ；
完美匹配：若 $|U| = |V| = |M|_{\text{max}}$ ，则匹配 $M$ 为完美匹配（所有顶点均被匹配）；
增广路：起点和终点均为未匹配顶点，且匹配边与非匹配边交替出现的路径。例如，路径 $u_0$ （未匹配）→ $v_1$ （匹配）→ $u_1$ （匹配）→ $v_0$ （未匹配）是增广路，反转路径中的边（匹配边变非匹配，非匹配边变匹配）可使匹配边数增加 1。

2. 匈牙利算法（求最大匹配）

匈牙利算法是求解二分图最大匹配的经典算法，核心思想是“不断寻找增广路并更新匹配”，直到无法找到新的增广路为止。

（1）算法步骤（以 $U$ 为左集合， $V$ 为右集合为例）

初始化匹配数组 $\text{match}$ ， $\text{match}[v] = 0$ 表示右集合顶点 $v$ 未匹配；
遍历左集合的每个顶点 $u$ $u$ ：
- 初始化访问数组 $\text{vis}$ （标记右集合顶点是否已被尝试匹配，避免重复访问）；
- 调用 DFS 寻找以 $u$ $u$ 为起点的增广路：
  - 对 $u$ $u$ 的每个邻接顶点 $v$ $v$ ，若 $v$ $v$ 未访问：
    - 标记 $v$ 为已访问；
    - 若 $v$ 未匹配，或 $v$ 的匹配顶点 $\text{match}[v]$ 可找到新的增广路，则将 $u$ 与 $v$ 匹配（更新 $\text{match}[v] = u$ ），返回成功（找到增广路）；
遍历结束后， $\text{match}$ 数组中非零元素的个数即为最大匹配数。

匈牙利算法

核心思想：对每个顶点尝试寻找增广路，若找到则更新匹配；
时间复杂度： $\mathcal{O}(nm)$ ，适用于中小规模数据。

实现代码

CPP

#include<cstdio>
int s;
char ch;
inline int read(){
    s=0;
    while((ch=getchar())<48);
    do s=(s<<3)+(s<<1)+(ch^48);
    while((ch=getchar())>47);
    return s;
}
int n,m,e;
int head[1002],ver[50002],ne[50002],tot,tim,vis[1002],tag[1002],ans;
inline void add(int x){
	ver[++tot]=read()+n;
	ne[tot]=head[x], head[x]=tot;
}
inline bool dfs(int x){
	for(int i=head[x]; i; i=ne[i]){
		int y=ver[i];
		if(vis[y]==tim) continue;
		vis[y]=tim;
		if(!tag[y] or dfs(tag[y])){
			tag[y]=x;
			return 1;
		}
	}
	return 0;
}
int main(){
	n=read(), m=read(), e=read();
	for(int i=1; i<=e; i++) add(read());
	for(int i=1; i<=n; i++){
		tim++;
		ans+=dfs(i);
	}
	printf("%d",ans);
	return 0;
}

Ⅲ. 二分图最大独立集与最小点覆盖

1. 核心定义

独立集：设图 $G=(V,E)$ ，独立集 $S$ 是 $V$ 的子集，且 $S$ 中任意两个顶点无公共边（即无相邻顶点）。最大独立集是顶点数最多的独立集，记为 $|S|_{\text{max}}$ ；
点覆盖：设图 $G=(V,E)$ ，点覆盖 $T$ 是 $V$ 的子集，且 $G$ 中所有边均至少有一个端点属于 $T$ （即覆盖所有边）。最小点覆盖是顶点数最少的点覆盖，记为 $|T|_{\text{min}}$ 。

2. Konig 定理（二分图特有）

Konig 定理是二分图的核心定理，建立了最大匹配、最大独立集与最小点覆盖之间的关系：

定理 1：二分图的最小点覆盖顶点数 = 最大匹配数，即 $|T|_{\text{min}} = |M|_{\text{max}}$ ；
定理 2：二分图的最大独立集顶点数 = 总顶点数 - 最大匹配数，即 $|S|_{\text{max}} = |U| + |V| - |M|_{\text{max}}$ 。

证明

必要性：设最大匹配为 $M$ ，总顶点数为 $N = |U| + |V|$ 。由于最大独立集 $S$ 中无相邻顶点，故 $S$ 中最多包含 $M$ 条匹配边中的 $M$ 个顶点（每条匹配边选一个），剩余 $N - 2M$ 个顶点可全部加入 $S$ ，因此 $|S| \leq M + (N - 2M) = N - M$ ；
充分性：通过构造可证明存在独立集 $S$ 满足 $|S| = N - M$ 。例如，从最大匹配 $M$ 出发，标记所有通过“未匹配边→匹配边”交替路径可达的顶点， $S$ 由左集合未标记顶点和右集合标记顶点组成，可验证其为独立集且大小为 $N - M$ 。

基环树

基环树是“含恰好一个环的连通图”，分为无向基环树和有向基环树（环上所有边同向为单环树），核心处理思路是“拆环为树”。

找环：通过 DFS 或 BFS 找到环上的一条边 $e(u,v)$ ；
拆边转化为树：分别计算“不选边 $e$ ”（树的问题，如最大权路径、最大独立集）和“选边 $e$ ”（强制包含 $e$ ，处理两端子树）的结果；
合并结果：取两种情况的最优解。

例题

例题 1

link：A and B and Lecture Rooms。

给定一棵树，请回答 $m$ 次询问，每次给定两个点 $x,y$ ，求：
$\sum_{i=1}^{n} [\textrm{dis}(x,i)=\textrm{dis}(y,i)]$
其中 $\textrm{dis}(a,b)$ 表示树链 $a \to b$ 上点的个数。 $n,m \le 10^5$ 。

下文中，为了叙述方便，定义

\textrm{Jump}(i,j)

表示节点

i

往上跳

j

次所到达的结果（可以用

\log n

的倍增优化），

\textrm{size}_i

表示以

i

为根的子树的节点个数。

此题的关键在于如何快速求出

\textrm{dis}

的大小，并且实现时间复杂度小于

\mathcal{O}(n)

的查询处理方法。

考虑到两点距离

\textrm{dis}

可以被 LCA 优化，进行

\log n

的处理。但是即便是这样，

\mathcal{n \times m \times \log n}

也扛不住啊。

考虑到这两个点的中点（即链

a \to b

上满足条件的点 $）是题目的关键点，但题目的答案不止于中点。想到要从中点推广开一个式子。

尝试画一棵树搞一搞。

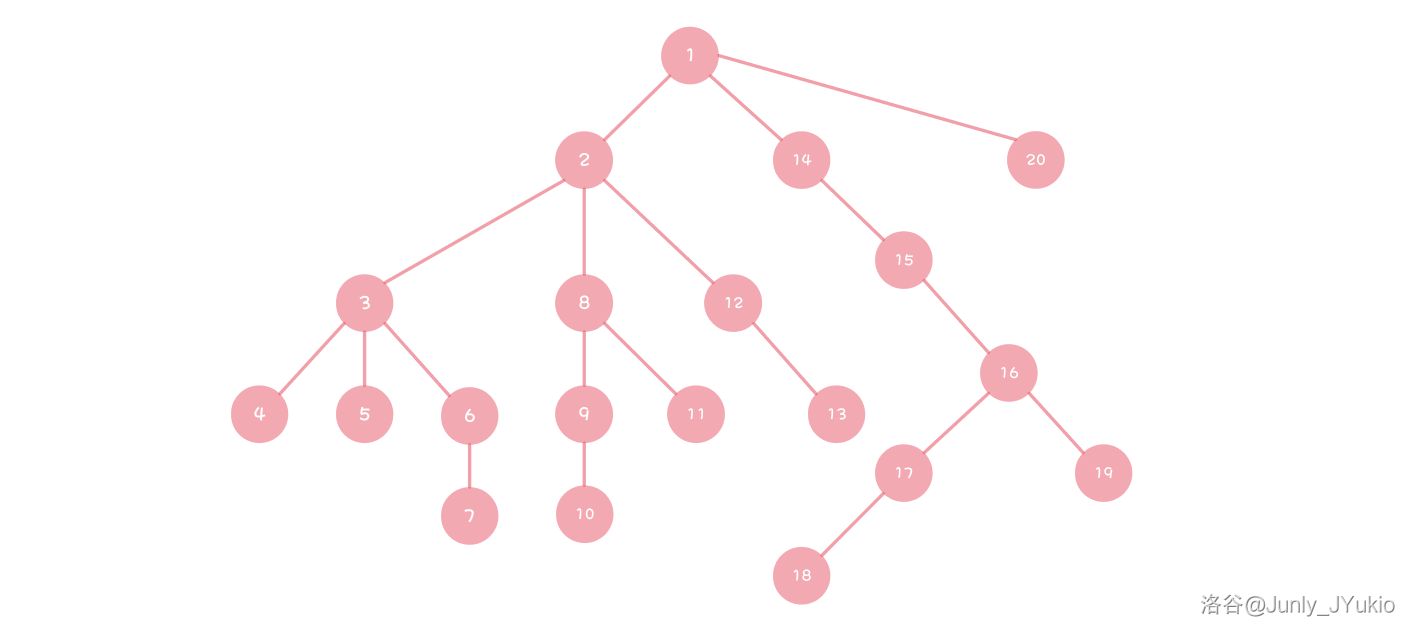
于是想到要使用分类讨论的做法来做，如下所示：

如果 $a=b$ ，那么所有点都满足 $\textrm{dis}(x,a)=\textrm{dis}(x,b)$ 。显然输出 $n$ 。
如果 $a \neq b$ $a \neq = b$ ，那么还需要额外判断这些点的中点在哪里。
- 如果这两点没有中点（即 $\textrm{dis}(a,b)\bmod 2 =0$ ），则可证两端和中间的点都不能满足条件，输出 $0$ 。
- 如果这两点存在中点，定义 $\textrm{len}= \frac{\textrm{dis}(a,b)-1}{2}$ 。还需要根据这两点的深度进行讨论。

那么应该怎样回答两点存在中点的情况呢？

如果 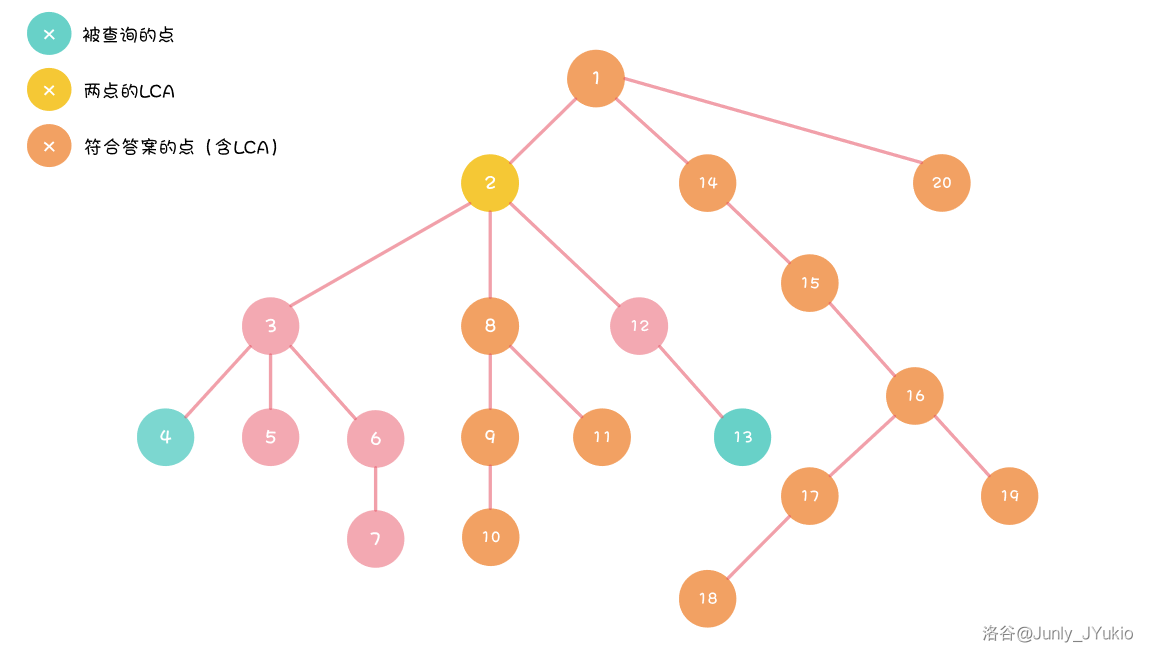$dep_a=dep_b$ 看上去答案好像出现在一个无法言说的子树上。发现答案好像就是不偏一边子树的节点数。则答案为：

n-\textrm{size}_{\textrm{Jump(a,\textrm{len-1})}}-\textrm{size}_{\textrm{Jump(b,\textrm{len-1})}}

可用

\mathcal{O}(\log n)

的时间复杂度处理。

如果 $dep_a \neq dep_b$

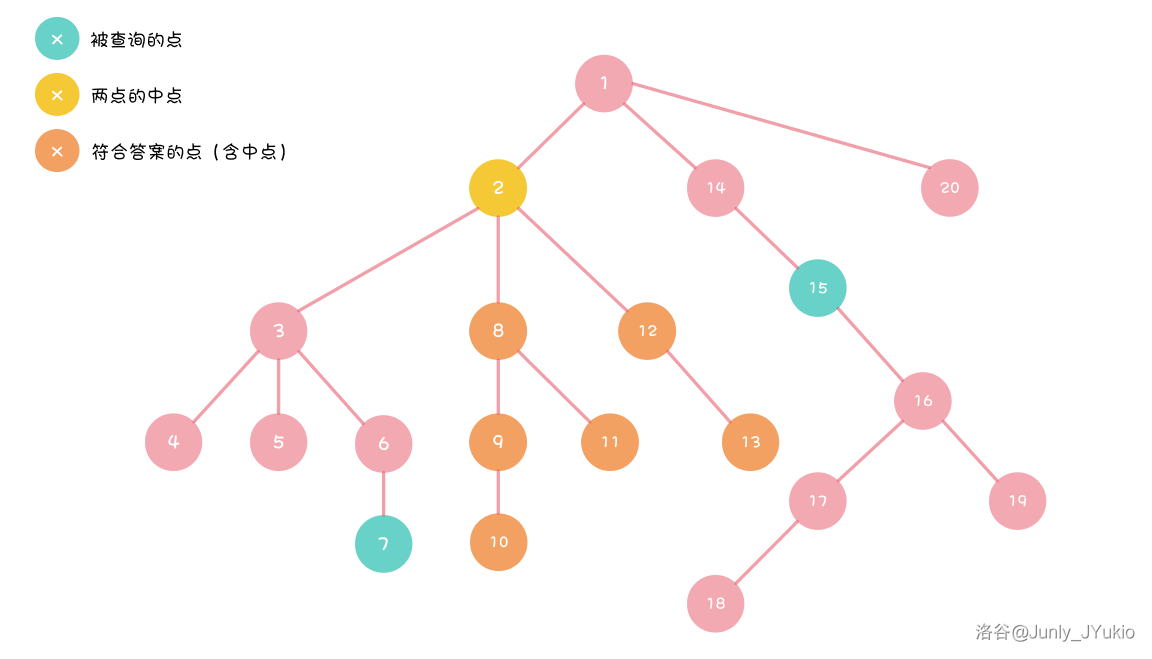
答案绝对是中点或者中点的子树。但是，答案中不能包含被查询的点一侧的子树。

定义

c

为

a

和

b

中深度较大的那个，故答案为：

\textrm{size}_{\textrm{Jump(c,\textrm{len})}}-\textrm{size}_{\textrm{Jump(c,\textrm{len-1})}}

仍然可用

\mathcal{O}(\log n)

的时间复杂度处理。

综上，此题可以使用

\mathcal{O}((n+m) \times \log n)

的时间复杂度完成。

代码

CPP

#include<cstdio>
#define N 100002
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
template<typename _Tp>
inline void read(_Tp& x) {
	x=0;
	while((ch=gc())<48);
	do x=(x<<3)+(x<<1)+(ch^48);
	while((ch=gc())>47);
}
template<typename _Tp>
inline void write(_Tp x) {
	if(x>9) write(x/10);
	putchar((x%10)^48);
}
int head[N],ver[N<<1],ne[N<<1],tot;
inline void add(int x,int y) {
	ver[++tot]=y;
	ne[tot]=head[x], head[x]=tot;
}
int n,fr,to,m,dep[N],f[N][20],flc,dist,sz[N];
inline void dfs(int x,int fa) {
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	sz[x]=1;
	for(int i=1; i<=19; i++) f[x][i]=f[f[x][i-1]][i-1];
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(fa==y) continue;
		dfs(y,x);
		sz[x]+=sz[y];
	}
}
inline int lca(int x,int y) {
	if(dep[x]<dep[y]) x^=y^=x^=y;
	for(int i=19; i>=0; i--) {
		if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	}
	if(x==y) return x;
	for(int i=19; i>=0; i--) {
		if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	}
	return f[x][0];
}
inline int Jump(int x,int step) {
	for(int i=19; i>=0; i--) {
		if((1<<i)&step) x=f[x][i];
	}
	return x;
}
int main() {
	read(n);
	for(int i=1; i<n; i++) {
		read(fr), read(to);
		add(fr,to);
		add(to,fr);
	}
	dfs(1,0);
	read(m);
	while(m--) {
		read(fr), read(to);
		if(fr==to) {
			write(n),putchar('\n');
			continue;
		}
		flc=lca(fr,to);
		dist=dep[fr]+dep[to]-dep[flc]-dep[f[flc][0]];
		if(!(dist&1)){
			write(0), putchar('\n');
			continue;
		}
		if(dep[fr]==dep[to]){
			write(n-sz[Jump(fr,dist/2-1)]-sz[Jump(to,dist/2-1)]), putchar('\n');
			continue;
		}
		if(dep[fr]>dep[to]) fr^=to^=fr^=to;
		write(sz[Jump(to,dist/2)]-sz[Jump(to,dist/2-1)]), putchar('\n');
	}
	return 0;
}

例题 2

link：疫情控制。

给定一棵树，根为 $1$ ，点编号 $1 \sim n$ ，带边权。令 $\textrm{dis}(i,j)$ 为树链 $i \to j$ 上的所有边权之和。

树上有 $m$ 枚棋子，第 $i$ 个棋子位于编号为 $c_i$ 的节点。你需要将这些棋子挪动到新位置，其中第 $i$ 个棋子移动至 $d_i(d_i \neq 1)$ ，使得在新的树中，从根节点到任意一个叶子节点的路径中，存在至少一枚棋子。

请输出： $\min(\max\limits_{i=1}^{m} \textrm{dis}(c_i,d_i))$ 。 $2 \le m \le n \le 5 \times 10^4$ ，边权 $0 < w < 10^9$ 。

注意到题目所要求的

\max\limits_{i=1}^{m} \textrm{dis}(c_i,d_i)

具有单调性：即对于某个方案，其花费为

t=\max\limits_{i=1}^{m} \textrm{dis}(c_i,d_i)

，则对于

\ge t

的每个方案，都一定可行，只需要在区间

[1,t-1]

去找寻答案了。

考虑二分

\textrm{now}=\max\limits_{i=1}^{m} \textrm{dis}(c_i,d_i)

。如何写出 check 呢？

尝试使用贪心。首先题意可以转化为：对于每个棋子，其能将以自己为根的子树染色。最后答案也就是需要将树中所有除根之外的点都染色。这样一来，就有如下性质：

对于每个棋子，如果其父亲不是根节点，且其剩余的 $\textrm{now}$ 能够支持其往上跳，就一定要跳至父亲。

证明很简单：其跳至父亲一定更优（能染色的节点更多），跳至子节点一定更劣（能染色的节点更少）。一个点只能跳至父亲、子节点，或原地不动，则如果能跳，就一定要跳。

但是这还不够。

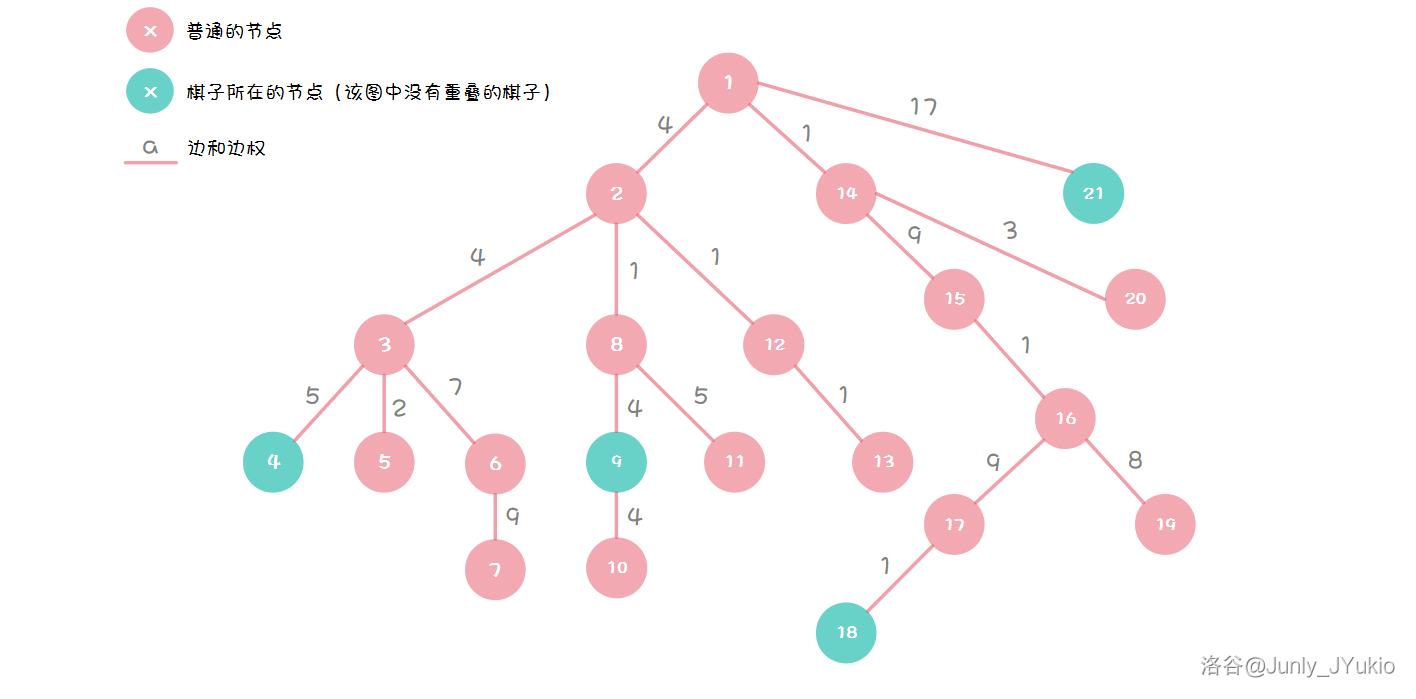
如图，如果只按照“一直往上跳，直到跳不动或者跳到根”的策略来进行，就会出现问题。

程序会这么看待几次操作：

棋子 A： $4 \to 3 \to 2$ ，需要花费： $9$ 。
棋子 B： $9 \to 8 \to 2$ ，需要花费： $5$ 。
棋子 C： $18 \to 17 \to 16 \to 15 \to 14$ ，需要花费： $20$ 。
棋子 D：原地不动。

此时需要花费的最大代价是

20

。

如果这么做呢：

棋子 A： $4 \to 3 \to 2$ ，需要花费： $9$ 。
棋子 B： $9 \to 8 \to 2 \to 1 \to 14$ ，需要花费： $10$ 。
棋子 C： $18 \to 17 \to 16$ ，需要花费： $10$ 。
棋子 D：原地不动。

此时需要花费的最大代价是

10

。

所以可见，一个棋子并不是移到根节点的儿子就一定停止。

因此，我们把所有走到根节点后代价仍

\le \textrm{now}

的棋子存下来，并且同时记录根节点有哪些叶子未被覆盖。

不妨把剩余可用路程更少的棋子分配给连接根节点与不合法的叶子的边的边权更小的孩子进行支援；若发现某个棋子无力支援分配给它的子树，那么这个棋子就留在自己的子树里。

此外，有余力支援其它部分的棋子，有留在自己子树的选择，此时代价为

0

。

综上所述，代码需要完成以下几个步骤：

预处理出所有点的深度，父亲和跳跃花费的代价；
二分值 $\textrm{now}$ $now$ ，check 写法如下：
- 使用类似于 LCA 的倍增法跳到自己力所能及的位置，如果能调到根节点的儿子就记录；
- 对于记录的棋子，不妨将根节点至所有儿子的边进行排序，而后又根据贪心思想，将所有可动棋子都移至根节点，并将这些点能走的剩余路径进行排序。显然，能走的最远的棋子应该去处理最远的儿子节点。

此题可 A。

代码

CPP

#include<cstdio>
#include<algorithm>
#define N 50002
#define int long long
using std::sort;
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
template<typename _Tp>
inline void read(_Tp& x) {
    x=0;
    while((ch=gc())<48);
    do x=(x<<3)+(x<<1)+(ch^48);
    while((ch=gc())>47);
}
int n,m,tot,fr,to,wi,l,r,mid,ans=-1,a[N],head[N],ver[N<<1],ne[N<<1],wei[N<<1],f[N][16],g[N][16];
bool vis[N];
struct data {
	int wei,id;
	bool operator < (const data &tool) const {
		return wei<tool.wei;
	}
} chess[N],bin[N];
inline void add(int x,int y,int w) {
	ver[++tot]=y,wei[tot]=w;
	ne[tot]=head[x],head[x]=tot;
}
inline void dfs(int x,int fa) {
	for(int j=1; j<=15; j++) {
		f[x][j]=f[f[x][j-1]][j-1];
		g[x][j]=g[x][j-1]+g[f[x][j-1]][j-1];
	}
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(y==fa) continue;
		f[y][0]=x;
		g[y][0]=wei[i];
		dfs(y,x);
	}
}
inline void putTag(int u,int fa) {
	bool res=1,flg=0;
	for(int i=head[u]; i; i=ne[i]) {
		int v=ver[i];
		if(v^fa) putTag(v,u),res&=vis[v],flg=1;
	}
	if(u!=1 and res and flg) vis[u]=1;
}
inline bool check(int lim) {
	for(int i=1; i<=n; i++) vis[i]=0;
	int flc=0,clf=0;
	for(int i=1; i<=m; i++) {
		int x=a[i],sum=0;
		for(int j=15; j>=0; j--) if(f[x][j]>1 and sum+g[x][j]<=lim) sum+=g[x][j],x=f[x][j];
		if(f[x][0]==1 and sum+g[x][0]<=lim) chess[++flc]=data {lim-sum-g[x][0],x};
		else vis[x]=1;
	}
	putTag(1,0);
	for(int i=head[1]; i; i=ne[i]) {
		int v=ver[i];
		if(!vis[v]) bin[++clf]=data {wei[i],v};
	}
	sort(chess+1,chess+flc+1);
	sort(bin+1,bin+clf+1);
	int pos=1;
	for(int i=1; i<=flc; i++) {
		if(!vis[chess[i].id]) vis[chess[i].id]=1;
		else if(chess[i].wei>=bin[pos].wei) vis[bin[pos].id]=1;
		while(vis[bin[pos].id] and pos<=clf) pos++;
	}
	return pos>clf;
}
signed main() {
	read(n);
	for(int i=1; i<n; i++) {
		read(fr), read(to), read(wi);
		add(fr,to,wi),add(to,fr,wi);
		r+=wi;
	}
	dfs(1,0);
	read(m);
	for(int i=1; i<=m; i++) read(a[i]);
	while(l<=r) {
		mid=(l+r)>>1;
		if(check(mid)) ans=mid,r=mid-1;
		else l=mid+1;
	}
	printf("%lld",ans);
	return 0;
}

例题 3

link：Max Flow P

有 $n$ 个节点的树， $q$ 次操作，每次将路径 $a \to b$ 上的所有点权加 $1$ ，求最终最大的点权。 $2 \le n \le 5 \times 10^4$ ， $1 \le q \le 10^5$ 。

学了前面的东西，这就是一道板中板题目。

预处理 LCA 的倍增数组和节点深度。
对每次操作，执行点差分修改。
后序遍历计算前缀和，还原每个节点的最终权值，记录最大值。

代码

CPP

#include<cstdio>
int s; 
char ch;
inline int read(){
    s=0;
    while((ch=getchar_unlocked())<48);
    do s=(s<<3)+(s<<1)+(ch^48);
    while((ch=getchar_unlocked())>47);
    return s;
}
int n,k,item,head[500002],ver[1000002],ne[1000002],tot,maxn,d[500002],dep[500002],f[500002][25],x,y;
inline void add(int x,int y) {
	ver[++tot]=y;
	ne[tot]=head[x],head[x]=tot;
}
inline void dfs(int x,int fa) {
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(int i=1; i<=20; i++) f[x][i]=f[f[x][i-1]][i-1];
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(y==fa) continue;
		dfs(y,x);
	}
}
inline int lca(int x,int y) {
	if(dep[x]<dep[y]) {item=x;x=y;y=item;}
	for(int i=20; i>=0; i--) {
		if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	}
	if(x==y) return x;
	for(int i=20; i>=0; i--) {
		if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	}
	return f[x][0];
}
inline void dfs2(int x,int fa) {
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(y==fa) continue;
		dfs2(y,x);
		d[x]+=d[y];
	}
	maxn=(maxn>d[x])?maxn:d[x];
}
int main() {
	n=read(), k=read();
	for(int i=1; i<n; i++) {
		x=read(), y=read();
		add(x,y), add(y,x);
	}
	dfs(1,0);
	while(k--) {
		x=read(), y=read();
		int p=lca(x,y);
		d[x]++,d[y]++;
		d[p]--,d[f[p][0]]--;
	}
	dfs2(1,0);
	printf("%d",maxn); 
	return 0;
}

例题 4

link：小 K 的农场。

有 $n$ 个农场，给你 $m$ 条约束信息，如下：

农场 $a$ 比农场 $b$ 至少多种植了 $c$ 个单位的作物；

农场 $a$ 比农场 $b$ 至多多种植了 $c$ 个单位的作物；

农场 $a$ 与农场 $b$ 种植的作物数一样多。

问是否存在合法的农场作物分配满足所有约束条件。

简单差分约束题。其中，“至少多”和“至多多”明显可以直接用建边法来做；

农场

a

比农场

b

至少多种植了

c

个单位的作物代表

a-b \ge c

，可以表示为

b \to a

，权值为

-c

。

而农场

a

比农场

b

至少多种植了

c

个单位的作物代表

a-b \le c

，可以表示为

a \to b

，权值为

c

。

至于“相等”，则可以建一条双向边，两条权值均为

0

，因为若

a \le b

，

b \le a

，则

a=b

。在判断负环后，输出 No(有负环) 或者 Yes(没负环) 即可。

此题可解。

代码

CPP

#include<bits/stdc++.h>
#define F first
#define S second
#define PII pair<int,int>
using namespace std;
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
int f;
template<typename _Tp>
inline void read(_Tp& x) {
	x=0, f=1;
	do if(ch=='-') f=-1;
	while((ch=gc())<48);
	do x=(x<<3)+(x<<1)+(ch^48);
	while((ch=gc())>47);
	x*=f;
}
template<typename _Tp>
inline void write(_Tp x) {
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar((x%10)^48);
}
vector<PII> vec[5002];
int n,m,fr,to,wi,dis[5002],op;
bool bell;
int main() {
	read(n), read(m);
	for(int i=1; i<=m; i++) {
        read(op);
        if(op==1){
            read(fr), read(to), read(wi);
        	vec[to].push_back({fr,-wi});
        }else if(op==2){
            read(fr), read(to), read(wi);
        	vec[fr].push_back({to,wi});
        }else{
            read(fr), read(to);
            vec[to].push_back({fr,0});
            vec[fr].push_back({to,0});
        }
	}
	for(int i=1; i<=n; i++) vec[0].push_back({i,0}),dis[i]=2e9;
	dis[0]=0;
	for(int i=1; i<=n; i++) {
		bell=0;
		for(int j=0; j<=n; j++) {
			if(dis[j]==2e9) continue;
			for(PII k:vec[j]) if(dis[k.F]>dis[j]+k.S) {
					dis[k.F]=dis[j]+k.S;
					bell=1;
				}
		}
		if(!bell) break;
	}
	bell=0;
	for(int j=1; j<=n; j++) {
		if(dis[j]==2e9) continue;
		for(PII k:vec[j]) if(dis[k.F]>dis[j]+k.S) {
				dis[k.F]=dis[j]+k.S;
				bell=1;
			}
		if(bell) break;
	}
	if(bell){
		puts("No");
		return 0;
	}
    puts("Yes");
	return 0;
}

练习题

例题 5

link：Grass Cownoisseur G。

考虑分层图。在缩点后，对于“只逆行一次”的处理方案可以设两层图，第一层图和第二层图之间靠反边连结。此题可解。

代码

CPP

#include<cstdio>
#include<vector>
#include<queue>
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
int s;
inline int read(){
    s=0;
    while((ch=gc())<48);
    do s=(s<<3)+(s<<1)+(ch^48);
    while((ch=gc())>47);
    return s;
}
std::vector<int> vec[300002];
int n,m,head[100002],ver[100002],ne[100002],tot,fr,to,fx,fy,dist[200002];
inline void add(int x){
	ver[++tot]=read();
    ne[tot]=head[x], head[x]=tot;
} 
int dfn[100002],low[100002],st[100002],top,num,z,cnt,scc[100002],sz[200002],tag[200002];
bool vis[100002];
void tarjan(int x){
	dfn[x]=low[x]=++num;
	vis[x]=1,st[++top]=x;
	for(int i=head[x]; i; i=ne[i]){
		int y=ver[i];
		if(!dfn[y]){
			tarjan(y);
			if(low[y]<low[x]) low[x]=low[y];
		}else if(vis[y] and dfn[y]<low[x]) low[x]=dfn[y];
	}
	if(dfn[x]==low[x]){ // 当前点 x 是一个新的堆的开头 
		cnt++;
		while(true){
			z=st[top--];
			scc[z]=cnt;
			sz[cnt]++;
			vis[z]=0;
			if(x==z) break;
		}
	}
} 
int main(){
	n=read(), m=read();
	for(int i=1; i<=m; i++) add(read());
	for(int i=1; i<=n; i++) if(!dfn[i]) tarjan(i);
	if(cnt==1){
		printf("%d",n);
		return 0;
	}
	// 构建第二层图结构 
	for(int x=1; x<=n; x++){
		fx=scc[x];
		for(int i=head[x]; i; i=ne[i]){
			fy=scc[ver[i]];
			if(fx==fy) continue;
			// 警示后人:是 cnt 不是 n 
			vec[fx].push_back(fy); // 正常建边
			vec[fy].push_back(fx+cnt); // 在第二层和第一层里建边
			vec[fx+cnt].push_back(fy+cnt); // 在第二层开建 
		}
	}
	for(int i=1; i<=cnt; i++) sz[i+cnt]=sz[i]; // 复制权值 
	// 使用 SPFA 跑最短路 
	std::queue<int> qu;
	qu.push(scc[1]); // 警示后人：是 scc[1] 不是 1 
	tag[scc[1]]=1;
	while(!qu.empty()){
		int x=qu.front();
		qu.pop();
        tag[x]=0;
		for(int i=0; i<vec[x].size(); i++){
			int y=vec[x][i];
			if(dist[y]<dist[x]+sz[y]){
				dist[y]=dist[x]+sz[y];
				if(!tag[y]){
					tag[y]=1;
					qu.push(y);
				}
			}
		}
	}
	printf("%d",dist[scc[1]+cnt]);
	return 0;
}

例题 6

link：Knights Of The Round Table。

首先，我们知道点双连通分量由一堆环组成。

假设在点双连通分量之中有环

a

，若

a

是奇环，那么

a

中所有点都可以开会，不影响答案。

若

a

是偶环，那么将它和点双中的奇环链接成一个大奇环就可以了。

诶，那这简单了。

先建补图，补图上 Tarjan 求点双，对于每一个点双二分图染色判断是否有奇环，不在任何一个有奇环的点双上的点都无法参加会议。

此题可解。

代码

CPP

#include<cstdio>
int s;
char ch;
inline int read(){
    s=0;
    while((ch=getchar())<48);
    do s=(s<<3)+(s<<1)+(ch^48);
    while((ch=getchar())>47);
    return s;
}
inline void write(int x){
    if(x>9) write(x/10);
    putchar(x%10+48);
}
int head[1002],ver[2000005],ne[2000005],tot;
inline void add(int x,int y){
	ver[++tot]=y;
	ne[tot]=head[x],head[x]=tot;
}
int n,m,p[1002][1002],fr,to;
inline void solve(){
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++) p[i][j]=0;
	}
	m=read();
	for(int i=1; i<=m; i++){
		fr=read(), to=read();
		p[fr][to]=p[fr][to]=1;
	}
	for(int i=1; i<=n; i++){
		for(int j=i+1; j<=n; j++) if(!p[i][j]) add(i,j),add(j,i);
	}
	for(int i=1; i<=n; i++){
		if(!dfn[i]){
			
		}
	}
}
int main(){
	while(n=read()) solve();
	return 0;
}

例题 7

link：银河。

差分约束。但是此题还需要求最小值。

考虑 SCC 缩点法。在缩点之后，所有可以相等的值成为一个强连通分量。再在小图上作拓扑排序，此题可解。

代码

CPP

#include<cstdio>
#include<vector>
#include<queue>
int s;
char ch;
inline int read() {
	s=0;
	while((ch=getchar())<48);
	do s=(s<<3)+(s<<1)+(ch^48);
	while((ch=getchar())>47);
	return s;
}
int head[100002],ne[200002],ver[200002],w[200002],tot;
inline void add(int x,int y,int z) {
	ver[++tot]=y, w[tot]=z;
	ne[tot]=head[x], head[x]=tot;
}
int n,m,t,a,b,du[100002],dfn[100002],low[100002],st[100002],scc[100002],sz[100002],dis[100002],top,num,cnt,z,fx;
long long ans;
bool vis[100002];
std::vector<int> vec[100002],wec[100002];
inline void tarjan(int x) {
	dfn[x]=low[x]=++num;
	st[++top]=x, vis[x]=1;
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(!dfn[y]) {
			tarjan(y);
			if(low[y]<low[x]) low[x]=low[y];
		} else if(vis[y] and dfn[y]<low[x]) low[x]=dfn[y];
	}
	if(low[x]==dfn[x]) {
		cnt++;
		while(true) {
			z=st[top--];
			scc[z]=cnt;
			vis[z]=0;
			sz[cnt]++;
			if(x==z) break;
		}
	}
}
int main() {
	n=read(), m=read();
	for(int i=1; i<=m; i++){
		t=read(), a=read(), b=read();
		if(t==1) add(a,b,0),add(b,a,0);
		else if(t==2) add(a,b,1);
		else if(t==3) add(b,a,0);
		else if(t==4) add(b,a,1);
		else if(t==5) add(a,b,0);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i])
			tarjan(i);
	}
	bool flag=0;
	for(int x=1; x<=n; x++){
		for(int i=head[x]; i; i=ne[i]){
			int y=ver[i];
			if(scc[x]==scc[y]){
				if(w[i]>0){
					puts("-1");
					return 0;
				}
				continue;
			}
			vec[scc[x]].push_back(scc[y]);
			wec[scc[x]].push_back(w[i]);
			du[scc[y]]++;
		}
	}
	
	std::queue<int> q;
	for(int i=1; i<=cnt; i++) {
		if(du[i]==0) {
			q.push(i);
			dis[i]=1;
		}
	}
	while(!q.empty()) {
		int x=q.front();
		q.pop();
		for(int i=0; i<vec[x].size(); i++) {
			int y=vec[x][i];
			du[y]--;
			if(dis[y]<dis[x]+wec[x][i]) dis[y]=dis[x]+wec[x][i];
			if(du[y]==0) q.push(y);
		}
	}
	for(int i=1; i<=cnt; i++) ans+=(long long)sz[i]*dis[i];
	printf("%lld",ans);
	return 0;
}

例题 8

link：游戏。

乍眼一看，此题好像是一个 3-SAT 问题，因为在特殊赛道 x 上，存在

3

种属性值，不再是布尔变量。这样一来，貌似此题就成为了 NP-难问题。

一种暴力的想法是枚举 x 地图不用哪一种车，将 x 地图转化为一般地图求解。这样状态总数将达到

3^d

，明显无法承受。

注意到上面的枚举过程中，我们没有必要枚举所有三种普通地图，只用枚举两种地图即可。因为任意两种普通地图的组合，都能完整覆盖三种可用的车。在

\mathcal{\omega}(2^d)

的复杂度内，此题可解。

代码

CPP

#include<cstdio>
#include<string>
#define For(i,a,b) for(int i=a; i<=b; i++)
#define N 150002
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXSIZE,stdin),p1==p2)?EOF:*p1++)
constexpr int MAXSIZE=2e5;
char buf[MAXSIZE],*p1,*p2;
inline char getc() {
	char c=gc();
	while(c>'Z' or c<'A')c=gc();
	return c;
}
inline std::string READ() {
	std::string ret="";
	char c=gc();
	while(c==' ' or c=='\n') c=gc();
	while(c!=' ' and c!='\n') ret+=c,c=gc();
	return ret;
}
inline int read() {
	int ans=0;
	char c=gc();
	while(c>'9' or c<'0') c=gc();
	while(c>='0' and c<='9') ans=(ans<<1)+(ans<<3)+(c^48),c=gc();
	return ans;
}
struct node {
	int a,x,b,y;
} a[N];
int head[N],ver[N],ne[N],tot;
inline void add(int x,int y) {
	ver[++tot]=y;
	ne[tot]=head[x], head[x]=tot;
}
std::string str;
char op;
int n,m,d,s[N][2],plc[N],cur,dfn[N],low[N],st[N],scc[N],top,z,num,cnt,h1,h2;
bool flag;
inline void tarjan(int x) {
	dfn[x]=low[x]=++num,st[++top]=x;
	for(int i=head[x]; i; i=ne[i]) {
		int y=ver[i];
		if(!dfn[y]) {
			tarjan(y);
			if(low[y]<low[x]) low[x]=low[y];
		} else if(!scc[y] and dfn[y]<low[x]) low[x]=dfn[y];
	}
	if(low[x]==dfn[x]) {
		cnt++;
		while(true) {
			z=st[top--];
			scc[z]=cnt;
			if(z==x) break;
		}
	}
}
int main() {
	n=read(), d=read();
	str=READ();
	m=read();
	For(i,1,n) {
		op=str[i-1];
		if(op=='a') s[i][0]=2,s[i][1]=3;
		else if(op=='b') s[i][0]=1,s[i][1]=3;
		else if(op=='c') s[i][0]=1,s[i][1]=2;
		else plc[++cur]=i;
	}
	For(i,1,m) a[i]= {read(),getc()-'A'+1,read(),getc()-'A'+1}; //?
	For(i,0,(1<<cur)-1) {
		tot=num=cnt=top=0;
		flag=0;
		For(j,0,n<<1) low[j]=dfn[j]=scc[j]=head[j]=0;
		For(j,1,cur) s[plc[j]][0]=1,s[plc[j]][1]=((1<<(j-1))&i)?2:3;
		For(j,1,m) {
			int h1=-1,h2=-1;
			if(s[a[j].a][0]==a[j].x) h1=0;
			else if(s[a[j].a][1]==a[j].x) h1=1;
			if(s[a[j].b][0]==a[j].y) h2=0;
			else if(s[a[j].b][1]==a[j].y) h2=1;
			if(h1==-1) continue;
			if(h2==-1) add(a[j].a+h1*n,a[j].a+(h1^1)*n);
			else add(a[j].a+h1*n,a[j].b+h2*n),add(a[j].b+(h2^1)*n,a[j].a+(h1^1)*n);
		}
		For(j,1,n<<1)if(!dfn[j]) tarjan(j);
		For(j,1,n) if(scc[j]==scc[n+j]) {
			flag=1;
			break;
		}
		if(flag) continue;
		For(j,1,n) putchar(s[j][scc[j]>scc[n+j]]+'A'-1);
		return 0;
	}
	puts("-1");
	return 0;
}

// 一个很妙的点：x 可以成为 a,b 的结合体，这样就能通过所有的车；将 3-SAT 问题通过一次暴力搜索变为 2-SAT 问题。

例题 9

link：连续攻击游戏。

一个装备只能提供一个属性。

二分图匹配当中，一个点只能和一个点匹配。

我们把两个属性值当做两个点来连线。

此题可解。

代码

CPP

#include<bits/stdc++.h>
using namespace std;

const int N=1e6+5;
vector<int> belong[N];
int a[N],b[N],cnt[N];
int num,ans,vis[N];

inline void dfs(int step){
    num++;
    ans=max(ans,step);
    if(num==2e7){
        cout<<ans;
        exit(0);
    }
    for(int i=0;i<belong[step+1].size();i++){
        int y=belong[step+1][i];
        if(vis[y]) continue;//去过了
        vis[y]=1;
        dfs(step+1);
        vis[y]=0;
    }
}

int main(){
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        scanf("%d %d",&a[i],&b[i]);
        cnt[a[i]]++,cnt[b[i]]++;
        belong[a[i]].push_back(i);
        belong[b[i]].push_back(i);
    }
    for(int i=1;i<=n;i++){
        if(cnt[a[i]]>=cnt[b[i]]) cnt[a[i]]--;
        else cnt[b[i]]--;
    }
    for(int i=1;;i++){
        if(cnt[i]==0) break;
        ans++;
    }
    dfs(0);
    cout<<ans;
	return 0;
}

文章操作

省流：LCA，树上差分，重链剖分，差分约束，tarjan，2 - SAT，二分图基础，基环树。

放在前面

最近公共祖先、树上前缀和、树上差分

Ⅰ. 最近公共祖先

Ⅱ. 最近公共祖先所具有的性质

Ⅲ. 树上差分

1. 点差分（节点路径修改）

核心修改规则

结果还原（后序遍历前缀和）

2. 边差分（边路径修改）

核心修改规则

结果还原（后序遍历前缀和）

应用场景

Ⅳ. 三者关联与核心思想

重链剖分

Ⅰ. 重链剖分基础

Ⅱ. 重链剖分的应用

1. 求最近公共祖先（LCA）

2. 路径信息维护

3. 子树信息维护

差分约束

Tarjan 算法

Ⅰ. dfn\textrm{dfn}dfn 序和 low\textrm{low}low 数组

Ⅱ. 强连通分量（SCC）

核心原理

核心实现代码

应用场景

Ⅲ. 边双连通分量（E - DCC）

核心原理

板子代码

Ⅳ. 点双连通分量（V - DCC）

核心原理

核心实现代码

2 - SAT 适应性问题

Ⅰ. 核心建模

1. 变量与节点映射

2. 约束转化逻辑推导

Ⅱ. 可行性判定与求解逻辑

1. 可行性判定原理

2. 可行解构造逻辑

二分图基础

Ⅰ. 二分图的定义与判定

定义

判定算法（染色法）

核心实现代码

Ⅱ. 二分图最大匹配

1. 匹配相关定义

2. 匈牙利算法（求最大匹配）

（1）算法步骤（以 UUU 为左集合，VVV 为右集合为例）

匈牙利算法

实现代码

Ⅲ. 二分图最大独立集与最小点覆盖

1. 核心定义

2. Konig 定理（二分图特有）

基环树

例题

例题 1

例题 2

例题 3

例题 4

练习题

例题 5

例题 6

例题 7

例题 8

例题 9

相关推荐

评论

Ⅰ. $\textrm{dfn}$ 序和 $\textrm{low}$ 数组

（1）算法步骤（以 $U$ 为左集合， $V$ 为右集合为例）