专栏文章

基础数据结构重拾：再谈栈、队列与链表

JJunly_JYukio
算法·理论参与者 4已保存评论 6

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
6 条
当前快照
1 份
快照标识符
@mk49n9iq
此快照首次捕获于
2026/01/08 01:02
上个月
此快照最后确认于
2026/02/19 01:21
17 小时前
查看原文

放在最前面

本文由 MoonCake2011 和 Junly_JYukio 联合制作。
题单链接：link。
大多数例题：MoonCake2011。
摸鱼：Junly_JYukio。
防伪验证：下文 lg⁡\lg 一律不表示 log⁡2\log_2。
MoonCake 的前言：嗯嗯嗯嗯嗯嗯嗯嗯嗯嗯嗯嗯我喜欢摸一个蓝色的鱼。
大多数代码由 MoonCake2011 编写，部分代码来自 Junly_JYukio。

放在前面

本文并非“应用基础数据结构教程”，只用于快速记忆栈、队列、链表一类基础数据结构的有趣应用。
数据结构在信息学竞赛中处处可见，可以说“程序离不开数据结构”。变量、数组、hash 表、线段树等，都是数据结构。我之前在一篇文章中已经提到过各类进阶的数据结构，不过本文相对简单，仅仅谈论栈、队列与链表这三个非常基础的线性数据结构。
本文也不适合身经百战的大佬。诶，那本文适合谁啊。
本文将总结比较简单的常见基础数据结构的应用，希望各位能透过本文，重新审视这些有趣问题。

栈

1.1 基本思想回顾

栈，或 LIFO 表，是一种先进后出的线性数据结构，应用栈的算法一般来说都会非常频繁地访问栈顶，即当前最后进入，也是接下来最先弹出的元素。
栈的实现方式也有许多，对我来说最常见的当然是一个线性数组 + 一个指针来实现。
序列实现栈CPP
int st[N],top; // top 表示当前栈顶的下标，这里的 st 是 1-based 序列
inline void ins(int x){ // 在栈中插入元素 x
  st[++top]=x;
}
inline int del(){ // 删除并返回栈顶
  return st[top--];
}
inline void clear(){ // 将栈清空
  top=0;
}
系统自带的 std::stack 实现栈CPP
std::stack<int> st; // 定义存储普通整形变量的栈
st.push(1); // 在栈顶插入 1
st.top(); // 返回当前栈顶
st.pop(); // 弹出栈顶
st.empty(); // 返回是否为空
st.size(); // 返回元素数量

例题 1

板子题。
请你实现一个栈，支持如下操作：
  • push(x)：向栈中加入一个数 xx。
  • pop()：将栈顶弹出。如果此时栈为空则不进行弹出操作，输出 Empty。
  • query()：输出栈顶元素，如果此时栈为空则输出 Anguei!。
  • size()：输出此时栈内元素个数。
显然，所有操作直接在序列上模拟即可；栈内当前元素个数可以直接用 top 表示。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n,top;
unsigned long long stk[10000002];
string req;
inline void solve(){
    cin>>n;
    top=0;
    while(n--){
        cin>>req;
        if(req[2]=='s'){ // push
            ++top;
            cin>>stk[top];
        }else if(req[2]=='p'){ // pop
            if(top==0) cout<<"Empty\n";
            else --top;
        }else if(req[2]=='e'){ // query
            if(top==0) cout<<"Anguei!\n";
            else cout<<stk[top]<<"\n";
        }else{ // size
            cout<<top<<"\n";
        }
    }
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int T;
    cin>>T;
    while(T--) solve();
    return 0;
}

1.2 栈的简单应用

由于栈本身 LIFO 的特性天生适合部分问题，所以在这类问题上，对栈的使用较多。
比如：
  • 将中缀表达式转为后缀表达式，或计算一个后缀表达式的值。
  • 判断一个括号序列是否合法。
  • 深度优先搜索的顺序。
遇到这类问题应当就题解题，灵活使用栈的思想。

例题 2

栈。
设 nn 个数的答案为 fnf_n。
尝试枚举最后一个出栈的元素 kk。
比 kk 之前入栈的绝对在 kk 进栈前就全部出去了，方案数为 fk−1f_{k-1}。
在 kk 后面的数也可以形成一个出栈序列，方案数 fn−kf_{n-k}。
初值为 f0=f1=1f_0=f_1=1，递推即可。
代码CPP
#include <iostream>
int n,f[25];
int main() {
    scanf("%d",&n);
	f[0]=1;
	for(int i=1; i<=n; i++) for(int j=0; j<i; j++) f[i]+=f[j]*f[i-j-1];
    printf("%d",f[n]);
	return 0;
}

例题 3

时间复杂度。
此题需要模拟循环语句。
我们发现循环语句满足后开始的循环语句必须先出去，所以可以用栈模拟。
这也有一个栈的关键性质（也可以说成定义）：先进先出。
有时候，我们可以用栈模拟递归来减少常数。
代码CPP
#include<bits/stdc++.h>
using namespace std;
inline int read(){
	char ch=getchar();int x=0;
	while(!isdigit(ch) && ch!='n') ch=getchar();
	if(ch=='n') return 65535;
	while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
} 
bool p[11110];
void solve(){
	memset(p,0,sizeof p);
	int l,bs;
	char FW;
	cin>>l>>FW;
	cin>>FW;cin>>FW;
	if(FW=='1') bs=0;
	else cin>>FW>>bs;
	cin>>FW;
//	getchar();//吃个换行 
	int cnt=0,BS=0,nbs=0; 
	stack<int>op,run,CH;
	bool err=0,norun=0;
	for(int i=1;i<=l;i++){
		char ch;
		cin>>ch;
		if(ch=='F'){
			char nm;
			cin>>nm;
			if(p[nm]) err=1;
			p[nm]=1,CH.push(nm); 
			cnt++;
			int x=read(),y=read();
			if(y-x>100) nbs++,op.push(1),run.push(norun);
			else if(y-x<0) op.push(0),norun=1,run.push(norun);
			else op.push(0),run.push(norun);
		}
		else{
			cnt--;
			if(cnt<0) err=1;
			if(err) continue;
			nbs-=op.top(),op.pop(),run.pop();
			if(!run.empty()) norun=run.top();else norun=0;
			p[CH.top()]=0,CH.pop();
		}
		if(!norun) BS=max(BS,nbs);
	}
	if(cnt!=0) err=1;
	if(err) cout<<"ERR\n";
	else if(bs==BS) cout<<"Yes\n";
	else cout<<"No\n";
}
int main() {
	int t;
	cin>>t;
	while(t--) solve();
	return 0;
}

例题 4

验证栈序列。
考虑模拟过程，因为出栈序列是依次出栈的，所以我们可以尝试将入栈序列依次推进栈里，如果此时栈顶为出栈序列的第一个数，那我们就将它出栈，接着我们要找第二个数。
也同理，如果栈顶是第二个数，就将第二个数出栈。
剩下的数依次。
可以证明一个数能出栈尽量提早出栈，可能防止它影响后面的数。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n,q;
stack<int>s;
int main() {
	cin>>q;
	for(int i=1;i<=q;i++){
		cin>>n;
		const int a=n;
		int pu[a+10],po[a+10];
		int sum=1;
		for(int i=1;i<=n;i++) cin>>pu[i];
		for(int i=1;i<=n;i++) cin>>po[i];
		for(int i=1;i<=n;i++){
			s.push(pu[i]);
			while(s.top()==po[sum]){
				s.pop();
				sum++;
				if(s.empty())
					break;
			}
		}
		if(s.empty())
			cout<<"Yes\n";
		else{
			cout<<"No\n";
			while(!s.empty()) s.pop();
		}
	}
	return 0;
}

例题 5

双栈排序。
先考虑验证。
如果是单栈的话，我们可以像上道题一样直接模拟来判断。
对于双栈，这样做肯定是不行了，可以发掘其中的性质。
考虑数的出栈顺序，如果 pi<pjp_i<p_j，ii 就要在 jj 之前出栈。
如果一个数 kk 满足 i<j<ki<j<k 且 pk<pi<pjp_k<p_i<p_j，那么 kk 比 ii 和 jj 都先出栈，此时如果要出栈的话，那么 ii 需要在 jj 后面出栈，不满足。
对于这样 ii 和 jj 是不能共存的。
于是考虑对于点分配到两个栈里，可以建立二分图的模型，将这样的 ii 和 jj 连边，表示不能分配到同一个栈里。
跑二分图染色即可判断是否有解。
接着像上一道题模拟就行了吗？
不行，因为要要求字典序最小。
我们发现，有时候第二个栈的入栈操作可以放到第一个栈的出栈操作之后，因为两个操作互不影响。
第二个栈的出栈操作也可以放到第一个栈的入栈操作之后。
像这样冒泡排序一下就可以求出答案了。
这道题思维难度感觉挺高的。
Junly 的实现CPP
#include<cstdio>
#define N 1002
char ch;
inline char gc() {
	static char buf[1<<18],*p1=buf,*p2=buf;
	if(p1==p2) {
		p2=(p1=buf)+fread(buf,1,1<<18,stdin);
		if(p1==p2) return EOF;
	}
	return *p1++;
}
template<typename _Tp>
inline void read(_Tp& x) {
	x=0;
	while((ch=gc())<48);
	do x=(x<<3)+(x<<1)+(ch^48);
	while((ch=gc())>47);
}
template<typename _Tp>
inline void write(_Tp x) {
	if(x>9) write(x/10);
	putchar((x%10)^48);
}
int head[N],ver[N*N],nex[N*N],tot;
inline void add(int x,int y) {
	ver[++tot]=y;
	nex[tot]=head[x], head[x]=tot;
}
bool flag=0,mymy=0;
int n,arr[N],col[N],minn[N];
inline void dfs(int x) {
	if(flag) return;
	for(int i=head[x]; i; i=nex[i]) {
		int y=ver[i];
		if(col[y]) {
			if(col[y]+col[x]!=3) {
				flag=1;
				return;
			}
			continue;
		}
		col[y]=3-col[x];
		dfs(y);
	}
}
int sta[N],stb[N],topa,topb,c_cnt,buc[N<<2];
char c[N<<2];
inline void ins(char pos){
	if(pos!=c[c_cnt]) c[++c_cnt]=pos;
	++buc[c_cnt];
}
inline void pushina(int val){
	while(topa and val>sta[topa]){
		while(topb and stb[topb]<sta[topa]){
			--topb;
			ins('d');
		}
		--topa;
		ins('b');
	}
	sta[++topa]=val;
	ins('a');
}
inline void pushinb(int val){
	while(topb and val>stb[topb]){
		while(topa and sta[topa]<stb[topb]){
			--topa;
			ins('b');
		}
		--topb;
		ins('d');
	}
	stb[++topb]=val;
	ins('c');
}
inline void totally_pop(){
	while(topa and topb){
		if(sta[topa]>stb[topb]){
			--topb;
			ins('d');
		}else{
			--topa;
			ins('b');
		}
	}
}
inline void extra_popa(){
	while(topa){
		--topa;
		ins('b');
	}
}
inline void extra_popb(){
	while(topb){
		--topb;
		ins('d');
	}
}
inline void sorty(){
	for(int i=1; i<c_cnt; i++){
		if(c[i]=='c' and c[i+1]=='b'){
			c[i]='b';
			c[i+1]='c';
			buc[i]^=buc[i+1]^=buc[i]^=buc[i+1];
		}
		if(c[i]=='d' and c[i+1]=='a'){
			c[i]='a';
			c[i+1]='d';
			buc[i]^=buc[i+1]^=buc[i]^=buc[i+1];
		}
	}
}
int main() {
	read(n);
	for(int i=1; i<=n; i++) read(arr[i]);
	minn[n]=arr[n];
	for(int i=n-1; i>=1; i--) minn[i]=minn[i+1]>arr[i]?arr[i]:minn[i+1];
	for(int i=1; i<=n; i++)
		for(int j=i+1; j<n; j++)
			if(arr[i]<arr[j] and minn[j+1]<arr[i]) add(i,j),add(j,i);

	for(int i=1; i<=n; i++) if(!col[i]) col[i]=1,dfs(i);
	if(flag) putchar(48);
	else {
		// 如果颜色不同，必分居两栈之侧；否则，可进同一栈。
		// 注意：其中一栈必该进就近，该出就出；另一栈，尽量晚出为好。
		if(col[1]==2) for(int i=1; i<=n; i++) col[i]=3-col[i]; 
		for(int i=1; i<=n; i++) col[i]&1?pushina(arr[i]):pushinb(arr[i]);
		totally_pop(); extra_popa(); extra_popb(); sorty();
		for(int i=1; i<=c_cnt; i++) while(buc[i]--) putchar(c[i]),putchar(32); 
	}
	return 0;
}

/*
昨天晚上就在入栈和出栈序列上面卡了很久，今天重新挑战。
每个元素，都要经历入栈和出栈。在每个元素的归属之栈确定的情况下，a 与 b 的顺序不可能颠倒，c 与 d 亦然。所以，问题就出在前栈和后栈交接的地方。
既然如此，就会遇到很多窘境，我不禁想到：当遇到这样的操作序列时：

ccbb 这种情况应该直接改成 bbcc，显然。 
ddaa 这种情况应该直接改成 aadd，显然。
还有吗。诶好像没了。
做完了(1/1)。 
*/
Mooncake 的实现CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[1010],mn[1010];
vector<int>e[1010];
int col[1010];
bool flag=1;
inline void dfs(int x){
	int c=3-col[x];
	for(int i=0;i<e[x].size();i++)
		if(col[e[x][i]]) if(col[e[x][i]]!=c) flag=0;else;
		else col[e[x][i]]=c,dfs(e[x][i]);
}
stack<int>st[2];
vector<char>opt;
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	mn[n+1]=n+1;
	for(int i=n;i>=1;i--) mn[i]=min(mn[i+1],a[i]);
	for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(mn[j+1]<a[i] && a[i]<a[j]) e[i].push_back(j),e[j].push_back(i);
	for(int i=1;i<=n;i++) if(!col[i]) col[i]=1,dfs(i);
	if(!flag){
		cout<<0;
		return 0;
	}
	int k=0;
	for(int i=1;i<=n;i++){
		col[i]--;
		st[col[i]].push(a[i]),opt.push_back(col[i] ? 'c' : 'a');
		while((!st[0].empty() && st[0].top()==k+1) || (!st[1].empty() && st[1].top()==k+1)){
			if(!st[0].empty() && st[0].top()==k+1) k++,st[0].pop(),opt.push_back('b');
			if(!st[1].empty() && st[1].top()==k+1) k++,st[1].pop(),opt.push_back('d');
		}
	}
	for(int i=0;i<2*n;i++)
		for(int j=i+1;j<2*n;j++) if((opt[j-1]=='c' && opt[j]=='b') || (opt[j-1]=='d' && opt[j]=='a')) swap(opt[j-1],opt[j]);
	for(int i=0;i<2*n;i++) cout<<opt[i]<<" ";
	return 0;
}

1.3 单调栈

例题 6

单调栈。
考虑排除没有用的选项，如果一个数 j>ij>i 且 aj≤aia_j\le a_i，那它就对于所有小于 ii 的位置没用了。
证明：对于一个 k<ik<i，如果 ak<aja_k<a_j，那么 aia_i 比 aja_j 更优，如果 aj≤ak<aia_j\le a_k<a_i，那么 aja_j 就不会被考虑了，而 aia_i 会，如果 ai≤aka_i\le a_k，那么两个位置都不会被考虑。所以 ii 一定不劣于 jj。
考虑倒着扫，扫的过程中我们发现没被排除的状态的值一定是随着位置而单调增的。
所以加入状态时我们只用将位置最小的那一些比 ii 劣的状态排除了。
如何计算答案呢，我们发现，好像可以在那些状态中二分计算。
但其实考虑最优的状态是什么，比 ii 大的第一个数，刚好就是用 ii 排除完那一些比 ii 劣的状态后，位置最小的那一个状态啊。
这样每个状态最多被加入一次，被排除一次，时间复杂度 O(n)\mathcal{O}(n)。
我们发现因为每次只会将那些位置最小的依次排除，而位置最小的那些状态一定是最后加入的，所以需要维护一个先进先出的数据结构，那就是栈，而因为这个栈里维护的东西是单调的，所以被称为单调栈。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int s; 
char ch;
inline int read(){
    s=0; ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)){s=(s<<3)+(s<<1)+ch-'0';ch=getchar();}
    return s;
}
inline void write(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0'); return;
}
const int N=3e6+5;
int n,a[N],top,st[N],ans[N];
int main(){
	n=read();
    for(int i=1; i<=n; i++){
        a[i]=read();
        while(top>0 and a[st[top]]<a[i]) ans[st[top--]]=i;
        st[++top]=i;
    }
    for(int i=1; i<=n; i++) write(ans[i]),putchar(' ');
	return 0;
}

例题 7

笛卡尔树。
学过 treap 的同学都知道，这是想让你建一棵 treap。
考虑一个暴力算法，将这个序列的最大数 pkp_k 设为根，你会发现，这个数左子树就是它左边的序列所生成的笛卡尔树，右子树就是它右边的序列所生成的笛卡尔树，所以这就可以划分子问题了。
如果 pp 单调递增，此算法时间复杂度 O(n2)\mathcal{O}(n^2)，pp 随机生成，算法复杂度期望 O(nlog⁡n)\mathcal{O}(n\log n)。
有没有更优秀的算法，我们可以尝试依次插入。
因为编号递增，所以每次插入的数尽量要往右插入的，所以我们可以尝试在每次插入的树根一直走到右儿子的链。
考虑在这条链的最右端插入，如果不满足小根堆性质时，我们可以将这条链变一下。
如下图：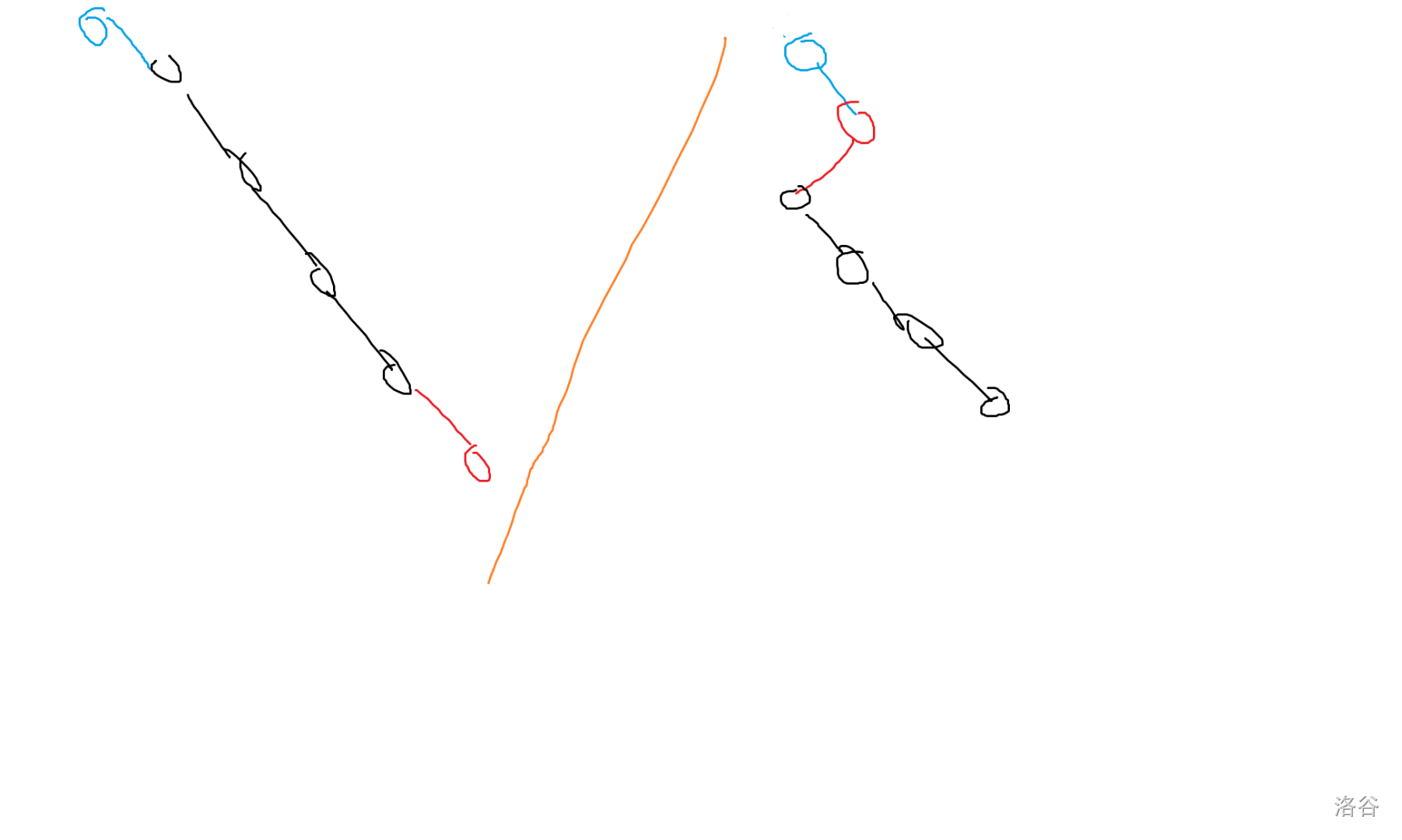
按照这样更新左右儿子就可以做到 O(n)\mathcal{O}(n)。
我们发现每次我们只用在链尾删数，插数，维护单调性，于是用单调栈维护链就行了。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10000010];
int st[10000010],top;
int l[10000010],r[10000010];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++){
		int t=top;
		while(top>0 && a[st[top]]>a[i]) top--;
		if(top) r[st[top]]=i;
		if(top<t) l[i]=st[top+1];
		st[++top]=i;
	}
	long long ans[2]={0,0};
	for(long long i=1;i<=n;i++) ans[0]^=i*(l[i]+1),ans[1]^=i*(r[i]+1);
	cout<<ans[0]<<" "<<ans[1];
	return 0;
}

例题 8

玉蟾宫。
可以先枚举底边的行数，可以递推求出那行每个数能向上延伸的长度，然后这就转化为了求一个在这个图形里的矩阵，设第 ii 个位置向上延伸了 hih_i 的距离。
考虑对每个位置作为结尾求出最大子矩阵的面积。
而一个左端点是一个可以取的左端点，它的左边那一个数的高度必须小于它。
所以说可取的位置的高度是单调递增的，可以用单调栈维护。
可以在一个状态弹栈时统计答案。
这道题就做完了。
代码CPP
#include<iostream>
#include<stack>
#include<cstring>

#define N 1010

using namespace std;

int n,m,f[N][N],maxx;
char c;
struct node {
	int len,h;
} a[N];
stack<node> S;

void ask(int x) {
	memset(a,0,sizeof(a));
	a[1].h=f[x][1],a[1].len=1;
	while(S.size())  S.pop();
	S.push(a[1]);//初始化
	for(int i=2; i<=m; i++) {
		int w=0;
		while(S.size()&&f[x][i]<=S.top().h) { //需要弹栈
			w+=S.top().len;
			maxx=max(maxx,w*S.top().h);
			S.pop();//更新答案并弹栈
		}
		a[i].h=f[x][i],a[i].len=w+1;//已入栈的比他高的矩形个数加1
		S.push(a[i]);
	}
	int w=0;
	while(S.size()) { //用剩余矩形更新答案
		w+=S.top().len;
		maxx=max(maxx,S.top().h*w);
		S.pop();
	}
}

int main() {
	cin>>n>>m;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=m; j++) {
			cin>>c;
			if(c=='F')  f[i][j]=f[i-1][j]+1;
		}

	for(int i=1; i<=n; i++)  ask(i); //解决子问题

	cout<<maxx*3<<endl;//别忘了要乘3哦

	return 0;
}

队列

2.1 基本思想回顾

队列，或 FIFO 表，是一种先进先出的线性数据结构，应用队列的算法一般来说都会非常频繁地访问队头与队尾，顾名思义，一个代表队列中最先加入的元素（也是即将弹出的元素），一个代表队列中最后加入的元素（也是当前所有元素中最后才能弹出的那个）。
队列的实现方式也有许多，对我来说最常见的当然还是是一个线性数组 + 两个指针来实现。
序列实现队列CPP
int qu[N],head=1,tail; // head,tail 分别表示当前队头和队尾的下标，这里的 qu 是 1-based 序列
inline void ins(int x){ // 在队列中插入元素 x
  qu[++tail]=x;
}
inline int del(){ // 删除并返回队头
  return qu[head++];
}
inline void clear(){ // 将队列清空
  head=1, tail=0;
}
inline int size(){ // 返回当前队列内的元素个数
  return tail-head+1;
}
系统自带的 std::queue 实现队列CPP
std::queue<int> qu;
qu.front(); // 返回队头
qu.back(); // 返回队尾
qu.push(x); // 在队尾插入 x
qu.pop(); // 弹出队首元素
qu.empty(); // 返回队列是否为空
qu.size(); // 返回当前队列内的元素个数

例题 1

板子题。
请你实现一个队列，支持如下操作：
  • push(x)：向队列中加入一个数 xx。
  • pop()：将队首弹出。如果此时队列为空，则不进行弹出操作，并输出 ERR_CANNOT_POP。
  • query()：输出队首元素。如果此时队列为空，则输出 ERR_CANNOT_QUERY。
  • size()：输出此时队列内元素个数。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n,opt,x,qu[10002],tail,head=1;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>n;
	while(n--){
		cin>>opt;
		if(opt==1) cin>>qu[++tail];
		if(opt==2){
			if(tail<head) cout<<"ERR_CANNOT_POP\n";
			else head++;
		}
		if(opt==3){
			if(tail<head) cout<<"ERR_CANNOT_QUERY\n";
			else cout<<qu[head]<<"\n";
		}
		if(opt==4) cout<<tail-head+1<<"\n";
	}
	return 0;
}

2.2 普通队列思想运用

与普通栈的应用类似，普通队列的运用同样需要注重其 FIFO 的特征。

例题 2

合并果子。
合并果子，但是线性。
首先，这道题的普通贪心做法就是建一个堆，每次去最小的两堆合并。
如果要线性，最开始肯定要排序，于是可以用计数排序。
又发现一个关键性质，就是每次合并完的果子的个数是单调递增的。
排完序之后最开始果子也是单调递增的。
于是可以用两个队列维护，第一个队列维护最开始的果子，第二个维护合并过的果子。
每次在队尾插入就可以维护这个队列的单调性，每次只用在队首取最小值就行了。
代码CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,cnt,sum;
queue<int>p,q;
inline int read(){
    int s=0,f=1; char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} // 如果是标点或负号
    while(isdigit(ch)){s=(s<<3)+(s<<1)+ch-'0';ch=getchar();} // 如果是数字
    return s*f;
}
inline int get(){
    if(p.empty()){
        int t=q.front();
        q.pop();
        return t;
    }
    if(q.empty()){
        int t=p.front();
        p.pop();
        return t;
    }
    int t1=q.front(),t2=p.front();
    if(t1<t2){
        q.pop();
        return t1;
    }
    else{
        p.pop();
        return t2;
    }
}
int buc[100010];
signed main(){
	n=read();
	for(int i=1; i<=n; i++) buc[read()]++;
	for(int i=1;i<=100000;i++) for(int j=1;j<=buc[i];j++) q.push(i);
	int ans=0; 
    for(int i=1;i<n;i++){
        int w1=get();
        int w2=get();
//        cout<<w1<<" "<<w2<<"\n";
        ans+=w1+w2;
        p.push(w1+w2);
    }
    cout<<ans;
    return 0;
}

例题 3

双端队列。
因为需要连接成一个排好序的序列，所以考虑从小到大依次加入。
在一个双端队列里，元素的下标都是单谷的，这个很好证明。
所以可以维护这个单谷的性质，但直接这样是错的。
为什么？因为有一些相等的数，而相等的数位置可能不同，而他们怎样排在双端队列里都行。
维护单谷的下标的下降段和上升段即可，新开下降段时答案加一。
代码CPP
#include <cstdio>
#include <algorithm>
int s,f;
char ch;
inline int read(){
	s=0,f=1;
    do if(ch=='-') f=-1;
	while((ch=getchar())<48);
	do s=(s<<3)+(s<<1)+(ch^48);
	while((ch=getchar())>47);
	return s*f;
}
struct node{
	int x,y;
	bool operator < (const node &p) const{
		if(x==p.x) return y<p.y;
		return x<p.x;
	}
}a[200002];
int ans=1,n,j;
signed main() {
	n=read();
	for(register int i=1; i<=n; i++) a[i]={read(),i};
	std::sort(a+1,a+1+n);
	for(register int i=1,pos=-1,pre=2e9; i<=n; i++) {  
		j=i;
		while(j+1<=n and a[i].x==a[j+1].x) j++;
		if(pos==-1) {
			if(a[j].y<pre) pre=a[i].y;
			else pos=1,pre=a[j].y;
		}else if(a[i].y>pre) pre=a[j].y;
		else ans++,pos=-1,pre=a[i].y;
		i=j;
	}
    printf("%d",ans);
	return 0;
}

2.3 单调队列

例题 4

单调队列。
像单调栈那道题一样，我们可以排除一些状态，这边以最小值为例，最大值同理。
从左往右扫右端点，我们发现，如果一个数 i<ji<j 且 ai>aja_i>a_j，那么 ii 这个数就没用了，因为 jj 绝对比 ii 优。
我们又发现，有用的数单调递增，可以考虑用单调栈维护吗？
可以的，因为栈里单调递增，每次可以在单调栈里二分第一个坐标在窗口里的数。
可以做到 O(nlog⁡n)\mathcal{O}(n\log n)。
此时我们再发现，每次窗口的左端点都会向后移动，所以我们可以将在窗口左端前面的状态全部删掉。
所以可以用一个头端可以删除，尾端既可以插入，又可以删除的队列维护。
这就是单调队列。
代码CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5;
int n,k,a[N],q[N];
inline int read(){
    int s=0,f=1; char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} // 如果是标点或负号
    while(isdigit(ch)){s=(s<<3)+(s<<1)+ch-'0';ch=getchar();} // 如果是数字
    return s*f;
}
void getmin(){
    int l=0,r=-1;
	for(int i=1; i<k; i++){ // 先传 k 个数
        while(l<=r and a[q[r]]>=a[i]) r--;
        q[++r]=i;
    } 
    for(int i=k; i<=n; i++){
        while(l<=r and a[q[r]]>=a[i]) r--;
        q[++r]=i;
        while(q[l]<=i-k) l++;
        printf("%d ",a[q[l]]);
    }
}
void getmax(){
    int l=0,r=-1;
	for(int i=1; i<k; i++){ // 先传 k 个数
        while(l<=r and a[q[r]]<=a[i]) r--;
        q[++r]=i;
    } 
    for(int i=k; i<=n; i++){
        while(l<=r and a[q[r]]<=a[i]) r--;
        q[++r]=i;
        while(q[l]<=i-k) l++;
        printf("%d ",a[q[l]]);
    }
}
signed main(){
	n=read(),k=read();
    for(int i=1; i<=n; i++) a[i]=read();
    getmin(); cout<<"\n"; getmax();
	return 0;
}

例题 5

跳房子。
先考虑二分要花费的金币数 gg。
首先，对于一个 gg，考虑 dp，列出 dp 转移式子为 dpi=max⁡j=max⁡(0,i−d−g)min(i−1,i−d+g)dpj+sidp_i=\max_{j=\max(0,i-d-g)}^{min(i-1,i-d+g)} dp_j+s_i。
尝试优化转移，这个方程可以将它看成一个长度为 2g2g 的窗口在滑动，于是每次将 dpdp 数组的值加入单调队列，就可以做了。
这就是单调队列优化 dp。
代码CPP
#include<iostream>
#define int long long
using namespace std;
int n,d,k,bl[500005][2],f[500005];
inline bool check(int g) {
	for(int i=1; i<=n; i++)f[i]=-1e18;
	f[0]=0;
	for(int i=1; i<=n; i++) {
		for(int j=i-1; j>=0; j--) {
			if(bl[i][0]-bl[j][0]>(d+g)) break;
			if(bl[i][0]-bl[j][0]<max(d-g,1ll)) continue;
			f[i]=max(f[i],f[j]+bl[i][1]);
			if(f[i]>=k) return true;
		}
	}
	return false;
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>d>>k;
	for(int i=1; i<=n; i++) cin>>bl[i][0]>>bl[i][1];
	int l=0,r=1e5+5;
	while(l<r) {
		int mid=(l+r)>>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	if(l==1e5+5) cout<<-1;
	else cout<<l;
	return 0;
}

例题 6

宝物筛选。
多重背包问题的模板，直接先暴力背包 dp，考虑优化。
加入一个物品 ii 前的 dp 数组写为 ff，加入后的写为 dpdp。
转移方程为 dpk=max⁡j=0mifk−j×wi+vi×jdp_k=\max_{j=0}^{m_i}f_{k-j\times w_i}+v_i\times j。
因为对 wiw_i 同余的状态才能互相转移，所以考虑对 wiw_i 的每个余数依次 dpdp。
设现在要处理的余数为 tt，fk′=fk×wi+tf'_{k}=f_{k\times w_i+t}，dpk′=dpk×wi+tdp'_{k}=dp_{k\times w_i+t}。
于是可以得出：
dpk′=max⁡j=max⁡(0,k−mi)kfj′+vi×(k−j)=max⁡j=max⁡(0,k−mi)kfj′−vi×j+vi×k=vi×k+max⁡j=max⁡(0,k−mi)kfj′−vi×jdp'_{k}=\max_{j=\max(0,k-m_i)}^{k} f'_{j}+v_i\times (k-j)=\max_{j=\max(0,k-m_i)}^{k} f'_{j}-v_i\times j+v_i\times k=v_i\times k+\max_{j=\max(0,k-m_i)}^{k} f'_{j}-v_i\times j
这分别进行的两个化式子分别为拆乘法和将常数提到前面。
此时我们要求 fj′−vi×jf'_{j}-v_i\times j 的最小值，我们又发现，这就是一个长度为 mim_i 的滑动窗口问题。
于是我们就可以解决了。
在这里贴一份板子供参考。
板子CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
int v[100010],w[100010],p[100010];
int dp[100010],f[100010],q[100010],head=1,tail;
signed main() {
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>p[i];
	for(int i=1;i<=n;i++){
		for(int j=0;j<=m;j++) f[j]=dp[j];
		for(int j=0;j<w[i];j++){
			head=1,tail=0;
			for(int k=j;k<=m;k+=w[i]){
				while(head<=tail && q[head]<k-w[i]*p[i]) head++;
				if(head<=tail) dp[k]=max(dp[k],f[q[head]]+(k-q[head])/w[i]*v[i]);
				while(head<=tail && f[k]>=f[q[tail]]+(k-q[tail])/w[i]*v[i]) tail--;
				q[++tail]=k;
			}
		}
	}
	cout<<dp[m];
	return 0;
}

例题 7

划分。

最初的 dp

O(n2∑i=1nai)\mathcal{O}(n^2\sum_{i=1}^na_i) 的算法是我们记录 dpi,vdp_{i,v} 为以 ii 结尾的最大价值且最后一段的和为 vv。
此时转移可以另开一段，或者延续上一段。
首先对于两个段 aa 与 bb，且 a<ba<b，显然 (a+b)2>a2+b2(a+b)^2>a^2+b^2。

用性质优化

于是需要在 a<ba<b 的情况尽量多分段，于是考虑 dp。
设 dpidp_i 为前 ii 个数的最优运行时间。
因为多分段，所以 dpidp_i 的最后一段一定最小，所以 dpidp_i 对于后买你的状态一定最优。
我们将 dpidp_i 的最后一段和记为 lil_i。
设 dpidp_i 是从 dpjdp_j 转移来的，那么 li=∑k=j+1iakl_i=\sum_{k=j+1}^ia_k。

单调队列优化

如果 dpidp_i 由 dpjdp_j 转移，设 pi=jp_i=j。
设 ss 为 aa 的前缀和数组，于是有 li=si−spil_i=s_i-s_{p_i}。
这个转移的条件有 sj−spj≤si−sjs_j-s_{p_j}\le s_i-s_j。
移项可得 si≥2sj−spjs_i\ge 2s_j-s_{p_j}。
又因为 si+1>sis_{i+1}>s_i，所以一个 jj 对于 ii 满足条件，它对于 i+1i+1 也满足条件。
于是我们建立单调队列，内装候选项。
转移时直接将不满足条件的排出，插入时将比此状态劣（也就是 2sj−spj2s_j-s_{p_j} 大的）的排出。
最后直接计算答案即可。
时间复杂度 O(n)\mathcal{O}(n)。
点个赞吧。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n,FW_number;
int a[40000010];
long long s[40000010];
inline void write(__int128 x){
	if(x<0){
		putchar('-');
		write(-x);
		return;
	}
	if(x<10){
		putchar(x%10+'0');
		return;
	}
	write(x/10);
	putchar((x%10)^48);
} 

int pre[40000010];
int q[40000010],head,tail;
int b[40000010],p[100010];
inline long long l(int x){
    return s[x]-s[pre[x]];
}
void read(){
	long long x,y,z,m;
	cin>>x>>y>>z>>b[1]>>b[2]>>m;
	for(int i=3;i<=n;i++) b[i]=(x*b[i-1]+y*b[i-2]+z)%(1<<30);
	for(int i=1;i<=m;i++){
		long long l,r;
		cin>>p[i]>>l>>r;
		for(int j=p[i-1]+1;j<=p[i];j++) a[j]=(b[j]%(r-l+1))+l;
	}
	for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
}
int main() {
	cin>>n>>FW_number;
	if(!FW_number) for(int i=1;i<=n;i++) cin>>a[i],s[i]=s[i-1]+a[i];
	else read();
	head=1,tail=0;
	q[++tail]=0;
	for(int i=1;i<=n;i++){
		while(head<tail && s[i]-s[q[head+1]]>=l(q[head+1])) head++;
		pre[i]=q[head];
		while(head<tail && s[q[tail]]-s[i]>=l(i)-l(q[tail])) tail--;
		q[++tail]=i;
	}
	__int128 ans=0;
	for(int i=n;i;i=pre[i]) ans+=(__int128)l(i)*l(i);
	write(ans);
	return 0;
}

链表

3.1 基础思想回顾

链表是一种通过指针或伪指针（存储下标来指向元素）来连接元素的线性基础数据结构。其在中间插入任意元素和在中间删除任意元素的效果非常显著（时间复杂度仅为 O(1)\mathcal{O}(1)），但是若要访问或者寻找一个元素，时间复杂度很大，为 O(n)\mathcal{O}(n)。如果要扫一遍整个链表来统计所有元素，其时间复杂度也是 O(n)\mathcal{O}(n)，故其很有实用性。
简单来说，链表是一连串“藏宝图”，每张藏宝图上都标记着下一张“藏宝图”的地址。链表还有不同的分支：单向链表、双向链表、循环链表和非循环链表，其示意图如下。
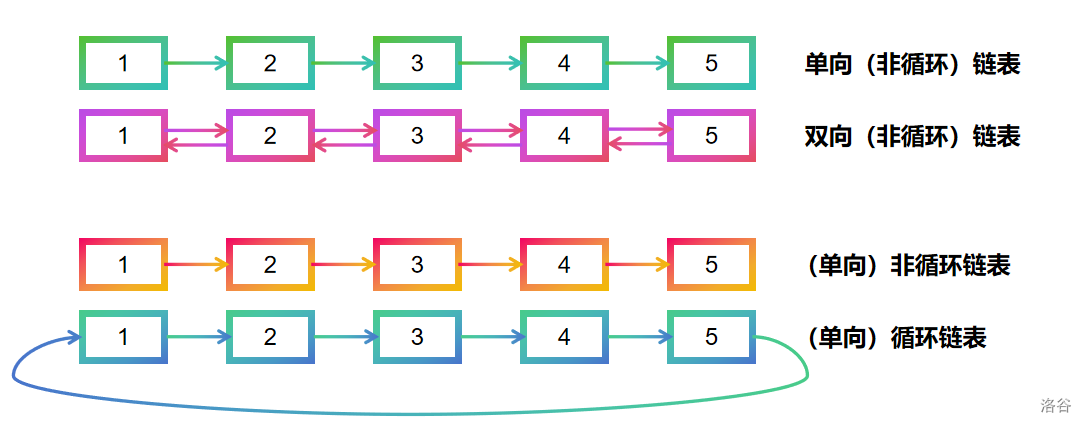
不同类型的链表有不同类型的优点，这一部分我们将在例题讲解中详细概述。
先简单说说链表的实现。一般来说，指针链表的实现靠的是结构体，结构体中每个节点都存储一个或两个指针，以及若干个需要维护的元素值。而数组链表则靠多个数组来构成，指针数组装入的数字代表其连接的元素的下标。
下文中代码的演示均以双向非循环链表为例。
链表的构建
指针写法：
CPP
struct node{
  int val;
  node *le;
  node *ri;
};
node a[114];
下标写法：
CPP
int le[114],ri[114],val[114],idx; // idx 表示元素的个数，也是最后加入的元素的编号 / 下标
链表中元素的插入
指针写法：
CPP
inline void ins(int num, node *p) {
  node *d=new node;
  d->val=num;
  d->ri=p->ri;
  p->ri=d;
  d->le=p;
  d->ri->le=d;
}
下标写法：
CPP
inline void ins(int num,int plc){
  val[++idx]=num;
  ri[idx]=ri[plc];
  ri[plc]=idx;
  le[idx]=plc;
  le[ri[idx]]=idx;
}
链表中元素的删除
指针写法：
CPP
inline void del(node *&p) {
  p->le->ri=p->ri;
  p->ri->le=p->le;
  node *t=p;
  p=p->ri;
  delete t;
}
下标写法：
CPP
inline void del(int plc){
  ri[le[plc]]=ri[plc];
  le[ri[plc]]=le[plc];
}
链表中元素的遍历
指针写法：
CPP
node *p=start;
while(p!=nullptr){
  p=p->ri;
  ...
}
下标写法：
CPP
for(int i=beg; i; i=ri[i]){
  ...
}
学会了任意一种写法，很快就能做板子。板子中提供的参考代码以下标写法为准。

例题 1

双向链表板子题。
给出 NN 个结点，编号依次为 1…N1 \dots N，初始按编号从小到大排列成一条双向链表。接下来有 MM 条指令，请按要求对链表进行修改。所有操作均保证合法。
指令含义
1 x y1\ x\ y将结点 xx 插入到 yy 的左侧（若 x=yx = y 则忽略本条指令）。
2 x y2\ x\ y将结点 xx 插入到 yy 的右侧（若 x=yx = y 则忽略本条指令）。
3 x3\ x删除结点 xx；若 xx 已被删除则忽略本条指令。
代码CPP
#include<cstdio>
#define N 500002
char ch;
inline char gc() {
    static char buf[1<<18],*p1=buf,*p2=buf;
    if(p1==p2) {
        p2=(p1=buf)+fread(buf,1,1<<18,stdin);
        if(p1==p2) return EOF;
    }
    return *p1++;
}
template<typename _Tp>
inline void read(_Tp& x) {
    x=0;
    while((ch=gc())<48);
    do x=(x<<3)+(x<<1)+(ch^48);
    while((ch=gc())>47);
}
template<typename _Tp>
inline void write(_Tp x) {
    if(x>9) write(x/10);
    putchar((x%10)^48);
}
int le[N],ri[N],n,m,sta=1,mol,x,y,del;
int main(){
	read(n), read(m);
	for(int i=1; i<=n; i++) le[i]=i-1, ri[i]=i+1;
	while(m --> 0){
		read(mol);
		if(mol==1){
			read(x), read(y);
			if(x==sta) sta=ri[sta];
			ri[le[x]]=ri[x];
			le[ri[x]]=le[x];
			le[x]=le[y];
			ri[x]=y;
			ri[le[x]]=x;
			le[ri[x]]=x;
            if(y==sta) sta=x;
		}else if(mol==2){
			read(x), read(y);
			if(x==sta) sta=ri[sta];
			ri[le[x]]=ri[x];
			le[ri[x]]=le[x];
			ri[x]=ri[y];
			le[x]=y;
			ri[le[x]]=x;
			le[ri[x]]=x;
		}else{
			read(x);
			++del;
			ri[le[x]]=ri[x];
			le[ri[x]]=le[x];
			if(x==sta) sta=ri[sta];
		}
	}
	if(del==n) puts("Empty!");
	else{
		for(int i=sta; i and i<=n; i=ri[i]){
			write(i);
			putchar(' ');
		}
	}
    return 0;
}

3.2 基于 STL 的链表实现方法

这边介绍一种 STL 容器，叫做 list，也就是链表。
它不能随机访问，但它有迭代器。
它可以支持 O(1)\mathcal{O}(1) 的 push_back，push_front，pop_back，pop_front，back，front 函数，和 O(1)\mathcal{O}(1) 的 insert 和 erase 函数。
它还有一个 merge 函数，用法：l1.merge(l2)，可以将 l2 拼接在 l1 后面。
这个容器常数有点大，但是使用队列时可以通过 queue<int,list<int> >q 来省空间。（因为普通的 queue 的底层容器为 deque，空间占用大，时间占用也大，当然 stack 同理）

3.3 链表的应用

链表的插入与删除如此简单，再加上合并两个链表（一个尾接上一个首）出奇容易，所以这种可并数据结构一下子就变得非常常用。平时图论中经常提及的邻接表，就是一种典型应用。
下面，将根据这些特性，解决更多的问题。

例题 2

小熊的果篮。
思路水，但是代码很【数据删除】。
因为一个数可以在中间消失，又要统计每个块的信息，还要删块，所以考虑用链表维护每个块。
每次输出就是输出每个块的块头，然后把块头删了。
下一步操作就是删掉空的块。
最后，将相同的块合并。
用链表维护后，第一个和第二个操作都很简单，而合并怎么办呢。
继续考虑每个块也用链表维护，因为链表可以支持 O(1)\mathcal{O}(1) 合并。
可以使用 list 实现，为了让大家熟悉链表与 STL 的操作，下面放出代码。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n,a[200010];
struct node{
	int w;
	list<int>pos;
};
list<node>q;
#define iter list<node>::iterator
#define iter2 list<int>::iterator
int main() {
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	a[n+1]=114514;
	int l=1;
	for(int i=2;i<=n+1;i++) if(a[i]!=a[i-1]){
			list<int>t;
			for(int j=l;j<i;j++) t.push_back(j);
			q.push_back((node){a[l],t}),l=i;
		}
	int cnt=0; 
	while(cnt!=n){
		while(q.begin()->pos.empty()) q.pop_front();
		cout<<q.begin()->pos.front()<<" ",cnt++;
		q.begin()->pos.pop_front();
		for(iter it=next(q.begin());it!=q.end();it++){
			if(it->pos.empty()){
				iter T=next(it);
				q.erase(it);
				it=prev(T);
			}
			else if(it->w==prev(it)->w){
				list<int> K1=prev(it)->pos,K2=it->pos;
				K1.merge(K2);
				q.erase(prev(it));
				it->pos=K1;
			}
			else cout<<it->pos.front()<<" ",cnt++,it->pos.pop_front();
		}
		cout<<"\n";
	}
	return 0;
}

例题 3

邻值查找。
介绍一种常数非常大的 O(n)\mathcal{O}(n) 做法。
先排序，可以使用基数排序，然后按排序前的下标按照排完序的序列依次插入进链表里。
记录每个下标对应的链表的元素的位置来方便访问。
接着从 nn 到 22 删数，删数前就可以查询它在链表对应位置的左边的数和右边的数。
这样就可以 O(n)\mathcal{O}(n) 了，我用的 STL，所以常数非常大。
使用 STLCPP
#include<bits/stdc++.h>
using namespace std;
list<int>s;
int n,a[int(1e5)+10],b[int(1e5)+10];
int buc[310],c[int(1e5)+10];
void radix_sort(int a[],int l,int r){
    for(int i=l;i<=r;i++) a[i]+=1e9;
	int radix=0;
	for(int i=1;i<=4;i++){
		memset(buc,0,sizeof buc);
		for(int j=l;j<=r;j++) buc[(a[j]>>radix)&255]++;
		for(int j=0;j<256;j++) buc[j]+=buc[j-1];
		for(int j=r;j>=l;j--) c[l+(buc[(a[j]>>radix)&255]--)-1]=a[j];
		for(int j=l;j<=r;j++) a[j]=c[j];
		radix+=8;
	}
	for(int i=l;i<=r;i++) a[i]-=1e9;
}
unordered_map<int,int>mp;
unordered_map<int,list<int>::iterator>pos;
stack<pair<int,int> >st;
int main() {
    ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		b[i]=a[i];
		mp[a[i]]=i;
	}
	radix_sort(a,1,n);
	for(int i=1;i<=n;i++){
		s.push_back(a[i]);
		pos[a[i]]=prev(s.end());
	}
	for(int i=n;i>1;i--){
		list<int>::iterator it=pos[b[i]];
		int t1=2e9,t2=2e9;
		if(next(it)!=s.end()) t1=*next(it);
		if(it!=s.begin()) t2=*prev(it);
		int ans;
		if(t2==2e9) ans=t1;
		else if(t1==2e9) ans=t2;
		else if(abs(t1-*it)==abs(t2-*it))
			ans=t2;
		else if(abs(t1-*it)<abs(t2-*it))
			ans=t1;
		else ans=t2;
		st.push({abs(ans-*it),mp[ans]});
		s.erase(it);
	}
	while(!st.empty()) cout<<st.top().first<<" "<<st.top().second<<"\n",st.pop();
	return 0;
}

例题 4

数据备份。
互相备份的两个办公楼一定是相邻的，不然一定不优。
于是可以想到一个思路就是每次取相邻距离最小的两个点。
但这是错的，因为如果不连最小的两个，那么你可以连旁边的那两个可能更优。
于是我们又发现删掉中间那条线，变成两边的可以使连线数加一，可以考虑用反悔贪心。
如果选择连了一个线，那么可以删掉旁边两个可选的线，将选择这个线的价值变为选择旁边两条线的价值之和减去选择中间这个线的价值。每次找最优的价值的就行了。
删旁边的操作交给链表，找最优的操作交给堆，然后就做完了。
代码CPP
#include<cstdio>
#include<queue>
#define inf 2000000000
#define N 100005
int f[N],l[N],nxt[N],pre[N],n,k,ans;
struct node{int id,val;} now;
inline bool operator < (node a,node b) {return a.val>b.val;}
std::priority_queue<node> qu;
int main() {
	scanf("%d %d",&n,&k);
	for(int i=1; i<=n; i++) scanf("%d",&f[i]);
	for(int i=1; i<n; i++) l[i]=f[i+1]-f[i],nxt[i]=i+1,pre[i]=i-1;
	nxt[n-1]=0;
	for(int i=1; i<n; i++) qu.push({i,l[i]});
	for(int i=1; i<=k; i++) {
		now=qu.top(),qu.pop();
		if(now.val!=l[now.id]) {k++;continue;}
		ans+=now.val;
		int lp=pre[now.id],rn=nxt[now.id];
		nxt[now.id]=nxt[rn];
		pre[nxt[now.id]]=now.id;
		pre[now.id]=pre[lp];
		nxt[pre[now.id]]=now.id;
		l[now.id]=(lp and rn)?std::min(inf,l[lp]+l[rn]-l[now.id]):inf;
		l[lp]=l[rn]=inf;
		qu.push({now.id,l[now.id]});
	}
	printf("%lld",ans);
}

例题 5

带插入区间 K 小值。
这种带插入又带访问的可以考虑使用块状链表。
可以用一个有 N\sqrt{N} 个元素的链表，里面每个元素是一个数组，长度不超过 N\sqrt{N}，最好这个 NN 不要变动。
插入时就在对应的块里插入，如果这个块的长度超了，那么分裂这个块到这个块原来的一半。
可以证明分裂最多进行 2N2\sqrt{N} 次。
随机访问可以直接暴力枚举每个块来 O(N)\mathcal{O}(\sqrt{N}) 查询。
对于每个块我们值域分块，然后维护一个桶和一个分块的桶。
因为值域分块要区间查询，所以要记录桶的每个位置在块状链表上的前缀和。
查询就像普通值域分块一样查询就行了。
每次分裂可以暴力统计前缀和，就做完了。
为了防止大家调试太久，我贴个代码。
代码CPP
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[70010],len,MX,lmx;
template<typename type>
class GOODLIST{
	public:
	struct GOODNODE{
		GOODNODE *l,*r;
		type val;
	};
	GOODNODE *head,*tail;
	int siz;
	inline GOODLIST(){head=tail=nullptr,siz=0;}
	inline GOODNODE *new_node(type x){
		GOODNODE *p=new GOODNODE;
		p->l=p->r=nullptr,p->val=x;
		return p;
	}
	inline void push_back(type x){
		GOODNODE *p=new_node(x);
		if(siz==0) head=tail=p;
		else p->l=tail,tail->r=p,tail=p;
		siz++;
	} 
	inline void insert(GOODNODE *p,type x){//在 p 前面插入 x 
		GOODNODE *t=new_node(x);
		if(p->l!=nullptr) p->l->r=t,t->l=p->l;else head=t;
		t->r=p,p->l=t;
		siz++;
	}
	inline void erase(GOODNODE *p){
		if(p->r!=nullptr) p->r->l=p->l;else tail=p->l;
		if(p->l!=nullptr) p->l->r=p->r;else head=p->r;
		delete p;
		siz--;
	}
};
int mooncake[70010],mxojcamp[270];
struct LIST{//块状链表 + 值域分块 
	struct node{
		vector<int>v;
		int sbuc[70010],sH[270];
		inline node(){
			memset(sbuc,0,sizeof sbuc);
			memset(sH,0,sizeof sH);
			v.clear();
		}
	};
	GOODLIST<node>l;
	int SIZ;
	inline LIST(){SIZ=0;}
	inline void split(GOODLIST<node>::GOODNODE *t){//可以暴力分裂 
		node P=t->val,Q;
        int LLL=len/2;
		for(int i=LLL;i<P.v.size();i++){
			Q.v.push_back(P.v[i]);
			Q.sbuc[P.v[i]]++,Q.sH[P.v[i]/lmx]++;
			P.sbuc[P.v[i]]--,P.sH[P.v[i]/lmx]--;
		}
		while(P.v.size()>LLL) P.v.pop_back();
		for(int i=0;i<=MX;i++) Q.sbuc[i]+=P.sbuc[i];
		for(int i=0;i<=lmx+1;i++) Q.sH[i]+=P.sH[i];
		if(t->r==nullptr)
			l.erase(t),l.push_back(P),l.push_back(Q);
		else{
			GOODLIST<node>::GOODNODE *tn=t->r;
			l.erase(t),l.insert(tn,P),l.insert(tn,Q);
		}
	}
	inline void push_back(int x){
		if(l.siz==0) l.push_back(node());
		node *t=&(l.tail->val);
		(t->v).push_back(x);
		(t->sbuc)[x]++,(t->sH)[x/lmx]++;
		if((t->v).size()>2*len) split(l.tail);
		SIZ++;
	}
	inline void insert(int pos,int x){
		if(pos>SIZ){
			push_back(x);
			return;
		}
		int S=0;
		GOODLIST<node>::GOODNODE *it=l.head;
		while(S+(it->val).v.size()<pos) S+=(it->val).v.size(),it=it->r;
		(it->val).v.insert((it->val).v.begin()+pos-S-1,x);
		GOODLIST<node>::GOODNODE *IT=it;
		while(it!=nullptr){
			(it->val).sbuc[x]++,(it->val).sH[x/lmx]++;
			it=it->r;
		} 
		if((IT->val).v.size()>2*len) split(IT);
		SIZ++;
	}
	inline void update(int pos,int x){
		int S=0;
		GOODLIST<node>::GOODNODE *it=l.head;
		while(S+(it->val).v.size()<pos) S+=(it->val).v.size(),it=it->r;
		int dashena=(it->val).v[pos-S-1];
		(it->val).v[pos-S-1]=x;
		while(it!=nullptr){
			(it->val).sbuc[dashena]--,(it->val).sH[dashena/lmx]--;
			(it->val).sbuc[x]++,(it->val).sH[x/lmx]++;
			it=it->r;
		} 
	}
	inline int ask(int L,int R,int k){
		int S=0;
		GOODLIST<node>::GOODNODE *b=l.head;
		while(S+(b->val).v.size()<L) S+=(b->val).v.size(),b=b->r;
		L-=(S+1); 
		S=0;
		GOODLIST<node>::GOODNODE *e=l.head;
		while(S+(e->val).v.size()<R) S+=(e->val).v.size(),e=e->r;
		R-=(S+1);
		if(b==e){
			for(int i=L;i<=R;i++) mooncake[(b->val).v[i]]++,mxojcamp[(b->val).v[i]/lmx]++;
			int sum=0;
			for(int i=0;i<=lmx+1;i++){
				if(sum+mxojcamp[i]>=k){
					for(int j=i*lmx;j<=(i+1)*lmx-1;j++) if(sum+mooncake[j]>=k){
						for(int i=L;i<=R;i++) mooncake[(b->val).v[i]]=0,mxojcamp[(b->val).v[i]/lmx]=0;
						return j;
					}else sum+=mooncake[j];
				}
				else sum+=mxojcamp[i];
			}
			for(int i=L;i<=R;i++) mooncake[(b->val).v[i]]=0,mxojcamp[(b->val).v[i]/lmx]=0;
			return 0;
		}
		GOODLIST<node>::GOODNODE *B=b,*E=e;
		e=e->l;
		for(int i=L;i<(B->val).v.size();i++)
			mooncake[(B->val).v[i]]++,mxojcamp[(B->val).v[i]/lmx]++;
		for(int i=0;i<=R;i++)
			mooncake[(E->val).v[i]]++,mxojcamp[(E->val).v[i]/lmx]++;
		int sum=0;
		for(int i=0;i<=lmx+1;i++){
			if(sum+(e->val).sH[i]-(b->val).sH[i]+mxojcamp[i]>=k){
				for(int j=i*lmx;j<=(i+1)*lmx-1;j++) if(sum+(e->val).sbuc[j]-(b->val).sbuc[j]+mooncake[j]>=k){
					for(int i=L;i<(B->val).v.size();i++) mooncake[(B->val).v[i]]=0,mxojcamp[(B->val).v[i]/lmx]=0;
					for(int i=0;i<=R;i++) mooncake[(E->val).v[i]]=0,mxojcamp[(E->val).v[i]/lmx]=0;
					return j;
				}else sum+=(e->val).sbuc[j]-(b->val).sbuc[j]+mooncake[j];
			}
			else sum+=(e->val).sH[i]-(b->val).sH[i]+mxojcamp[i];
		}
		for(int i=L;i<(B->val).v.size();i++) mooncake[(B->val).v[i]]=0,mxojcamp[(B->val).v[i]/lmx]=0;
		for(int i=0;i<=R;i++) mooncake[(E->val).v[i]]=0,mxojcamp[(E->val).v[i]/lmx]=0;
	}
}s;
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
    MX=70000,lmx=len=sqrt(70000);
	for(int i=1;i<=n;i++) s.push_back(a[i]);
	cin>>m;
	int lans=0;
	while(m--){
		char opt;
		cin>>opt;
		if(opt=='Q'){
			int l,r,k;
			cin>>l>>r>>k;
			l^=lans,r^=lans,k^=lans;
			cout<<(lans=s.ask(l,r,k))<<"\n";
		}
		if(opt=='M'){
			int x,v;
			cin>>x>>v;
			x^=lans,v^=lans;
			s.update(x,v);
		}
		if(opt=='I'){
			int x,v;
			cin>>x>>v;
			x^=lans,v^=lans;
			s.insert(x,v);
		}
	}
	return 0;
}

//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
//aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

评论

共 6 条评论，欢迎与作者交流。

正在加载评论...