P11832 [省选联考 2025] 图排列题解

一步步分析这题怎么做。

树

手玩几组样例，发现几个性质：

一个子树内的点一定是答案排列上连续的一段。
每次贪心取子树内编号最小的节点所在的子树一定最优。

首先我们说一下性质 1，如果

u

子树的点被分成了两段，那么肯定会出现

a_i<a_j<b_i<b_j

，如图所示：

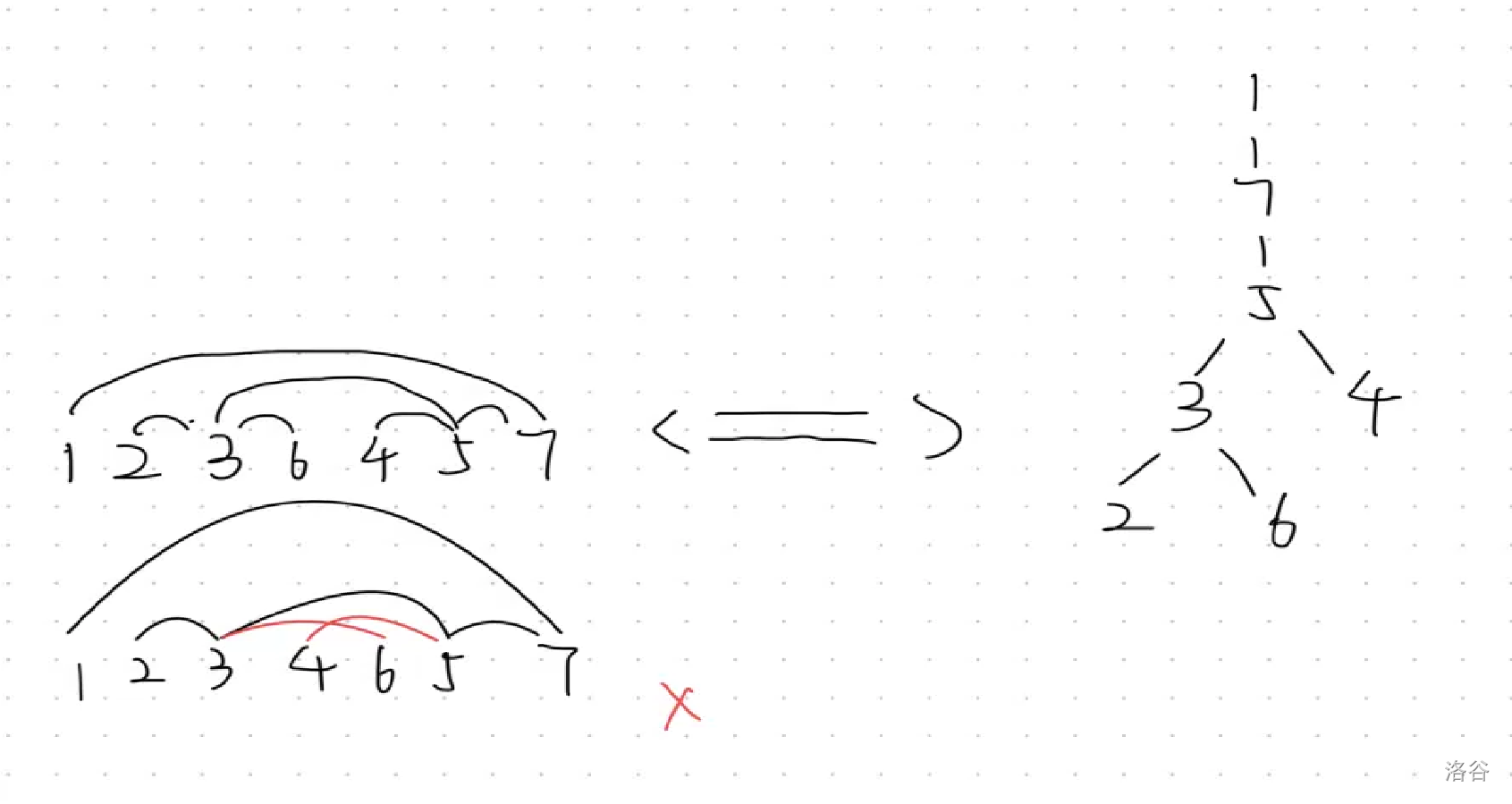
因此，我们树部分的算法如下：

处理出每个节点子树内编号最小的节点。
将儿子按子树内编号最小的节点排序。
从根开始，如果根小于所有未被加入答案的点，将根加入答案，否则，递归搜索子树。

森林

发现，我们可以将一棵树的答案随意地插入另一棵树的答案，如图所示：

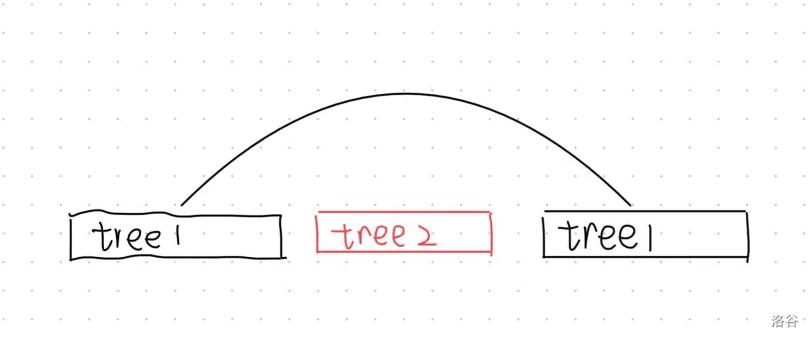并且，我们发现这个结论可以拓展到连通块。

环

发现，一个简单环

(r_1,r_2)(r_2,r_3)\dots (r_n,r_1)

，如果确定了第一个点

r_1

，那么只会有两种合法的答案排列：

$r_1\rightarrow r_n\rightarrow r_{n-1}\rightarrow \cdots \rightarrow r_2$
$r_1\rightarrow r_2\rightarrow r_3\rightarrow \cdots \rightarrow r_n$

如果我们把环拍扁，大概长这样：

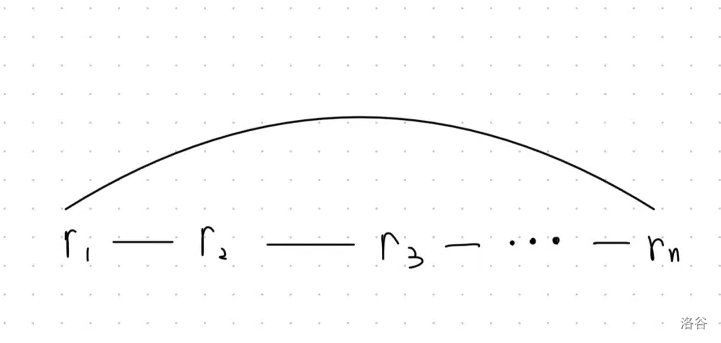
因此，我们只需要对于环找到编号最小的节点，然后看一下用上面哪种方式遍历更优即可。（仔细看了一下好像没有环的分）

连通图

发现连通图难搞的是一个点挂了很多个简单环，或者简单环复合上简单环的 Case。

于是我们考虑建出圆方树，对于原点 / 方点，分类讨论：

如果一个点是圆点，那么它上面挂的所有点双可以按任意顺序遍历，这部分直接处理出子树内编号最小的点，和树的情况一样处理即可。
如果一个点是方点，那么它连接的所有圆点形成了一个极大点双连通分量，我们的任务是将这个极大点双连通分量整理成一个环。因为保证有解，所以这个极大的环一定不存在交叉的边，这个可能有点抽象，比如说我们有这样一个环： $(r_1,r_2)(r_2,r_3)\dots (r_n,r_1)$ 那么如果存在交叉的边，那么它一定形如 $a<b<c<d,(r_a,r_c),(r_b,r_d)$ ，所以点双的边一定不会有交。

对于点双上的每一个点，都是独立的，也就是说，所以直接按照树一样做就好了。

那么对于方点，我们的任务是找到最外面这些红色的边，换言之，我们需要找到这个点双的一条哈密顿回路，一般来说这东西是 NP 的，但是这个图是一个串并联图，所以我们可以通过不断缩二度点，如果遇到重边就直接将它删去，时间复杂度 $O(T(n+m)\log n)$ 。

代码

CPP

#include "bits/stdc++.h"
const int maxn=2e5+5;
using namespace std;
vector<int> G[maxn],T[maxn],ans[maxn];
vector<array<int,2> > e[maxn];
priority_queue<int,vector<int>,greater<int> > q;
set<int> adj[maxn];
int dfn[maxn],low[maxn],stk[maxn],fa[maxn],mn[maxn],deg[maxn],top,cnt,n,m,scc;
void dfs(int u) {
    dfn[u]=low[u]=++cnt; stk[++top]=u;
    for(int v:G[u])  {
        if(dfn[v]) low[u]=min(low[u],dfn[v]);
        else {
            dfs(v); low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]) {
                fa[++scc]=u; T[scc].clear();
                T[u].push_back(scc); e[scc].clear();
                do {
                    T[scc].push_back(stk[top]);
                    fa[stk[top]]=scc; 
                } while(stk[top--]!=v);
            }
        }
    }
}
inline void tran(int o) {
    if(T[o].size()==1) return;
    stk[top=1]=fa[o]; adj[fa[o]].clear();
    for(int v:T[o]) stk[++top]=v,adj[v].clear();
    for(auto t:e[o]) {
        if(t[0]>t[1]) swap(t[0],t[1]);
        ++deg[t[0]]; ++deg[t[1]];
        adj[t[0]].insert(t[1]); adj[t[1]].insert(t[0]);
    }
    queue<int> q; T[o].clear(); set<array<int,2> > ban;
    for(int i=1;i<=top;++i) if(deg[stk[i]]<3) q.push(stk[i]);
    while(!q.empty()) {
        int u=q.front(); q.pop();
        if(!deg[u]) continue;
        if(deg[u]==1) {
            int v=*adj[u].begin();
            adj[v].erase(u); adj[u].clear();
            if(--deg[v]<3) q.push(v);
        } else {
            int v=*adj[u].begin(),w=*(++adj[u].begin());
            adj[v].erase(u); adj[w].erase(u); adj[u].clear();
            if(!adj[v].count(w)) {
                adj[v].insert(w); adj[w].insert(v);
            } else {
                if(v>w) swap(v,w); ban.insert({v,w});
                if(--deg[v]<3) q.push(v);
                if(--deg[w]<3) q.push(w);
            }
        } deg[u]=0;
    }
    for(auto t:e[o]) if(!ban.count(t)) {
        adj[t[0]].insert(t[1]); adj[t[1]].insert(t[0]);
    }
    int u=0,v=0;
    for(int i=1;i<=top;++i) if(adj[stk[i]].size()==1) {
        if(u) v=stk[i]; else u=stk[i];
    }
    if(u) adj[u].insert(v),adj[v].insert(u);
    for(int u=*adj[fa[o]].begin(),f=fa[o];u!=fa[o];) {
        T[o].push_back(u); int v=u;
        if(*adj[u].begin()==f) u=*(++adj[u].begin());
        else u=*adj[u].begin(); f=v;
    }
    for(int i=1;i<=top;++i) adj[stk[i]].clear();
    if(mn[T[o][0]]>mn[T[o].back()]) reverse(T[o].begin(),T[o].end());
}
void sol(int u) {
    if(u<=n) mn[u]=u;
    for(int v:T[u]) sol(v);
    if(u<=n) {
        sort(T[u].begin(),T[u].end(),[&](int a,int b){return mn[a]<mn[b];});
        if(T[u].size()) mn[u]=min(mn[u],mn[T[u][0]]);
    } else {
        tran(u); mn[u]=mn[T[u][0]];
    }
}
void calc(int rt,int u) {
    bool fg=0;
    for(int v:T[u]) {
        if(mn[v]>u&&!fg) ans[rt].push_back(u),fg=1;
        calc(rt,v);
    }
    if(u<=n&&!fg) ans[rt].push_back(u);
}
void out(int u) {
    q.pop();
    for(int v:ans[u]) {
        while(!q.empty()&&v>q.top()) out(q.top());
        cout<<v<<" ";
    }
    ans[u].clear();
}
inline void sol() {
    cin>>n>>m; cnt=0; scc=n;
    for(int i=1;i<=n;++i) G[i].clear(),T[i].clear(),deg[i]=dfn[i]=low[i]=0;
    for(int i=1;i<=m;++i) {
        int u,v; cin>>u>>v;
        G[u].push_back(v); G[v].push_back(u);
    }
    for(int i=1;i<=n;++i) if(!dfn[i]) {
        top=fa[i]=0; dfs(i);
    }
    for(int u=1;u<=n;++u) {
        for(int v:G[u]) if(u<v) {
            if(fa[u]==fa[v]) e[fa[u]].push_back({u,v});
            else if(fa[fa[u]]==v) e[fa[u]].push_back({u,v});
            else e[fa[v]].push_back({u,v});
        }
    }
    
    for(int u=1;u<=n;++u) if(!fa[u]) {
        sol(u); calc(u,u); q.push(u);
    }
    while(!q.empty()) out(q.top());
    cout<<'\n';
}
int main() {
//    freopen("graperm.in","r",stdin);
//    freopen("graperm.out","w",stdout);
    ios::sync_with_stdio(0);
    int c,T; cin>>c>>T; while(T--) sol();
}

P11832 [省选联考 2025] 图排列题解

文章操作

树

森林

环

连通图

相关推荐

评论

P11832 [省选联考 2025] 图排列题解