P2495 [SDOI2011] 消耗战（动态 DP 解法)

我看了一下，大部分题解都是使用的虚树，还有一小部分使用的是线段树合并，却没有任何一篇题解（甚至讨论都没有）提到题目标签中的 动态 DP 解法。

因此，我想写一篇来完整一下题解的解法。求管理大大通过。

（先自己省完题目后在来看题解）。

看完题目先推转移方程，设

f_u

表示以

u

为根的子树合法的代价，有两种从子树中转移来的方式，一种是直接断开连向儿子的边，而另一种是考虑让儿子合法，则有：

f_u=\sum_{v\in son(u)} \min(f_v,w(u,v))

w(u,v)

表示

u

到

v

的这条边的权值。

特别的，如果

u

是有能源的点，则

f_u=INF

。

发现这个 dp 的形式很动态 DP。

将轻重儿子贡献分离。

设

lightson(x)

表示

x

的轻儿子集合，

wson(x)

表示

x

的重儿子。

g_u=\sum_{v\in lightson(u)} \min(f_v,w(u,v))\\ f_u=g_u+ \min(f_{wson(u)},w(u,wson(u)))

然后转成矩阵形式：

\begin{bmatrix} g_u&g_u+w(u,wson(u))\\ INF&0\\ \end{bmatrix} \begin{bmatrix} f_{wson(u)}\\ 0 \end{bmatrix}= \begin{bmatrix} f_u\\ 0 \end{bmatrix}

非常顺利，然后上个全局平衡二叉树来维护这个转移即可。

坑点：

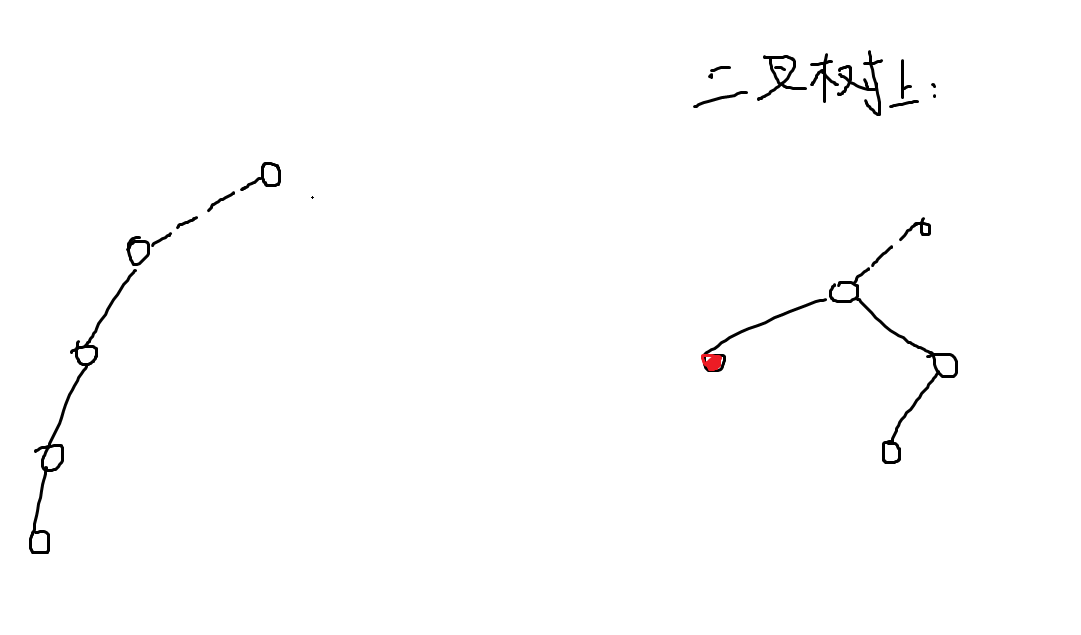
1. 本题记得开 long long，那么 INF 就要设大一些，就不要设成

10^9

这种 int 范围的极限了。

2. 本题让当前节点变成无解的方式参考保卫王国，坑点参考讨论区，作者本人用的是最简单的加减 INF 的办法（个人认为）。

3. 也是最重要的一点，一条重链转换成全局平衡二叉树时（虚边代表轻边，实边代表重边），在修改对轻父亲（对于一条轻边，深度较大的点的轻父亲为深度较小的点）贡献时，断开的边应该是标红的点连向父亲的边，而不是现在二叉树上的根连向父亲的边。如果你脑子一抽很容易写错，是谁写错了我不说（狗头）。

然后代码也不难写，并且一大半都是板子：

CPP

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int inf=1e13;
const int N=250010;
struct mat{
	int a[2][2];
	mat(){for(int i=0;i<2;i++) for(int j=0;j<2;j++) a[i][j]=inf;}
	mat operator * (const mat &b)const{
		mat res;
		for(int i=0;i<2;i++)
			for(int j=0;j<2;j++)
				for(int k=0;k<2;k++) res.a[i][j]=min(res.a[i][j],a[i][k]+b.a[k][j]);
		return res;
	}
}val[N],tr[N];
int n,siz[N],son[N],m,rt,fa[N],pre[N],b[N],ls[N],rs[N],sonw[N],faw[N],fat[N],zs[N];
vector<pair<int,int>> ed[N];
void dfs(int x,int fa){
	siz[x]=1;fat[x]=fa;
	for(auto [v,w]:ed[x]){
		if(v==fa) continue;
		faw[v]=w;
		dfs(v,x);
		siz[x]+=siz[v];
		if(siz[v]>siz[son[x]]) son[x]=v,sonw[x]=w;
	}
}
int cbuild(int cl,int cr){
	int l=cl,r=cr;
	while(l+1!=r){
		int mid=(l+r)>>1;
		if(((pre[mid]-pre[cl])<<1)<=pre[cr]-pre[cl]) l=mid;
		else r=mid;
	}
	int x=b[l];tr[x]=val[x];zs[x]=x;
	if(cl<l) ls[x]=cbuild(cl,l),fa[ls[x]]=x,tr[x]=tr[ls[x]]*tr[x],zs[x]=zs[ls[x]];
	if(l+1<cr) rs[x]=cbuild(l+1,cr),fa[rs[x]]=x,tr[x]=tr[x]*tr[rs[x]];
	return x;
}
int build(int x){
	int y=x;
	do{
		val[y].a[0][0]=val[y].a[1][1]=0;
		val[y].a[0][1]=sonw[y];
		for(auto [v,w]:ed[y]){
			if(v==son[y]||v==fat[y]) continue;
			fa[build(v)]=y;
		}
	}while(y=son[y]);
	do{
		b[y++]=x;pre[y]=pre[y-1]+siz[x]-siz[son[x]];
	}while(x=son[x]);
	return cbuild(0,y);
}
//到这里全都是板子
void change(int u,int V){
	val[u].a[0][0]+=V;val[u].a[0][1]+=V;
	while(u){
		mat pre=tr[u];
		tr[u]=val[u];
		if(ls[u]) tr[u]=tr[ls[u]]*tr[u];
		if(rs[u]) tr[u]=tr[u]*tr[rs[u]];
		if(ls[fa[u]]!=u&&rs[fa[u]]!=u){
			val[fa[u]].a[0][0]+=min(tr[u].a[0][1],faw[zs[u]])-min(pre.a[0][1],faw[zs[u]]);//这里容易写成faw[u]
			val[fa[u]].a[0][1]+=min(tr[u].a[0][1],faw[zs[u]])-min(pre.a[0][1],faw[zs[u]]);
		}
		u=fa[u];
	}
}
vector<int> U;
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<n;i++){
		int x,y,w;cin>>x>>y>>w;
		ed[x].push_back({y,w});
		ed[y].push_back({x,w});
	}
	dfs(1,0);
	rt=build(1);
	cin>>m;
	while(m--){
		int K;cin>>K;
		U.clear();
		for(int i=1;i<=K;i++){
			int u;cin>>u;
			change(u,inf);
			U.push_back(u);
		}
		cout<<tr[rt].a[0][1]<<'\n';
		for(int i=0;i<K;i++) change(U[i],-inf);
	}
	return 0;
}

P2495 [SDOI2011] 消耗战（动态 DP 解法)

文章操作

相关推荐

评论

P2495 [SDOI2011] 消耗战（动态 DP 解法)