专栏文章

题解：P5693 EI 的第六分块

ppystraf11
P5693题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@minob30e
此快照首次捕获于
2025/12/02 05:40
3 个月前
此快照最后确认于
2025/12/02 05:40
3 个月前
查看原文

Description

给定序列 a=(a1,a2,⋯ ,an)a=(a_1,a_2,\cdots,a_n)，执行 qq 次操作，分两种：
  • 1 l r k：对每个 i∈[l,r]i\in [l,r] 执行 ai←ai+ka_i\gets a_i+k。
  • 2 l r：求 max⁡(0,max⁡l≤s≤t≤r∑i=stai)\max(0,\max_{l\le s\le t\le r}\sum_{i=s}^t a_i)。

Limitations

1≤n,q≤4×1051\le n,q\le 4\times 10^5
1≤l≤r≤n1\le l\le r\le n
∣ai∣≤109,1≤k≤106|a_i|\le 10^9,1\le k\le 10^6
1.8s,256MB1.8\text{s},256\text{MB}

Solution

因为要求最大子段和，需要维护 (sum,pre,suf,ans)(\text{sum},\text{pre},\text{suf},\text{ans})，这一步很经典，不说。
然后有一个问题，区间加后，pre,suf,ans\text{pre},\text{suf},\text{ans} 的变化无法快速计算。
考虑把每个量写成一次函数 y=lx+by=lx+b，其中 ll 为所选的区间长度，那么若所选区间不变，就直接让 xx 加上 kk。
但因为 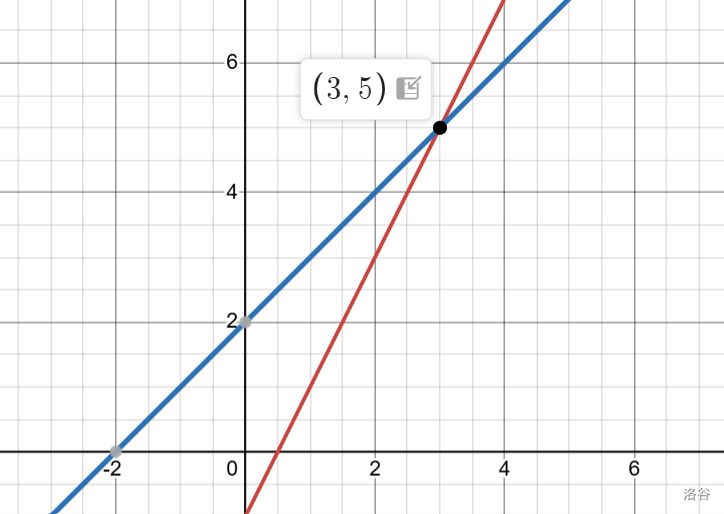pushup 时会取 max⁡\max，所选区间不是一成不变的，有时会遇到下面情况：
在 x<3x< 3 时蓝色更优，但 x>3x>3 时红色更优。
所以我们要维护当前 xx 到交点的距离 TT（若交点的 xx 坐标小于 00 或不交则视为 ∞\infty），每次修改将 TT 减去 kk，当 T<0T< 0 时，所选函数会变化，需要重构整棵子树。为了正确性，交点需要取 pushup 时所有取 max⁡\max 决策中最小的（还要包括两棵子树的 TT）。
剩下的和普通线段树一样，做完了。
根据 kk 为正数的性质，用势能分析可得时间复杂度约为 O(qlog⁡3n)O(q\log^3n)，然而卡不满，所以能过。
codeCPP
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using ui64 = unsigned long long;
using i128 = __int128;
using ui128 = unsigned __int128;
using f4 = float;
using f8 = double;
using f16 = long double;

template<class T>
bool chmax(T &a, const T &b){
	if(a < b){ a = b; return true; }
	return false;
}

template<class T>
bool chmin(T &a, const T &b){
	if(a > b){ a = b; return true; }
	return false;
}

namespace Fastio {}
using Fastio::qin;
using Fastio::qout;

constexpr i64 inf = 4e18;

struct line {
    int k; i64 b;
    inline line() : line(0, 0) {}
    inline line(int _k, i64 _b): k(_k), b(_b) {}
    inline void add(i64 v) { b += k * v; }
};

inline line operator+(const line& lhs, const line& rhs) {
    return line(lhs.k + rhs.k, lhs.b + rhs.b);
}

inline pair<line, i64> _max(const line& a, const line& b) {
    if (a.k < b.k || (a.k == b.k && a.b < b.b)) return _max(b, a);
    if (a.b >= b.b) return make_pair(a, inf);
    return make_pair(b, (b.b - a.b) / (a.k - b.k));
}

struct info {
	line pre, suf, ans, sum;
	i64 x;
	inline info() {}
	inline info(line pre, line suf, line ans, line sum, i64 x)
	    : pre(pre), suf(suf), ans(ans), sum(sum), x(x) {}
};

inline info operator+(const info& a, const info& b) {
	i64 x0 = min(a.x, b.x);
	line sum = a.sum + b.sum;
	auto [pre, x1] = _max(a.pre, a.sum + b.pre);
	auto [suf, x2] = _max(b.suf, a.suf + b.sum);
	auto [tmp, x3] = _max(a.ans, b.ans);
	auto [ans, x4] = _max(tmp, a.suf + b.pre);
	return info(pre, suf, ans, sum, min({x0, x1, x2, x3, x4}));
}

inline void operator+=(info& a, i64 v) {
	a.x -= v;
    a.pre.add(v), a.suf.add(v);
    a.sum.add(v), a.ans.add(v);
}

struct node {
    int l, r;
    info dat;
    i64 tag;
};

inline int ls(int u) { return 2 * u + 1; }
inline int rs(int u) { return 2 * u + 2; }

struct ktt {
	vector<node> tr;
	inline ktt() {}
	inline ktt(const vector<i64>& a) {
		const int n = a.size();
		tr.resize(n << 1);
		build(0, 0, n - 1, a);
	}
	
	inline void pushup(int u, int mid) { tr[u].dat = tr[ls(mid)].dat + tr[rs(mid)].dat; }
	inline void apply(int u, i64 v) { tr[u].tag += v, tr[u].dat += v; }
	
	inline void pushdown(int u, int mid) {
	    if (tr[u].tag) {
	        apply(ls(mid), tr[u].tag);
	        apply(rs(mid), tr[u].tag);
	        tr[u].tag = 0;
	    }
	}
	
	inline void build(int u, int l, int r, const vector<i64>& a) {
	    tr[u].l = l, tr[u].r = r;
	    if (l == r) {
	        line f(1, a[l]);
	        tr[u].dat = info(f, f, f, f, inf);
	        return;
	    }
	    
	    const int mid = (l + r) >> 1;
	    build(ls(mid), l, mid, a);
	    build(rs(mid), mid + 1, r, a);
	    pushup(u, mid);
	}
	
	inline void defeat(int u, i64 v) {
        const int mid = (tr[u].l + tr[u].r) >> 1;
	    if (v > tr[u].dat.x) {
	        defeat(ls(mid), tr[u].tag + v);
	        defeat(rs(mid), tr[u].tag + v);
	        tr[u].tag = 0;
	        pushup(u, mid);
	    }
	    else apply(u, v);
	}
	
	inline void update(int u, int l, int r, i64 v) {
	    if (l <= tr[u].l && tr[u].r <= r) return defeat(u, v);
	    const int mid = (tr[u].l + tr[u].r) >> 1;
	    pushdown(u, mid);
	    if (l <= mid) update(ls(mid), l, r, v);
	    if (r > mid) update(rs(mid), l, r, v);
	    pushup(u, mid);
	}
	
	inline info query(int u, int l, int r) {
	    if (l <= tr[u].l && tr[u].r <= r) return tr[u].dat;
	    const int mid = (tr[u].l + tr[u].r) >> 1;
	    pushdown(u, mid);
	    if (r <= mid) return query(ls(mid), l, r);
	    if (l > mid) return query(rs(mid), l, r);
	    return query(ls(mid), l, r) + query(rs(mid), l, r);
	}
	
	inline void range_add(int l, int r, i64 v) { update(0, l, r, v); }
	inline i64 range_gss(int l, int r) { return max(query(0, l, r).ans.b, 0LL); }
};

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	int n, m;
	qin >> n >> m;
	
	vector<i64> a(n);
	for (int i = 0; i < n; i++) qin >> a[i];
	
	ktt tree(a);
	for (int i = 0, op, l, r; i < m; i++) {
	    qin >> op >> l >> r, l--, r--;
	    
	    if (op == 1) {
	        i64 v; qin >> v;
	        tree.range_add(l, r, v);
	    }
	    else qout << tree.range_gss(l, r) << '\n';
	}
	
	return 0;
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...