专栏文章
P14507 缺零分治 mexdnc 离线解法
P14507题解参与者 3已保存评论 3
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 3 条
- 当前快照
- 1 份
- 快照标识符
- @min7j0ux
- 此快照首次捕获于
- 2025/12/01 21:50 3 个月前
- 此快照最后确认于
- 2025/12/01 21:50 3 个月前
此题题解区似乎少一个离线解法,那我发一篇
思路
- 特判没有 的情况:
- 当 答案为 。
- 当 答案为 。
设全局 为 ,那么。
- 当 答案为 。
- 当 答案为 。
- 当 答案为 。
以上结论很简单,请自行分析。
预处理
- 维护 数组。
- 我们把样例分成这样:

令
先使
再使
此时 表示以 为结尾 分割数量 。
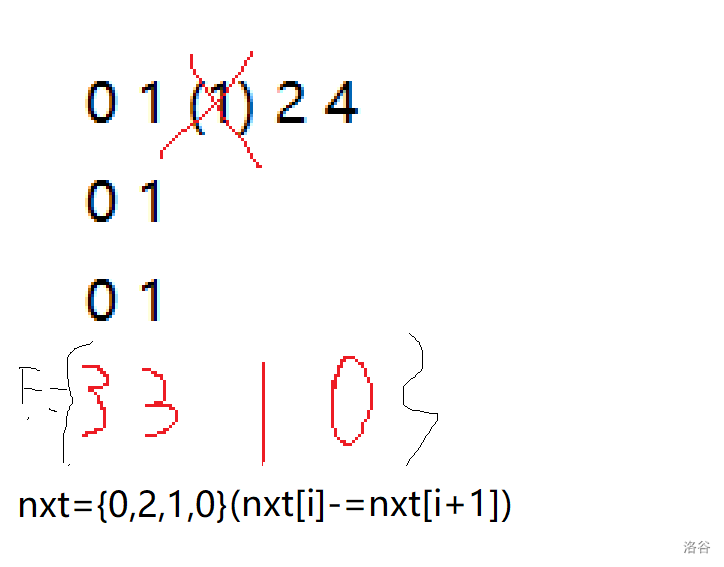 (图中 表示一开始的 )
(图中 表示一开始的 )
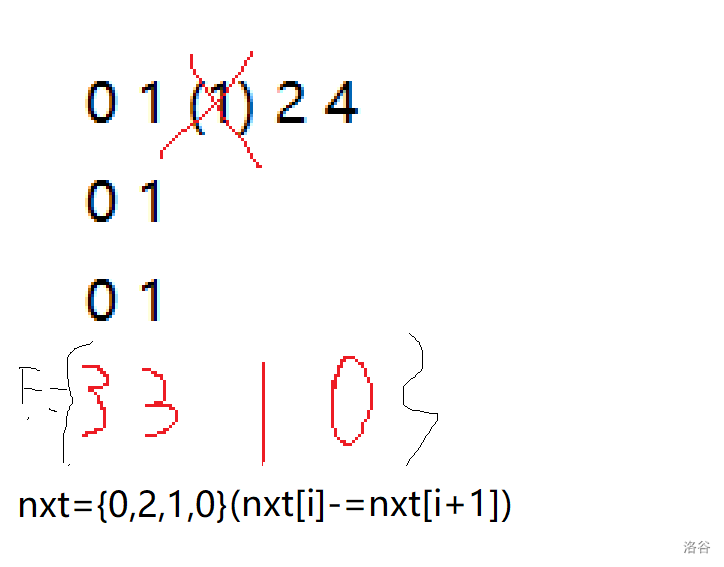 (图中 表示一开始的 )
(图中 表示一开始的 )对于
- 对于每一个询问,我们发现其答案其实就是第一行最大的 依次从长到短加其余能独立的长串,也可以只取其前缀并将未取到的并到第一行。
- 例如对于样例答案为 。
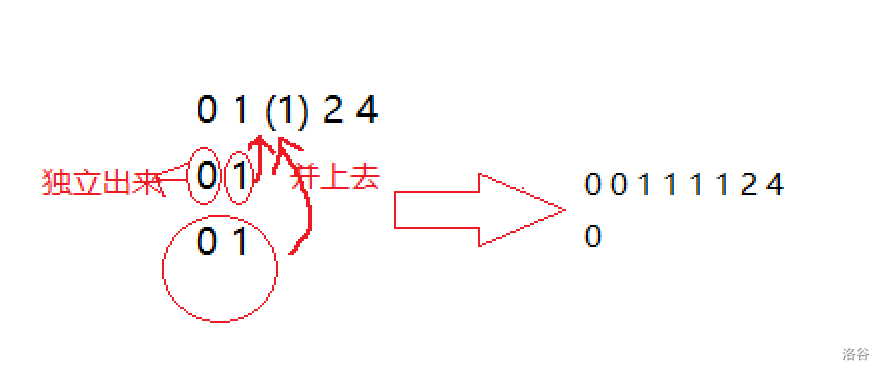
- 要是我们这么做,显然答案与 具有单调性。考虑离线维护。
- 我们将询问排个序。
- 我们一个一个并,则可能会有 个分割,会超时。
- 考虑很多分割的 是一样的,我们已经维护了。
- 以 为结尾 分割数量 。
- 所以我们每次尝试取尽量多个当前最大的分割,若能达到 那就别拿。
- 伪代码如下:
if xq<=nxt[ed]//如果最大的分割数量够
nxt[ed]-=xq
now+=ed*xq
else
now+=nxt[ed]*ed
nxt[ed]=0
ed--
(
ed 表示最大的分割的位置,)
由于分割的结尾最多有 个,所以是 。代码
C#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
template<typename T>
inline void read(T &x) {
x = 0;
register char c = getchar();
register short f = 1;
while (c < '0' || c > '9') {
if (c == '-') f = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
x *= f;
}
template <typename T, typename... Args>
inline void read(T &x, Args &...temps)
{
read(x), read(temps...);
}
void write(int x) {
static int sta[35];
int top = 0;
do {
sta[top++] = x % 10;
x /= 10;
} while (x);
while (top) putchar(sta[--top] + '0');
}
const int N=2e5+5;
struct nod{
int a,b;
}q[N];
bool cmp(nod x,nod y){
return x.a<y.a;
}
struct Q{
int x,id;
}xl[N];
bool cmp1(Q x,Q y){
return x.x<y.x;
}
int ans[N];
int nxt[N];
void solve()
{
memset(nxt,0,sizeof nxt);
memset(ans,0,sizeof ans);
memset(xl,0,sizeof xl);
memset(q,0,sizeof q);
read(n,m);
int minn=0;
for(int i=1;i<=n;i++){
read(q[i].a,q[i].b);
if(q[i].a==0){
minn=1;
}
}
int maxx=0;
int gs=0;
int tot=0;
sort(q+1,q+1+n,cmp);
int fl=1;
if(q[1].a!=0){
for(int i=1;i<=m;i++){
int x;
read(x);
if(x==0){
cout<<1;
puts("");
}
else{
cout<<-1;
puts("");
}
}
return;
}
for(int i=2;i<=n;i++){
if(q[i].a==q[i-1].a+1){
fl=max(fl,q[i].a+1);
}
else{
break;
}
}
gs=q[1].b;
maxx+=gs;
nxt[1]=gs;
int ed=1;
for(int i=2;i<=n;i++){
if(q[i].a!=q[i-1].a+1) break;
gs=min(gs,q[i].b);
nxt[i]=gs;
if(nxt[i]) ed=i;
maxx+=gs;
}
for(int i=1;i<=ed;i++){
nxt[i]-=nxt[i+1];
}
for(int i=1;i<=m;i++){
read(xl[i].x);
xl[i].id=i;
}
int now=fl;
sort(xl+1,xl+1+m,cmp1);
int bb=1;
nxt[ed]--;
for(int i=1;i<=m;i++){
if(xl[i].x>maxx){
ans[xl[i].id]=-1;
continue;
}
if(xl[i].x<minn){
ans[xl[i].id]=-1;
continue;
}
if(xl[i].x<fl){
ans[xl[i].id]=2;
continue;
}
if(xl[i].x==fl){
ans[xl[i].id]=1;
continue;
}
while(xl[i].x>now&&ed>=0){
int xq=ceil(1.0*(xl[i].x-now)/(1.0*ed));
if(xq<nxt[ed]){
now+=xq*ed;
bb+=xq;
nxt[ed]-=xq;
}
else{
now+=nxt[ed]*ed;
bb+=nxt[ed];
ed--;
}
}
if(ed<0&&xl[i].x>now){
ans[xl[i].id]=-1;
}
else ans[xl[i].id]=bb;
//if((xl[i].x-fl)/ed)
}
for(int i=1;i<=m;i++){
cout<<ans[i]<<'\n';
}
}
signed main(){
int T;
read(T);
while(T--){
solve();
}
return 0;
}
码风一坨,请批判性鉴赏~
相关推荐
评论
共 3 条评论,欢迎与作者交流。
正在加载评论...