2024.12.23 集合
符号语言
- 集合:a∈A。其中 a 是
元素,A 是集合。∈ 读作属于。
- 空集:∅。不含任何元素的集合。
- A=B 完全相同的集合。
集合性质
特殊集合
- 自然数:N
- 正整数:N+
- 整数:Z
- 有理数:Q
- 实数:R
------分割线------
- 有限集:有限个元素。
- 无限集:无限个元素。
- 空集属于有限集。
表示方法
列举法
A={元素1,元素2,元素3,⋯}
描述法
A={元素∣条件1,条件2,⋯}
列举/描述法示例
- 列举法:N={0,1,2,3,…}
- 描述法:Q={x∣x=pq,p∈Z,q∈Z}
基本关系
包含
任意
a∈A,都有
a∈B:
- A⊆B:A 包含于 B
- B⊇A:B 包含 A
A⊆B,B⊆A⟺A=B
无限集也有包含关系!
特殊情况
- A⊆A
- ∅⊆A
真包含
A⫋B:
A 真包含于
B。
任意
a∈A,都有
a∈B。存在
b∈B,满足
b∈A。则称
A 真包含于
B,即
A⫋B。
区间
- {x∣a≤x≤b}=[a,b]。
- {x∣a<x<b}=(a,b)。
- {x∣a≤x<b}=[a,b)。
- {x∣a<x≤b}=(a,b]。
至少一端无穷的区间:
- {x∣x≤b}=(−∞,b]。
- {x∣a≤x}=[a,∞)。
- R=(−∞,∞)。
韦恩图
维恩图
C⫋B,B⫋A⟹C⫋A
集合基本运算
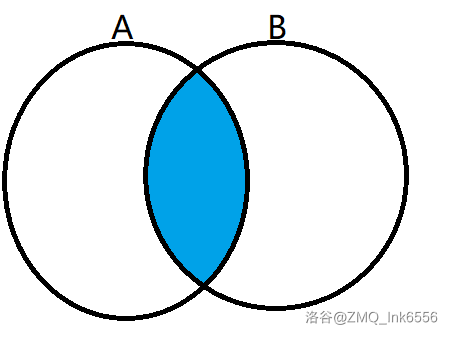
- A 和 B 的交集:A∩B。
- A∩B={x∣x∈A∧x∈B}
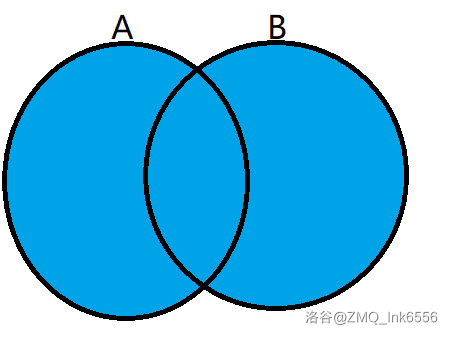
- A 和 B 的并集:A∪B。
- A∪B={x∣x∈A∨x∈B}
集合基本运算交换律
交集
- A∩B=B∪A
- A∩A=A
- A∩∅=A
- 若 A⊆B,则 A∩B=A
- A∩B∩C=A∩C∩B=B∩A∩C=B∩C∩A=C∩A∩B=C∩B∩A
并集
- A∪B=B∪A
- A∪A=A
- A∪∅=A
- 若 A⊆B,则 A∪B=B
- A∪B∪C=A∪C∪B=B∪A∪C=B∪C∪A=C∪A∪B=C∪B∪A
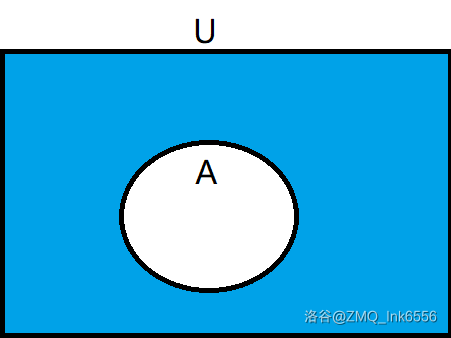
补集
∁UA=x∣x∈U,x∈A
- ∁UA∩A=∅
- ∁UA∪A=U
- ∁U(∁UA)=A
今日份闲话
x(x−1)=0,求解集。
- 正确答案:{0,1}。
- Answer1:{x∣x(x−1)=0}。
- Answer2:{x∣x=0∨x=1}。
2024.12.25 常用逻辑用语
命题
命题是基于集合的。
量词
全称量词:
存在量词:
- 任意:∀。
- 存在:∃。
- 存在且唯一:∃1。
- ∀:全真才真、一假就假。
- ∃:一真就真、全假才假。
量词命题
p(x):条件。
- 例 1:
- 任意给定实数 x,x2≥0。
- ∀x∈R,x2≥0。
- 例 2:
- 存在有理数 x,使得 3x−2=0。
- ∃x∈Q 使 3x−2=0。
否定命题
命题
P --> 否定命题
¬P。
-
若
P 为真,则
¬P 为假,否则
¬P 为真。
-
∀x∈M,P(x) --> 否定
∃x∈M,¬P(x)。
-
∃x∈M,P(x) --> 否定
∀x∈M,¬P(x)。
命题与集合
A={x∣P(x)}
使
P(x) 成立的所有的
x 组成的集合。
所有使
P(x) 成立的
x 都叫做
P(x) 的真值。
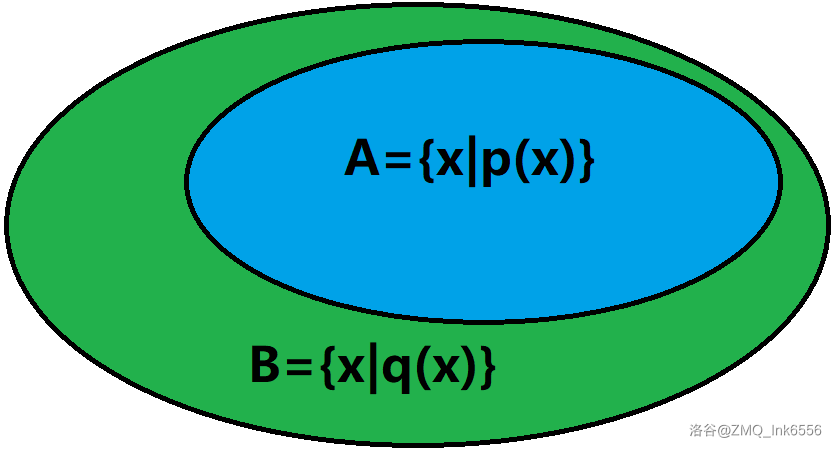
充分条件/必要条件
如果
p,那么
q。
记作
p⟹q。
p 是
q 的
充分条件。
q 是
p 的
必要条件。
如果
p 是
q 的
充分条件、
q 是
p 的
必要条件。
A={x∣p(x)},B={x∣q(x)},那么
A⊆B。
逆否命题
p⟹q 相当于
¬q⟹¬p。
-
原命题为真,逆否命题为真。
-
原命题为假,逆否命题为假。
-
- 原命题:如果 x>3,那么 x2>9。
- 逆命题:如果 x2>9,那么 x>3。
- 逆否命题:如果 x2≤9,则 x≤3。
-
- 原命题:如果 ∣x∣>3,那么 x2>9。
- 逆命题:如果 x2>9,那么 ∣x∣>3。
- 逆否命题:如果 x2≤9,则 ∣x∣≤3。
充要条件
若
p⟹q,且
q⟹p,那么
p⟺q、
q⟺p。
p⟺q 等价于
q⟺p。
- 所有判定都是充分条件。
- 所有性质都是必要条件。
- 所有定义都是充要条件。
2024.12.25 等式
等式与不等式
- 用等号(=)连接的式子叫做等式。
- 用不等号(= 等)连接的式子叫做不等式。
恒等式
推出类似公式。
(a+b)=a2+2×a×b+b2。
令
b=−b,则
(a−b)=a2−2×a×b+b2。
2024.12.27 一元二次方程
解法
例
1:
x2+6×x+8
- 十字相乘:(x+2)×(x+4)=0
- 公式法:2−6±62−4×1×8
- 配方法:(x+3)2−1=0
答案:x=−2 或 −4。
一元二次方程的解集
- 单个元素:x∈{2,3}。
- 多个元素:(x,y)∈{(1,2),(2,1)}、(a,b,c)∈{(1,2,3),(3,2,1),(2,3,1)}。
n 元一次方程
唯一解
多解的表示法
剩余
n− 本质不同的方程个数个
未知元。
例
1:
{x+2y+2z=5x−y+2z=2
{(x,y,z)∣x=3−2z,y=1,z∈R}一元二次方程解集及其根与性质的关系
ax2+bx+c=0(a=0)
- Δ=b2−4×a×c
- Δ>0:{2×a−b+Δ,2×a−b+Δ}
- Δ=0:{2×a−b}
- Δ<0:∅
韦达定理:
x1×x2=2×a−b+Δ×2×a−b+Δ=4×a2b2−Δ=4×a2b2−b2−4×a×c=ac求一元二次方程的变种
- 例 1:求 x−2x−1=0 的解集
- 解:令 x=t(t≥0),则 x=t2
- 原方程变为 t2−2t−1=0
- t=1+2 或 1−2(舍)。
- x=t2=(1+2)2=3+22
- 例 2:求 x4−x2−2=0 的解集
- 解:令 x2=t(t≥0),则 x=±t
- 原方程变为 t2−t−2=0
- t=2 或 −1 (舍)。
- x=±t=±2。
- x={−2,2}
不等式性质的推论
- 若 a>b,∀c∈R⟹a±c>b±c。
- 若 a>b,∀c∈(0,+∞)⟹ac>bc,ca>cb。
- 若 a>b,∀c∈(−∞,0)⟹ac<bc,ca<cb。
- a>b,b>c⟹a>c
- a+b>c⟹a>c−b
- a>b,c>d⟹a+c>b+d
- a>b>0,c>d>0 时 ⟹ac>bd
- 若 a>b>0,那么 an>bn(n∈N+)。
- 若 a>b>0,则 a>b。
反证法
- 已知 p,要证 q。
- 证明:假设 q 不成立(¬q 成立)
- ⋯ ⋯
- p 不成立(¬p 成立)
- ∴q 一定成立,q 得证。
证明 a<b 问题
基本方法
- 作差法:a−b<0。
- 作商法:ba<1。
其他做法
分析法:若证
⋯ ⋯ 只需证
⋯ ⋯
- 证明 3+7<25。
- 证明:若证 3+7<25 ◯ 1
- 只需证 3+7+221<20 ◯ 2
- 即 只需证 21<5 ◯ 3
- 即 只需证 21<25,自然成立。◯ 4
- ◯ 4⟹◯ 3⟹◯ 2⟹◯ 1
今日份闲话
如果你看到了这里,请
立刻新建洛谷云剪切板,输入且仅输入 LSPaintBoard-2025 ,并且将链接使用洛谷私信发给
 我
我,感谢。
如果你第一次来到这里是
2025/2/1 之后,请无视上面的话。
2025.1.12 求解一元二次不等式
不等式的解集
- 例 1 一次不等:2×x+1>5⟺2×x>4⟺x>2
- 解集:集合 {x∣x>2}
不等式组的解集
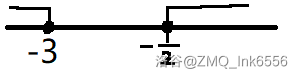
{2x+1≥0⟺2x≥−1⟺x≥−213x−2>2x+3⟺35x<−5⟺x<−3
绝对值方程
∣x∣≥3x2≥9x2−9≥0(x−3)(x+3)≥0x>3或x<−3
∣x∣≥3x>3或x<−3
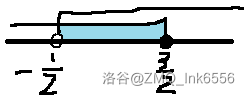
{x∣−21≤x≤23}
含有参数的不等式
2x+a>0⟺2x>−a⟺x>−2a{x∣x>−2a}
分类讨论:
- ax>1:
- 当 a=0 时,原不等式无解。
- 当 a>0 时,ax>1⟺x>a1。
- 当 a<0 时,ax>1⟺x<a1。
- ax>1 解集的表示法:
- 当 a=0 时,原不等式的解集为 ∅。
- 当 a>0 时,原不等式的解集为 {x∣x>a1}。
- 当 a<0 时,原不等式的解集为 {x∣x<a1}。
注意事项
- > 和 ≥、< 和 ≤ 不可混用。
- 不等式两边同乘一个负数要变换不等号方向。
- 开平方、绝对值等要考虑正负两种情况。
- 答案要写成集合形式。
一元二次不等式
ax2+bx+c>0(a=0)
一元二次不等式的解法
- 转换为绝对值:x2>2⟺∣x∣2>2⟺∣x∣>2。
- 分解因式:x2−4>0⟺(x+2)(x−2)>0⟺{x+2>0x−2>0或{x+2<0x−2<0⟺x>2或x<−2
大于两边分,小于中间夹。
- 若 Δ=b2−4ac<0:
- a>0:x∈R。
- a<0:∅。
- 若 Δ=b2−4ac≥0:
- a(x−x1)(x−x2)>0。
- a>0:(x−x1)(x−x2)>0。
- a<0:(x−x1)(x−x2)<0。
分式方程同乘分母时要分类讨论(正负、不为 0)。
- 若 BA>0⟺AB>0⟺(x+1)(x−1)>0⟺x>1或x<−1
2025.01.12 均值不等式
当
a,b∈R+ 时
a+b≥2ab。
当
a,b∈R 时,
a2+b2≥2ab。
当
a,b∈R 时,
2a2+b2≥ab。
推导
∀a,b∈R+
a>0,b>0⟺(a−b)2≥0⟺a2+b2−2ab≥0⟺a2+b2≥2ab
(a−b)2≥0⟺(a)2+(b)2−2ab≥0⟺a+b≥2a,b
务必检验能不能取等号
2025.01.13 函数
变量
集合与函数的关系
集合:
- x 变化范围 A
- y 变化范围 B
对于
∀x∈A,
∃1 y∈B 与之对应。
则称
f 为定义在集合
A 上的一个函数,记作
y=f(x),x∈A。
定义域:
A
值域:
{y∈B∣y=f(x),x∈A}⊆B
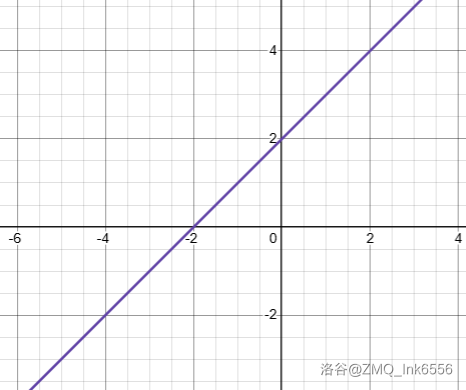
- 例 1:
- f(x)=x+2,x∈R
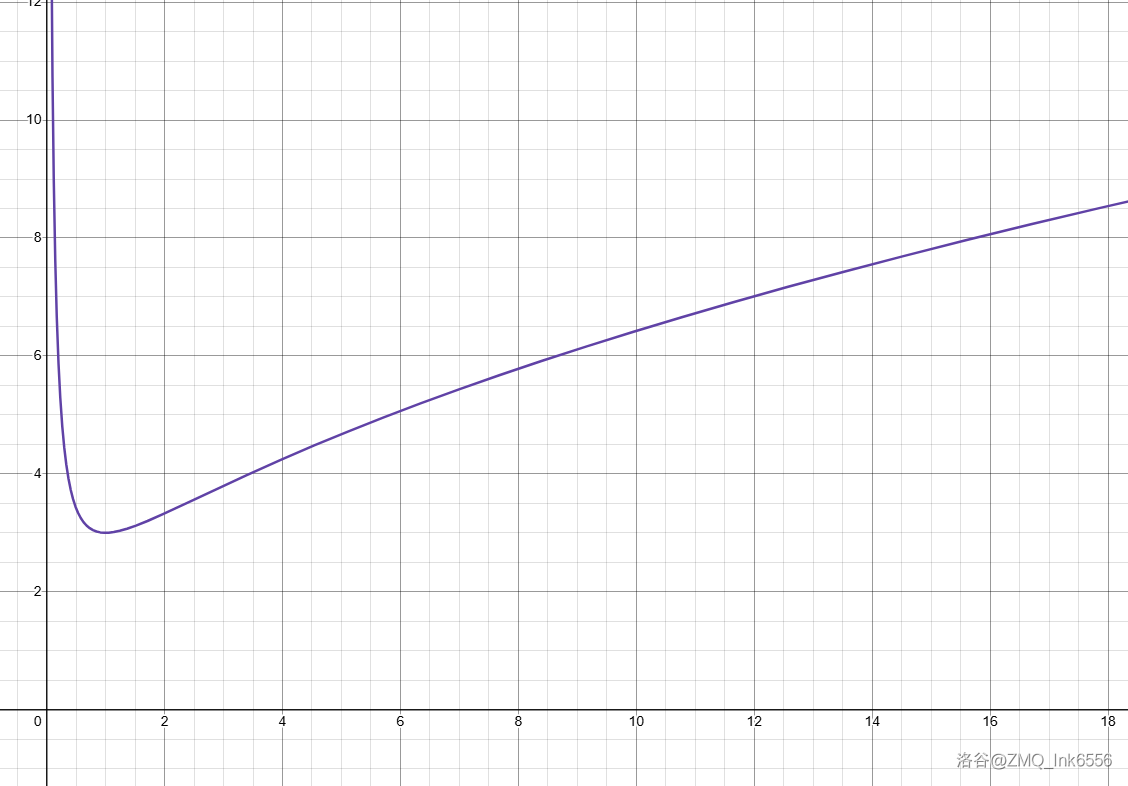
- 例 2:
- f(x)=2×x+x1,x∈R(x=0)
函数三要素:定义域、对应关系、值域。
定义域和对应关系都相同,函数才相同。
函数的表示方法
解函数题目
- 例 1:
- 已知 f(x−1)=x2,求 f(x)
- f(x−1)=(x−1)2+2(x−1)+1
- f(x)=x2+2x+1=(x+1)2
- 例 2:
- 已知 f(x)=(x−1)2,求 f(x+1)
- f(x+1)=((x+1)−1)2=x2
例 3:
- 已知 f(x+1)=(x−1)2,求 f(x)
- f(x+1)=x2−2x+1
- f(x+1)=(x+1)2−4x=(x+1)2−4(x+1)+4
- f(x)=x2−4x+4=(x−2)2
2025.01.14 函数
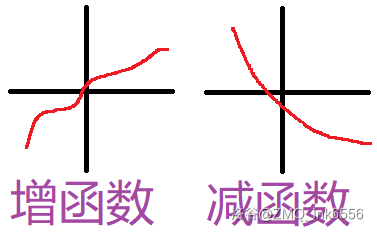
增减函数
- ∀x1,x2∈I,当 x1<x2 时,都有 f(x1)<f(x2),则称 f(x) 在 I 上是增函数(单调递增)。
- ∀x1,x2∈I,当 x1<x2 时,都有 f(x1)>f(x2),则称 f(x) 在 I 上是减函数(单调递减)。
- 例 1:
- 求证函数 f(x)=−2x 在 R 上是减函数。
- 证明:任取 x1,x2∈R,且 x1<x2 时,x2−x1>0。
- f(x1)−f(x2)=−2x1+2x22(x2−x1)>0
- 所以 f(x1)>f(x2)
- 所以 f(x)=−2x 在 R 上单调递减。
函数最值
- ∀x∈D,都有 f(x)≤f(x0),则称 f(x0) 为函数的最大值,x0 为函数的最大值点。
- ∀x∈D,都有 f(x)≥f(x0),则称 f(x0) 为函数的最小值,x0 为函数的最小值点。
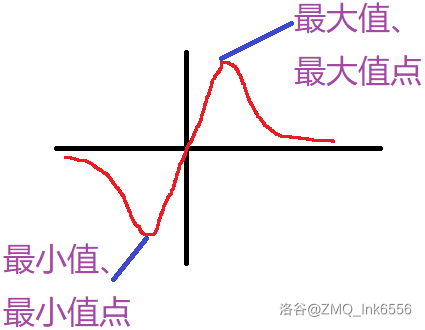
- 例 1:
- 求 f(x)=x2+3x+1 在 [−23,+∞) 上的单调性。
- 证明:任取 x1,x2∈[−23,+∞) 且 x1<x2,x1+x2+3>0,x1−x2<0。
- f(x1)−f(x2)=x12+3x1−x22−3x2
- =(x1−x2)(x1+x2)+3(x1−x2)
- =(x1−x2)(x1+x2+3)<0 且 −3<x1−x2<0
- 所以 f(x) 在 [−23,+∞) 上单调递增。
- 例 2:
- 求 f(x)=2x2+6,x∈[−5,3] 的单调区间和函数最值。
- 证明:任取 x1,x2∈[−5,−23],x1<x2
- f(x1)−f(x2)=2(x1−x2)(x1+x2+3)>0
- f(x1)>f(x2)
- 所以 f(x) 在 [−5,−23] 上单调递减。
- 任取 x1,x2∈(23,3],x1<x2
- f(x1)<f(x2)
- 所以 f(x) 在 (23,3] 上单调递增。
- f(x)min=f(−23)=−29
- f(x)max=f(3)=36
平均变化率
ΔxΔf(x)=x1−x2f(x1)−f(x2)=x2−x1f(x2)−f(x1)
- 例 1:
- 求 f(x)=x1 在 (−∞,0) 上的单调性。
- 证明:任取 x1,x2∈(−∞,0) 且 x1≥x2,x1>x2
- 则 f(x1)=x11,f(x2)=x21
- f(x1)<f(x2)
- 所以 f(x) 在 (−∞,0) 上单调递减。
函数的奇偶性
对称点:
- (x,y) 关于 x 轴的对称点为 (x,−y)
- (x,y) 关于 y 轴的对称点为 (−x,y)
- (x,y) 关于原点的对称点为 (−x,−y)
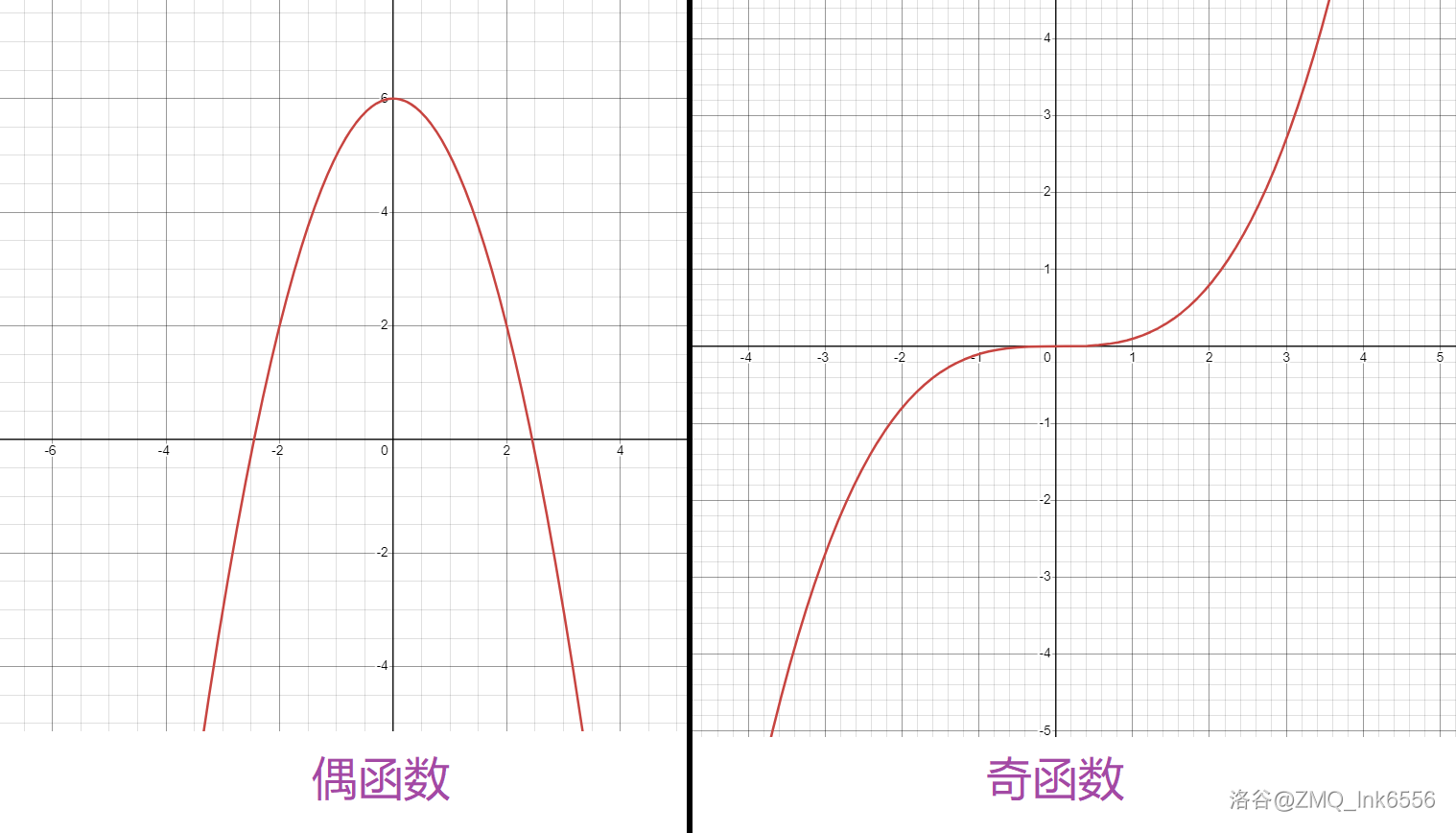
偶函数
一般地,设函数
y=f(x) 的定义域是
D,若
∀x∈D,且
f(−x)=f(x),则称
y=f(x) 是
偶函数。
- 若 (x,y) 在图像上,则 (−x,y) 也在图像上。
- 定义域 D 关于原点对称。
- 函数图像关于 y 轴对称。
偶函数
⟺ 函数图像关于
y 轴对称。
奇函数
一般地,设函数
y=f(x) 的定义域是
D,若
∀x∈D,且
f(−x)=−f(x),则称
y=f(x) 是
奇函数。
- 若 (x,y) 在图像上,则 (−x,−y) 也在图像上。
- 定义域 D 关于原点对称。
- 函数图像关于原点对称。
- f(0)=0(0 属于定义域)
奇偶关系
- 奇函数 + 奇函数 = 奇函数
- 偶函数 + 偶函数 = 偶函数
- 奇函数 × 奇函数 = 偶函数
- 偶函数 × 偶函数 = 偶函数
2025.01.15 研究函数
研究函数的方法
- 定义域
- 值域
- 奇偶性
- 单调性
- 取几个关键点
2025.01.15 函数的零点
零点的存在性定理
如果
y=f(x) 在
[a,b] 上图像是连续不断的,且
f(a)×f(b)<0,则
f(x) 在
(a,b) 中至少有
1 个零点。
- 例 1:
- 求证 f(x)=x3−2x+2 中至少有 1 个零点
- f(−2)=−2
- f(0)=2
- f(−2)×f(0)<0
- 所以 f(x)=x3−2x+2 中至少有 1 个零点。
今日份闲话:AK 必修一!
2025.05.06 指数函数
实数指数幂及其运算
- am(m<0)=a∣m∣1
- (am)n=(an)m=amn
- abm=ambm
- aman=am+n
- a2=9⟺a=±3
- a=b(a≥0,b≥0)
- x 读作 x 的算数平方根。
- na:
- 当 n 为偶数:a≥0。
- 当 n 为偶数:a∈R
- 当 na 有意义时:na=an1
例
1:求证:如果
a>b>0,
n 是大于
1 的自然数,那么
an1>bn1
- 假设 an1≤bn1,即 an1<bn1 或 an1=bn1。
- 根据不等式的性质与根式的性质,得 a<b 或 a=b。
- 与 a>b 矛盾。
- 因此假设不成立。
- 得证。
例
2:计算
393310:
- 393310=931(31031)=(32)31(35)31=332335=31=3
无理数作指数
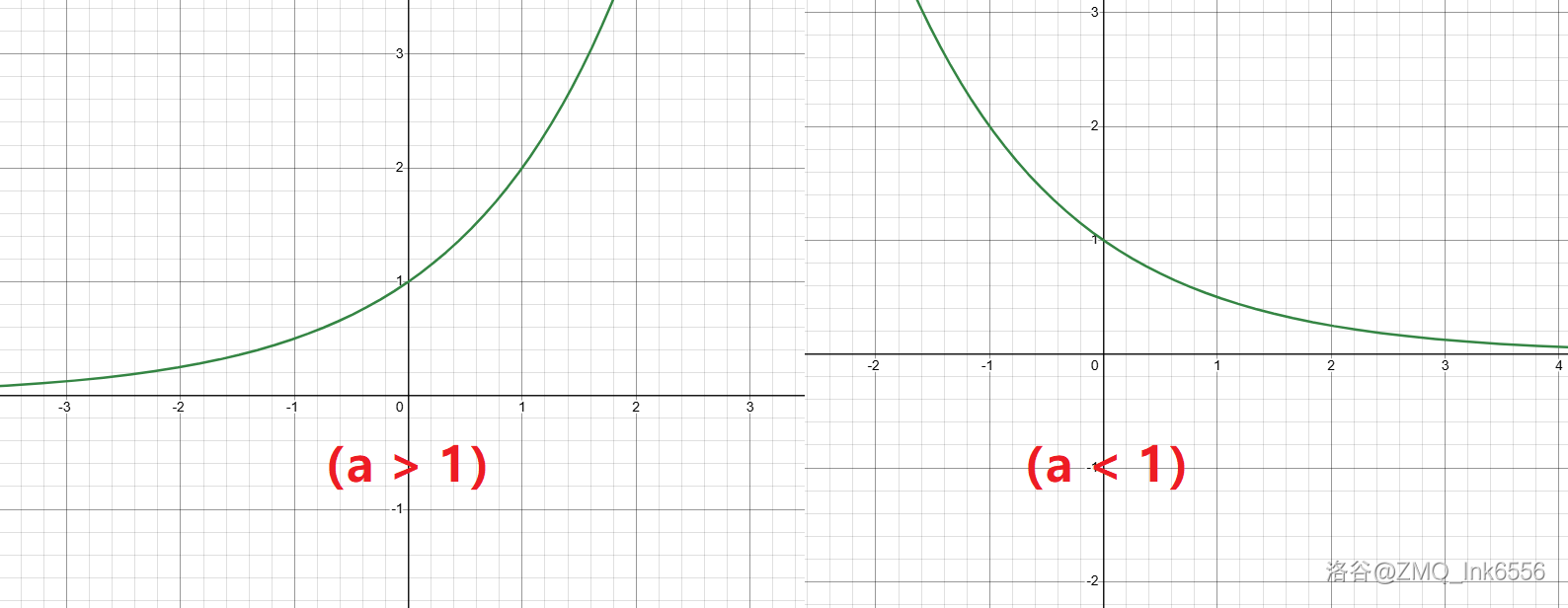
y=ax(a≥0 且 a=1)
- 定义域 (−∞,∞),值域 (0,∞)。
- a>1:递增。
- 0<a<1:递减。
- 必过 (0,1)。
- 0.8−0.1<0.8−0.2
- 2.5a<2.5a+1
例
2,已知
(73)a<(73)b,比较
6a 和
6b。
- a>b
- 6a>6b
2025.05.08 对数函数
对数
ab=N(a>0 且 a=1)
定义:
b 为以
a 为底
N 的对数,记为
b=logaN。
- 当 a=10 时:b=log10N=lgn(常用对数)。
- 当 a=e 时:b=logeN=lnN(自然对数)。
对数的运算
- loga(m×n)=logaM+logaN
- ab=N,b=logaN⟹ab=alogaN
- logaMb=blogaM
- logaNM=logam−logaN
- logab=logmalogmb
- logambn=mnlogab
对数函数
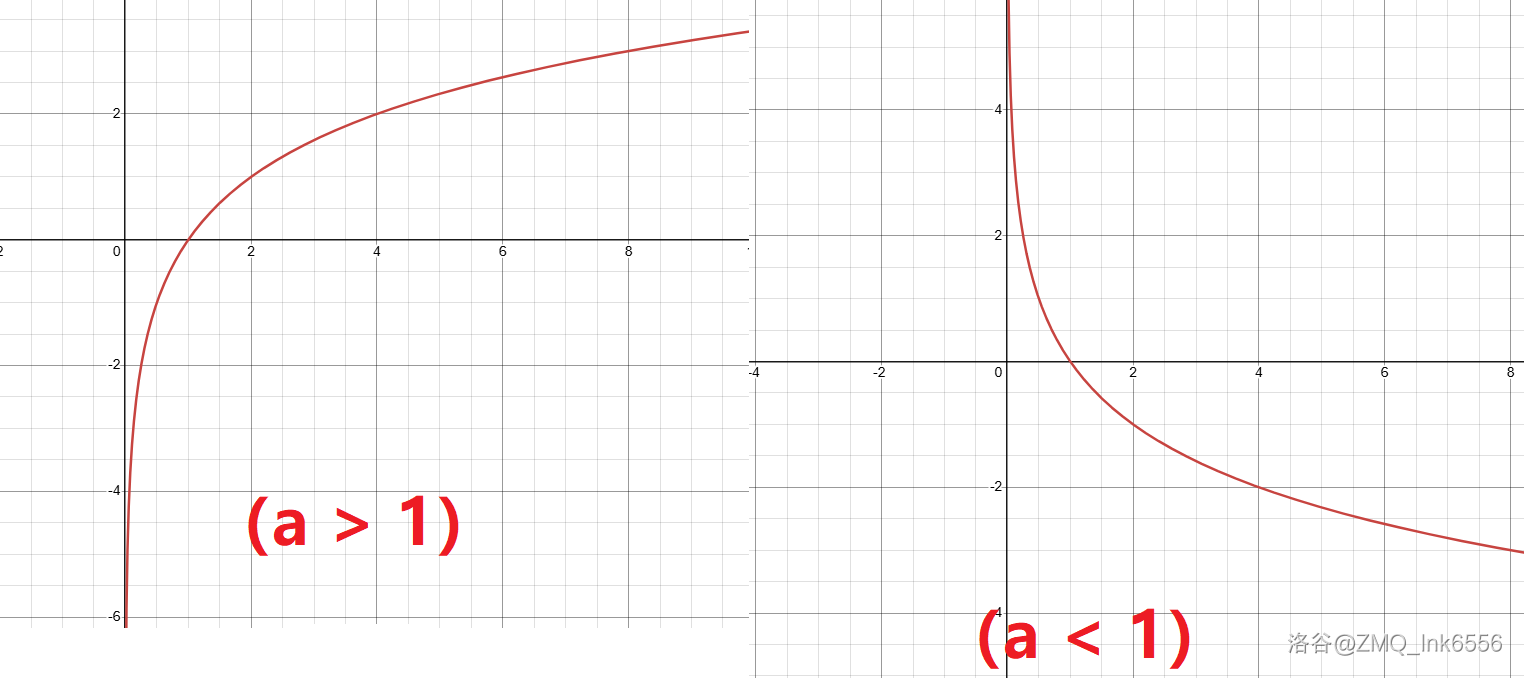
y=f(x)=logax(a>0 且 a=1)
- 定义域:(0,+∞)。
- 值域:(−∞,+∞)。
- 过定点:(1,0)。
- 单调性:
- a>1 时递增。
- 0<a<1 时递减。
2025.05.10 函数行性质
复合函数
- 内外层函数单调性一致:单调递增。
- 内外层函数单调性不一致:单调递减。
凹凸性
设
x1,x2∈R 且
x1=x2:
- 若 f(x1)+f(x2)>f(x1+x2) 则函数是凸函数。
- 若 f(x1)+f(x2)<f(x1+x2) 则函数是凹函数。
- 若 f(x1)+f(x2)=f(x1+x2) 则函数是一次函数。
- 运用在函数中的一段上同理。
单调性
已知
f(x) 为定义在
R 上的奇函数,且当
x>0 时,
f(x)=log21x。
- 例 1:求 x<0 时,f(x) 的解析式。
- 令 x<0,则 −x>0。
- 因为 f(x) 是奇函数。
- 所以 f(−x)=−log21(−x)。
- 求不等式 f(x)≤2 的解集。
- f(x)=log21x (0<x≤2) ∪ −log21(−x) (x<0)
- x>41 或 −4≤x<0。
20250520 幂函数
- y=kx2(抛物线)
- y=kx−1(反比例函数,双曲线)
20250520 平面向量及其线性运算
向量是什么
向量:
A B 或
a。
- 方向:A B 或 a。
- 长度:∣A B∣ 或 ∣a∣(一个向量的模)。
- 有方向的线段 = 矢量、位移、向量。
- 无方向的线段 = 标量、路程。
特殊向量:
0 和
0 有很大区别,但是
∣0∣=0。
方向相关
- 若向量 a,b 方向相同且长度相同,则 a=b。
- 若向量 a,b 方向相同或相反但是 a 的长度是 b 的 λ 倍,则 a=λb(若 λ 为正数则方向相同,若 λ 为负数则方向相反,若 λ=0 则 a=0)。
- 若 a 和 b 方向相同或相反,则 a 和 b 平行或共线。
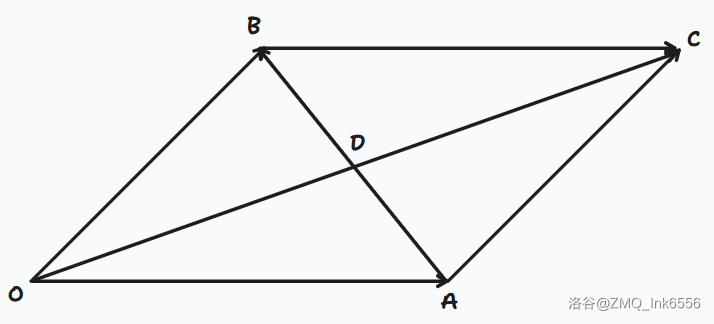
20250520 向量的加法
a b
若
A B 则
AB=a+b
AB+BC=AC
{∣AB∣+∣BC∣>AC(B 不在 AC 上)∣AB∣+∣BC∣=∣AC∣(B 在 AC 上)
所以 ∣AB∣+∣BC∣≥∣AC∣
向量减法
同一个起点的两个向量相减,指向被减数。
AB−AC=CB
向量乘法
3×a 的方向与
a 相同,长度是
3×∣a∣。
数乘运算: Δλa+μb
20250524 向量的基本定理与向量的坐标
共线向量的基本定理
- 满足 a=λb(b 为非 0,a//b),则 λ 唯一。
- 若 a=λb,且 λ=0,则 a 与 b 一定共线。
- 若 a 与 b 共线,且 b 为非 0,则 λ 唯一。
平面向量的基本定理
- x 轴单位向量:i
- y 轴单位向量:j
- 如果平面内两个向量 a 与 b 不共线,则对该平面内任意一个向量 c,存在唯一的实数对 (x,y),使得 c=xa+yb。
- 基底:{a,b}(不共线)。
- 基底 {a,b} 的分界式:c=xa+yb
例
1:已知
a 与
b 不共线,而且
a−xb 与
3a+2b 共线,求
x 的值。
- 因为 a 与 b 不共线,所以
2025.06.02 向量的坐标
OA=(x1,y1)
OB=(x2,y2)
∣OA∣=x12+y12
∣OB∣=x22+y22
表示
A 点坐标为
(x1,y1),
B 点坐标为
(x2,y2)。
中点坐标公式:
∣OD∣=(2x1+x2)2+(2y1+y2)2,
OD=(2x1+x2,2y1+y2)。
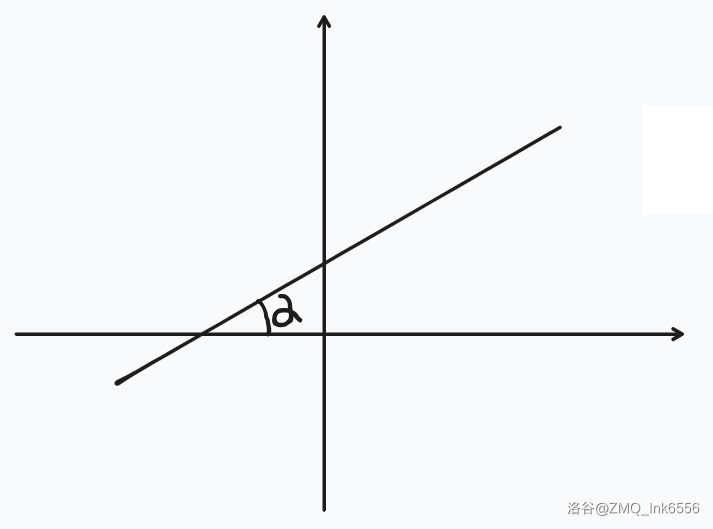
y=kx+b,k=tanα=cosαsinα
OA=(x1,y1)⟹k=x1y1
x1×y2=x2×y1⟺a 与
b 共线。
a⋅b=x1×x2+y1×y2=∣a∣×∣b∣cosα
cosθ=∣a∣×∣ba⋅b∣ 

![[pic]](https://cdn.luogu.com.cn/upload/image_hosting/plculgy1.png)