专栏文章
「烧情侣」
算法·理论参与者 57已保存评论 59
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 59 条
- 当前快照
- 1 份
- 快照标识符
- @mio2vsyo
- 此快照首次捕获于
- 2025/12/02 12:28 3 个月前
- 此快照最后确认于
- 2025/12/02 12:28 3 个月前
0 烧情侣
Problem 0(烧情侣) 给你一张 个点的无向图 ,初始时每个点上有无穷多对情侣。每一次操作你可以执行以下动作之一:
- 在任意顶点上放置一名团员,烧掉这个顶点上的所有情侣。
- 将一个团员从图中移除。
- 选择一个团员,将他移动到相邻的顶点上,并烧掉该顶点上的所有情侣。
每次操作后,情侣会以无限速度沿边占据所有可到达的顶点(情侣不可穿过团员)。问至少需要多少个团员,才能在有限次操作内烧掉所有情侣。
下面给出几个样例:
| 图类型 | 最小所需团员数 |
|---|---|
| 链 | |
| 环() | |
| 完全图() | |
| 菊花图() | |
| 网格图() |
本题由 @tiger0134 出于 6 年前,这里对问题描述略有修改。这篇博客以这道题目为线索,聊一聊图论中一些有趣的结论。
我尽量给出了一些核心定理的证明与算法代码实现,但不保证完全正确和严谨。欢迎与我讨论。
1 图搜索简介
在聊真正的烧情侣之前,我们先介绍一下 Search Games(图搜索问题),这在图论中被更广泛的研究,可以将其看成是“情侣在边上”的几种情况。稍后我们就介绍它们与 Problem 0 的相关性。
还是给你一张图 ,现在每条边上都有无穷多个情侣。我们的任务是通过调度团员,通过一系列操作“清理” (clear) 所有情侣。
这个任务的核心挑战在于一个严格的规则:重复污染 (Recontamination)。一条已经没有情侣的边,如果存在一条完全由未被团员守卫的点组成的路径,能通往任何一个仍被污染的区域,那么这条边会瞬间被再次污染。
我们的目标是在某个时刻,使图中所有边同时处于已清理状态。而我们最关心的问题是:要完成这个任务,最少需要多少名团员?这个最小值,就是图的搜索数 (search number)。
根据清理边的具体操作方式,我们定义了三种基本的游戏模型。
Problem 1.1(Edge Searching)这是最原始的图搜索游戏。
- 在任意顶点上放置一名新团员。
- 从任意顶点上移除一名团员。
- 将一名已在顶点上的团员沿一条边滑动到另一端。
Problem 1.2(Node Searching)Node searching 模型取消了“滑动”这一动态操作,规则更为静态。(注意:该模型中不存在“滑动”操作)
- 在任意顶点上放置一名新团员。
- 从任意顶点上移除一名团员。 (注意:该模型中不存在“滑动”操作)
Problem 1.3(Mixed Searching)Mixed searching 是上述两种模型的自然推广,它赋予了团员更大的策略自由度。
- 定义: 在 mixed searching 模型中,一条边 的清理方式十分灵活,可以是以下任意一种:
- 通过一名团员从 滑动到 (同 edge search)。
- 通过同时占据端点 和 (同 node search)。
- 基本操作:
- 在任意顶点上放置一名新团员。
- 从任意顶点上移除一名团员。
- 将一名已在顶点上的团员沿一条边滑动到另一端。
- Mixed search number: 该模型下的最小团员数量记为 。
为了确保你真的理解了上面三种图搜索的定义,可以看看下面图中的各个搜索数是不是和你算的一样:
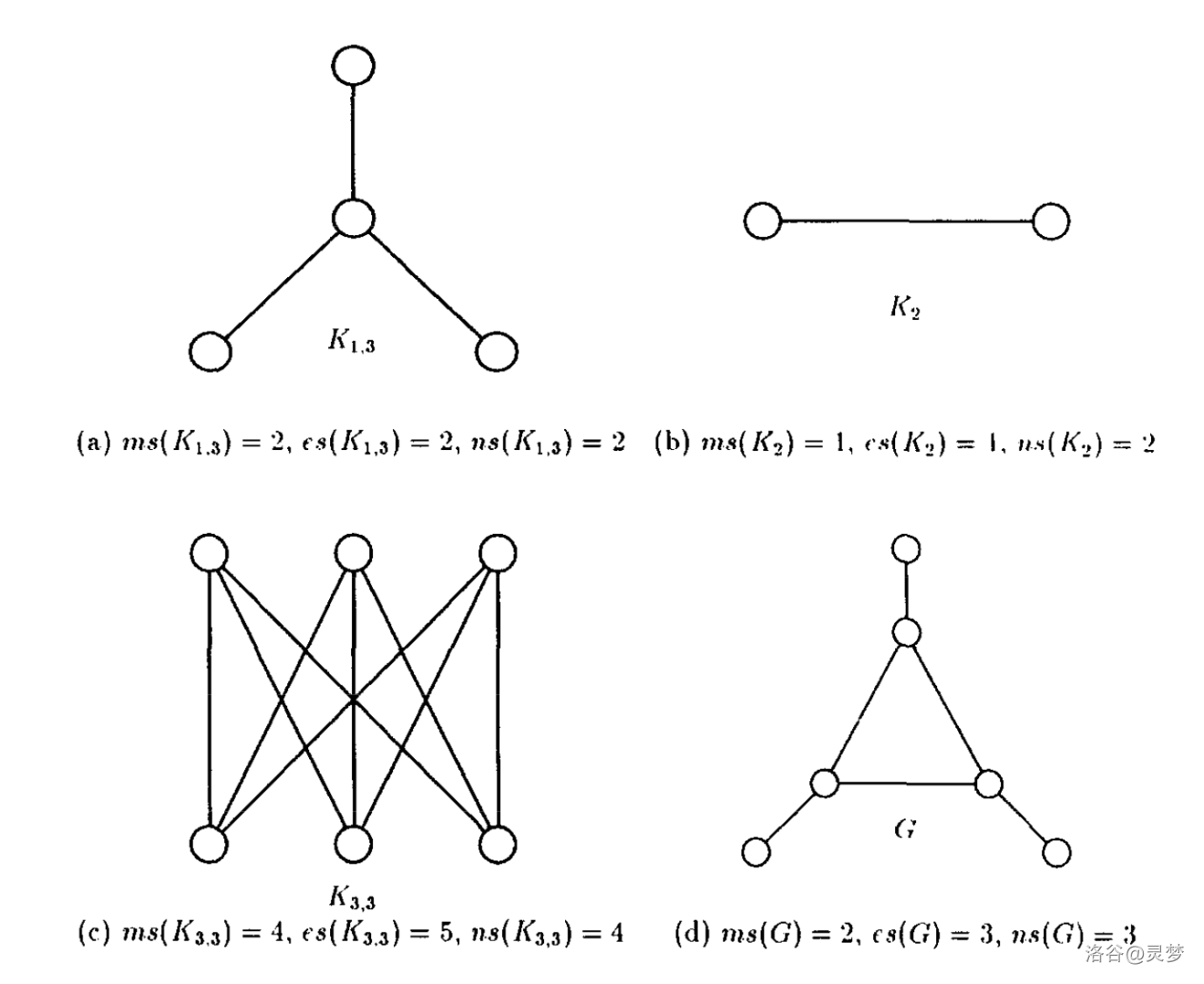
2. “烧”顶点与“烧”边的联系
在上一节中,我们定义了三种“烧边上的情侣”的战术:edge searching(依赖滑动)、node searching(依赖占位)和 mixed searching(全都要)。一个自然的问题是:这三种战术的优劣如何?它们的搜索数之间有什么样的数量关系?
由定义,任何一个合法的 edge search 或 node search 策略,本身就是一个合法的 mixed search 策略。因此,我们有 。这意味着,要完成任务,mixed search所需的团员数永远不会超过另外两种。
一个稍进一步的观察是,在 mixed search 的每一步中,我们都可以以最多一个额外团员为代价,通过 edge search 或 node search 来模拟。这给出了以下结论:
Proposition 2.1
这说明,三种搜索数之间的差距非常小,最多只相差 1。所有的 4 种情况都在上一节的图中被列出。
但是有时候我们期望的不是这种不等关系,而是等价关系,或者说一种零成本的模拟。所以我们的下一个问题是,三种搜索问题之间是否可以通过构造性的方法进行转化(规约)?
我们定义 和 分别是将无向图 的每条边替换成串联(in series)和并联(in parallel)的两条边后的图。那么有以下定理:
Theorem 2.2 且
Proof 这里只证 ,另一半也可以用类似的方法证明。
首先,显然有 ,因为对于 上的一个 edge search,放置和移除团员的操作都可以直接应用到 上;移动团员的操作对应 上连续沿串联边移动两次。结合 Proposition 2.1,我们有 。
对于另一个方向,我们分两步证明:
-
上的 edge search 可以转化到 上的 edge search。上的边 对应 上的两条边 和 。我们将所有的 收缩(contract),得到的新图 与 同构。 的每一个顶点 都是通过将 的一个顶点子集 合并而得到的。给定一个 的边搜索,我们通过以下规则将其转换为 的边搜索:如果在第 步,团员 位于顶点 ,那么在新的搜索的第 步,团员 就位于顶点 ,其中 。这满足了我们的要求。
-
上的 mixed search 可以转化到 上的 edge search。我们只要证明对于 上的一个 mixed search 方案,它所有通过同时占据两端点来清理的边,都可以在不增加新的团员的情况下,通过滑动操作来清理(回顾 mixed search 定义了两种清理方式)。具体来说,假设 mixed search 第 步有一条边 因为两个端点都被团员占据而被清理。由 的定义, 中至少有一个是二度点,不妨设 是二度点。那么我们在第 步之后插入连续第两步:先将 上的团员滑动到 ,再从 滑动到 。这样 就以滑动的方式被清理了,并且不会有任何边发生重污染。
因此对 上的任何一个使用 个团员的 mixed search 方案,我们都可以构造一个 上的使用 个团员的 edge search 方案。这意味着 。
Remark 2.3 Theorem 2.2 意味着 edge search 和 node search 可以规约到 mixed search 上,但反过来可能并不容易。从定义上来看,mixed search 拥有更强的搜索能力。
现在我们回来考虑 Problem 0,即情侣在点上的原版烧情侣问题。也许到这里你已经注意到,这个问题与 mixed-search 是等价的。
Theorem 2.4 “烧情侣”(Problem 0)在简单图 上的答案为 。
为了证明它,我们先证如下引理。
Lemma 2.5 对于简单图 上的一个搜索方案,在任何时刻,“烧情侣”被清理的点集为 当且仅当 mixed search 被清理的边集为 ,即 导出子图的边集。
Proof 假设在第 步,“烧情侣”被清理的点集为 ,那么 mixed search 被清理的边集为 。当第 步某个团员从 滑动到 后,我们将 清理 和 重污染 看成是依次发生的事件,并说明在这些事件中,引理保持成立。
-
清理:
- 如果 ,那么 和 都不会变化。
- 如果 ,考虑 的邻居 , 在第 步一定有团员驻留,否则 在第 步会被重污染。如果 那么 在 mixed search 中因滑动而清理;否则它因 和 同时被占据而清理。因此这一步后,,。
-
重污染:
- 如果“烧情侣”没有顶点可以被重污染,跳至 3。
- 否则,总可以选一个顶点 将要被重污染,且它有一个邻居 。这意味着 ,因此 mixed-search 中, 的所有邻边 都会被 重污染。,。重复 2。
-
此时“烧情侣”中已经没有顶点可以被重污染了。假设 mixed search 中还有边可以被重污染,那么总可以选一条边 将要被重污染,且 上没有团员,有一条邻边 。这意味着 ,因此 会被 重污染。这样导出了矛盾,所以此时 mixed search 中没有边可以被重污染。
这些事件结束后, 步中 “烧情侣” 和 mixed search 的所有操作完成,此时有 。容易证明,对于放置 / 移除团员的操作,该等式同样成立。由归纳法引理得证。
Proof of Theorem 2.4 由 Lemma 2.5 知,“烧情侣”清理完 当且仅当 mixed search 清理完 。因此“烧情侣”答案 当且仅当 mixed search 答案 。
Remark 2.6 注意 Theorem 2.4 在有重边的图上并不一定成立,比如 2 个点之间有 2 条边的图 ,烧情侣的答案为 1,而 。回顾证明过程,你会注意到有重边时“清理”这一步不一定保持 Lemma 2.5 成立。
3. 单调性(Monotonicity)
如果你花时间玩过一些样例的话,你可能会发现似乎总存在一种最优解(使用团员数最少的方案),可以在不发生重污染的情况下清理完所有情侣。我们称不发生重污染的方案为“单调”的。那么一个自然的问题是,是不是所有的搜索问题都存在单调最优解?
Definition 3.1(图搜索问题的单调性) 称一个图搜索问题具有单调性,如果对于所有图 ,存在一个搜索方案使用的团员数 ,则存在一个单调的搜索方案使用的团员数 。
不用多说就能感受到这个性质的重要性。如果它成立,一个搜索方案就可以用清理点(或者边)的线性长度序列来表示了。那么我们最关系的烧情侣问题,它具有单调性吗?似乎很符合直觉,但证明起来并不显然。在上一节中证明了前面定义的所有搜索问题都可以转化到 mixed searching 上,因此我们最好能直接证明 mixed searching 具有单调性。这一节我们就来证明它。
Theorem 3.2(Bienstock D, Seymour P. 1991) Mixed searching 具有单调性。
在开始之前,先来做一些记号与约定。
Notation 3.3
为什么要定义 crusade 呢?因为我们观察到,在描述 mixed search 方案时附带团员所在的点集有时显得有些冗余了。只有那些在 上的团员是有用的,拿掉其他的团员不会导致重污染。每次操作最多只会有一条边被清理,所以要限制 。
Proposition 3.4 如果 ,那么存在一个使用 个团员的 crusade。
Proof 我们证明对于任意一个使用 个团员的 mixed search 方案,都存在一个使用 个团员的 crusade。
假设 mixed search 方案为 ,且 。那么因为每个 ,所以 。因此 是一个使用 个团员的 crusade。
Remark 3.5 Proposition 3.4 的逆命题实际上是成立的,但证明并不显然。不过证明 crusade 的单调性是一件相对容易的事情。我们称一个 crusade 是 progressive 的,如果 ,且 。
Lemma 3.6 如果图 有一个使用 个团员的 crusade,那么也存在一个使用 个团员的 progressive crusade。
Proof 选择一个使用 个团员的 crusade ,使其满足:
(1) 最小,
(2) 在满足 (1) 的前提下, 最小。
我们将证明 是 progressive 的。任选一个 满足 。
(3) 。
因为 ,假设 (3) 不成立则 ,那么 将会是一个与 (1) 相矛盾的 crusade。
(4) 。
因为否则, 将会是一个与 (1) 相矛盾的 crusade。
(5) 。
因为根据 的次模性 (submodularity),我们有
由 (4) 可得, 。因此,
是一个使用 个团员的 crusade。由 (2),,于是该论断成立。
由 (3) 和 (5) 我们推断出 是 progressive 的。
Lemma 3.7 设 是一张图,每个点的度数都 。设 是一个使用 个团员的 progressive crusade,并且对于 ,。那么存在一个单调的 mixed search,它使用 个团员,并且确保 的边按 的顺序被清理。
Proof 我们归纳地构造这个 mixed search。
假设对于 ,我们已经成功地按顺序清理了边 ,并且没有清理任何其他的边。令 。可以肯定的是, 中的每一个顶点当前都被一个团员占据,因为它同时与一条已清理的边和一条被污染的边相关联。移除所有其他的团员(不会发生重复污染)。由于 ,它的端点都不在 中。令 为 的端点集合。
-
如果 ,我们可以将新的团员放置在 的端点上,并宣告它被清理。
-
我们接下来假设 。那么(1) 。如果 ,那么 ,这与假设矛盾。(2) 。这是因为对于任意 , 度数 ,它除了 之外还与至少一条不在 中的边 关联,且 。(3) 。如果 ,那么由 (2) 有 ,则 ,这与假设矛盾。由 (3),选择一个顶点 。那么 ,并且 有端点 ,且 除了 之外,不与任何在 中的边(即有情侣的边)相关联。因此,我们可以通过将位于 的团员沿着 滑动到 来清理 ,而不会发生重污染。
下面我们将前面几个命题和引理拼装起来,证明 mixed searching 的单调性。
Proof for Theorem 3.2 不妨假设 没有孤立点。令 是对 每个点加上自环得到的图,这样 中的点度数就 。有一个明显的观察是, 上的 mixed search 可以自然地导出一个 上的 mixed search(试用定义证明),因此 。由 Proposition 3.4 知, 上存在一个使用 个团员的 crusade。由 Lemma 3.6, 上存在一个使用 个团员的 progressive crusade。由 Lemma 3.7 知, 上存在一个使用 个团员的单调的 mixed search,这也给出了 上的一个单调的 mixed search。
Corollary 3.8 烧情侣问题具有单调性。
这可以由 Lemma 2.5 和 Theorem 3.2 推出。
Remark 3.9 使用 Theorem 3.2 结合类似 Theorem 2.4 的证明方法,也可以得出 edge searching 和 node searching 具有单调性。这是 mixed search 灵活性的体现,其他问题的单调性都可以归约到它上面。
4. 一般图上的 算法和树上的 算法
这一节讨论的都是 Problem 0(烧情侣)的算法。
单调性带给我们的一个直接的好处是,可以暴力枚举顶点被清理的顺序。容易得到一个基于动态规划的 算法。严谨起见,下面给出转移方程的正确性证明。
Theorem 4.1 记用单调方案清理点集 需要的最小团员数为 ,则
其中 。
Proof 考虑枚举 是 中最后一个被清理的点,那么这种情况下清理 需要的团员数要么是 ,要么是 。
注意 可以看成是 的“边界点”的集合,清理 后需要用团员占据这些点来保证不被重污染。不难发现下面事实成立:
其中 是 中 的邻居。我们分下面几种情况讨论:
-
- 如果 ,那么说明清理完 后,团员数比边界点数多,此时可以将空闲的团员移到 上来清理。
- 如果 ,那么 。取 ,将点 上的团员滑动到 上来清理。
这样没有新增团员,因此用 来更新 。 -
此时 ,且 。这意味着清理完 后所有团员都在边界点上(没有空闲的团员),且没有与 相邻的团员。因此只能用 来更新 。
综上可得此时应该用 来更新 。
考虑到既然是题解,最好附上代码,下面给出这个算法的 C++ 实现。
Algorithm 4.2(一般图上的 算法)
CPP#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 20;
int N[MAXN]; // N[i] 表示 i 的邻居集合 mask
int f[1 << MAXN]; // f[S] 表示清理点集 S 需要的最小团员数
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
N[u] |= 1 << v;
N[v] |= 1 << u;
}
f[0] = 0; // 初值
for (int S = 1; S < (1 << n); S++) {
f[S] = n;
// 计算边界点集合 partial(S)
int partial = 0;
for (int v = 0; v < n; v++)
if (S & (1 << v) && (S & N[v]) != N[v])
partial |= 1 << v;
// 状态转移
for (int v = 0; v < n; v++)
if (S & (1 << v))
f[S] = min(f[S], max(f[S ^ (1 << v)], __builtin_popcount(partial & ~(1 << v)) + 1));
}
cout << f[(1 << n) - 1] << std::endl; // 输出答案
}
现在我们来讨论树上的烧情侣问题,目标是找出一个快速的多项式复杂度算法。为了方便,仍用 表示树 上的烧情侣问题的答案。
总体的思路是树形 DP,但在仅拥有单调性的情况下,设计一个能够快速合并子树的好的状态并不容易。实际上,我几年前在洛谷社区上写了一个比较 Trivial 的状态和转移,后来发现是错的。下面我们从一个关键性质(Theorem 4.4)的观察入手,给出一个正确、高效且巧妙的 DP 算法。
Lemma 4.3 设 是一棵树, 是一个正整数。假设对于 中的任意顶点 ,子图 最多只有两个 的连通分量,并且没有任何连通分量的 。那么,。
Proof 设 就是树 ,并设 是一个顶点,使得 拥有最大数量的 的连通分量。
如果 没有任何 的连通分量,那么 。
如果 有两个 的连通分量,我们令 是其中一个连通分量,并令 是在 中与 相邻的顶点。我们递归地定义 和 (),其中 是 的一个 的连通分量,并且 是在 中与 相邻的顶点。我们这样定义直到 不再有 的连通分量。令 为 的另一个 的连通分量,并令 是在 中与 相邻的顶点。我们再如上所述递归地定义 和 ()。注意,对于 , 最多只有一个 的连通分量,否则 将会有三个或更多 的连通分量,这与 Lemma 4.3 的假设相矛盾。
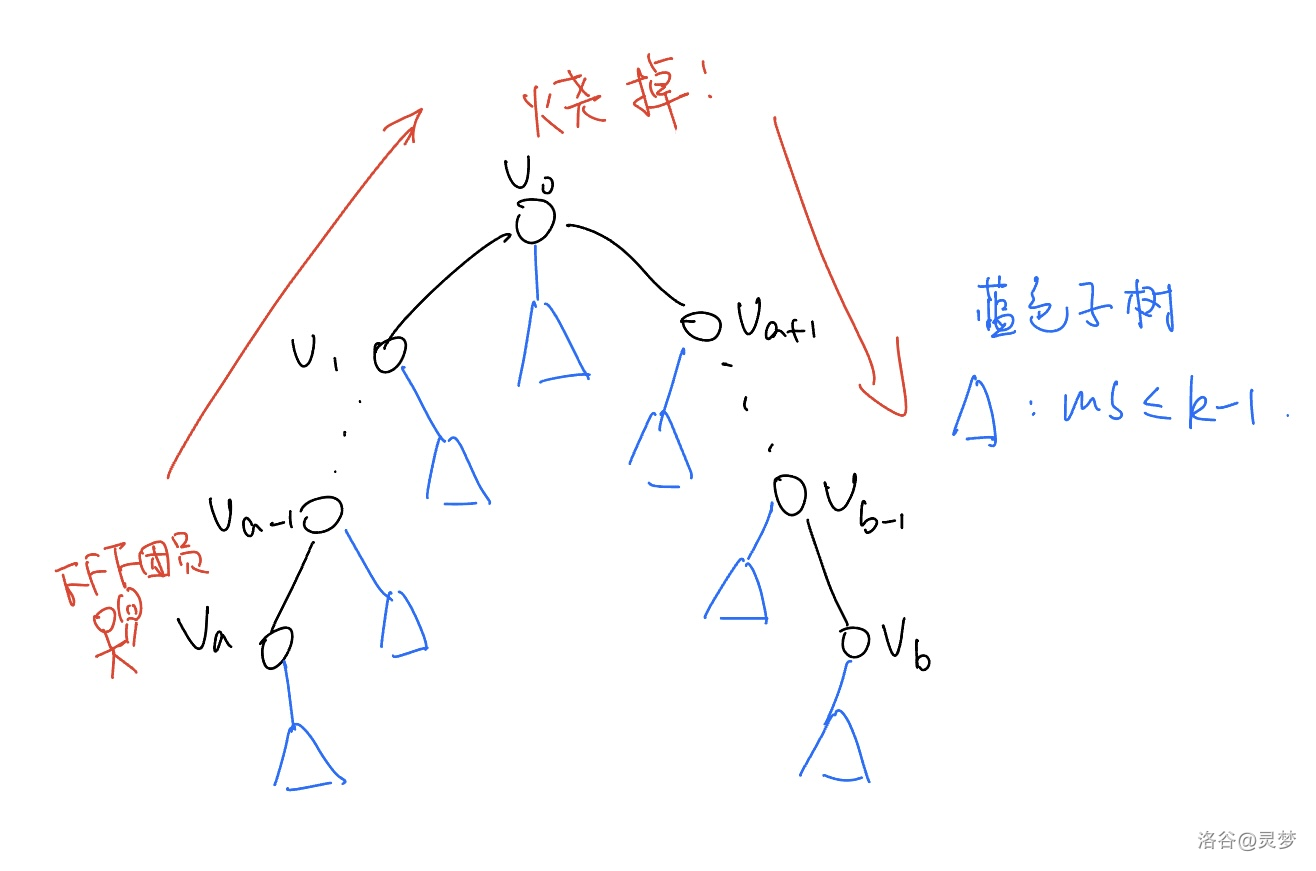
此时这棵树长成如图所示的样子,我们可以用 个团员沿着 走过去,顺便烧掉 的子树中的情侣,因此 。
如果 只有一个 的连通分量,情况也是类似的。
Theorem 4.4 对于任意树 和正整数 , 当且仅当 中存在节点 使得 至少有三个连通分量的 。
Proof (⇒) 设 。令 是满足 的一棵 的极小子图。因为 是极小的,所以对于任意 , 中没有 的连通分量。因此,存在一个顶点 使得 至少有三个 的连通分量,否则由 Lemma 4.3 可得 ,矛盾。
(⇐)设 中存在一个顶点 使得 至少有三个 的连通分量。记 是这样的三个连通分量,假设有一个使用 个团员清理 的单调方案,使得 依次被完全清理。那么在清理 的某一刻,所有 个团员都在 内部,这样 中的情侣就会重污染已经清理的 ,矛盾。因此 。
Corollary 4.5 对于任意树 ,。
这可以由 Theorem 4.4 归纳得到。
Theorem 4.6(Takahashi et al. 1995) 对于任意树 , 可以在线性时间内求出。
Proof 我们首先介绍路径向量(path vector),也就是树形 DP 的状态设计。
我们为任何以顶点 为根的树 定义路径向量 来计算 。 描述了 的答案。 和 描述了 的状况如下:如果存在一个 ,使得 有两个答案为 且不包含 的连通分量,那么 ,且 是 中包含 的那个连通分量的路径向量;否则, 是 中答案为 的连通分量的数量,且 。值得注意的是,对于任何顶点 , 中答案为 的连通分量数量至多为两个(根据 Theorem 4.4)。另请注意,如果存在这样一个 ,使得 有两个答案为 且不包含 的连通分量,那么这个 是唯一确定的。如果没有这样的 ,那么 中答案为 且不包含 的连通分量数量,不会超过 中答案为 的连通分量的数量。在下文中,我们将 中的元素 表示为 ,其中 是 、 或 。
感性地讲,为什么要去维护路径向量呢?从 Theorem 4.4 可以看出, 并不好通过简单地合并得到,它有一个“临界效应”:当某个节点连接了三个或更多“复杂”的分支时,整个结构的复杂度会突然“升级”,当前子树的答案 。我们关心的是,合并一棵新的子树时,是否会导致临界效应。
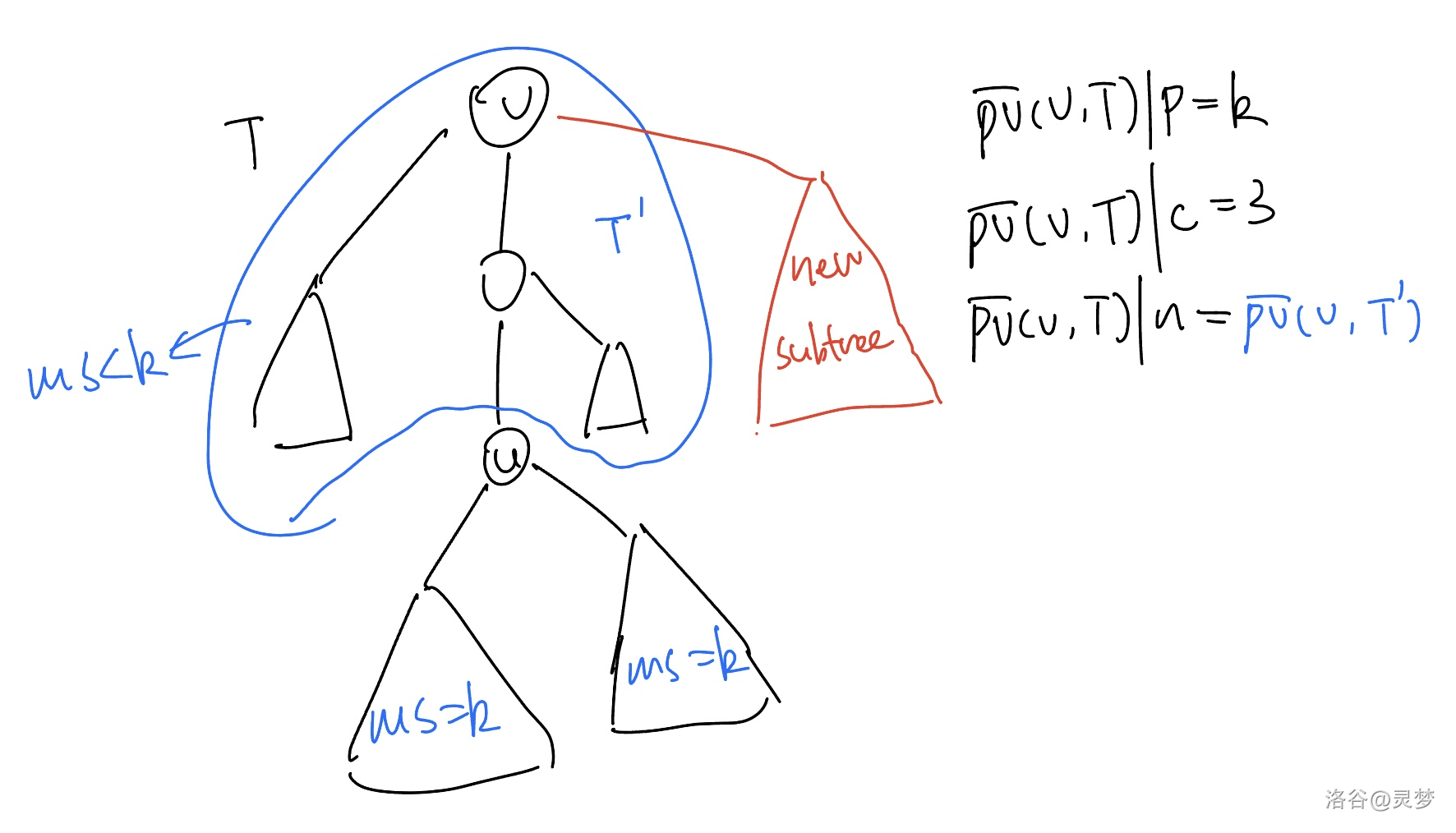
当 时,需要再合并 棵答案为 的子树导致当前子树的答案 ;当 时,情况会转化为 包含 的连通分量 与新子树的合并(如图所示),这可能会导致递归合并。所以我们在 的路径向量中记录了 ,指向 的路径向量;而 也有可能指向某个更小的连通分量 的路径向量(如果 ),这给出了一个路径向量的链结构。下面我们形式化地定义路径向量链。
设 是一棵以 为根的树, 是 的路径向量 。当 时,我们递归地定义 和 如下:设 是这样一个顶点,使得 有两个不包含 且答案为 的连通分量, 是以 为根的 的连通分量,而 是 的路径向量 。我们称这样的路径向量 为路径向量 的 链 。我们在 的链中定义 、、 和 如下:定义 ;定义 ,如果 或 ,其中 是满足 的最大整数;定义 ,如果 被定义且 ;定义 。因此,我们将一个路径向量扩展为 。在程序中,我们省略了对路径向量中 和 的替换描述,因为不会引起混淆。此外,在替换之后,我们可以在常数时间内更新链中路径向量的 和 。因此我们也省略了对这些操作的描述。为简单起见,如果对 的替换使用了 ,我们将其缩写为 。
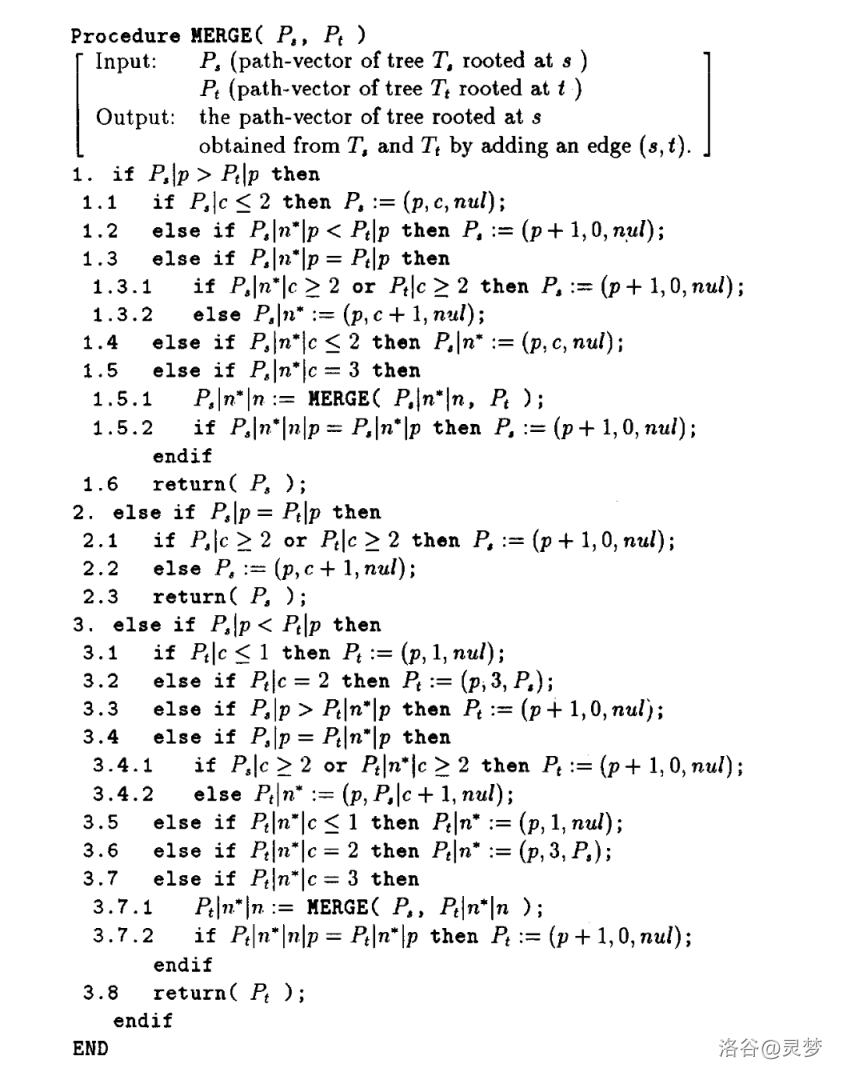
假设一棵以 为根的树 是由一棵以 为根的树 和一棵以 为根的树 通过添加一条边 得到的。基于 Theorem 4.4,图中所示的
MERGE 过程根据 的路径向量 和 的路径向量 ,在 时间内递归地计算 的路径向量,其中 。注意,除了递归调用外,MERGE 过程的时间复杂度是 。由于每当 MERGE 过程被递归调用时,两个合并树中较大的 值至少减少 2,因此递归调用的次数最多为 。根据 Corollary 4.5,使用 MERGE 过程合并路径向量直接 DP 的时间复杂度是 。
在图中所示的
LMERGE 过程中,我们可以通过使用路径向量链中的 和 在 时间内确定 ,其中 。如果在 LMERGE 过程的 1.2 或 2.2 处确定了 ,那么 MERGE 过程的递归调用次数最多为 ;否则,MERGE 过程在 时间内返回路径向量 。因此,LMERGE 过程在 时间内计算两个子树连接后的路径向量 。图中所示的 DFS 过程通过使用 LMERGE 过程,根据以 的子节点为根的最大子树的路径向量,计算出以 为根的最大子树的路径向量。 MAIN 过程通过 DFS 过程获得的 的路径向量,得到 的 值。该算法从通过删除 中所有边得到的孤立顶点开始,通过逐条添加边来重构 ,同时计算连通分量的路径向量。令 表示计算 的路径向量所需的时间, 表示通过
LMERGE 过程从 和 的路径向量获得 的路径向量所需的时间。根据 Corollary 4.5,我们有以下结论:注意到由 和对于 的
所定义的递推关系满足 。验证这一点的一个简单方法是通过直接归纳法证明对于 , 。因此,我们可以证明该算法的时间复杂度为 ,其中 。
Algorithm 4.7(树上的 算法)
CPP#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int MAXN = 1000005;
struct PathVector {
int p;
int c;
PathVector *n;
PathVector *b;
PathVector *n_star;
PathVector *b_star;
PathVector *btm;
PathVector(): p(1), c(0), n(nullptr), b(nullptr), n_star(this), b_star(this), btm(this) {}
void set(int p, int c, PathVector *n = nullptr, PathVector *s = nullptr) {
this->p = p;
this->c = c;
this->n = n;
if (!s) s = this;
if (n) {
n->b = this;
if (this->p == n->p + 1) {
this->b_star->n_star = n->n_star;
n->n_star->b_star = this->b_star;
} else {
this->b_star->n_star = this;
}
s->btm = n->btm;
} else {
this->b_star->n_star = this;
s->btm = this;
}
}
};
vector<int> G[MAXN]; // 邻接表
vector<PathVector*> pv_mem;
PathVector* merge(PathVector* P_s, PathVector* P_t) {
if (P_s->p > P_t->p) {
PathVector* P_sn = P_s->n_star;
if (P_s->c <= 2) P_s->set(P_s->p, P_s->c);
else if (P_sn->p < P_t->p) P_s->set(P_s->p + 1, 0);
else if (P_sn->p == P_t->p) {
if (P_sn->c >= 2 || P_t->c >= 2) P_s->set(P_s->p + 1, 0);
else P_sn->set(P_sn->p, P_sn->c + 1, nullptr, P_s);
} else if (P_sn->c <= 2) P_sn->set(P_sn->p, P_sn->c, nullptr, P_s);
else if (P_sn->c == 3) {
P_sn->set(P_sn->p, P_sn->c, merge(P_sn->n, P_t), P_s);
if (P_sn->n->p == P_sn->p) P_s->set(P_s->p + 1, 0);
}
return P_s;
} else if (P_s->p == P_t->p) {
if (P_s->c >= 2 || P_t->c >= 2) P_s->set(P_s->p + 1, 0);
else P_s->set(P_s->p, P_s->c + 1);
return P_s;
} else { // if P_s->p < P_t->p
PathVector* P_tn = P_t->n_star;
if (P_t->c <= 1) P_t->set(P_t->p, 1);
else if (P_t->c == 2) P_t->set(P_t->p, 3, P_s);
else if (P_s->p > P_tn->p) P_t->set(P_t->p + 1, 0);
else if (P_s->p == P_tn->p) {
if (P_s->c >= 2 || P_tn->c >= 2) P_t->set(P_t->p + 1, 0);
else P_tn->set(P_tn->p, P_s->c + 1, nullptr, P_t);
} else if (P_tn->c <= 1) P_tn->set(P_tn->p, 1, nullptr, P_t);
else if (P_tn->c == 2) P_tn->set(P_tn->p, 3, P_s, P_t);
else if (P_tn->c == 3) {
P_tn->set(P_tn->p, P_tn->c, merge(P_s, P_tn->n), P_t);
if (P_tn->n->p == P_tn->p) P_t->set(P_t->p + 1, 0);
}
return P_t;
}
}
PathVector* lmerge(PathVector* P_s, PathVector* P_t) {
if (P_s->p > P_t->p && P_s->c == 3) {
PathVector* P_prime = P_s->btm->b_star;
while (P_prime->p < P_t->p) P_prime = P_prime->b->b_star;
if (P_prime == P_s) P_s = merge(P_s, P_t);
else P_prime->b->set(P_prime->b->p, P_prime->b->c, merge(P_prime, P_t), P_s);
return P_s;
}
if (P_s->p < P_t->p && P_t->c == 3) {
PathVector* P_prime = P_t->btm->b_star;
while (P_prime->p < P_s->p) P_prime = P_prime->b->b_star;
if (P_prime == P_t) P_t = merge(P_s, P_t);
else P_prime->b->set(P_prime->b->p, P_prime->b->c, merge(P_s, P_prime), P_t);
return P_t;
}
return merge(P_s, P_t);
}
PathVector* DFS(int u, int f) {
PathVector* P_u = new PathVector();
pv_mem.push_back(P_u);
for (int v: G[u]) if (v != f) {
PathVector* P_v = DFS(v, u);
P_u = lmerge(P_u, P_v);
}
std::cout << "DFS(" << u << ") = " << P_u->p << std::endl;
return P_u;
}
int main() {
std::ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
cout << DFS(1, 0)->p << endl;
for (auto ptr: pv_mem) delete ptr;
pv_mem.clear();
return 0;
}
5. NP-Completeness
上一节中我们给出了一般图上的指数时间算法,以及树上的线性算法。那么对于一般图,我们有可能找到一个多项式时间算法吗?
很遗憾,事情并没有那么简单。这一节我们要证明,对于一般图,烧情侣问题是 NP-Complete 的。也就是说,如果你能找到这个问题的一个多项式时间解,那么所有 NP 问题都可以在多项式时间内求解,P = NP 就得证了。这看起来就很困难!
首先由第 3 节证明的单调性可知,所有的图搜索问题(包括烧情侣)都是 NP 问题,因为只要给出清理边(或者点)的顺序,容易在多项式时间内验证一个解。所以我们只需要证明烧情侣问题是 NP-hard 的,而证明方法是将一个已知的 NP-hard 问题 多项式时间归约 到烧情侣。归约的路径自然有很多,我们这里采用 Megiddo 等人 [3] 的方法,证明 Edge Searching 是 NP-hard 的。由于第 2 节中已证明 Edge Searching 可以归约到 Mixed Searching(Theorem 2.2),而 Mixed Searching 等价于烧情侣(Theorem 2.4),所以烧情侣也是 NP-hard 的。
Theorem 5.1(Megiddo et al. 1988) Edge Searching 是 NP-Complete 的。
我们通过将一个已知的 NP-complete 问题——等规模子集最小割 (MIN-CUT INTO EQUAL-SIZED SUBSETS)——归约到 Edge Searching 问题来证明其 NP-hardness。
Problem 5.2(等规模子集最小割)
- 问题: MIN-CUT INTO EQUAL-SIZED SUBSETS
- 实例: 一个图 ,其中 是偶数,以及一个正整数 。
- 提问: 是否存在一个将 划分为两个子集 和 的方案,使得 ,并且连接 和 的边的数量(即 )不超过 ?
这是一个 NP-Complete 问题,但它的证明细节并不在我们的讨论范围内。感兴趣的同学可以参考 [5](P. 210 [ND17]),网上可以找到 PDF 版本。
下面为定理的证明引入核心工具:关于搜索完全图(Clique)的引理。证明的构造依赖于完全图 极难被搜索的特性。
Lemma 5.3 假设在搜索 () 的过程中,在某个步骤 ,第一个顶点关联的所有边被完全清理。那么在该步骤中,必然有至少 个团员位于 上。
Proof 要想让一个顶点 的所有边都被清理,意味着它的所有 个邻居都必须被“守卫”或者连接它们的边刚刚被清理。具体来说,假设最后一条被清理的边是 。此时,为了防止重复污染,在 的另外 个邻居上必须都驻留着守卫。同时,清理边 本身也需要至少一个团员(从 滑动到 )。因此,总共需要 个团员。
Lemma 5.4 假设图 包含 个顶点不相交的 副本。那么在搜索 的过程中,对于任意 (),必然存在一个时间点,此时有 个团(clique)中至少有一个已清理的顶点,而另外 个团则完全没有,并且这 个团中的某一个,包含 个或更多的团员。
Proof 这是 Lemma 5.3 的直接推论。由于清理任何一个团的“启动成本”极高,在任何一个步骤中,最多只能“攻破”一个新的团。这为清理过程建立了一个自然的先后顺序。
Lemma 5.5 假设图 包含多个顶点不相交的 副本。在搜索的某个时刻,设 是一组已开始清理的团,而 是一组完全未被清理的团。如果 是 的一条边,其中 属于 中的一个团, 属于 中的一个团,那么 或 上必须有一个团员。
Proof 这条边 正是已清理区域和污染区域的边界。为了防止重复污染,这条边界必须被守卫。如果边 本身已清理,那么 必须被守卫,以防止污染从 蔓延过来。如果边 本身被污染,那么 必须被守卫,以防止污染通过 蔓延到 的已清理部分。
回到定理的证明。
Proof of Theorem 5.1 从 MIN-CUT 实例 出发,构造 Edge Searching 实例 :
-
参数设定: 设原图 有 个顶点,最大度为 。选择两个巨大的整数 和 。
-
构造新图 H:
- (i) 对于 中的每个顶点 ,在 中创建一个包含 个顶点的完全图(团),记为 。
- (ii) 额外创建一个“特殊的”-团,记为 。
- (iii) 在任意两个团 和 (,包括 )之间添加 条边,此外在这些团之间添加额外边:
- 如果 是 中的一条边,则在团 和 之间再添加 3 条边。
- 对于任意 ,在特殊团 和普通团 之间再添加 条边。
其中 (iii) 中加边的方式要保证每个团中的顶点关联至多一条到其他团的边。这一点是可以做到的,因为 。 -
构造目标搜索数 s:
接下来我们证明 当且仅当 有一个大小不超过 的等规模割。
方向一 (⇒): 如果 有一个好解,那么 可以用 个团员完成搜索。
假设 存在一个大小为 的等规模割 。
-
搜索策略: 按照顺序清理:先清理所有 对应的团,然后清理特殊团 ,最后清理所有 对应的团。
-
普通团: 清理普通团 时,需要的团员数最多为
-
特殊团: 团员数量在清理特殊团 时达到峰值。此时,我们需要:
- 个团员来清理 内部。
- 守卫连接 中 个团和 中 个团的边。根据 Lemma 5.5,这需要 个团员。
- 守卫连接 和 之间由割边诱导的额外边。割的大小为 ,每条原边对应3条新边,需要 个团员。
总共需要 个团员。因为 ,这个数量不超过我们设定的 。
方向二 (⇐): 如果 可以用 个搜索者完成搜索,那么 有一个好解。
-
根据 Lemma 5.4,在搜索过程中,必然有一个时刻,恰好有 个普通团已开始清理,而另外 个普通团完全未动。并且在此时,有一个团正被“攻破”(即上面有 个团员)。
-
这个被“攻破”的团必须是特殊团 。为什么?如果被攻破的是一个普通团 ,由 Lemma 5.5 可知,需要的团员数最少为矛盾。这个迫使任何最优策略都必须选择 作为“中转站”。
-
构造割: 在 被攻破的那个时刻,让 是那些已开始清理的团对应的原图顶点集, 是未清理的团对应的顶点集。我们自然地得到了一个等规模划分 。
-
计算割的大小: 在这一刻,总共 个团员被分配到:
- 上至少有 个。
- 守卫 和 之间连接的边,至少需要 个。
- 剩下的预算用于守卫 和 之间由割边诱导的额外边。
- 从总预算 中减去固定开销:。这意味着用于守卫割边的预算最多为 。
- 由于每条原图中的割边对应 中的 3 条边,所以原图割的大小最多是 。
综上所述我们已经证明了,当且仅当 中存在一个大小不超过 的等规模割时, 才能用 个团员完成搜索。由于这个归约是多项式时间的,我们证明了 Edge Searching 是 NP-hard 的。结合 Remark 3.9 可知,Edge Searching 是 NP-complete 的。
Corollary 5.6 烧情侣问题是 NP-Complete 的。
Proof 由 Corollary 3.8 知烧情侣是 NP 问题。由 Theorem 2.2 和 Theorem 2.4 可知,Edge Searching 可以归约到烧情侣问题,因此烧情侣问题也是 NP-Complete 的。
6. 从搜索游戏到图的内在结构
在前面的章节中,我们已经对“烧情侣”这个看似简单的游戏有了深入的了解。我们不仅定义了它的三种战术变体——edge, node, 和 mixed searching——还通过一个巧妙的归约,证明了计算最优策略(即 )是一个NP-hard问题。
这一节中,我们将从动态的搜索游戏(主要是 mixed searching,即“烧情侣”)出发,寻找它与图的静态内在结构之间的对偶关系。
Definition 6.1 (Pathwidth, pw) 一个图 的路径分解 (path-decomposition) 是一个由顶点子集组成的序列 ,满足:
- 对于所有不同的 ,都有 ;
- ;
- 对任意边 ,存在某个 使得 ;
- 对所有 满足 ,都有 。
路径分解的宽度是 。图 的路径宽度 ,是其所有可能的路径分解中的最小宽度。
Definition 6.2 (Proper-Path-Width, ppw) 一个路径分解 被称为适度 (proper) 的,如果它满足
- 对所有 满足 ,都有 。 图 的适度路径宽度 ,是其所有可能的适度路径分解中的最小宽度。
Notation 6.3
- 称一个宽度为 的 (proper-)path-decomposition 为 -(proper-)path-decomposition。
- 称一个 -(proper-)path-decomposition 为满(full)的,如果 且 。
下图展示了图 的一个 path-decomposition,proper-path-decomposition 和 full proper-path-decomposition。
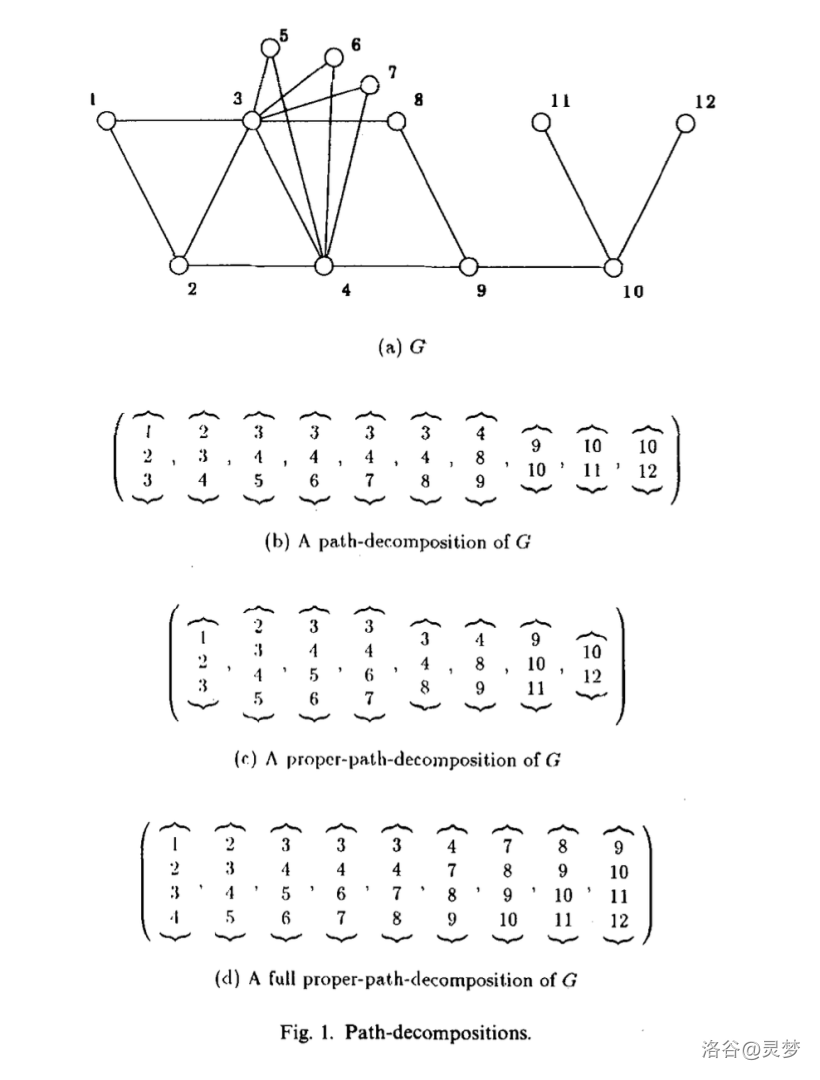
Takahashi 等人的工作揭示了 Mixed Searching 与 Proper-Path-Width 之间令人惊叹的等价关系。我们先给出三个引理,其中第二个引理的技术性比较强,篇幅所限不给出完整证明。
Lemma 6.4 (1) 满足 Definition 6.1 中的条件 4 当且仅当 中的每个顶点出现在连续的 中。(2) 一个 path-decomposition 是 proper 的(即满足 Definition 6.2 中的条件 5)当且仅当 。
这个引理是基于定义的一些简单推导。
Lemma 6.5 如果一个图 有一个 -path-decomposition 满足:那么 就有一个 full -proper-path-decomposition。
证明的大致思路是,选择满足 的路径分解中 最小的 ,通过反证法证明它满足 和 ,然后由 Lemma 6.4(2) 可知它是 proper 的。完整证明可以参考原论文 [1]。
Lemma 6.6 如果图 满足 ,那么 有一个 full -proper-path-decomposition。
这是 Lemma 6.5 的直接推论。 说明 有一个 -proper-path-decomposition,它满足 条件,由 Lemma 6.5 可以得到 的一个 full -proper-path-decomposition。
Theorem 6.7 对于任意简单图 ,。
Proof 首先证明 。
假设 ,由 Lemma 6.6 知可以找一个 的 full k-proper-path-decomposition 。
如果 ,那么令 和 是 中两个不同的顶点,我们将 个团员放置在 的顶点上。如果 ,则将 上的团员滑动到 并放置在 上。否则,从 删除一个团员,并在 上放置一个团员。这定义了一个使用 个团员的 mixed search。因此,我们假设 。我们可以通过以下步骤获得一个使用 个团员的 mixed search:
-
Step 1: 令 是 中的一个顶点。将 个团员放置在 的顶点上。
-
Step 2: 令 是 中的一个顶点。如果 ,将 上的团员朝向 滑动并放置在 上。否则,从 删除一个团员并在 上放置一个团员。令 。
-
Step 3: 当 时,重复执行步骤3。令 。令 是 中的一个顶点,令 是 中的一个顶点。如果 ,将 上的团员朝向 滑动并放置在 上。否则,从 删除一个团员并在 上放置一个团员。
-
Step 4: 令 是 中的一个顶点,令 是 中的一个顶点。如果 ,将 上的团员朝向 滑动并放置在 上。否则,从 删除一个团员并在 上放置一个团员。
根据 full k-proper-path-decomposition 的定义,顶点 () 和 () 都是唯一确定的。值得注意的是,对于 ,有 ,并且 。
一条两个端点都在 () 中的边会被清理,因为在步骤1、2或3中, 的顶点上同时都有团员。同样,一条两个端点都在 中的边也会被清理,因为在步骤4中, 的顶点上同时都有团员。由于 是简单图,最多只有一条边连接 和 (),并且这条边 (如果存在的话)是通过滑动一个团员来清理的。因此,所有边都至少被清理了一次。
假设连接 中顶点的所有边都已清理,并且 个团员被放置在 的顶点上。由于 ,当一个团员从 上被删除或滑走时,所有与 相关联的边(除了可能存在的 )都已经被清理了。因此,当团员被放置在 上时, 中的所有边都处于已清理状态,并且 个团员被放置在 的顶点上。通过归纳法,没有边会发生重复污染。
因此,上述过程确实是一个使用了至多 个团员的 mixed search,我们有 。
接下来证明 。
假设我们有一个使用 个团员的 mixed search 。对于 的第 个操作,我们如下定义顶点集 :
(1) 当一个团员被放置在(或从)一个顶点上删除时,我们将 定义为当前拥有团员的顶点集合。
(2) 当一个团员从 滑动到 时,我们将 定义为由 以及当前拥有团员的其他顶点组成的集合。
令 是由此产生的顶点集序列。由于在第 个操作中被清理的边的两个端点都包含在 中,所以所有边都包含在某个 中。由于 是简单的, 并且 的每个顶点都出现在连续的 中。根据 的定义,对于任意 ,都有 。
令 是 的一个最大子序列,使得对于任意不同的 ,都有 。注意, 满足 Definition 6.1 中的条件 (i)-(iv)。我们将证明,这个 k-路径分解 满足 Lemma 6.5 中的条件 (*)。
如果 中有一个是由规则(1)定义的,那么很容易看出 。如果 都是由规则(2)定义的,那么 ,并且在 中存在两个不同的顶点 和 ,使得 且 。因此,我们有 。
所以, 满足 Lemma 6.5 中的条件(*),并且根据 Lemma 6.5,存在一个 的 full k-proper-path-decomposition。因此,。
这个深刻的联系并非孤例。事实上,更早的研究已经揭示了 Node Searching 与标准路径宽度之间的关系。
Theorem 6.8 (Kirousis & Papadimitriou, 1986; Möhring, 1990) 对于任意图 ,。
还有一些其他与搜索数 / path-width 等价的问题,例如:
Problem 6.9 我们称图 的一个线性布局(linear layout)是 到 的一个排列 ,定义 。 关于 的顶点分离数(vertex separation)为 。图 的顶点分离数 。
Theorem 6.10(Kinnersley, 1992) 对于任意图 ,。
Definition 6.11 图 的一个 k-clique 是 的一个有 个顶点的完全子图。对于正整数 ,我们递归地定义 k-tree:
- 个顶点的完全图是 k-tree
- 给定一个 个点的 k-tree (),新增一个与 中某个 k-clique 相邻节点得到的 个节点的图是 k-tree。 一棵 k-tree 一条 k-path,如果 ,或者 恰好有两个 度点。 我们称 k-path 的子图为 partial k-path。
Remark 6.12 1-path 是链;1-tree 是树。
Theorem 6.13 (Takahashi et al., 1995) 对于任意正整数 ,一个简单图 的 当且仅当 是一个 partial k-path。
(⇒) 假设 。根据 Lemma 6.6,存在一个 的 full h-proper-path-decomposition 。如果 ,那么 是一个在 个顶点上的完全图的子图,因此我们得出 是一个 partial h-path。因此,我们假设 。我们根据 按如下方式构造一个 h-path :
- 令 是 中的一个顶点。定义 为在顶点集 上的 h-完全图。
- 定义 是通过将顶点 以及连接 和 中所有顶点的边加入到 中而得到的 h-path。
- 给定 (),定义 是通过将顶点 以及连接 和 中所有顶点的边加入到 中而得到的 h-path。
- 定义 。
由定义可以验证 是一个 h-path。此外,根据 proper-path-decomposition 和 的定义,我们有 并且 。因此, 是一个 partial h-path,所以它也是一个 partial k-path。
(⇐) 反过来,不妨假设 是一个有 () 个顶点的 partial h-path (),并且 是一个满足 和 的 h-path。因为从一个 h-path 中删除一个度为 的顶点(如果存在的话)得到的图仍然是一个 h-path,所以 可以通过如下方式获得:
- 记 为一个在 个顶点上的完全图。
- 给定 和 ():记 是通过加入一个不在 中的顶点 并连接 和 中所有顶点而得到的 h-path,并令 是 中包含 的一个 h-clique。
- 定义 。
我们定义 () 和 。容易验证 是 h-path-decomposition,用 Lemma 6.4 可知 是 的一个 full h-proper-path-decomposition。
因此,我们有 。
根据 -path 的定义,一个 个节点的 -path 有不超过 条边。因此有如下推论
Corollary 6.14 对于任意正整数 ,如果一个简单图 的 ,则 。
7. Treewidth 有界图的线性算法
在第 5 章中,我们证明了烧情侣问题在一般图上是 NP-hard 的;第 4 章给出了树上的一个线性算法。这种树上可以做但图上做不了的问题其实很常见。现在的问题是,这个问题还在哪些图类上有多项式算法?
一个自然的想法就是,如果一个图长得很像树,那么我们也许可以用类似树上的算法来解决。比如在基环树上的题可以拆成环上的多棵树来求解,仙人掌上的题可以考虑用它圆方树求解。这一节我们来讨论一个相对先进的方法,可以某种意义上定量地衡量一个图有多“像”一棵树;对于那些很像树的图,提出一个烧情侣问题的快速算法。
上一节最后讨论了 k-path 与 k-tree,Theorem 6.13 告诉我们 partial k-path 就是 的图族。那么我们可不可以类似地讨论 partial k-tree,也就是 k-tree 的子图?
Definition 7.1 图 的一个树分解(tree decomposition)是一个二元组 ,其中 且 是一棵以 为顶点集的树,满足
- ;
- 对任意边 ,存在某个 使得 ;
- 对所有 ,如果 在 上 和 之间的路径上,则 。
树分解的宽度是 。图 的 treewidth 是所有可能的树分解的宽度中的最小值,记作 。
这里定义的 treewidth 就是我们用来衡量一个图有多“像”一棵树的量,同时类似 Theorem 6.11 也可以证明图 的 当且仅当 是一个 partial k-tree。
我们的思路是,对于 treewidth 有界的图,先求出它的树分解,然后在分解树上 DP 来解决烧情侣问题。而求一个 partial k-tree 的树分解是一个被广泛研究的问题,经过学术界一段时间的研究和改进,下面是一个里程碑式的工作。
Theorem 7.2(Bodlaender H L. 1993) 存在复杂度 的算法,要么求出图 宽度 的 tree decomposition,要么报告 。
这意味着如果 是常数,可以在线性时间内求出一个 partial k-tree 的树分解。但直接在一般的树分解上操作比较复杂,所以需要一些技巧。
我们定义一个树分解 是好(nice)的,如果 可以看成一棵有根二叉树,且
- 如果一个节点 有两个儿子 ,则 ;
- 如果一个节点 只有一个儿子 ,则 与 恰有差一个元素( 比 多或者少一个元素)。
Lemma 7.3 如果图 满足 ,则有一个宽度为 的好树分解。此外,当给定一个图 的树宽为 的树分解时,我们可以在线性时间内构造出一个该图 的树宽为 的好树分解。
这个构造好树分解的算法就像用若干两个插座的插排来接用电器。如果原树分解的节点 有不少于两个儿子,就在构造的树中添加若干有两个儿子的“中继节点”,直到有足够的中继节点用来接上原树分解的节点 的所有儿子。
现在考虑一个好树分解 。对 ,记 , 为 的导出子图。
如果 有一个子节点 ,那么 是通过向 添加一个顶点 获得的(在这种情况下, 的邻居必须属于 ),或者 和 是相等的(在这种情况下,)。如果 有两个子节点 和 ,那么 是通过取 和 的不交并集,然后并上 中的顶点得到的。
定义一张 -边界图 (boundary graph) 是标记了 个顶点的图,形式上可以表示为二元组 ,其中 是一个图,,且 。那么,如果找到了图 的一个宽度为 的好树分解, 可以通过对 -边界图的一系列操作序列来构建。
- 起始 (Start):给定一个 -边界图 ,其中 。
- 遗忘 (Forget):给定一个 -边界图 ,取一个顶点 ,然后得到 -边界图 。
- 引入 (Introduce):给定一个 -边界图 ,其中 ,取一个顶点 ,一个子集 ,然后得到 -边界图 。
- 连接 (Join):给定两个 -边界图 ,,其中 ,取 。
Theorem 7.4 存在线性时间算法,可以判定一个 partial k-tree 是否满足 。
由于博主写这篇文章时间有限,暂时无法给出这个定理的完整证明和实现代码 TAT,这里只说一下算法的大致思路(比较感性)。有机会我会补全这一部分。感兴趣的同学可以参考 [7],介绍的是一个求 pathwidth 的算法。
设 是一个 partial k-tree,由 Theorem 7.2 和 Lemma 7.3 可以在线性时间内求出一个 的宽度为 的好的树分解 。和前面一样定义 和 ,我们要对每个 维护一些“部分解”,然后支持 Start Forget Introduce Join 四种操作的快速更新。这里的“部分解”就是 的 proper k-path decomposition。
我们先对 Join 操作进行分析。如果 有一个 proper k-path decomposition ,那么不难证明 和 去掉空集和相等的集合后分别是 和 的 proper k-path decomposition。也就是说,如果我们对每个 都维护了所有 proper k-path decomposition,那么就可以在 Join 操作完成信息合并。但这样显然开销太大。但是聪明的你会发现,很多信息是冗余的,因为被合并的点集只有 ,其中 。我们只关心 是什么,而不关心 这部分具体长什么样子,合并的时候只需要知道 即可。
所以我们只维护 proper k-path decomposition 的特征。对于 的 proper k-path decomposition ,它的特征为二元组 。Join 操作合并两个特征 与 时,要求 与 去掉连续重复元素后相等,否则它们不可能是一个大的 proper k-path decomposition 分裂出来的两个分解的特征。如果满足这一点,则通过添加重复元素的方法,让它们长度相同(均为 ),然后新的特征为 ,其中 ,。你要用定义检查新的特征是否确实可以是 proper k-path decomposition 的特征。
Forget 和 Introduce 操作都要比 Join 操作简单,而 Start 操作可以在与 有关的时间内暴力枚举所有 proper k-path decomposition 来求出特征集。每次个操作会带来的新特征数都是与 有关的常数,因此这是一个线性算法。
Theorem 7.5 在 partial k-tree 上( 为常数),烧情侣问题有线性算法。
之前我们证明过对于简单图,烧情侣的答案等于 proper-path-width。我们可以直接枚举 来运行 Theorem 7.4 中的判定算法!实际上,partial 2-tree 就是广义串并联图,我们可以在线性时间内求解广义串并联图上的烧情侣问题。
这种应对 treewidth 有界的图,在树分解上 DP 是一种构造算法的范式,最大独立集 / 最小斯坦纳树等经典的 NPC 问题都可以在线性时间内解决。
8. 参考文献
[1] Takahashi A, Ueno S, Kajitani Y. Mixed searching and proper-path-width[J]. Theoretical Computer Science, 1995, 137(2): 253-268.
[2] Bienstock D, Seymour P. Monotonicity in graph searching[J]. Journal of Algorithms, 1991, 12(2): 239-245.
[3] Megiddo N, Hakimi S L, Garey M R, et al. The complexity of searching a graph[J]. Journal of the ACM (JACM), 1988, 35(1): 18-44.
[4] Takahashi A, Ueno S, Kajitani Y. Minimal acyclic forbidden minors for the family of graphs with bounded path-width[J]. Discrete Mathematics, 1994, 127(1-3): 293-304.
[5] DS G M R J. Computers and intractability: a guide to the theory of NP-completeness[J]. San Franciso WH Freeman and co, 1979.
[6] Kinnersley N G. The vertex separation number of a graph equals its path-width[J]. Information Processing Letters, 1992, 42(6): 345-350.
[7] Bodlaender H L, Kloks T. Better algorithms for the pathwidth and treewidth of graphs[C]//International Colloquium on Automata, Languages, and Programming. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991: 544-555.
[8] Bodlaender H L. A linear time algorithm for finding tree-decompositions of small treewidth[C]//Proceedings of the twenty-fifth annual ACM symposium on Theory of computing. 1993: 226-234.
相关推荐
评论
共 59 条评论,欢迎与作者交流。
正在加载评论...