专栏文章

P4528 [CTSC2008] 图腾 题解

UUKBwyx
P4528题解参与者 8已保存评论 12

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
12 条
当前快照
1 份
快照标识符
@minl4t72
此快照首次捕获于
2025/12/02 04:11
3 个月前
此快照最后确认于
2025/12/02 04:11
3 个月前
查看原文
来一个比较优雅的做法。
约定在 yy 轴上红点和其他点间的相对高度是重要的，黑点和黑点间的相对高度是不重要的，在 xx 轴上任意两点的相对位置都是重要的。
首先考虑这种怎么数。
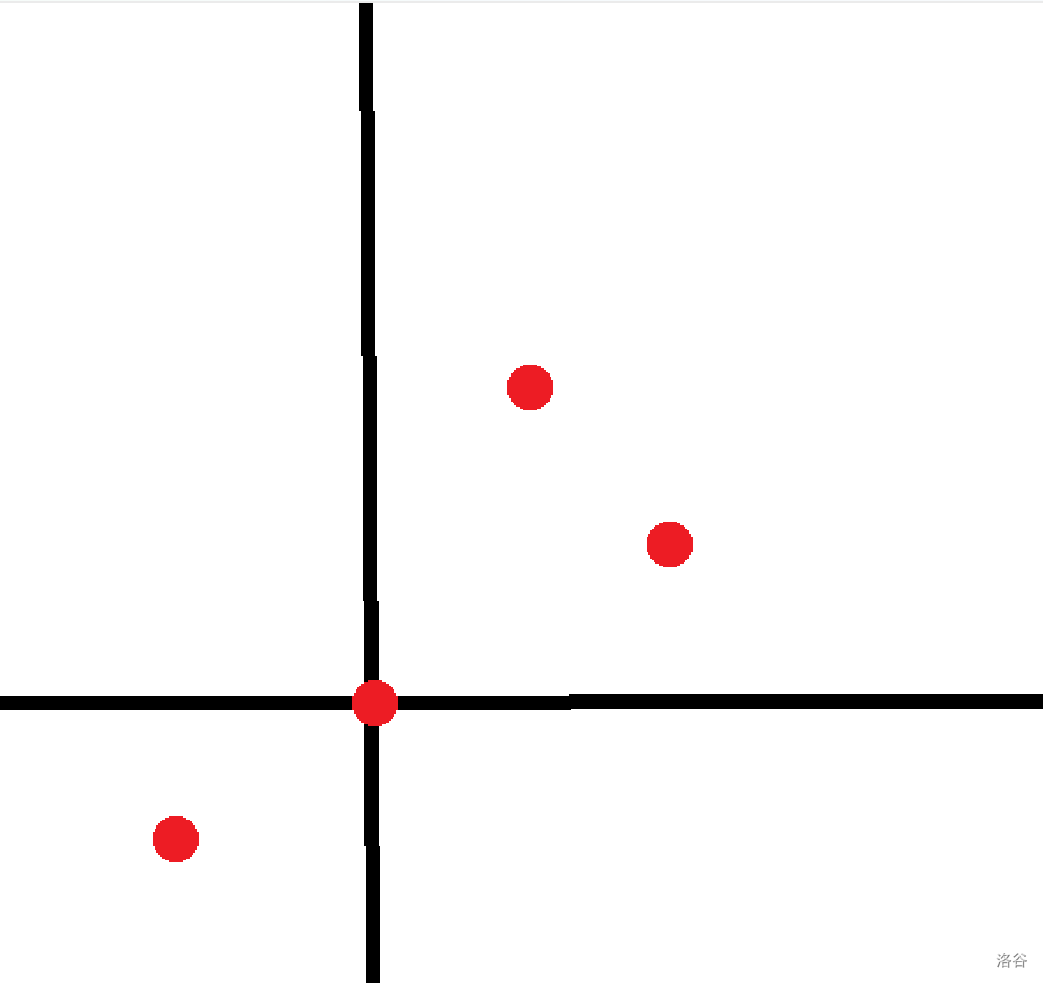
这个可以用这种情况：
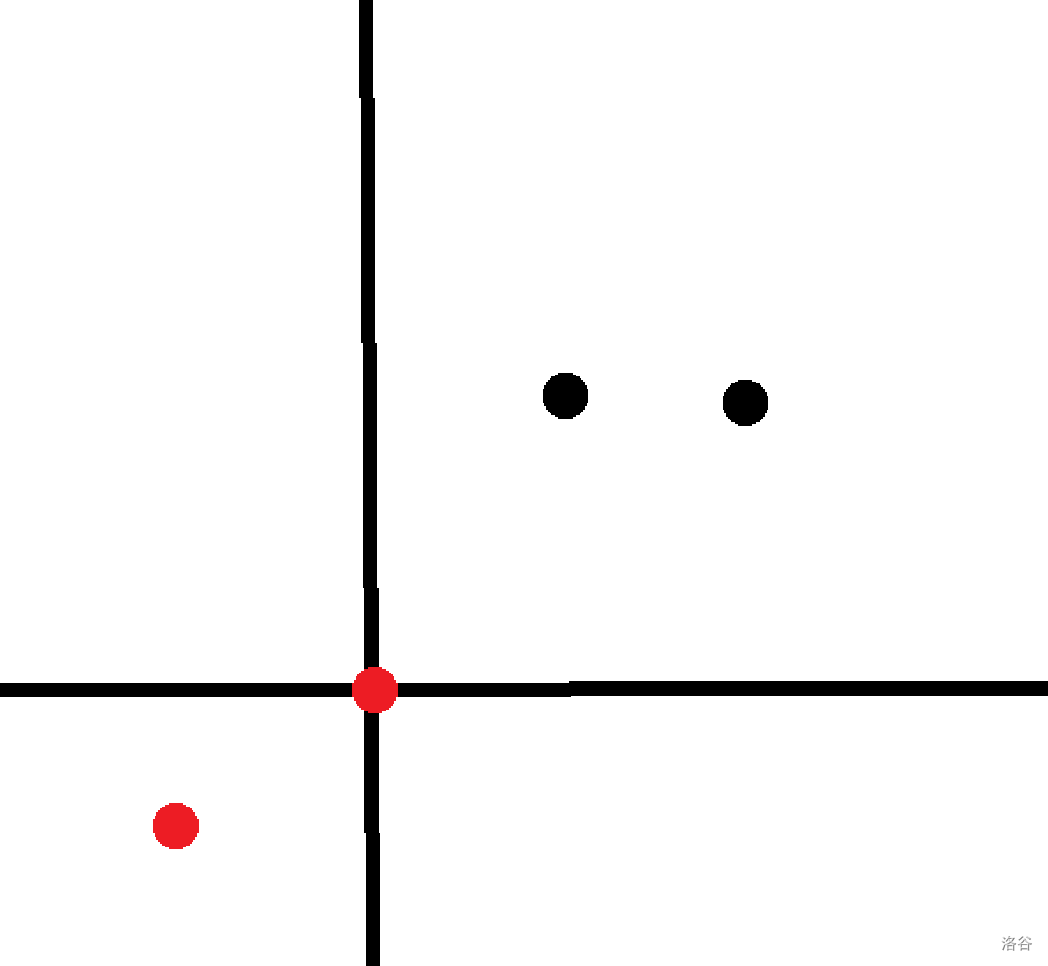
减掉这种情况得到。
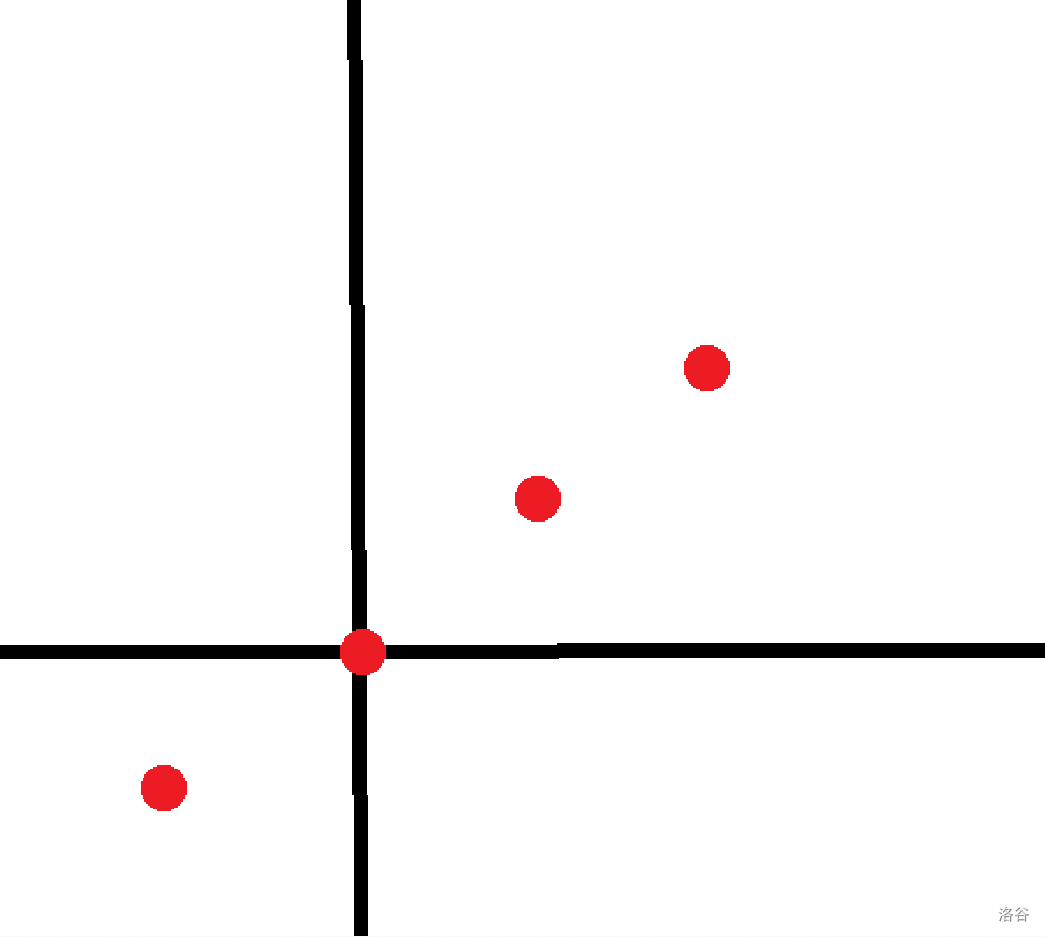
然后观察剩下的两个，它们分别长这样：
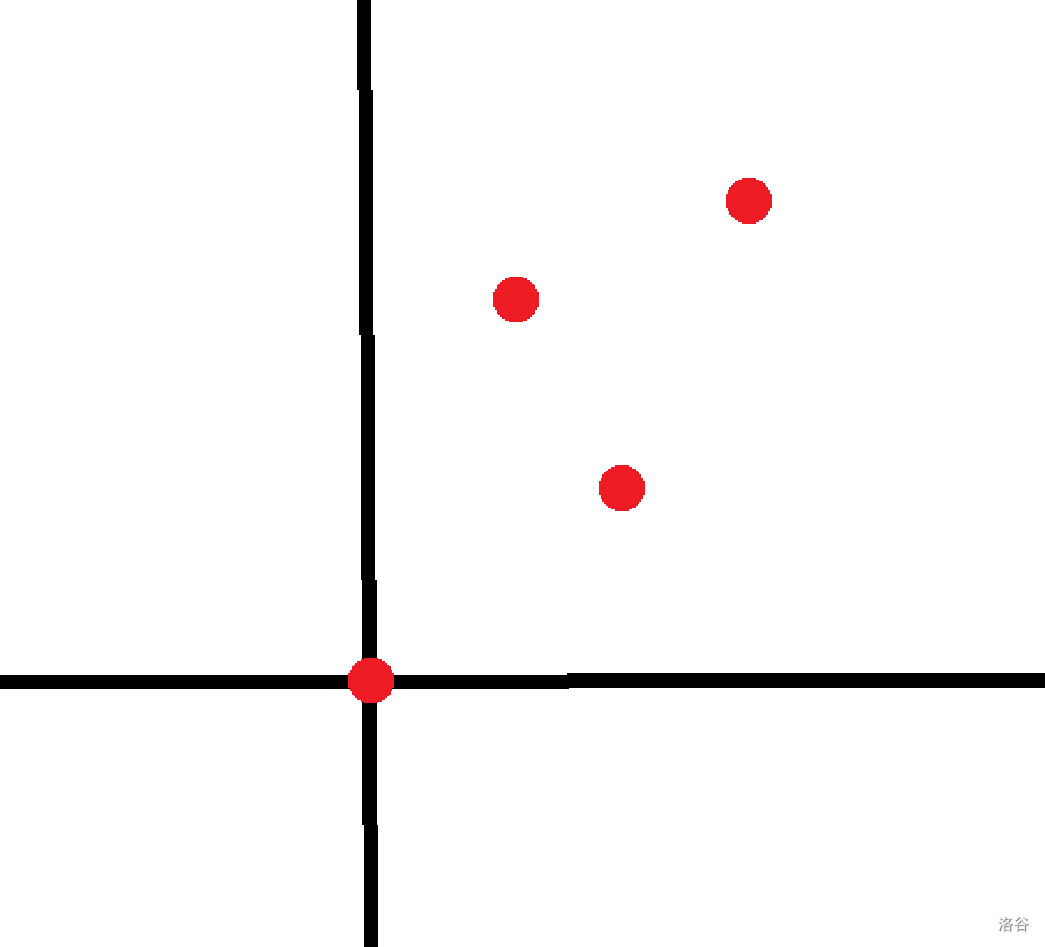
这种每出现一个答案 +1+1。
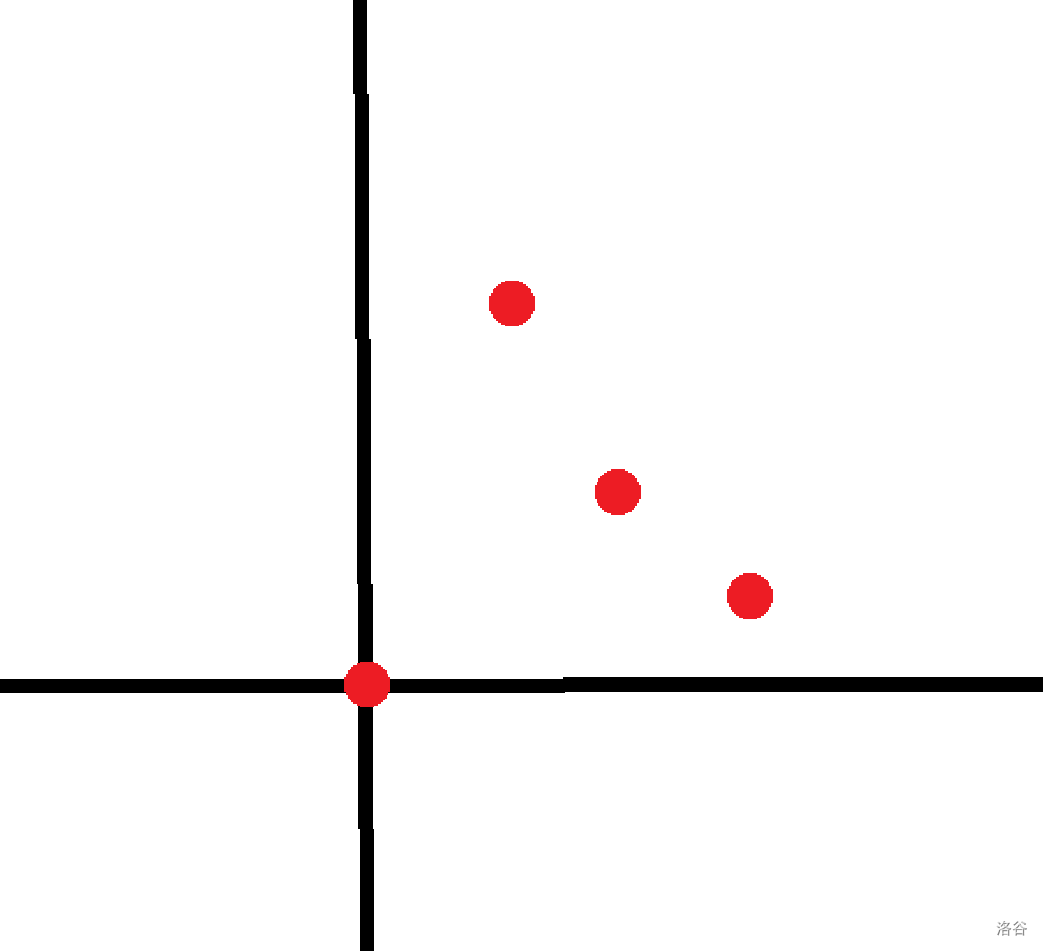
这种每出现一个答案 −1-1。
观察发现这两种的区别在于第 44 个点的高度。
这启发我们把四排列计数换成三排列计数。
也就是，把四个点的贡献拆到三个点上。
对于这种情况：
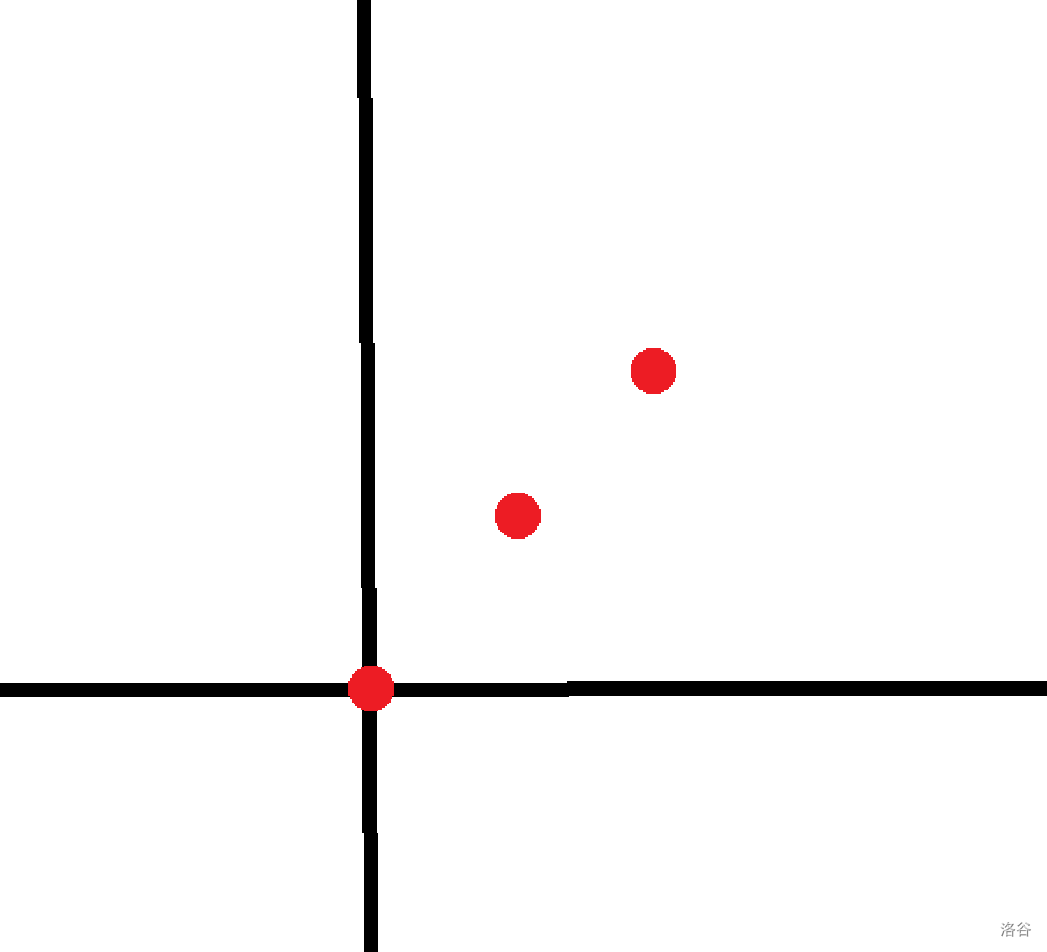
只要它的剩下一个点在第一个点右上方并且不与这两个红点重复，就直接把答案 +1+1。
而对于另一种情况：
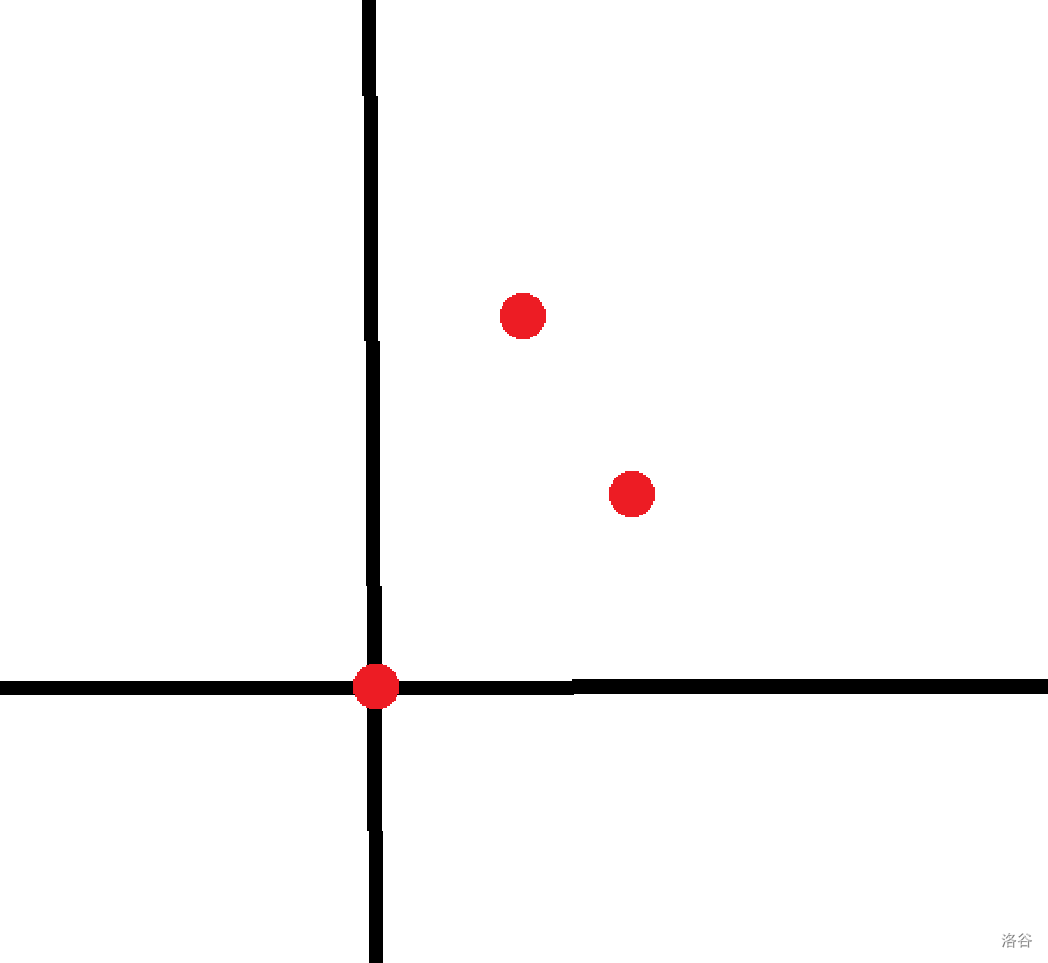
只要它的剩下一个点在第一个点右上方并且不与这两个红点重复，就直接把答案 −1-1。
此时应该使答案 +1+1 的实际上会使答案 +1+1，使答案 −1-1 的实际上会使答案 −3-3，可以对于每一个这样的东西，都将答案 +1+1。
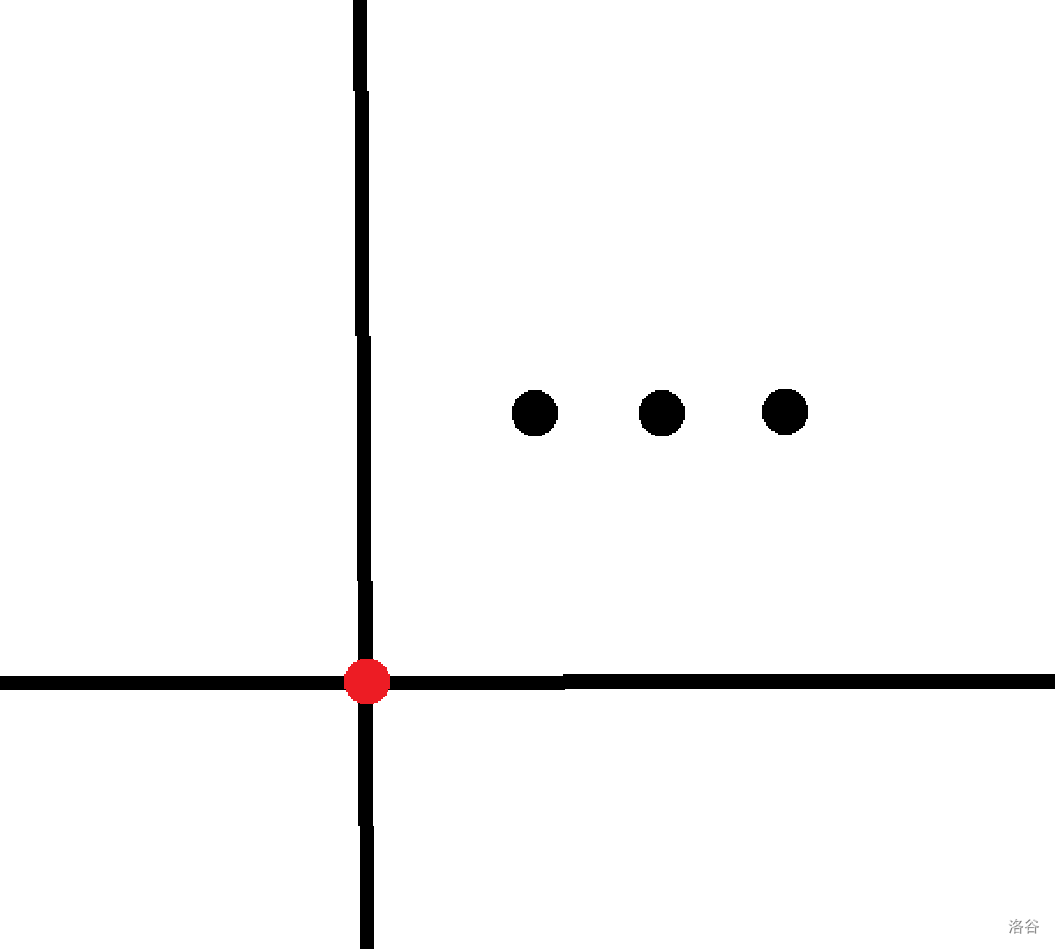
然后就可以考虑对于第一个点右上方三个点的每一种排列，对答案的贡献是多少。
这种情况贡献是 1+1+1=31+1+1=3，3+1=43+1=4。
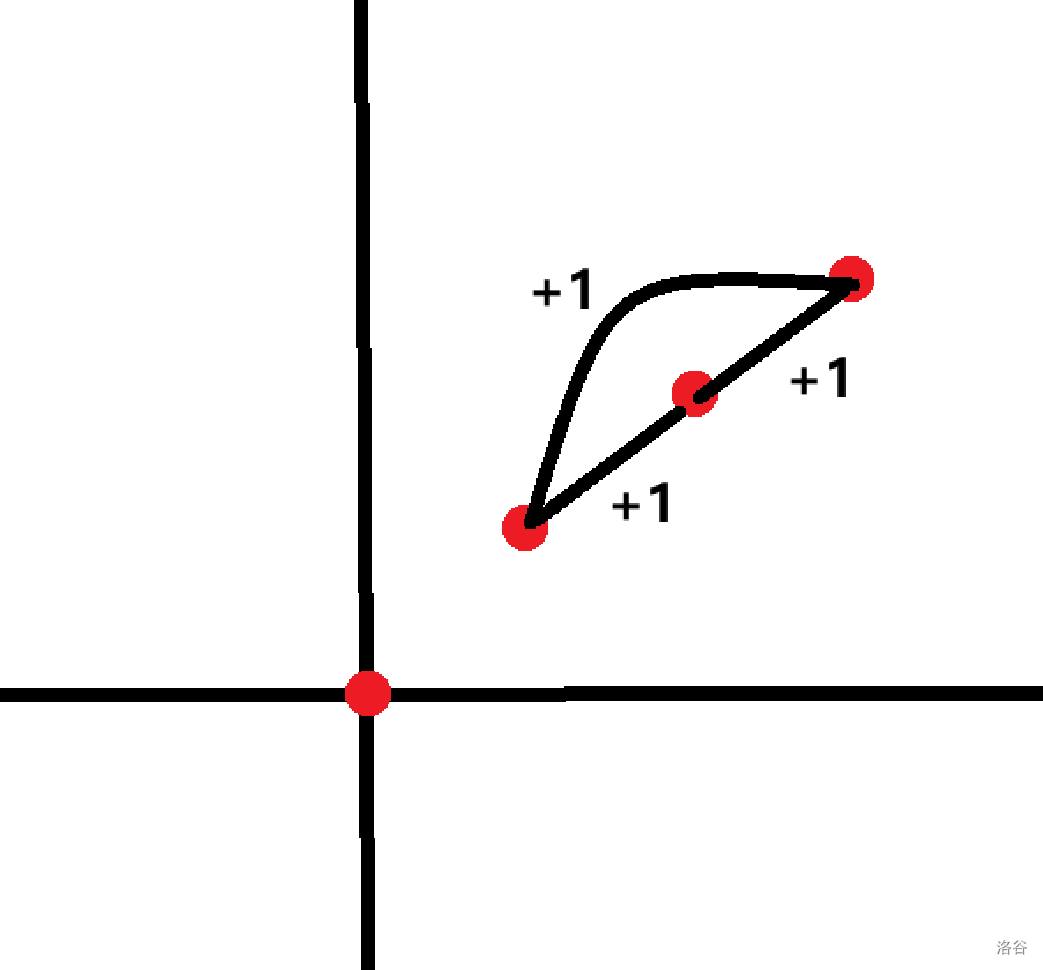
这种情况贡献是 1+1−1=11+1-1=1，1+1=21+1=2。
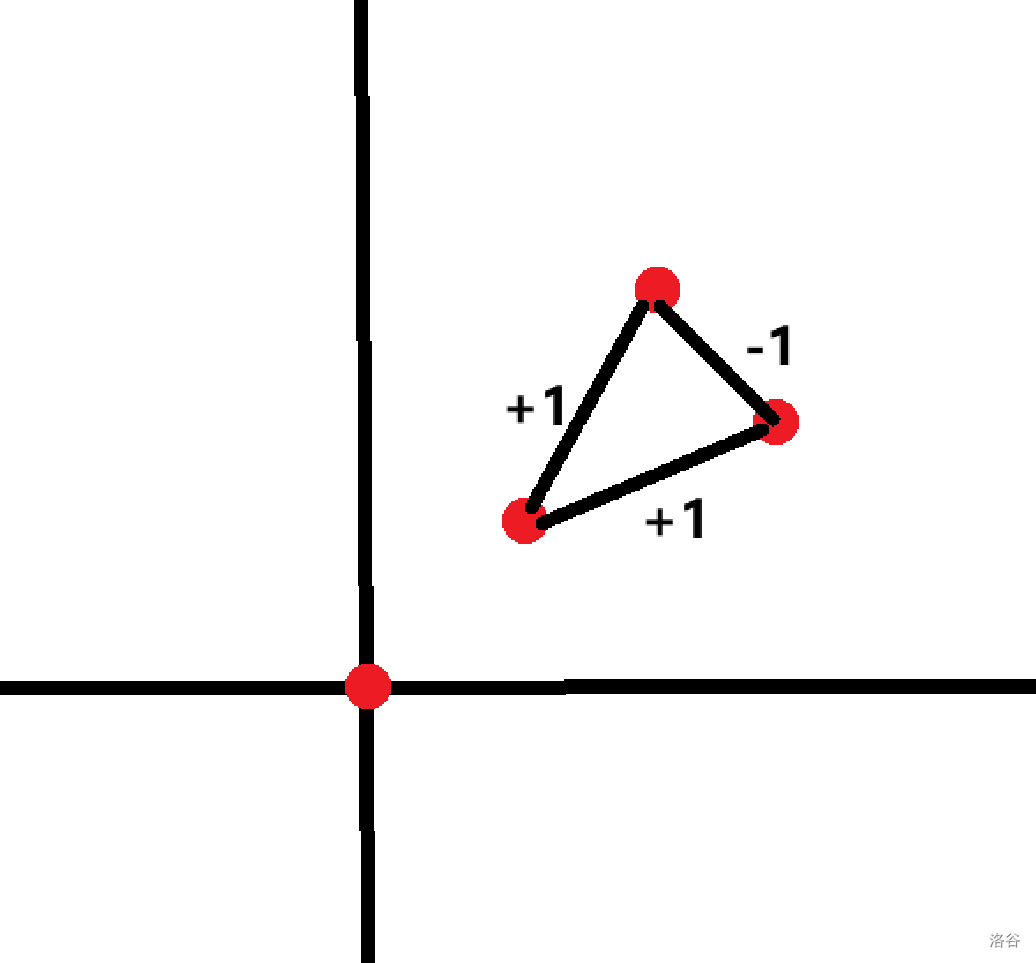
这种情况贡献是 1+1−1=11+1-1=1，1+1=21+1=2。
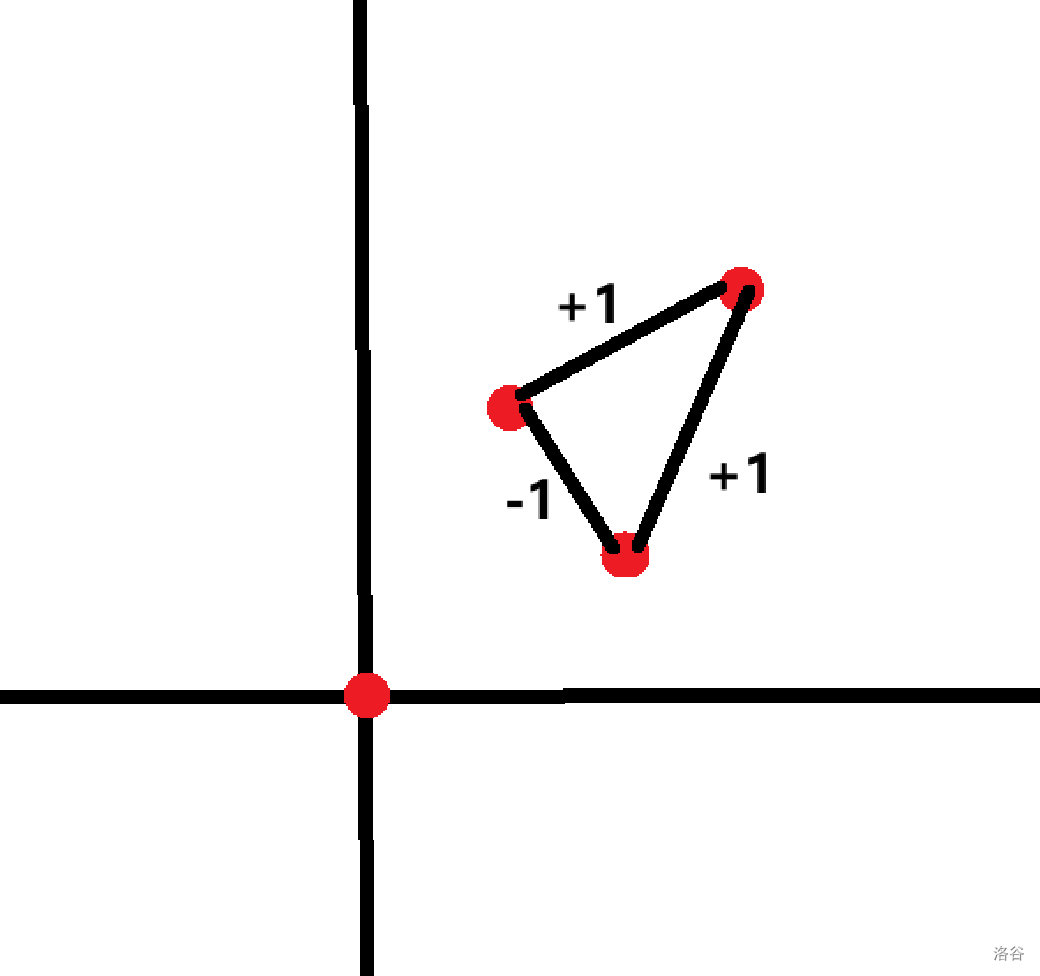
这种情况贡献是 1−1−1=−11-1-1=-1，−1+1=0-1+1=0。
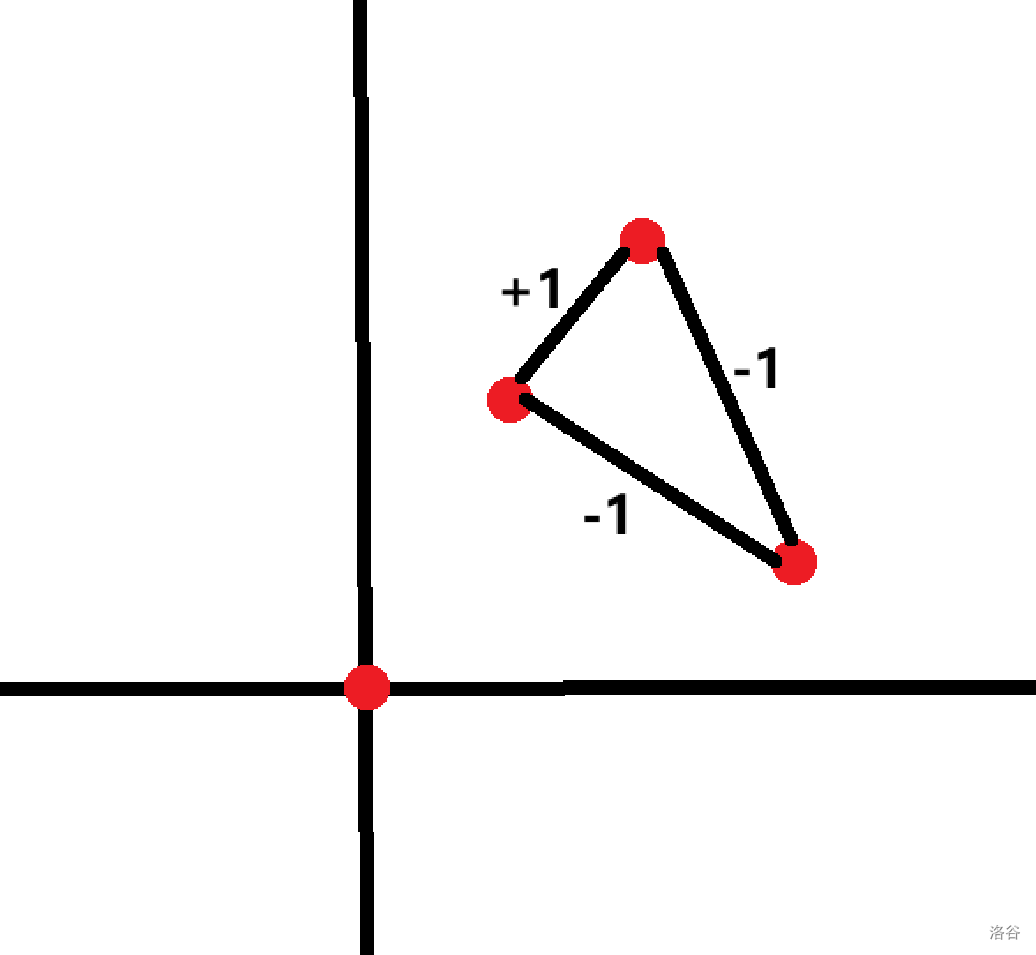
这种情况贡献是 1−1−1=−11-1-1=-1，−1+1=0-1+1=0。
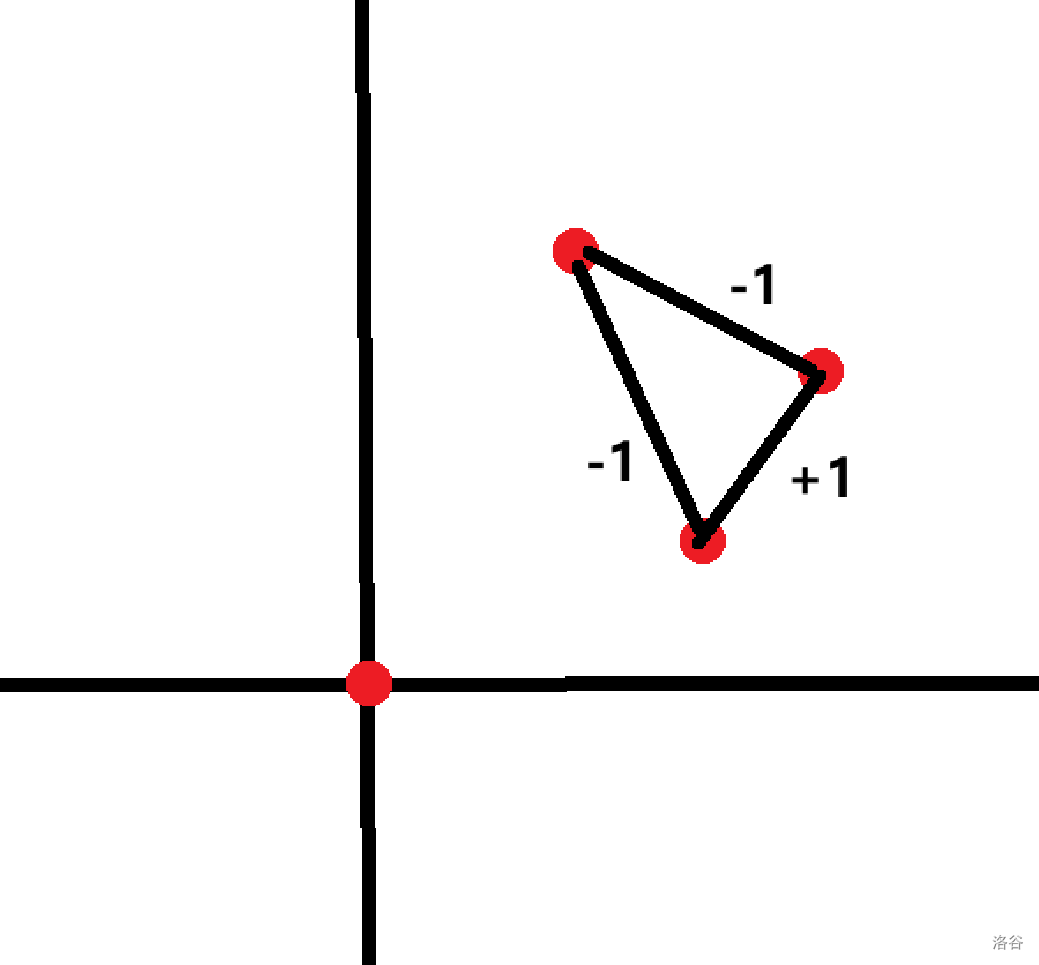
这种情况贡献是 −1−1−1=−3-1-1-1=-3，−3+1=−2-3+1=-2。
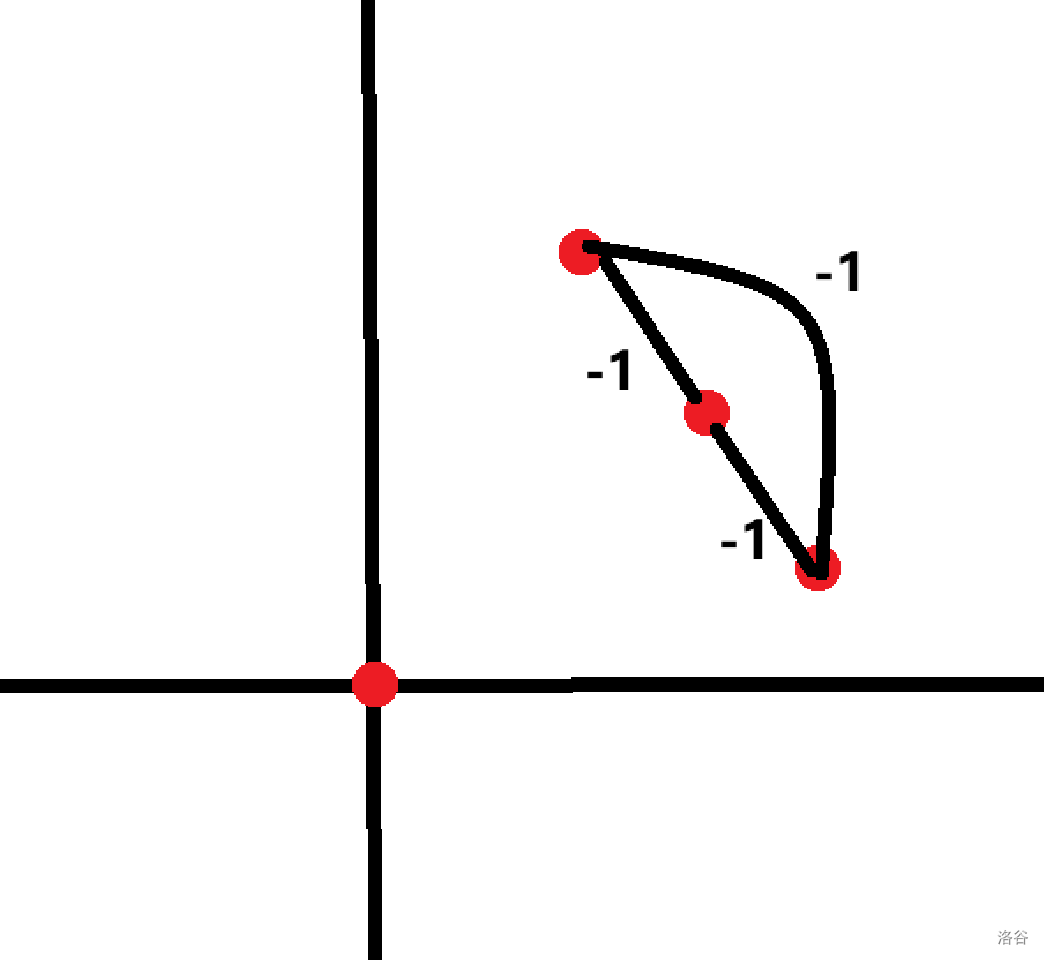
发现除了我们要算入答案的情况 33 和情况 66，剩下的，刚好是我们刚才算的情况 11 和情况 22，以及对答案没有影响的情况 44 和情况 55。
非常妙的一题，出题人巧妙地用了 AA 类山峰图腾来给最后答案的计算做铺垫，并且使最后的答案不能算的部分的贡献恰好为 00，给出题人点了。
然后这道题到这里就做完了，只需要跑三遍扫描线，代码也是不难的。
这里贴上代码
CPP
#include<bits/stdc++.h>
#define pii pair<long long,long long>
#define mp make_pair
#define pb push_back
using namespace std;
unsigned int n,a[200005],b[200005],d[200005],ans=0,sum=0,ans1=0,ans2=0;
struct szsz {
	unsigned int v[200005];
	inline void change(int wz,unsigned x) {
		for(; wz<=n; wz+=wz&-wz)v[wz]+=x;
	}
	inline unsigned int check(int wz,unsigned int res=0) {
		for(; wz; wz-=wz&-wz)res+=v[wz];
		return res;
	}
};
szsz c,c1,c2;
int main() {
//	freopen("d.in","r",stdin);
//	freopen("d.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=1; i<=n; i++) {
		cin>>a[i];
		d[i]=c2.check(a[i]);
		c2.change(a[i],1);
	}
	for(int i=n; i>=1; i--) {
		b[i]=(n-i)-c.check(a[i]);
		unsigned int t=sum-c1.check(a[i]);
		ans+=(__int128)b[i]*(b[i]-1)*(b[i]-2)/6;
		if(b[i]>2) {
			ans+=2*t*(b[i]-2);
			ans-=b[i]*(b[i]-1)/2*(b[i]-2);
		}
		ans1+=t*d[i];
		ans2+=b[i]*(b[i]-1)/2*d[i];
		sum+=b[i];
		c1.change(a[i],b[i]);
		c.change(a[i],1);
	}
//	cout<<ans1<<" "<<ans2<<"???\n";
	ans2-=ans1;
	ans-=4*ans1;
	ans-=2*ans2;
	ans>>=1;
	ans-=ans2;
	cout<<ans%(1<<24);
	return 0;
}

评论

共 12 条评论，欢迎与作者交流。

正在加载评论...