专栏文章

线性求最小生成树算法学习笔记

cc_legg
算法·理论参与者 3已保存评论 3

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
3 条
当前快照
1 份
快照标识符
@miof2pbj
此快照首次捕获于
2025/12/02 18:10
3 个月前
此快照最后确认于
2025/12/02 18:10
3 个月前
查看原文

前言

神秘的算法，又是 Tarjan 的作品。

介绍

在这里，可以找到这个算法的名字：Karger-Klein-Tarjan 算法，然后在这里（这么抽象的东西居然是卡内基梅隆大学的课件？）有该算法的简写：KKT 算法。
注意 KKT（Karger-Klein-Tarjan）算法不是 KKT（Karush-Kuhn-Tucker）条件。
该算法基于 Boruvka 算法，Boruvka 算法的时间复杂度是 Θ(mlog⁡n)\Theta(m\log n)，而 KKT 算法的期望时间复杂度为 Θ(m)\Theta(m)，最坏时间复杂度为 Ω(min⁡{n2,mlog⁡n})\Omega(\min\{n^2, m\log n\})。

Boruvka 算法

要学会 KKT，我们要先学会 Boruvka 算法，而 Boruvka 算法是由 Boruvka step 组成的。每个 Boruvka step 的时间复杂度是 Θ(m)\Theta(m)，它可以求出一个带权连通图的最小生成森林。

最小生成森林

一个带权连通图的最小生成森林是该图的一个子图（包含原图中所有点，但不一定包含所有边），可以不连通，当然还有一些其他性质。
但在这个算法里，最小生成森林的用处就在于：一个带权连通图的最小生成森林也是该图的最小生成树的一个子图。
然后我们还有另一个贪心的性质：对于一个结点，连接它的边中权值最小的边一定在最小生成树上（所以也可以在最小生成森林上）。
所以我们就知道怎么进行 Boruvka step 了：
对每个结点，找到连接它的边中权值最小的边，然后把它加入一个边集里。根据上面的性质，把不在这个边集里的边去掉，得到的图就是原图的一个最小生成森林。
例如（加粗的边是一次 Boruvka step 之后会选出的边）：
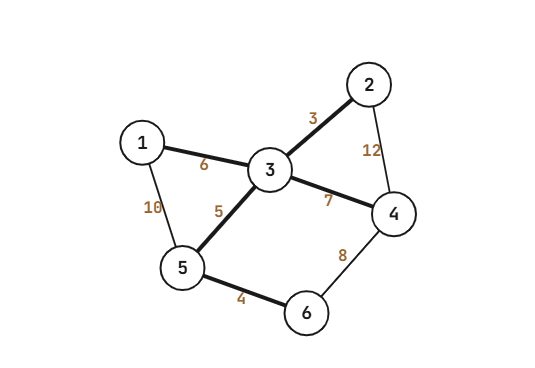
然后我们可以来看 Boruvka 算法，它的步骤如下（假设原图为 GG）：
  1. 对 GG 进行一次 Boruvka step；
  2. 得到的图中可能会有很多连通块，我们把每个联通块缩成一个点，并保留每个连通块间的边，这会得到一个新图 G1G_1；
  3. 如果 G1G_1 中只有一个结点，那么 Boruvka 算法结束，否则回到步骤 1 对 G1G_1 进行同样的事情。
非常简单的算法。
然后我们可以来进行一下复杂度分析：
  • 显然一次 Boruvka step 的时间复杂度是 Θ(m)\Theta(m)；
  • Boruvka 算法的时间复杂度取决于执行 Boruvka step 的次数，所以它的复杂度为 Θ(mx)\Theta(mx)，xx 是执行 Boruvka step 的次数；
  • 又每次执行 Boruvka step 后节点数至少减半，所以执行次数 x=log⁡nx=\log n；
  • 综上 Boruvka 算法的时间复杂度为 O(mlog⁡n)O(m\log n)，最坏是 Ω(min⁡{n2,mlog⁡n})\Omega(\min\{n^2, m\log n\})，最好是 Ω(m)\Omega(m)。

KKT 算法

所以讲了那么多，还没开始讲 KKT？
下面我们来介绍线性求最小生成树地算法。
首先我们还要引入一个叫 FF 重/轻边的概念。
假设原图 GG 上有一条边 (u,v)(u, v)，权值为 ww，然后在 GG 的最小生成森林中连接 uu 和 vv 的路径中的权值最大的边的权值为 wFw_F（如果在 FF 中 uu 和 vv 不在一个连通块里就令 wF=∞w_F=\infin）。
如果 w≤wFw\le w_F，边 (u,v)(u, v) 就是一条 FF 轻边，反之就是 FF 重边。
然后我们再不加证明的写下两个引理：
  1. 对于上面定义的 GG 和 FF，所有 FF 重边不在 GG 的最小生成树中。
  2. 若 HH 是 GG 的一个子图，且 HH 包含 GG 中每条边的概率都为 pp，然后 FF 是 HH 的一个最小生成森林，则在 GG 中，FF 轻边的期望数量最多为 np\frac{n}{p}。
于是就有了 KKT，算法步骤如下：
  1. 对 GG 做两次 Boruvka step，节点数变为 n4\frac{n}{4}，设这个收缩了的图为 G1G_1，如果 G1G_1 中只有一个结点，那么算法结束；
  2. 构造出 G1G_1 的子图 HH 使得 HH 包含 G1G_1 中每条边的概率都为 12\frac{1}{2}，然后求出 HH 的一个最小生成森林 FF，再删除 G1G_1 中的所有 FF 重边得到子图 G2G_2；
  3. 对 G2G_2 做同样的事。
然后 KKT 算法就结束了，我们来算一下它的复杂度。
设对于一个 nn 个结点，mm 条边的图，KKT 的期望操作次数为 T(n,m)T(n, m)，那么有：
T(n,m)≤c(m+n)+T(n4,m2)+T(n4,n4)T(n, m)\le c(m+n)+T(\frac{n}{4}, \frac{m}{2})+T(\frac{n}{4}, \frac{n}{4})
其中 cc 是一个适当的常数，不等式可以用上面的引理二来解释。
以及可以用归纳法证明 T(n,m)=Θ(m)T(n, m)=\Theta(m)，易证从略。

参考文献/撒花

A randomized linear-time algorithm to find minimum spanning trees
Karger-Klein-Tarjan 演算法 - 演算法的分析與證明
期望线性复杂度最小生成树算法学习笔记 - 洛谷专栏
theory_lunch_presentation_KKT.pdf
最小生成树 - OI Wiki
R. C. T. Lee, S. S. Tseng, R. C. Chang, Y. T. Tsai. 算法设计与分析导论[M]. 北京：机械工业出版社，2008.

评论

共 3 条评论，欢迎与作者交流。

正在加载评论...