题解：CF1528F AmShZ Farm

首先我们尝试解决关于序列 $a$ 的计数问题，我们先记 $a$ 的桶 $c_i=\sum_j[a_j=i]$，则 $c$ 需要满足 $\sum_{j=1}^ic_j\geq i$，考虑使用组合意义求出 $a$ 的数量：

我们构造一个根节点为 $1$ 的，大小为 $n+1$ 的有根树，随后我们对这个树进行 dfs，在每一个节点时按照其儿子节点的编号顺序访问，dfs 的同时记录下每一个节点的儿子数量。

根据序列我们可以根据记录的儿子数量反向推导出树的形态（儿子有顺序），之后我们可以直接令根节点为 $1$，将 $2\sim n+1$ 这些编号填入其他节点，但是由于 dfs 时有儿子节点的编号顺序，实际上方案数为 $\frac{n!}{\prod_ic_i!}$。

而我们发现 $c$ 的合法条件与序列可以重构出树的合法条件是一致的，因此实际上根节点为 $1$ 的，大小为 $n+1$ 的有根树个数就直接等于 $a$ 序列的个数，也就是 $(n+1)^{n-1}$。

接下来我们考虑原问题，我们记 $c$ 数组为这棵树每个节点的儿子个数，也就是对于每个树加上 $\sum_{i}c_i^k$ 的权值。

首先斯特林一下，我们先求权值为 $\sum_{i}c_i^{\underline{k}}$ 的问题。为了方便我们将这棵树视为根节点任意的有根树，最后将答案除以 $n+1$ 即可。

考虑组合意义即为，枚举有根树，然后枚举有根树上的一个节点，然后有序枚举 $k$ 次这个节点的儿子子树，并将其割掉，的方案数。

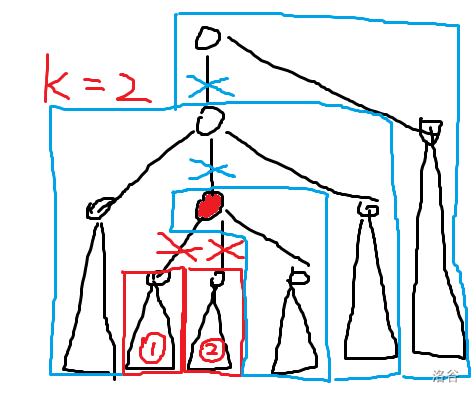
不妨考虑如图所示的分割方案，下面两个红色的断边为组合意义中顺序枚举 $k$ 次断边，而上面蓝色的断边则是断开了枚举的节点与根节点之间的路径，这些操作会使得该图出现恰好 $k$ 个红色有根树与至少一个蓝色有根树。

不妨直接枚举这至少 $k+1$ 个有根树，并且钦定顺序后将后 $k$ 个有根树标记为红色，其余标记为蓝色。对于蓝色有根树，将其根节点连接到上一个蓝色有根树的根节点上，对于红色有根树，将其根节点连接到最后一个蓝色有根树的根节点上，即可使用这些零散的有根树还原出原本的有根树，顺便把组合意义算上了。

因此我们实际上需要统计的是，$n+1$ 个有标号节点组成了至少 $k+1$ 个有序的有根树的方案数，这个可以使用 prufer 序列计数，问题转换为，你有 $0\sim n+1$ 这些节点，节点 $0$ 的度数应当大于等于 $k+1$，并且节点 $0$ 的儿子有序的方案数，进而转化为，你有一个长度为 $n$ 的序列，你可以在序列中填入 $0\sim n+1$ 的数，要求 $0$ 的个数大于等于 $k$ 个并且假设出现 $x$ 个 $0$ 则贡献为 $(x+1)!$。

考虑组合意义，我们不妨在 prufer 序列的末尾添加一个 $0$，我们从这个特殊的 $0$ 出发，尝试依次在其余的 $0$ 之间游走，走到最后一个 $0$ 的时候可以指向任意一个 $0$，这样构造出来的方案数刚好为 $0$ 的个数的阶乘。另一边，考虑一张 $n+1$ 个点的基环树森林，我们从节点 $n+1$ 出发，往前走出一个 $\rho$ 形，将所有访问过的点修改为 $0$，我们就可以发现这两个模型是形成双射的，因此当不限制 $0$ 的个数时我们的方案数为 $(n+1)^{n+1}$。

重新考虑 $0$ 的个数，相当于在 $0$ 之间游走的前 $k$ 步，我们必须扩展出新的节点，这个可以通过将上面的答案加入下降幂得到，答案为 $(n+1)^{n+1-k}n^{\underline{k}}$。当然最后我们要把有根转回无根：$(n+1)^{n-k}n^{\underline k}$。

最后我们使用公式：

将式子代入得到最终答案：

写一个第二类斯特林数·行就做完了！